이전에 구체 구현을 정리하며 썼던 게시물과 상당히 유사한데, 이 게시물에서 많은 부분을 참고했기 때문이다.
2차원 상의 원의 방정식
이해를 위해 3차원이 아닌 2차원 상의 좌표 평면을 상상해보자.
좌표 평면 상에서 원의 방정식을 나타내면 다음과 같다.
원의 중심이 원점(0, 0)인 원이 있다고 가정할 때 x, y가 의미하는 것은 구위(원의 테두리)의 좌표이며 r은 해당 원의 반지름이 된다.
(-y, x)는 오타다! → (x, -y)
좌표를 어디에 찍든 해당 공식은 성립하는데, 어느 테두리에서든 수직으로 발을 내리면 직각 삼각형이 생겨나고, 해당 삼각형의 빗면이 원의 반지름이 되기에 피타고라스의 정리를 통해 반지름을 구할 수 있기 때문이다.
원의 중심이 이동한 원의 방정식
// object_create.c
struct t_point3
{
double x;
double y;
double z;
};
t_sphere sphere(t_point3 center, double radius)
{
t_sphere sp;
sp.center = center;
sp.radius = radius;
sp.radius2 = radius * radius;
return (sp);
}
// main.c
t_sphere sp;
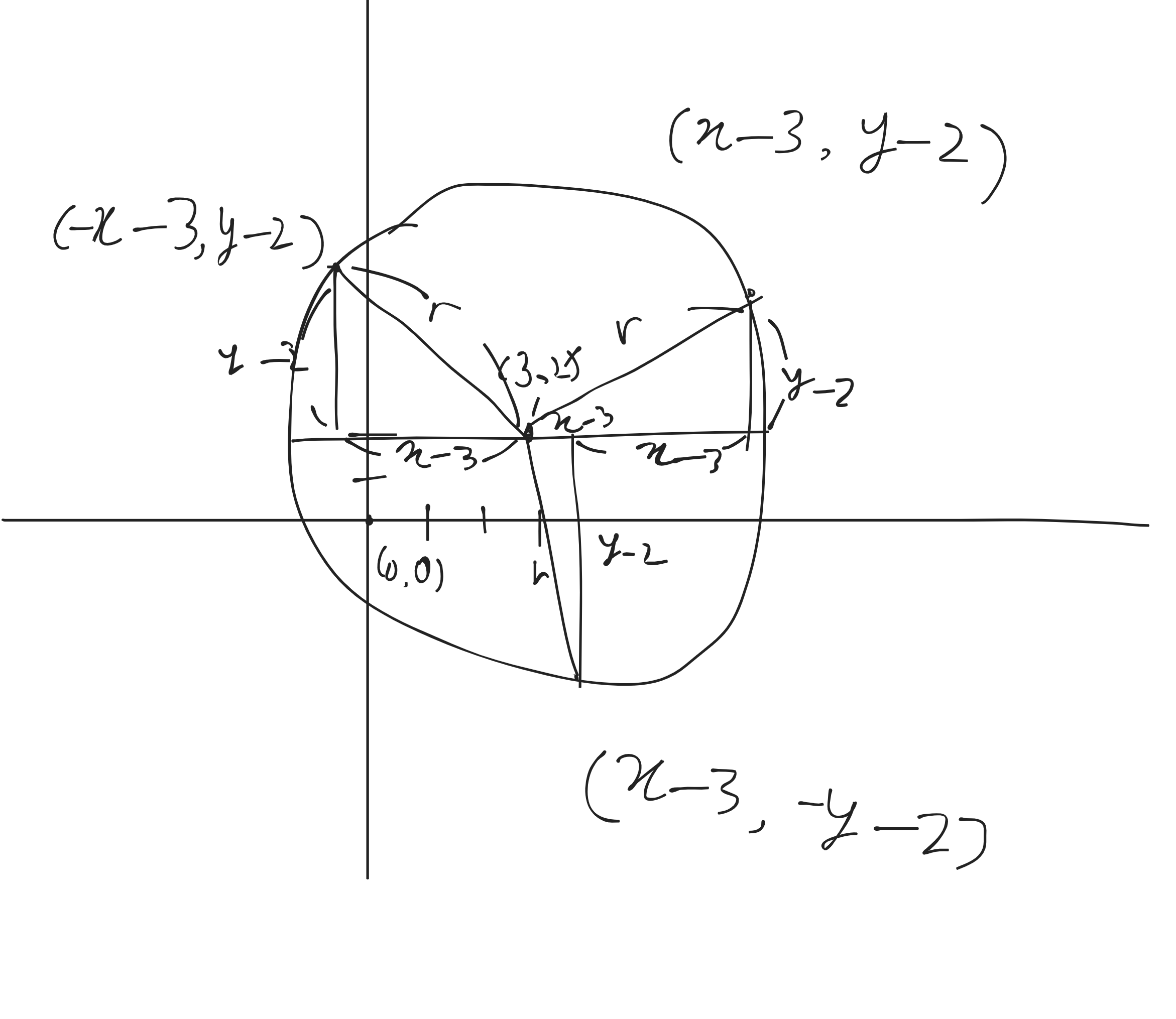
sp = sphere(point3(-4, -8, -30), 20);우리가 실제로 원을 배치할 때는 3차원 좌표의 원점에서부터 떨어진 위치에 배치를 하게 되는데, 이 때 원의 중심점은 벡터 구조체로 표현하고 있지만 의미하는 것은 원점으로부터 얼마나 떨어져 있는 지를 의미한다.
실제 원의 좌표, 원의 중점이 (3, 2)라고 했을 때, 원의 구위의 좌표 값을 이동한 만큼 빼주어야 반지름의 값이 제대로 나올 수 있다.
원의 중심을 의미하는 좌표를 C라고 했을 때 이를 식으로 표현하면 다음과 같이 표현할 수 있다.
이 때 x, y의 좌표는 원의 구위를 의미한다.
백터로 표현할 경우
좌표 평면의 특정 점을 우리는 벡터로 표현할 수도 있을 것이다.
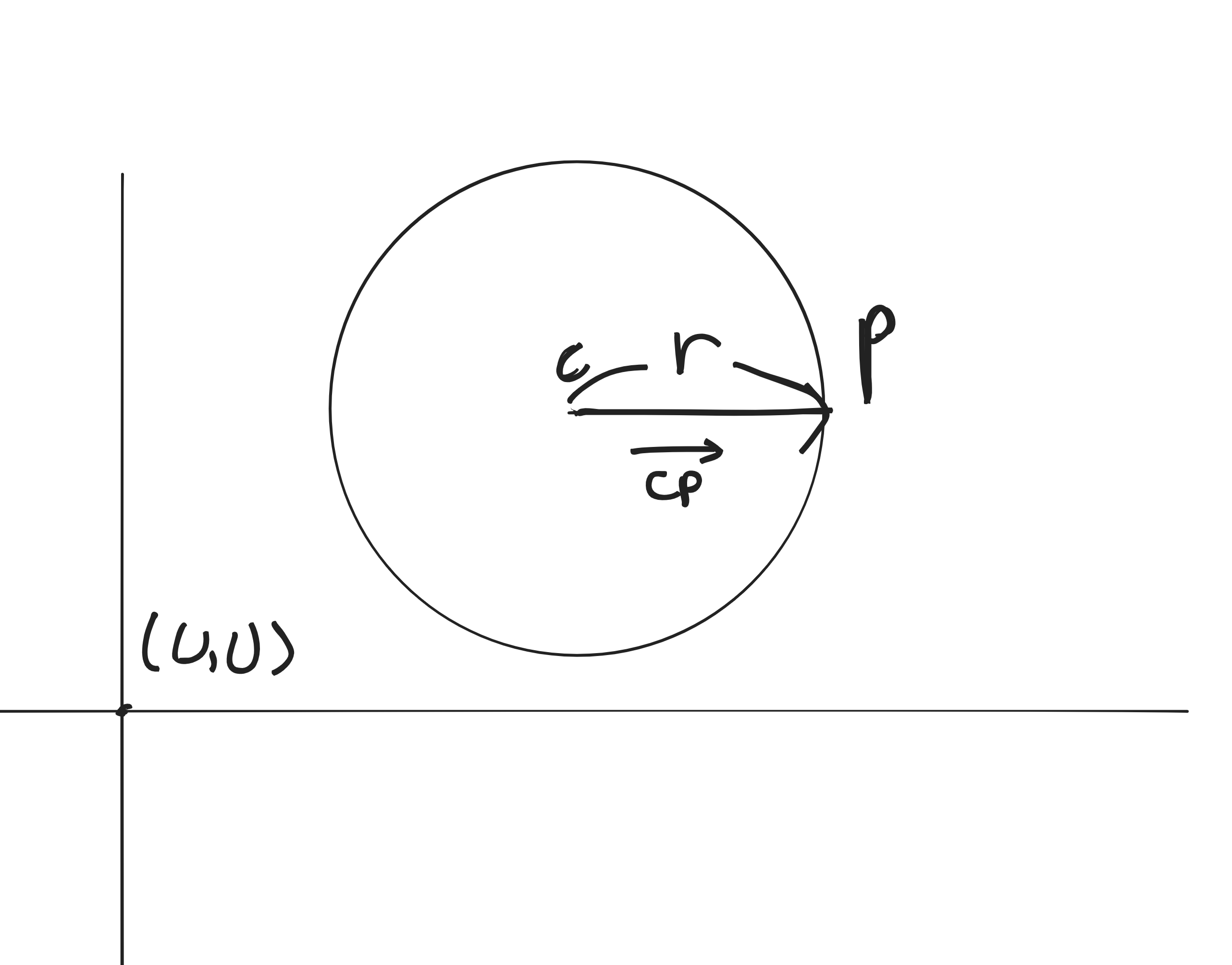
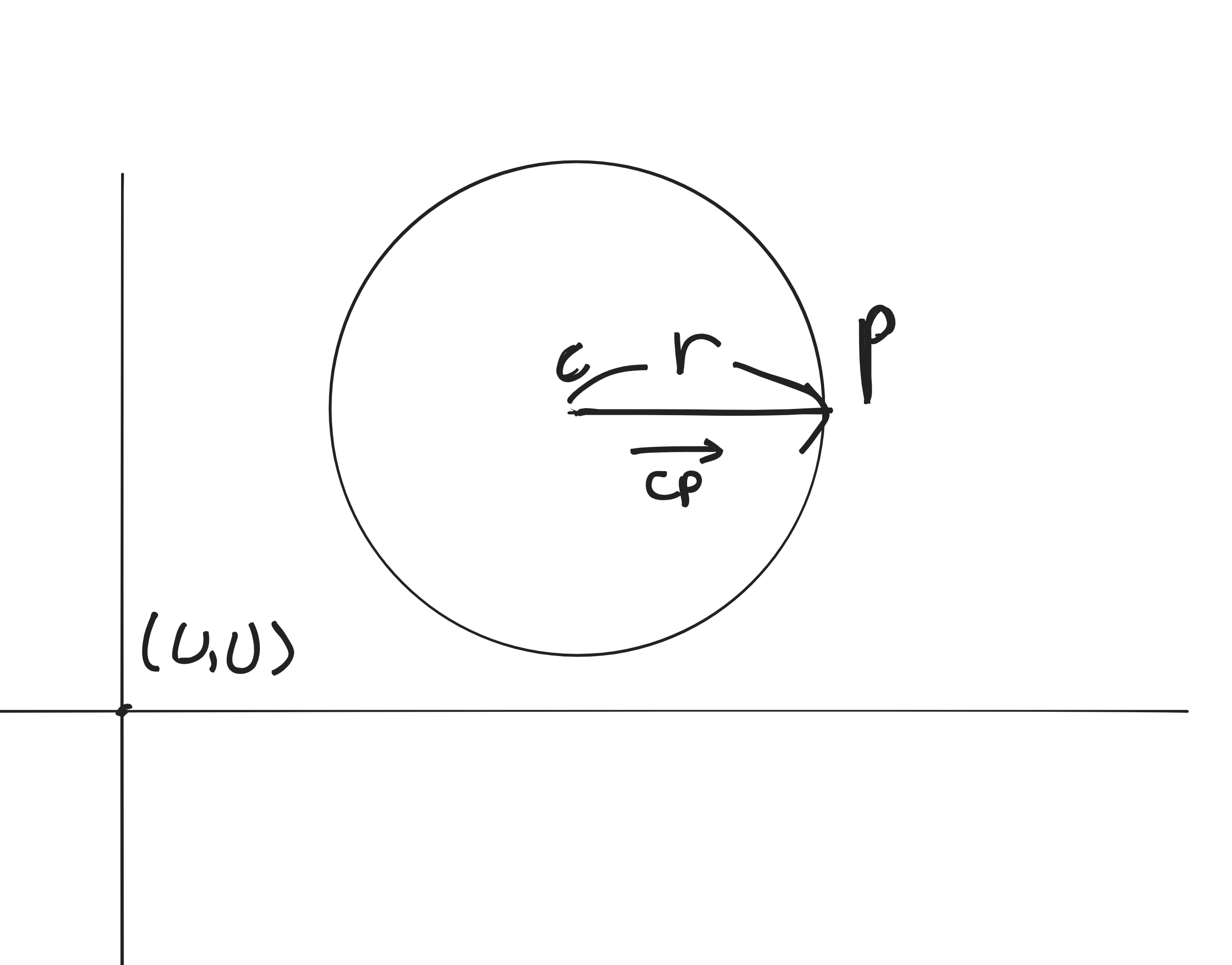
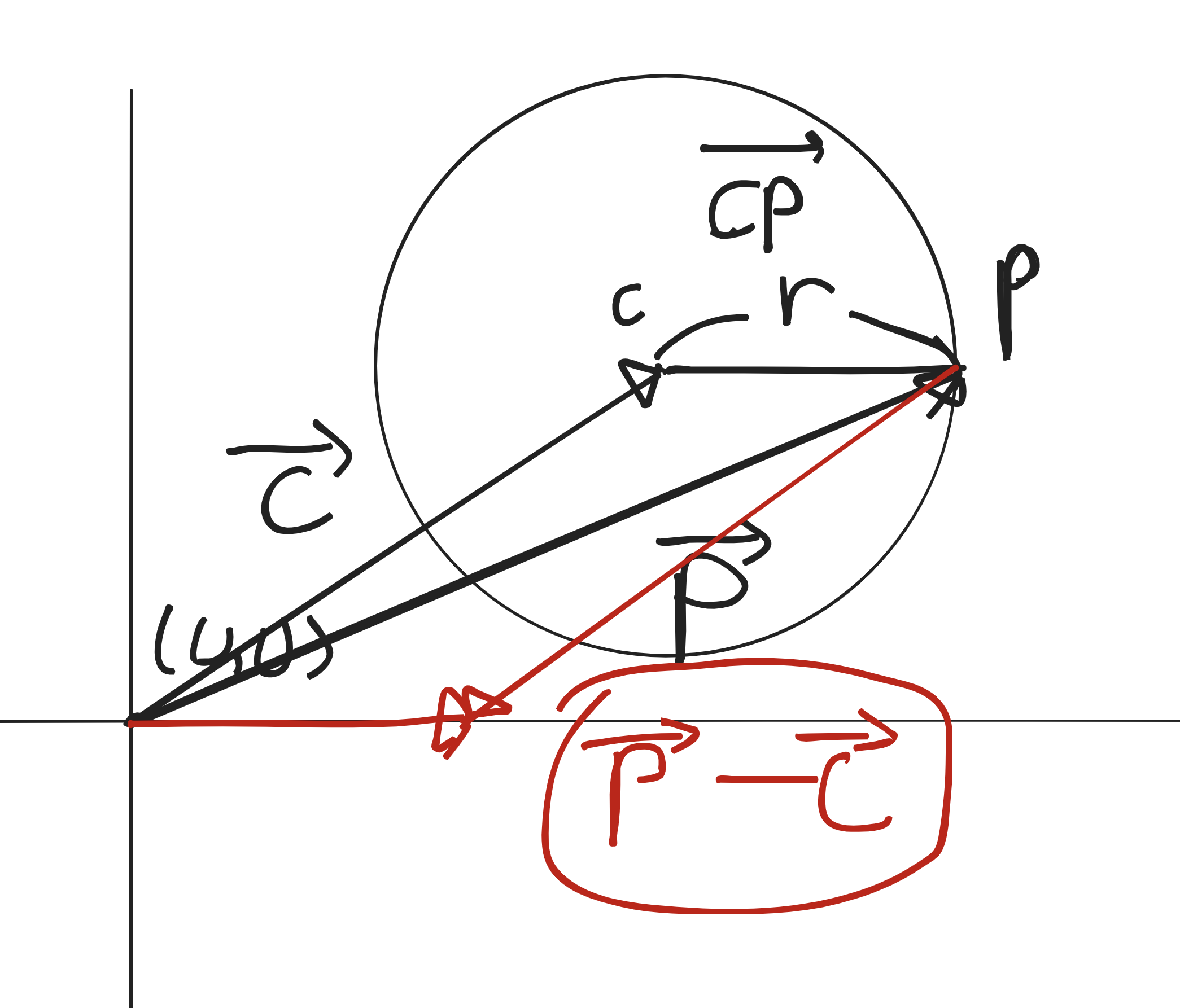
원의 중심을 C라고 하고 원의 구위를 P라고 한다면 원의 반지름 r을 다음과 같이 표현할 수 있으며, 그림으로는 다음과 같다.
|백터|의 의미는 벡터의 길이(스칼라) 값을 의미한 것이다.
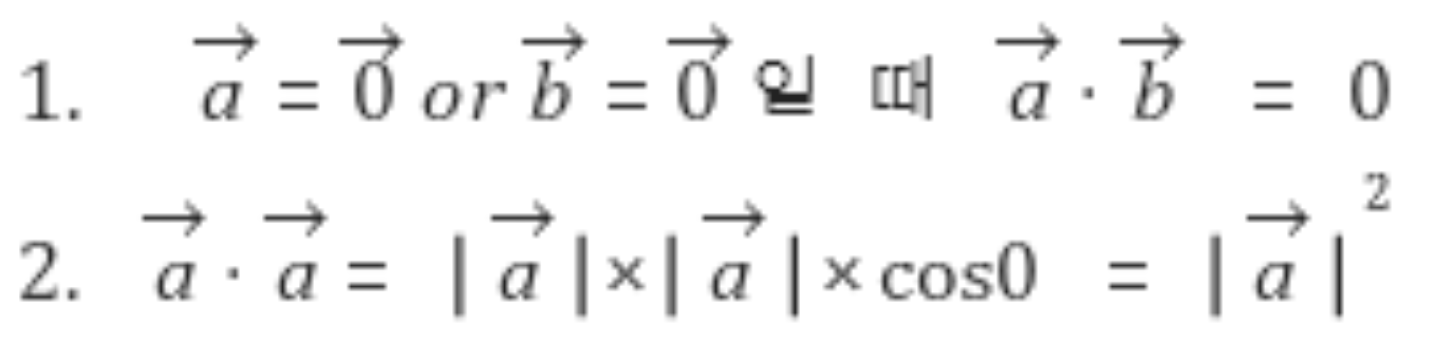
이 때 양변을 제곱해준 후, 좌변을 내적으로 표현하게 되면 다음과 같은 식이 성립한다.
내적의 특징
백터의 길이의 제곱이 어떻게 해서 백터를 내적한 것과 동일한지 이해가 가지 않았는데, 이는 내적의 특징 때문이었다.
https://t1.daumcdn.net/cfile/tistory/99450C335A17C3B036
https://t1.daumcdn.net/cfile/tistory/99CE07335A17C55C12
내적의 특징 중 동일한 벡터가 있을 경우에는 두 벡터가 이루는 각은 0도이므로 cos0 = 1이 되는 특징이 있었다. 그러므로 벡터 a의 절대값(길이)의 제곱이 되는것을 알 수 있다.
중심 C, 구위 P를 백터로 치환

두 점 C, P가 다른데도 불구하고 어떻게 동일한 (백터 P - 백터 C)로 표현할 수 있는지 이해할 수 없었는데, 그림으로 그려가며 따라하니 겨우 이해 할 수 있었다.
각각의 점은 다음과 같은 백터로 표현할 수 있다.
백터의 뺄셈이라고 하면 A벡터 + (-B)벡터(역백터)와 같다.
백터 P에서 백터 C를 뺀다고 했을 때, 백터 P의 종점에서 백터 C의 시작점을 두고 반대 방향으로 뻗어나가게 된다.
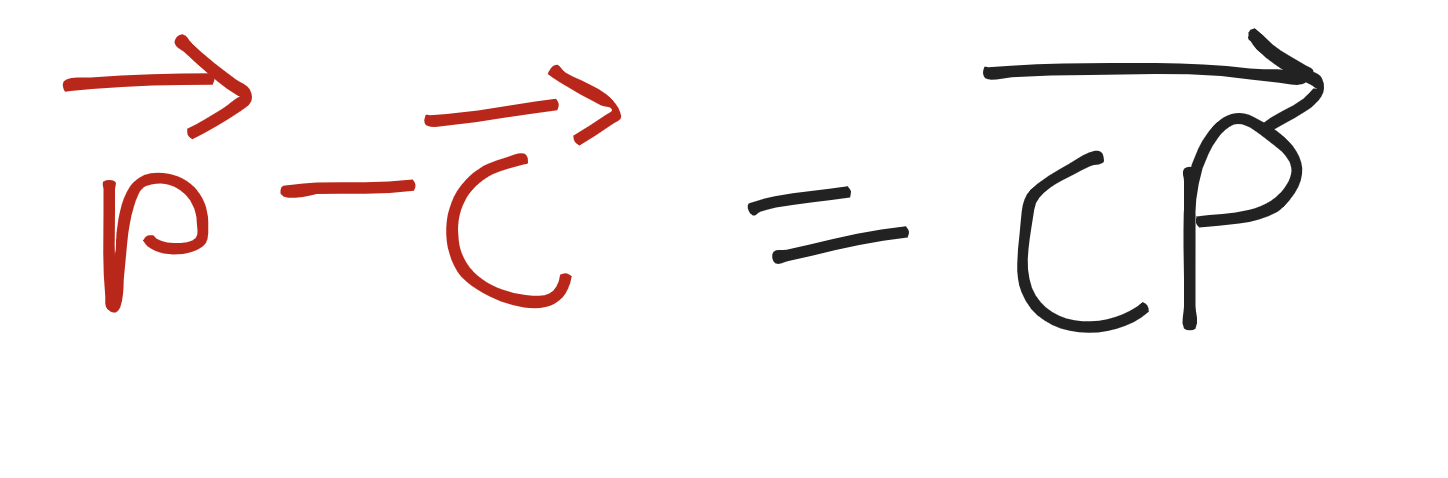
백터의 뺀 결과 역시 백터로 나타내었을 때 크기와 방향이 똑같아지는데, 두 백터가 크기, 방향이 동일할 경우 위치에 상관없이 같은 백터가 된다.
즉 다음과 같은 식이 성립할 수 있는 것이다.
이제 우리는 광선을 쏘았을 때 해당 광선이 원의 구위에 충돌했다고 가정함으로써 백터 P를 광선을 쏘았을 때의 방정식으로 치환시켜볼 것이다.
광선을 쏘게 되었을 때
광선(레이)의 방정식
다음 식은 실제 레이를 쏘았을 때의 식이다.
O - 원점 좌표
- 광선를 쏘는 시작점이다.
- (0, 0, 0)
D - 방향벡터
- 단위 백터, 벡터가 향하는 방향이다.
t - 벡터의 크기(길이)
- 스칼라, 1을 기준으로 표준화를 해주었기에 얼마나 걸리는 지 알 수 없다.
광선이 부딪힐 경우
방향벡터 방향으로 광선을 쏘았을 때, 이때 좌표상의 구에 우리가 쏜 광선과 부딪힌 지점이 존재할 경우 해당 점이 곧 원의 구위, 백터 P가 되고 t의 값은 바로 부딪힌 지점과 정점 A사이의 크기가 된다.
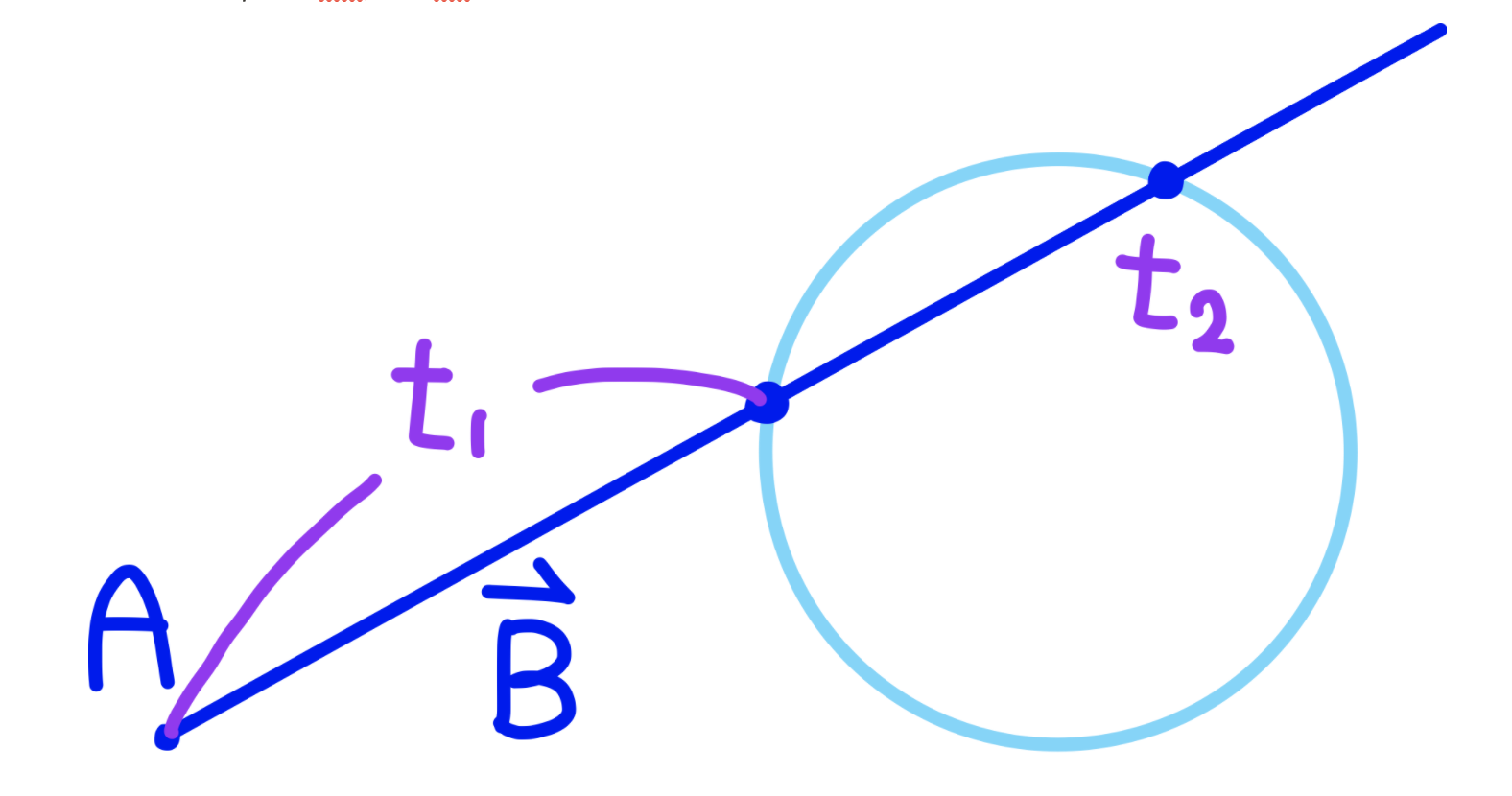
이 때 벡터 P를 P(t)로 치환시켜도 아무런 문제가 없을 것이다. 거리를 모르더라도 단위 백터를 알고 있으니 같은 방향으로 계속 나가게 되면 부딪힐 광선은 부딪힐 것이기 때문이다.
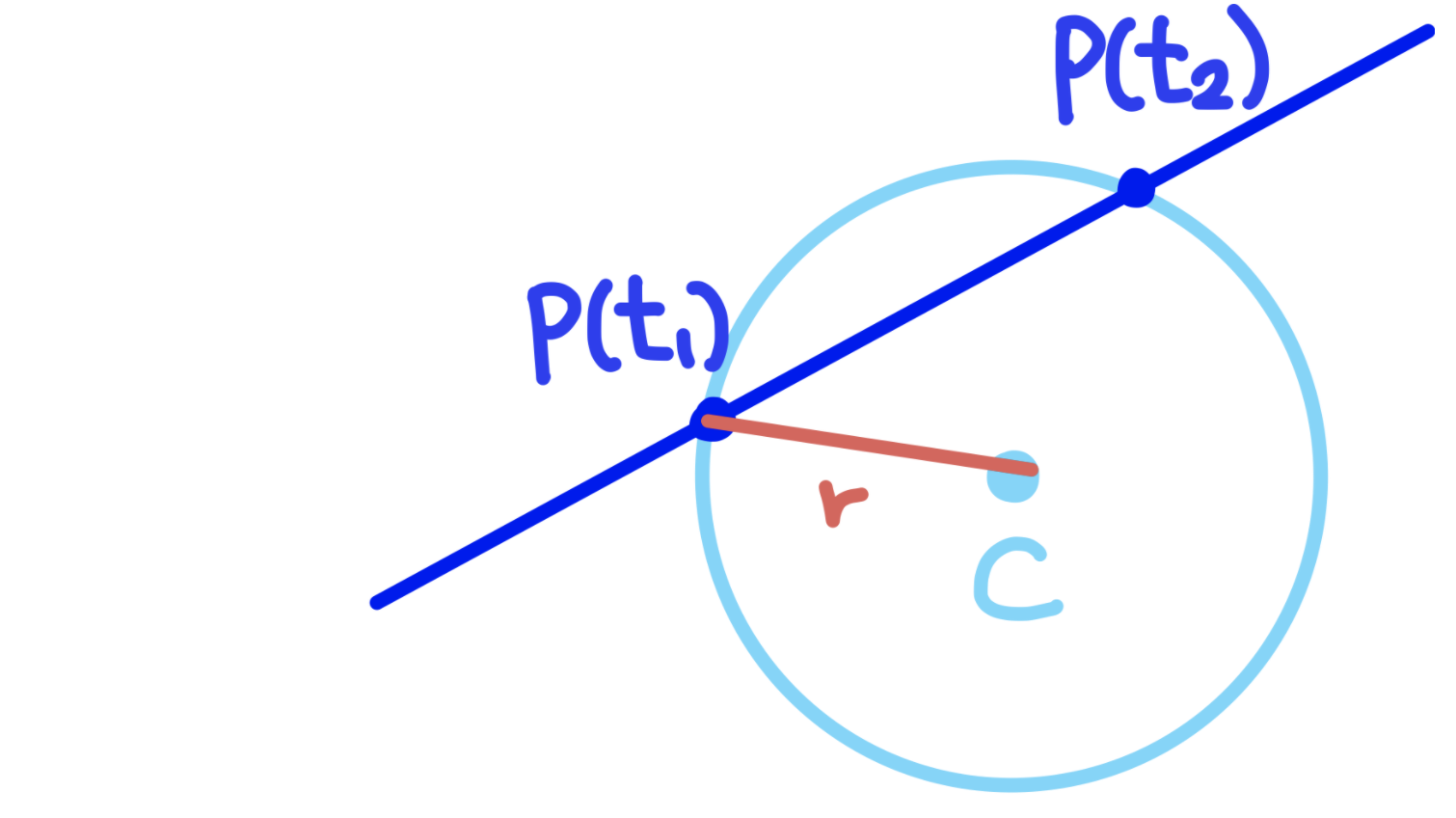
이 식의 결과로 해가 존재한다면 우리가 쏜 ray가 구 위에 있다는 것을 알 수 있게 된다.
즉 위에서 전개했던 백터 P는 우리가 실제로 쏘게 되는 레이의 방정식과 대응하게 되는 것이다.
위 식을 전개하면 아래와 같아진다.
다시 한 번 짚고 넘어가보자.
O - 백터의 원점, 광선이 출발한 지점
D - 광선의 단위백터, 0 ~ 1의 범위 내 값이다.
t - 백터의 길이, 1로 표준화한 단위 벡터이기에 값이 얼마인지는 아직 알 수 없다.
C - 원의 중심점, 백터가 아닌 3차원 공간 내에서의 좌표다. 원점에서 얼마나 떨어져 있는지를 담는다.
r - 원의 반지름.
우리는 카메라의 위치는 A(정점좌표)를 알고 있고, ray를 쏘는 방향 b(방향벡터)를 알고 있다. 그리고 구 중앙의 정점좌표인 C와 구의 직경인 r을 모두 알고있다.
따라서 우리가 모르는 변수는 t이고 t에 대한 식으로 위의 식을 정리해보면 아래와 같은 수식이 나온다.
우리가 구해야 하는 값은 t값이다. 2차방정식의 해를 구하기 위해 근의 공식을 사용해 줄 수 있다. 근의 공식으로 위의 수식을 풀면 다음과 같은 꼴의 수식이 된다.
이 때 t(x)에 대한 이차항, 일차항, 상수항은 다음과 같다.
이것을 우리가 잘 아는 근의 공식으로 바꾸어 주면 다음과 같다.
근을 구하는 판별식
광선이 도형이 충돌했냐에 대한 판정은 근의 유무에 달렸다. 근이 존재한다면 해당 광선, 방정식은 원과 충돌한다는 의미가 되기 때문이다. 이를 판별하는 판별식은 다음과 같다.
근의 공식에서 근의 유무는 해당 판별식으로 판단한다.
광선을 쏘았을 때 이 값이 0보다 같거나 크다면 광선이 원과 충돌한 것이고 0보다 작을 경우 충돌하지 않았다고 판단할 수 있게 된다.


이를 코드로 옮기면 다음과 같다.
// hit_sphere.c
t_bool hit_sphere(t_sphere *sp, t_ray *ray)
{
t_vec3 oc; // 0에서부터 벡터로 나타낸 구의 중심.
//a, b, c는 각각 t에 관한 근의 공식 2차 방정식의 계수
double a;
double b;
double c;
double discriminant; //판별식
oc = vminus(ray->orig, sp->center);
a = vdot(ray->dir, ray->dir);
b = 2 * vdot(oc, ray->dir);
c = vdot(oc, oc) - sp->radius2;
discriminant = (b * b) - (4 * a * c);
printf ("a : %f, b: %f, c : %f, 판별식 : %f\n", a, b, c, discriminant);
// 판별식(내적의 값)이 0보다 크다면 광선이 구를 hit한 것!
// 내적이 양수 : cos 값이 양수, 예각
// 내적이 0 : cos 값이 0, 직각
// 내적이 음수 : cos 값이 음수, 둔각
return (discriminant > 0);
}레퍼런스
(6) Raytracing One Weekend 식 이해하기! 3
mini_raytracing_in_c/04.sphere.md at main · GaepoMorningEagles/mini_raytracing_in_c
