개요

백터의 내적을 구하는 공식은 다음과 같다.

그러나 MiniRT 관련 레퍼런스에서 벡터의 내적을 구하는 함수에서는 수식이 다르게 정의되어 있다.

double      vdot(t_vec3 vec, t_vec3 vec2)
{
    return (vec.x * vec2.x + vec.y * vec2.y + vec.z * vec2.z);
}

이는 벡터를 구하는 공식이 한 개가 아니기 때문이다.

벡터의 성분만 알고 각은 모를 때

기하학적인 의미를 보여주지는 않지만, 두 벡터 간의 내적이 벡터 크기 배율을 가진 벡터 간 각도의 코사인 임을 알 수 있다.

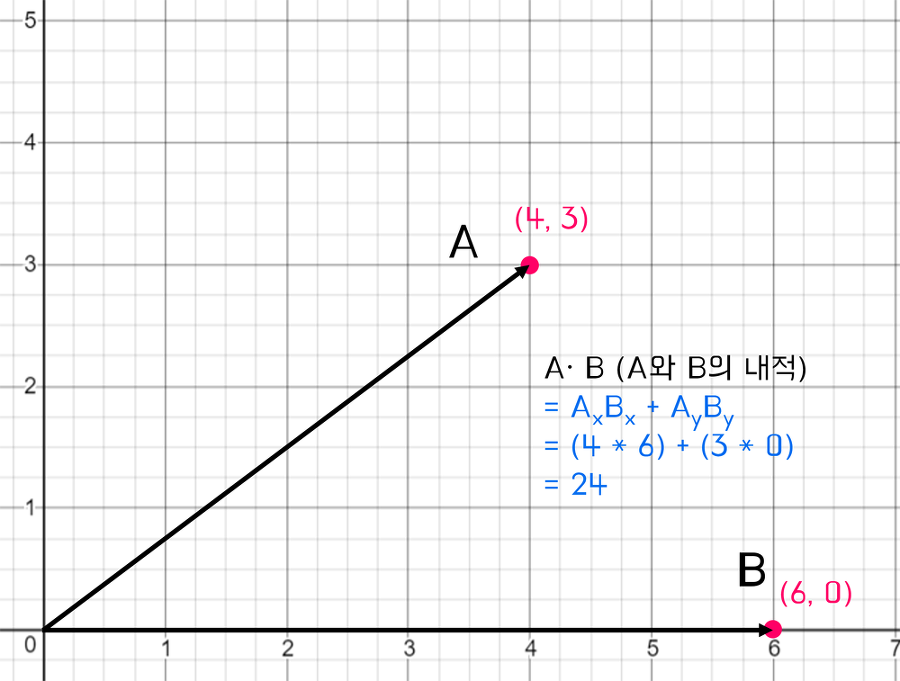
벡터의 성분과 각을 전부 알 때

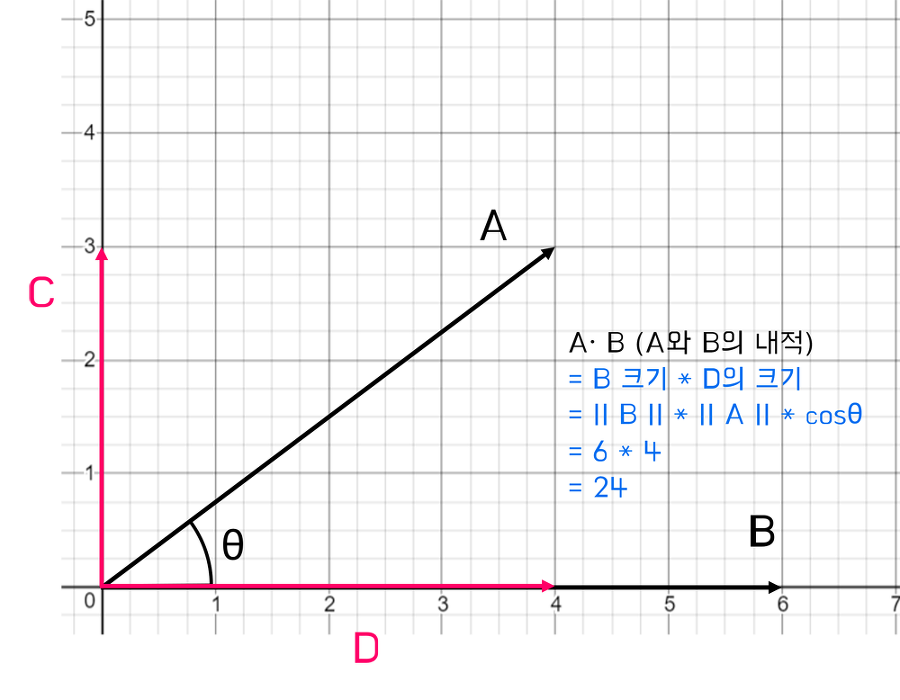
여기서 A의 크기가 아닌, A를 분해한 벡터 D의 크기를 곱해주는 이유는

B 벡터에 실제로 영향을 주는 벡터가 D이기 때문이다.

벡터 C는 벡터 B의 방향으로 어떤 영향도 주지 못하기 때문에, 내적 계산에서 무시한다.

백터의 내적의 특성

단위 백터끼리의 배적

단위 벡터끼리의 내적에서 u⋅v의 결과값은 두 벡터 간의 각도를 나타내게 된다.

단위 백터 구하기 - 벡터의 길이에 각 요소를 나누어주면 된다.

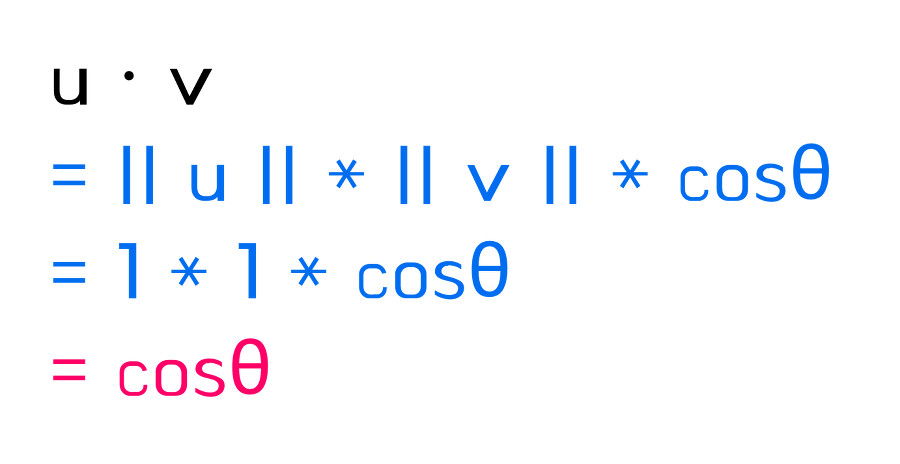
위와 같은 식이 성립할 수 있는 이유는 단위백터의 길이가 1이기 때문이다.

내적한 값은 코사인세타를 의미하는데, 이는 즉 두 벡터간의 각도를 가리키게 된다.

결과값이 0이라면, 두 벡터는 직각이다.

결과값이 0보다 크다면 두 벡터간 각도의 θ는 예각이다.

결과값이 0보다 작다면 두 벡터간 각도의 θ는 둔각이다.

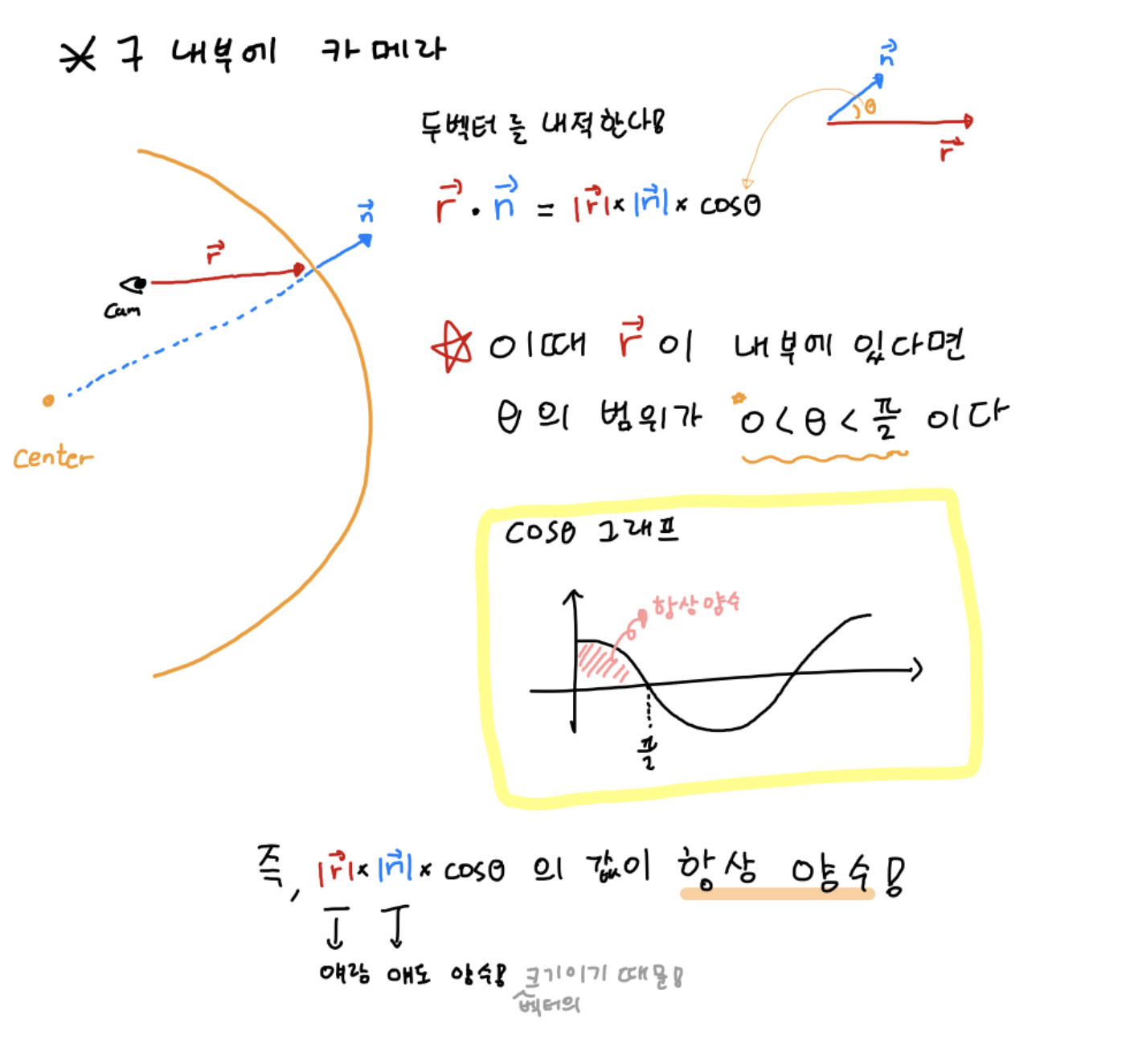
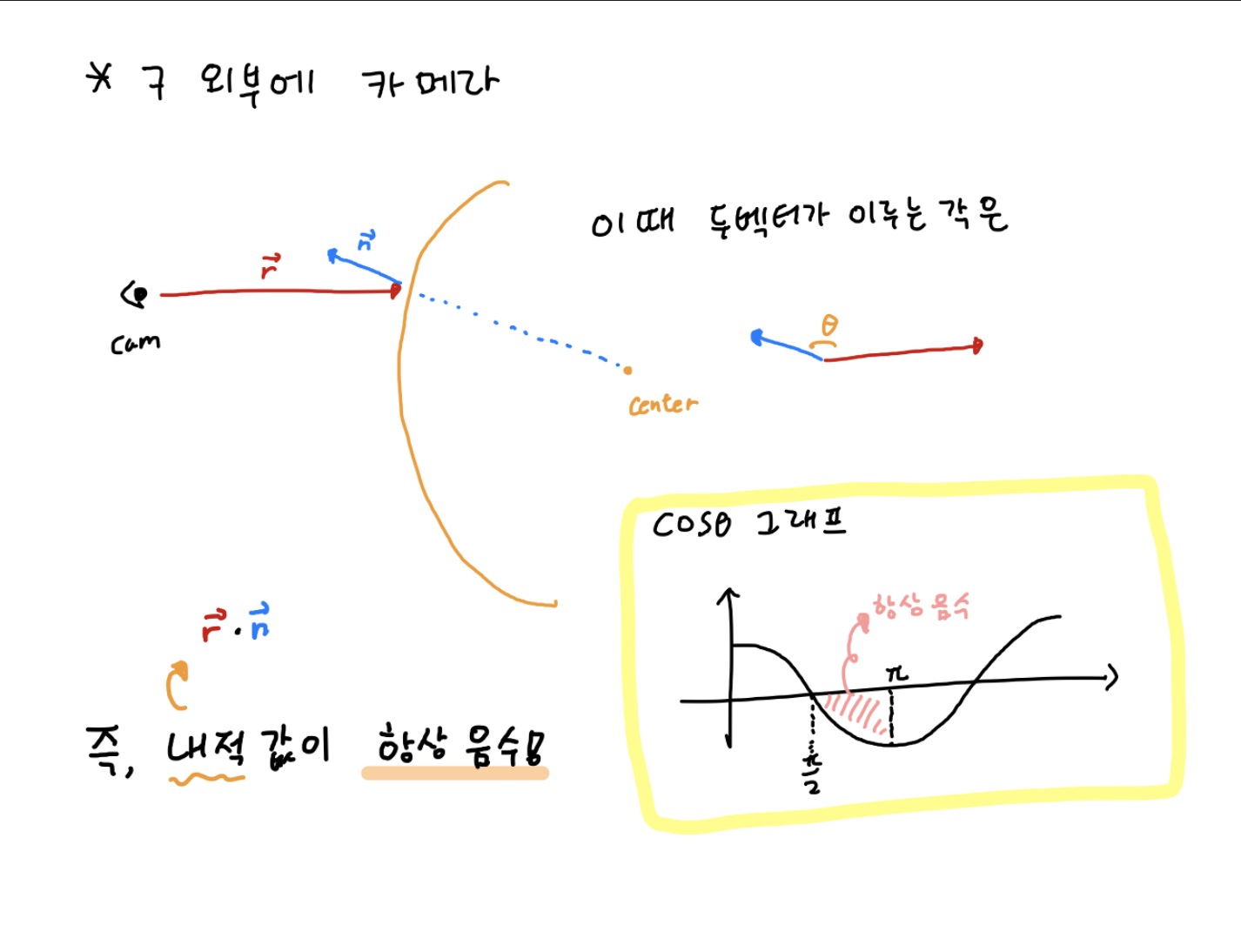
카메라가 구의 내부, 외부에 있냐에 따라 내적한 결과의 부호가 다르다는 것을 알 수 있고, 이를 토대로 광선이 안쪽에서 출발했는지 바깥에서 출발했는지를 구분할 수 있다.