두 포스팅에 걸쳐 Logistic 회귀에 대해 다루어보려고 합니다.
Logistic 회귀는 회귀를 이용하여 분류 문제를 해결하는 방법론인데요.
이를 이해하려면 먼저 Odds 에 대해 이해해야 합니다.
Odds?
Odds(오즈)는 확률에 관한 용어로, 어떤 사건이 일어날 확률을 라고 하면 이에 대한 Odds 는 다음과 같이 정의됩니다.
사건이 일어날 확률 를 사건이 일어나지 않을 확률 로 나누어주었죠.
즉, 사건이 일어나지 않을 확률에 대한 일어날 확률인 셈입니다.
그러나 이를 바탕으로 Odds 의 직관적 의미를 곰곰이 생각해보아도 명쾌한 해답을 얻기는 쉽지 않습니다.
직관적인걸로만 따지면
로 정의되는 확률을 따라가기가 쉽지 않죠.
그렇다면 식도 복잡하고 직관적이지도 않은 Odds 라는 개념을 왜 사용하는 걸까요?
[0, 1] [0, )
Odds 는 0 이상 1 이하의 값을 가질 수 있는 확률을 0 이상의 모든 실수에 일대일로 대응시킵니다.
특히 확률의 중심이라고 할 수 있는 을 곱하기의 중심이라고 할 수 있는 로 대응시키죠.
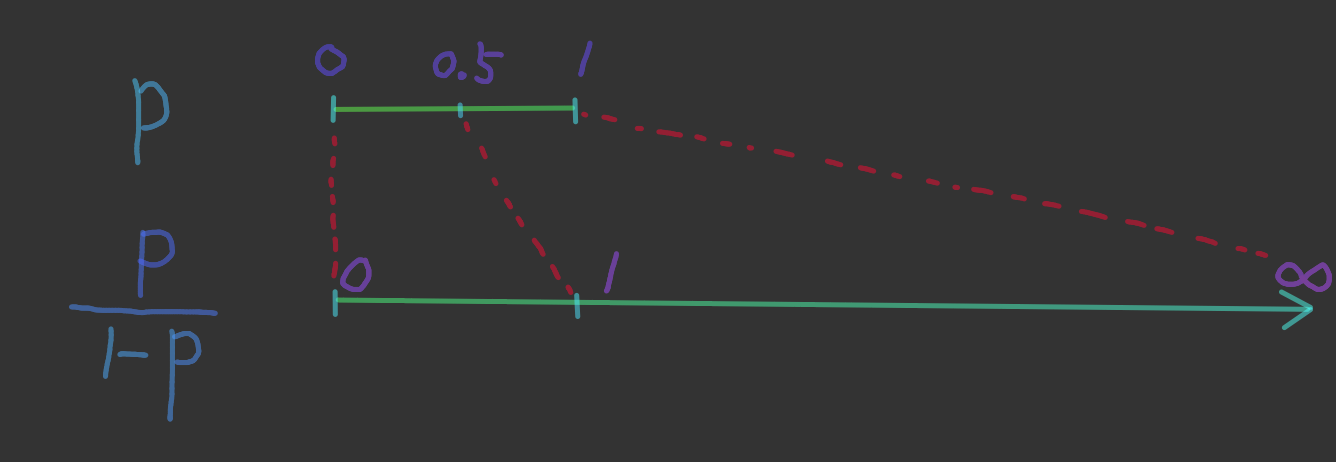
그런데 이렇게 대응시키고 보니 무언가 아쉬움이 남습니다.
원래 에서는 와 의 길이가 서로 같았는데 이 둘을 각각 대응시키고 보니
가 되어 둘의 길이가 서로 달라졌기 때문입니다.
log 를 씌워보자
비대칭 문제를 해결하기 위해 다음과 같이 생각해볼 수 있습니다.
과 를 서로 대칭이 되는 구간에 대응시키는 일대일 함수는 없을까?
만약 이런 함수가 있다면 Odds 를 이 함수에 넣으면 되기 때문이지요.
이때 머리를 스쳐가는 함수가 하나 있습니다.
바로 로그함수입니다.
로그함수는 을 으로, 를 로 대응시키죠. (여기서는 특별히 밑이 인 로그를 사용하였습니다)
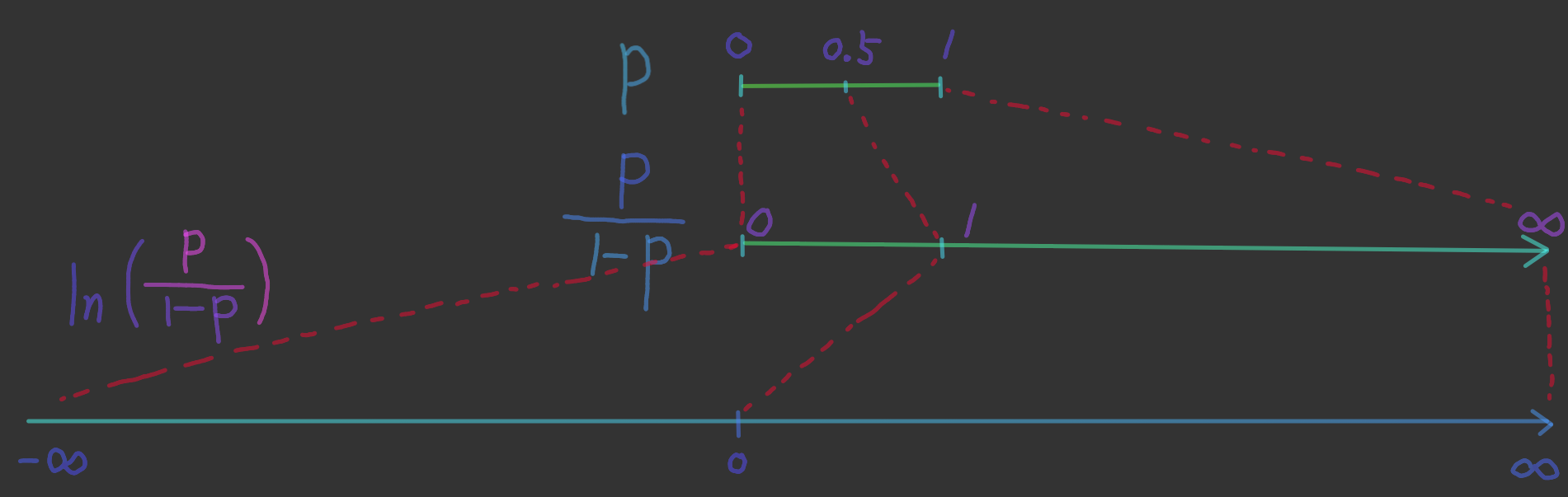
두 번의 대응을 마치고 나니 의 값을 가질 수 있는 확률이 로 고르게 대응되었습니다.
확률에서 가장 작은 값인 0은 로 대응되었고 확률에서 가장 큰 값인 1은 로 대응되었죠.
또한 확률에서 중앙에 해당하는 0.5는 덧셈의 중심에 해당하는 0으로 대응되었습니다.
이번 포스팅에서는 Odds 에 대해 알아보았습니다.
더불어 가 을 로 고르게 대응시킨다는 것을 살펴보았는데요.
다음 시간에는 오늘 다룬 내용을 바탕으로 Logistic 회귀에 대해 본격적으로 알아보겠습니다.
감사합니다.
다음 포스팅
https://velog.io/@shh0422/Logistic-%ED%9A%8C%EA%B7%80-Logistic-%ED%9A%8C%EA%B7%80
