CH4에서 모델의 일반화 성능을 판단(overfitting과 underfitting 판단)하기 위해 learning curve들을 그렸음. 이후 일반화 오차와 bias-variance trade-off에 대해 언급했는데 설명이 부족하다고 느껴 찾아봄
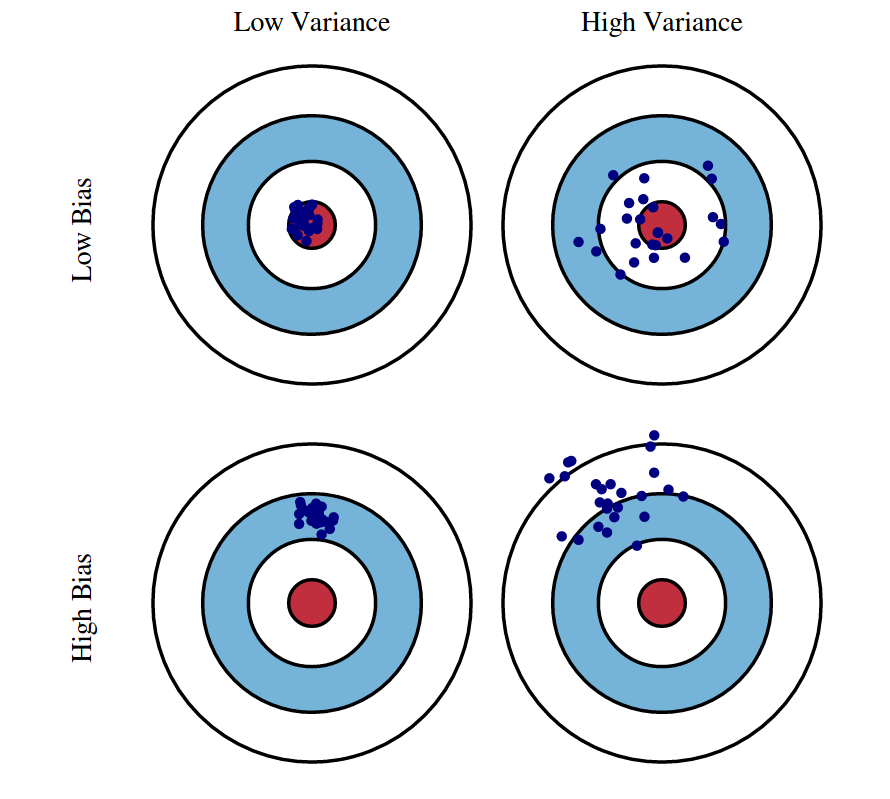
과녁판의 가운데는 정답값이 있는 곳이고, 과녁판에 찍힌 점들은 예측값들이다. Bias 오차가 높은 경우 예측값이 정답값에서 멀어져있고 Variance 오차가 높은 경우 예측값의 분포가 넓게 퍼져있다.
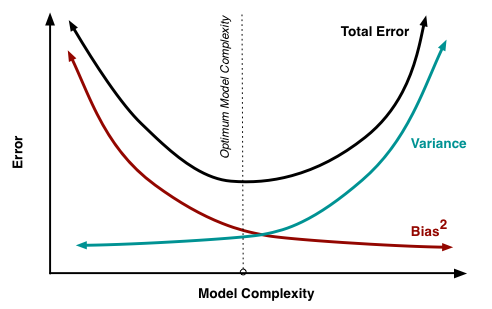
모델 복잡도에 대한 bias 오차와 variance 오차의 variation이다. bias 오차와 variance 오차가 하나가 증가하면 다른 하나는 감소하는 trade-off 관계임을 확인할 수 있다.
또한 모델의 복잡도가 클수록 variance 오차는 커지고, 복잡도가 작을수록 bias 오차가 커지는 것으로 보아 이는 모델의 overfitting과 underfitting과 관련되어 있음을 알 수 있다. 즉, variance 오차가 클수록 모델은 overfitting 하기 쉽고, bias 오차가 클수록 underfitting 하기 쉽다.
| 오차 | Model Complexity | 적합성 |
|---|---|---|
| Bias 오차가 낮음 & Variance 오차가 높음 | 복잡 | overfitting |
| Bias 오차가 높음 & Variance 오차가 낮음 | 단순 | underfitting |
이 관계는 slope으로도 표현할 수 있다.
우리는 모델의 overall 오차를 찾아야 하므로 이 두 오차의 "sweet spot"을 찾으면 되고, 이는 위 그래프에서 optimum이라고 나타낸 지점이다.
아래의 test error의 decomposition을 도출하기 위해 엄청난 수학적 풀이가 있었지만.. 건너뛰고 결론만 보면.. expected test error는 variance 오차, bias(정확히는 bias의 제곱이지만) 오차, 그리고 noise 오차로 구성됨을 수식으로 확인할 수 있다.
*noise는 irreducible error라고 하는데 이는 데이터 측정할 때부터 기계 결함 등으로 생겼기 때문
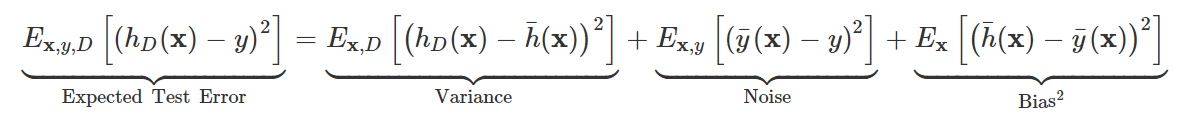
마지막으로, 우리는 저 optimum 지점을 어떻게 구할 수 있을까? 답은 훈련 세트 외에 일반화 성능을 테스트 할 수 있는 검증 세트를 만들어서 prediction error를 구한 후, 검증 세트의 오류가 증가하기 시작하기 전인 지점을 찾으면 된다.
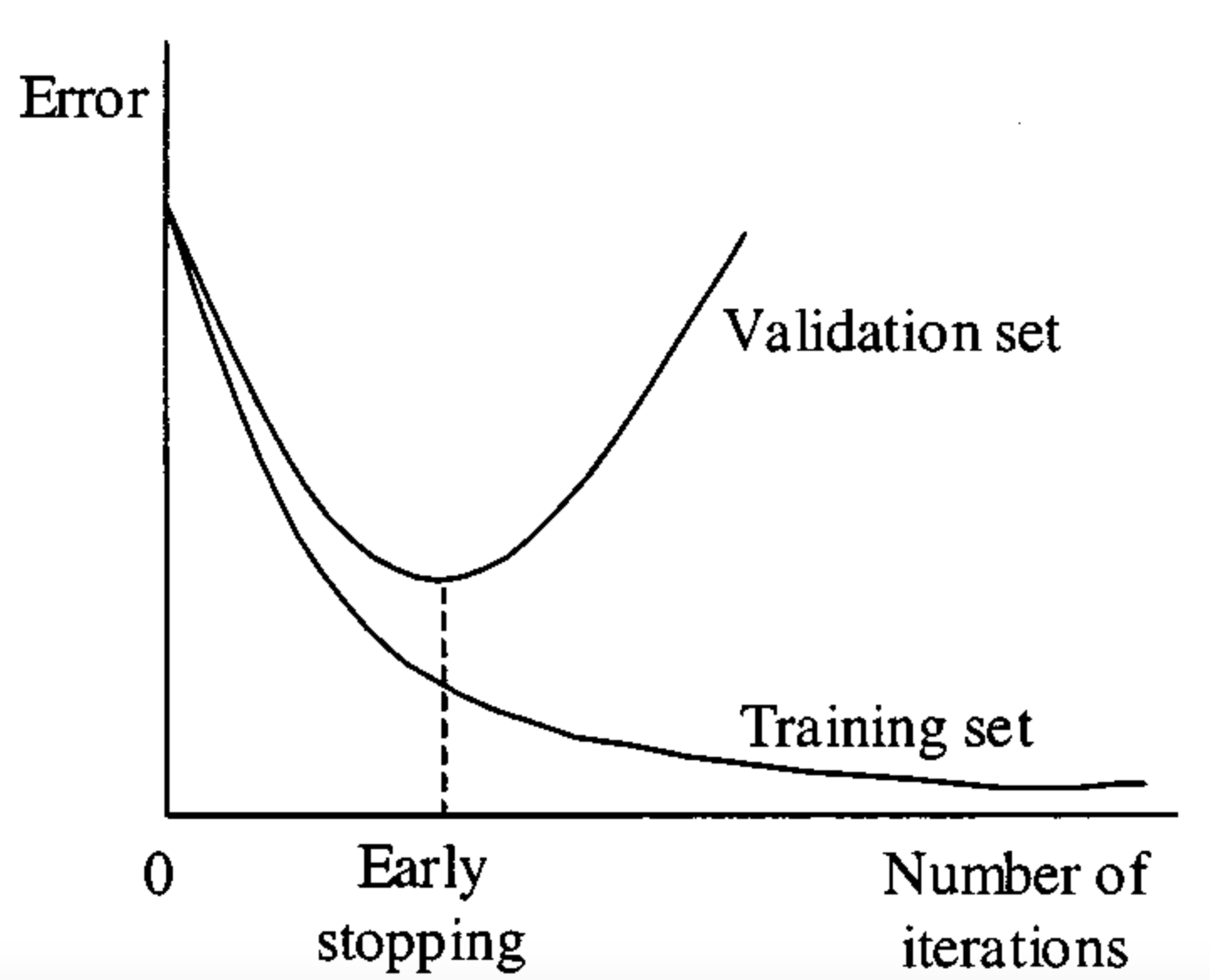
출처: https://paperswithcode.com/method/early-stopping
출처:
https://datacookbook.kr/48
https://scott.fortmann-roe.com/docs/BiasVariance.html