[ML] Regularization : 이것만 보면 됨

shihyunlim·2024년 9월 30일

Machine Learning

목록 보기

18/20

https://velog.io/@shihyunlim/ML-Regularization-no6or2cr
이전에 규제에 대해 공부한 적이 있어서 내용 수정 및 추가만 하려고 했는데 고칠 게 좀 많아 보여서 새로 정리하려고 함^-^

L2 norm과 L1 norm의 정의 참고
https://hwanii-with.tistory.com/58

1) Ridge Regression

릿지 회귀의 비용 함수

J(\theta)=\text{MSE}(\theta)+\frac{\alpha}{m}\sum_{i=1}^{n}\theta_i^2

릿지 회귀(또는 티호노프 규제)는 규제가 추가된 선형 회귀 버전임
규제항: $\frac{\alpha}{m}\sum_{i=1}^{n}\theta_i^2$
- 데이터에 맞추는 것뿐만 아니라 모델의 가중치가 가능한 작게 유지되도록 함
- 훈련 중에만 비용 함수에 추가됨. 훈련이 끝나면 규제가 없는 비용 함수로 평가함
- $\alpha$ 는 규제 정도를 조절. $\alpha$ 가 0에 가까울수록 규제 정도가 낮은 것, 값이 클수록 규제 정도가 커져서 선형 회귀의 경우 수평선에 가까워지며 다항 회귀의 경우 그래프가 단순해짐
편향 $\theta_0$ 는 규제되지 않음. summation은 $i=1$ 에서 시작함
$\mathbf{w}$ 를 특성의 가중치 벡터( $\theta_1$ 에서 $\theta_n$ )라고 정의하면 규제항은 $\alpha(\left\| \mathbf{w} \right\|_2)^2/m$ 와 같음
- $\left\| \cdot \right\|_2$ : 가중치 벡터의 L2 norm
- 배치 경사 하강법에 적용하려면 특성 가중치에 대한 MSE 그레이디언트 벡터에 $2\alpha\mathbf{w}/m$ 를 더하면 됨. 편향의 그레이디언트에는 어떤 것도 더하지 않음

릿지 회귀의 normal equation

\hat{\theta}=(\mathbf{X}^T\mathbf{X}+\alpha\mathbf{A})^{-1}\mathbf{X}^T\mathbf{y}

선형 회귀와 마찬가지로, 릿지 회귀를 계산하기 위해 정규 방정식과 경사 하강법 모두 사용 가능
- $\mathbf{A}$ 는 편향에 해당하는 맨 왼쪽 위의 원소( $\theta_0$ )가 0인(규제에 포함되지 않기 위함), (n+1)x(n+1)의 identitiy matrix(단위 행렬, 주대각선이 1이고 나머지가 모두 0인 square matrix)임
- Ridge의 solver 매개변수의 default는 auto지만, 희소 행렬이나 singular matrix(특이 행렬)이 아닐 경우 cholesky가 됨. Cholesky decomposition을 이용하여 정규 방정식을 더 간단하게 바꾸어 계산할 수 있음
- SGDRegressor에서는 penalty 매개변수를 l2로 지정하면 됨
RidgeCV 클래스: 릿지 회귀를 수행하지만 교차 검증을 사용하여 하이퍼파라미터를 자동으로 튜닝. GridSearchCV와 거의 비슷하지만 릿지 회귀에 최적화. LassoCV와 ElasticNetCV도 있음

2) Lasso Regression

라쏘 회귀의 비용 함수

J(\theta)=\text{MSE}(\theta)+2\alpha\sum_{i=1}^m\left\vert \theta_i \right\vert

선형 회귀의 또 다른 규제된 버전
- 비용 함수에 규제항으로 L1 norm을 더함
lasso(least absolute shrinkage and selection operator)
- 중요 특징! 덜 중요한 특성의 가중치를 제거하려고 함. 가중치가 0이 됨
- 즉, 자동으로 feature selection을 수행하여 sparse model(0이 아닌 특성의 가중치가 적음)을 만듦
lasso 비용 함수는 $\theta_i=0(i=1, 2, ..., n)$ 에서 미분 가능하지 않음. 하지만 subgradient vector $g$ 를 사용하면 경사 하강법을 적용하는 데 문제 없음
- 추가 설명! ridge는 L2 규제를 써서 항상 미분 가능하므로 최적점에 비교적 매끄럽게 도달하지만, lasso는 L1 규제를 써서 특정 회귀 계수가 0인 경우 미분 불가능하기 때문에 불연속 발생

라쏘 회귀의 subgradient vector

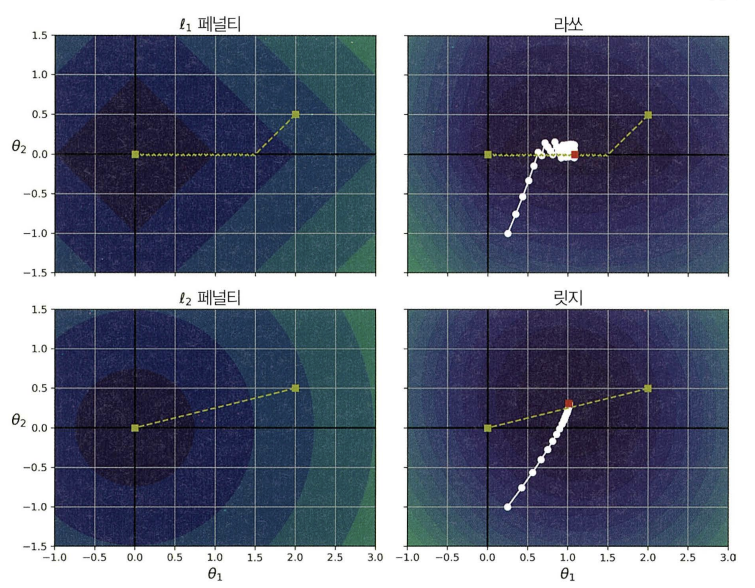
g(\mathbf{\theta}, J)=\nabla_\theta \text{MSE}(\mathbf{\theta})+\alpha\begin{pmatrix} \text{sign}(\theta_1) \\ \text{sign}(\theta_2) \\ \vdots \\ \text{sign}(\theta_n) \end{pmatrix}, \quad \text{sign}(\theta_i)=\begin{cases} -1 \quad \text{when} \space \theta_i<0 \\ 0 \quad \text{when} \space \theta_i=0 \\ +1 \quad \text{when} \space \theta_i>0 \end{cases}

사진 출처: 핸즈온 머신러닝 3판

이 그래프 해석이 그렇게 어려웠는데 이제는 쉽게? 할 수 있다!
모델은 회귀 계수로 $\theta_1$ 과 $\theta_2$ 를 갖는다. 맨 왼쪽 위는 L2 패널티를 적용한 건데, $\theta_1=2.0$ , $\theta_2=0.5$ 에서 출발하며 덜 중요한 가중치인 $\theta_2$ 가 0이 되는 방향으로 가다가 0에 도달하면 길을 따라서 $\theta_1$ 가 0이 되는 방향으로 이동한다. 오른쪽 위의 Lasso 회귀는 이런 L1 norm을 적용한 것으로 $\theta_1=0.25$ , $\theta_2=-1.0$ 에서 출발하여 마찬가지로 더 작은 값인 $\theta_2$ 가 0이 되는 방향으로 이동한 후 0에 도달하면 L1의 특성으로 인해 진동을 하기는 하지만 비로소 global minima에 도달한다.
다음은 왼쪽 아래를 보자. L2 손실은 원점에 가까울수록 줄어든다. 따라서 경사 하강법은 원점까지 직선 경로를 따라간다. 오른쪽 아래를 보면 global minima에 가까워질수록 그레이디언트가 작아진다.

진동하는 것을 제한하여 라쏘 회귀보다 빠르게 수렴 가능
$\alpha$ 를 증가시킬수록 최적의 파라미터가 원점에 가까워지지만 완전히 0이 되지는 않는다!

3) Elastic Net

릿지 회귀와 라쏘 회귀를 절충한 모델
- 규제항은 릿지 회귀와 라쏘 회귀의 규제항을 더한 것
- 혼합 비율 r로 혼합 정도를 조정. r=0이면 릿지 회귀와 같아지고, r=1이면 라쏘 회귀와 같아짐
- ElasticNet 클래스에서는 l1_ratio가 r과 동일

엘라스틱넷 비용 함수

J(\theta)=\text{MSE}(\theta)+r(2\alpha\sum_{i=1}^m\left\vert \theta_i \right\vert)+(1-r)(\frac{\alpha}{m}\sum_{i=1}^{n}\theta_i^2)

When to use? 규제가 약간 있는 것이 좋으므로 일반적인 선형 회귀는 피해야 함. 릿지가 기본이 되지만 몇 가지 주요한 특성만 뽑고자 한다면 라쏘나 엘라스틱넷이 나음. 그러나 특성 수가 훈련 샘플 수보다 많거나 특성 몇 개가 강하게 연관된 경우(multi collinearity?) 보통 라쏘가 문제를 일으키므로 엘라스틱넷이 좋음!

4) Early Stopping

경사 하강법과 같은 iterative learning algorithm에서 사용
검증 오차가 최솟값에 도달했을 때 훈련 중지시킴
- 학습 오차는 계속해서 줄어들고, 검증 오차는 감소하다가 커지는 지점이 있는데 이는 훈련 데이터에 overfitting 하다는 것. 그러므로 검증 오차가 최소에 도달했을 때 모델을 조기 종료해야 함
- GD 글에서 SGDRegressor의 파라미터로 설정할 수 있었음. (SGDClassifier도 됨)

출처: 핸즈온 머신러닝 3판

shihyunlim

이전 포스트

[ML] Bias-Variance Trade-off

다음 포스트