모델이 학습데이터에 너무 잘 맞으면 overfitting이 일어난다. overfitting은 모델의 일반화 성능을 낮추기 때문에 규제를 통해 줄여야 한다.
regularization의 방법은 다양하다. 그 중 이번에 다룰 방법은 linear model에 적용할 수 있는, 모델의 weight에 제한을 거는 방법인, Ridge Regression, Lasso Regression, 그리고 Elastic Net에 대해 다뤄볼 것이다.
추가로 마지막에는 GD와 같은 iterative learning algorithm에 적용할 수 있는 Early Stopping과 같은 규제도 다루려고 한다.
1) Ridge Regression
Ridge Regression은 multicollinearity 문제로부터 나왔다.
linear regression model은 형식을 가진다. 여기서 Y는 predicted value(dependent variable), X는 predictor(independent variable), B는 X에 곱해진 regression coefficient, 는 X가 모두 0인 경우 dependent variable의 값이다(y-intercept).
multicollinearity란 이런 independent variable간에 상관관계가 있을 때 일어난다. 예를 들어, 택배가 거리가 가까울수록 적은 수의 물건이 배달되고, 멀수록 물건이 많이 배달된다고 하자. 여기서 거리와 배달되는 물건의 수는 상관관계를 가지며, 이 두 피처가 모델의 independent variable일 경우 multicollinearity가 발생한다.
이 문제를 해결하는 방법으로는 diversified data를 더 모으는 것, sample size를 키우는 것, independent variable의 수를 줄이는 것, 다른 모델을 적용하는 것 등이 있지만 multicollinearity를 항상 해결하지는 못한다고 한다. 그래서 등장한 방법이 ridge regression이다.
예측 모델을 만들 때 coefficient는 아래와 같은 normal equation으로 구할 수 있으며, 최선의 coefficient는 residual sum of squares(RSS)가 최소화되는 경우에 구할 수 있다. 이 방법을 Ordinary Least Squares(OLS)라고 한다.
그런데 만약 둘 이상의 variable들이 상관관계를 가진다면 OLS는 high-value coefficient()를 반환하게 될 것이다. 모델이 큰 coefficient를 가지게 된다면 모델은 input의 작은 변화에도 잘 바뀌게 될 것이다. 즉, 모델이 overfitting 하게 될 것이다.
이런 문제를 해결하기 위해 Ridge regression은 잠재적으로 상관된 predictor들을 고려하여 OLS의 계수 계산 방식을 수정한다. 구체적으로, RSS 함수에 regularization term(or a penalty term)을 덧붙여 높은 값의 계수를 조정한다. 이 penalty term은 모델의 coefficient의 제곱을 모두 더한 값이며, penalty term의 정도는 하이퍼파리미터 로 통제할 수 있다.
L2 penalty term은 coefficient들의 값을 줄이는데, 원래 값의 비율에 따라 더 큰 값들을 더 많이 줄이게 된다. 더불어 가 커지면 high-value coefficient들은 더더 작아진다. 결과적으로 ridge estimator는 overfitting을 줄인 값을 반환하게 된다.
여기부터는 교재에 나온 내용 중 추가할 것만
- 위 글에서는 RSS(잔차제곱합)에 규제를 더했지만, 책에서는 MSE(평균제곱오차)에 규제를 더함! 차이 있음!
- 교제에서는 coefficient를 B 대신 theta를 사용
- RSS_L2 함수는 penalty term이 더해진 오차 함수
- 책에서 RSS_L2의 penalty term 앞에 1/2가 곱해져 있는데, 지피티 말로는 수학적 계산의 용이성을 위해 있는 거라 안 써도 된다고 함
- 대부분의 regularized model은 input feature들의 크기에 민감하기 때문에 ridge regression을 하기 전에 StandardScaler 등으로 scaling 해줘야 함
- Ridge Regression closed-form solution :
- closed-form solution(a variant of normal equation using a matrix factorization technique by Andre-Louis Cholesky)을 사용

- SGD에도 적용할 수 있음. 오차 함수에 l2 penalty term을 추가한 것

2) Lasso Regression
내용 출처: https://www.ibm.com/topics/ridge-regression
https://www.ibm.com/topics/lasso-regression
Ridge Regression은 coefficient를 0에 가까이 줄이지만 0으로 만들지는 않는다. coefficient를 0으로 만드는 건 "paired" predictor를 효과적으로 없애는 방법이며, 이 작업을 feature selection이라고 한다. (얘도 multicollinearity를 고치는 것!!) 그 말은 Ridge Regression이 feature selection을 하지 않는다는 것이며 ridge 회귀의 disadvantage라고도 한다.
Lasso는 Least Absolute Shrinkage and Selection Operator를 의미한다. 이는 머신러닝에서 automatic feature selection을 용이하게 하기 때문에 고차원 데이터를 다루는 데 쓰인다.
Lasso에서는 RSS에 회귀 coefficient들의 절대값을 모두 합한 L1 penalty term을 추가한 오차함수를 사용한다. 를 통해 규제 정도를 조정하는 점은 Ridge와 동일하다. L1 penalty는 계수를 0으로 줄여 independent variable을 효과적으로 제거할 수 있다는 점과 모델의 sparsity를 촉진한다는 점을 특징으로 가진다.
Limitations of lasso regression
Lasso regression can handle some multicollinearity without negatively impacting interpretability of the model, but it cannot overcome severe multicollinearity4. If covariates are highly correlated, lasso regression will arbitrarily drop one of the features from the model. Elastic net regularization is a good alternative in this situation.
-> 이 글에서 알 수 있듯 Lasso 회귀는 어느 정도의 multicollinearity를 처리할 수 있으며, 모델의 해석 가능성에 부정적인 영향을 주지 않지만, severe multicollinearity를 극복할 수는 없다. 만약 variable들이 높은 상관관계를 가진다면, Lasso 회귀는 모델에서 임의로 하나의 feature를 제거할 것이다.(중요한 피처를 없앨 수도, 덜 중요한 피처를 남길 수도 있음) 글의 마지막 부분에서는 Elastic Net 규제가 좋은 대안이 될 수 있음을 암시한다.
- 책에 나온 코드

의문점
ridge 회귀는 coefficient가 0에 가까울 정도로 작아지고, lasso 회귀는 작아지다가 0이 되기도 한다고 했는데, 이게 오차함수에 각각의 penalty term(L2, L1)을 추가한 식과 어떤 관련이 있을까?
지피티가 뭐라뭐라 알려주긴 했는데 설명 중에 "미분의 연속성"이라는 말이 포함돼서 미분이 연속적인 게 여기서 무슨 상관이냐고 물어봤다.
1. Ridge 회귀와 미분의 연속성
Ridge 회귀의 손실함수는 L2 규제항 을 포함한다. 이 식을 미분하면 다음과 같다. (위에서는 B라고 표기했지만 여기서는 로 쓰겠음)
여기서 중요한 점은 에 대한 미분 값이 선형적이며, 에 대해 연속적이라는 것이다. 즉, Ridge 회귀의 손실함수는 가 0에 가까워질수록 점진적으로 감소하지만, 절대적으로 0이 되도록 하는 힘이 없다. 대신 가 충분히 작은 값으로 유지되도록 한다. 이는 미분이 연속적이어서 어떤 도 정확히 0이 되도록 강제할 요소가 없다는 의미다.
2. Lasso 회귀와 미분의 불연속성
반면 Lasso 회귀의 손실함수는 L1 규제항 을 포함한다. 이 식을 미분하면 다음과 같다.
여기서 는 의 부호를 나타내며, 다음과 같이 정의된다.
이 규제항이 중요한 이유는 절대값 함수가 미분할 때 불연속점을 가진다는 점이다. 절대값 함수의 그래프를 그려보면, 0을 중심으로 V자 모양을 한다. 이는 0 근처에서 함수가 급격하게 변한다는 것을 의미한다. 가 0보다 클 때, 의 미분값은 +1, 가 0보다 작을 때, 의 미분값은 -1이다. 하지만 가 정확히 0일 때는 미분이 정의되지 않으며, 이 점에서 함수의 변화가 불연속적이다.
왜 가 0이 되는거지? Lasso 회귀는 이 불연속점을 이용한다. 모델이 학습되는 과정에서 가 작아지다가 0에 가까워지면, 이때 L1 규제가 를 더 작게 만들기 위해 추가적으로 압력을 가하여 0이 되어버린다.
아까부터 "힘", "강제", "압력"이라는 말을 사용하는데, 도대체 압력이 어떻게 가해진다는 거지? L1 규제는 절대값을 사용하기 때문에 회귀 계수 가 0에 가까워질수록 그 값을 더 낮추는 방향으로 "압력"이 가해진다. 양수 영역: 만약 이면, L1 규제는 의 추가적인 페널티를 부과하여 그 값을 더 낮추려는 압력을 가한다. 음수 영역: 이면, L1 규제는 의 페널티를 부과하여 를 증가시키려는 압력을 가한다. 0 근처: 가 0에 매우 가까워지면, 가 0이 되는 것이 손실함수의 값을 최소화하는 가장 좋은 방법이 된다. 이는 회귀 계수가 더 이상 줄어들지 않고 0으로 설정되는 것을 의미한다. 결국 "압력"이란 손실 함수 최적화 과정에서 L1 페널티가 작동하는 방식이다.
3) Elastic Net
Elastic Net은 Lasso의 feature selection 기능을 유지하면서도 Ridge 회귀를 결합하여 높은 상관관계의 변수들을 균형있게 처리할 수 있다. 규제항은 ridge와 lasso의 규제항의 mix이고, mix ratio 을 통해 조절할 수 있다. 이면 elastic net은 ridge 회귀와 동일하고, 이면 lasso 회귀와 동일하다. 아 그래서 elastic하다는 거구나
(위 내용을 읽었다면 MSE, theta를 사용해도 이해상 큰 어려움은 없을 것이라고 생각)
- 책에 나온 코드

When to use?
plain linear regression, ridge, lasso, or elastic net 중에 언제 어떤 걸 사용해야할까? 일반적으로 규제가 어느정도 있는 것이 좋으므로 plain은 피하고, ridge는 default로 좋다. 만약 일부 피처만 유용하다면 lasso나 elastic net을 사용하는 것이 좋다. 그런데 elastic net은 피처의 수가 instance의 수보다 큰 경우와 일부 피처들 사이에 상관관계가 severe할 때 더 효과적으로 작동하므로, 일반적으로 lasso보다 더 선호된다.
어라? 공부할 게 더 있었네..?

더 깊게 안들어가고 싶은데.. 이미 본 이상 어쩔 수 없다.. 잠시 보류..
[인사이드 머신러닝] 대표적인 규제(Regularization)기법들 (Ridge, Lasso, Elastic-Net)
by.cleansky
4) Early Stopping
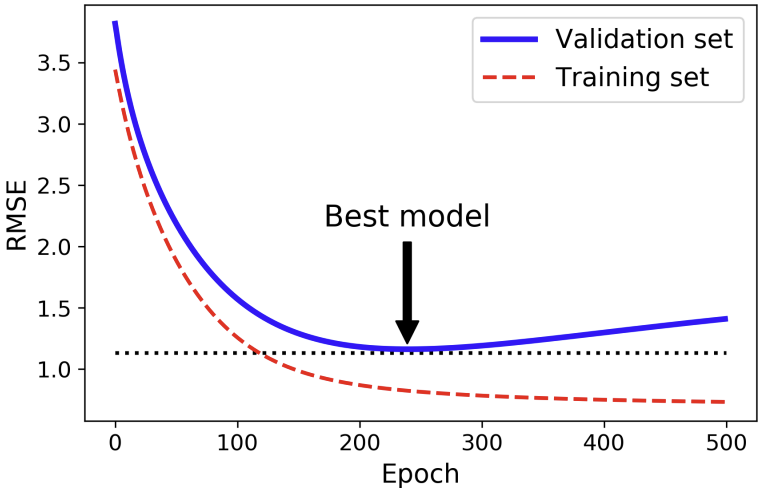
이 방법은 Gradient Descent와 같이 iterative learning algorithm에서 validation error가 minimum에 이르렀을 때 멈추는 것이다. 이후 모델은 training set에 과적합되기 때문에 training error는 계속해서 감소하고, validation error는 증가하게 된다.
- 코드
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)), # nonlinear data를 학습할 때에도 linear model을 사용 가능, 데이터 feature들의 거듭제곱 항들을 추가
("std_scaler", StandardScaler()),
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter=1, warm_start=True, penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
sgd_reg.fit(X_train_poly_scaled, y_train)
y_train_predict = sgd_reg.predict(X_train_poly_scaled)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
train_errors.append(mean_squared_error(y_train, y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])- 결과
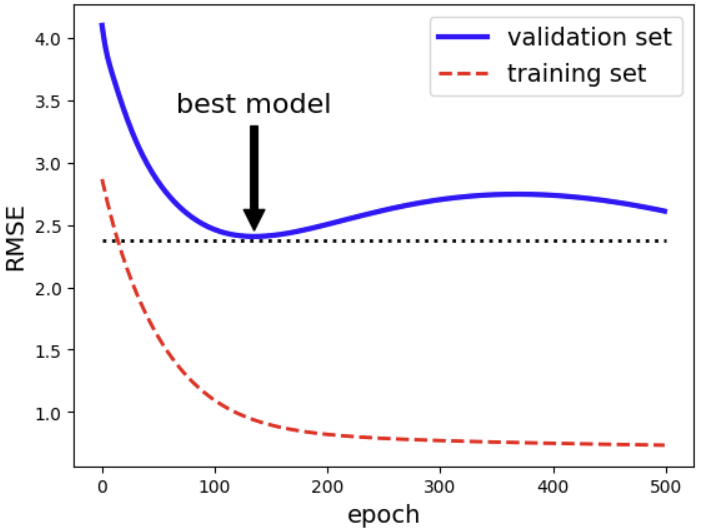
출처: Hands-On Machine Learning by Aurelien Geron