여태까지 SVM은 분류에만 사용되는줄 알았는데, 책 첫문단 읽고 나서 SVM이 linear or nonlinear classification, regression, outlier detection에 모두 사용된다는 걸 알고 조금 충격받았다,,
1) Linear SVM Classification
그림으로 알아보자. 왼쪽 그림부터 보면, 세 구분선 중 점선은 두 피처를 분류하는데 최악인 것을 볼 수 있다. 나머지 두 선들은 두 피처를 분류하기는 하지만, 점들과의 거리가 매우 가깝기 때문에 새로운 데이터가 들어왔을 때 맞지 않을 수 있어서 overfitting의 우려가 있다. 반면 오른쪽 그림의 직선은 두 피처를 잘 분류할 뿐만 아니라 가장 가까운 학습셋들과의 거리가 가장 멀리 떨어져 있는 것을 볼 수 있고, 이 직선이 바로 SVM Classifier의 decision boundary가 된다. 두 점선 사이를 "street"이라고 하면, 결정선의 street이 가장 wide한 경우라고 볼 수 있으며, 이는 large margin classification이라고 불린다.

그럼 support vector란 뭘까? "off the street"에 새로운 데이터가 들어온다한들 결정선은 아무런 영향을 받지 않을 것이다. 그 이유는 street의 가장자리에 있는 instance들에 의해 완전히 구분되고(="supported") 있기 때문이다. 결정선에 중요한 이 instance들이 바로 support vector들이다.
오해하면 안되는 건 support vector가 반드시 가장 끝에 있는 데이터포인트들이 아니라는 것
-> A support vector is a data point or node lying closest to the decision boundary or hyperplane. These points play a vital role in defining the decision boundary and the margin of separation.
1-1) feature scales
의 간격은 20이고, 의 간격은 1로 둘의 scale 차이가 매우 큼을 알 수 있다. SVM Classifier는 instance 간의 거리를 체크하므로 거리를 정확하게 측정하는 것이 중요하다. 그러므로 피처의 크기가 다를 경우, scaling을 진행하여 거리를 정확하게 측정하고, 결정선을 찾는 과정이 필요하다.
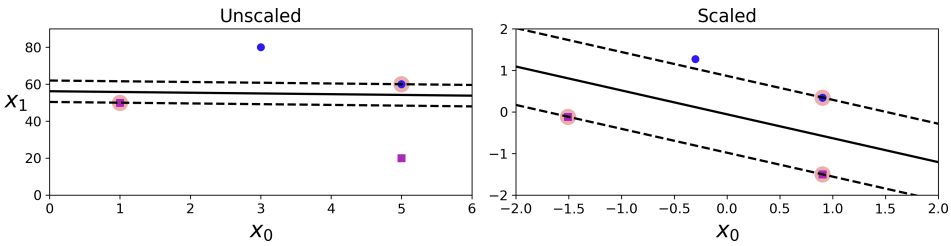
의문점: feature scaling의 방법으로 normalization과 standardization이 있다는 건 알겠는데, 왜 책이나 인터넷에서 standardization을 하는 StandardScaler를 더 많이 이용하는지 모르겠음
-> 간단하게 정리해보았음! Feature Scaling 오개념?을 짧게 말하자면 feature scaling을 할 때 normalization을 하는 거고, 그 종류들로 standardization(z-score normalization), min-max scaling가 있는 것임.
-> 그리고 결론으로 standarization을 사용하는 까닭은 아무래도 스케일링뿐 아니라 데이터를 평균=0로 centering도 하고 range 제한없이 표준편차만 1로 하기 때문이 아닐까 싶다!
1-2) Soft Margin Classification
모든 instance들이 off the street에 있어야 하고, 옳은 쪽에 있어야 한다고 하면 이는 hard margin classification라고 불린다. 이 경우는 데이터가 linearly seperable한 경우만 제대로 분류할 수 있으며, outlier에 매우 민감하다는 단점이 있다. 왼쪽 그림처럼 이상치가 존재하는 경우에는 분류가 불가능하며, 오른쪽처럼 존재하는 경우 support vector들과 결정선 사이가 매우 좁기 때문에 일반화가 힘들 것이다.
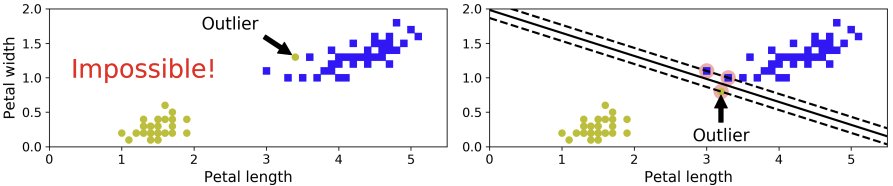
이런 문제를 피하려면 좀 더 유연한 모델을 만들어야 한다. 이 모델의 목적은 street을 최대한 크게 만드는 것과 margin violation을 제한하는 것의 균형을 이루는 것이 될 것이다. 다시 말해서 결정 경계선에 영향을 미치는 support vector들 간의 거리가 최대가 되는 것과 street 안으로 데이터 포인트들이 침해하는 것 사이에 균형을 이루어야 한다는 것이다.
사이킷런에서는 하이퍼파라미터 C를 이용해서 이 균형을 조절할 수 있다. 왼쪽 그림과 같이 C가 작으면 street은 커지지만, 이 안을 침해하는 데이터 포인트들이 많아진다(=margin violation이 커진다). 반면 C가 커지면 margin violation은 줄어들지만, street이 작아진다.
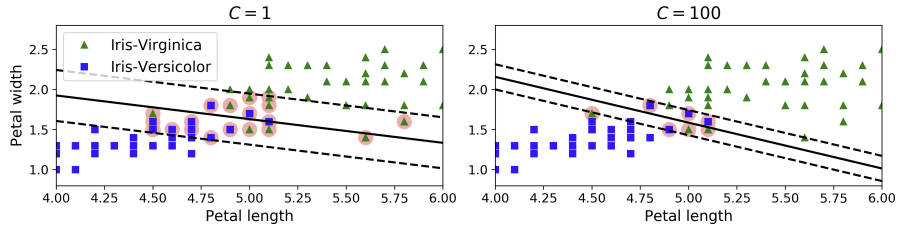
그런데 굳이 고르자면 둘 중에 어떤 C가 더 적합할까? 답은 왼쪽이다. 비록 margin violation이 크다고 하더라도 결정 경계선으로 분류가 제대로 이루어진 데이터 포인트들이 더 많기 때문이다.
추가로, 모델이 과적합한 경우 C를 낮춤으로써 규제를 가할 수 있다.
코드
- LinearSVC 클래스 ->
LinearSVC(C=1, loss="hinge") - SVC 클래스 ->
SVC(kernel="linear", C=1)- LinearSVC보다 느림
- SGDClassifier 클래스 ->
SGDClassifier(loss="hinge", alpha=1/(m*C))- 큰 데이터셋에 더 적합함, 수렴 속도는 느릴 수 있음
from skelarn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
svm_clf = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge")),
])추가 정보
- Logistic Regression Classifiers과 달리, SVM Classifiers는 각 클래스에 대한 확률을 반환하지 않음
- 책 p.158에서 "The LinearSVC class regularizes the bias term, so you should center the training set first by subtracting the mean."라고 언급되어 있는데, 도대체 why is centering related to regularizing the bias term in svm? 이 궁금한데 구글에 검색해도 안 나오길래 일단 stackoverflow에 물어본 상태,,
-> - 더 나은 성능을 위해 dual 파라미터는 False로 해야함
2) Nonlinear SVM Classification
2-1) Polynomial Features
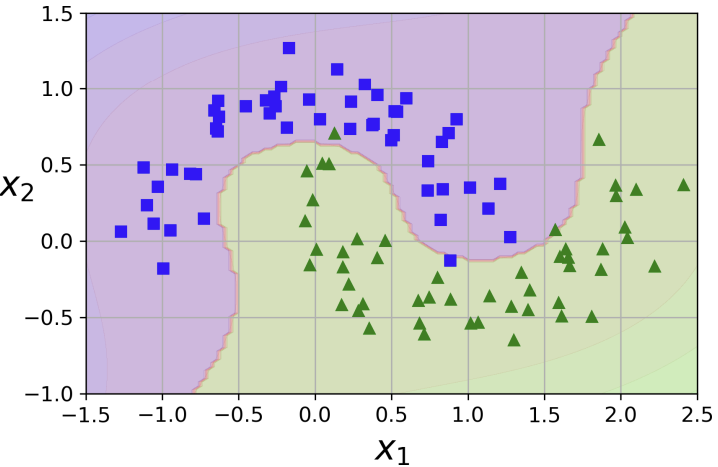
모든 데이터셋이 linearly seperable하지는 않다. 이런 nonlinear dataset의 경우에는 이전의 "polynomial regression"에서 봤듯 polynomial feature들을 추가해줄 수 있다. 왼쪽 그림에서 하나의 피처 은 선형적으로 나뉘지 않는다. 이때 새로운 피처 를 추가하면 오른쪽과 같이 선형적으로 나뉘는 것을 볼 수 있다.
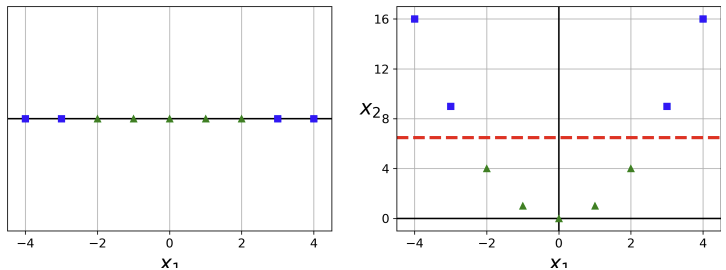
코드
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import Polynomialfeatures # 다항회귀에서 사용했던 것
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge")),
])
2-2) Polynomial Kernel
일반적으로 polynomial feature들은 쉽고 모델의 성능이 좋아지기 때문에 머신러닝 알고리즘에서 사용된다. 하지만 degree가 너무 낮은 경우에는 복잡한 데이터셋을 다루지 못하고, 너무 높은 경우에는 피처의 수를 엄청나게 증가시키고 모델을 느리게 한다.
SVM에서는 kernel trick이라고, polynomial feature들을 추가한 것과 같은 효과를 내지만 실제로 모델에 추가하지는 않는 방법이 있다. 그렇기 때문에 피처의 수가 폭발적으로 증가하는 것에 대한 걱정을 하지 않아도 된다. 이는 SVC 클래스를 통해 수행할 수 있다.
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])degree를 각각 3과 10으로 설정한 결과:
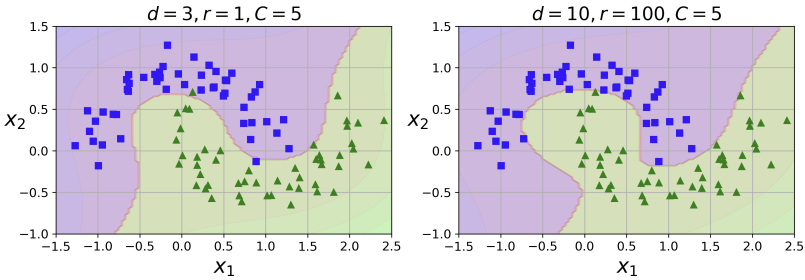
의문점
coef0의 역할이 "controls how much the model is influenced by high-degree polynomial versus low-degree polynomials"라고 했는데 원리 이해가 잘 안돼서 찾아봤다.
SVC 클래스에서 kernel은 linear, poly, rbf, sigmoid, precomputed인 경우에 사용되며 참고, coef0 매개변수는 polynomial과 sigmoid의 경우에만 사용된다. 참고
https://stackoverflow.com/questions/21390570/scikit-learn-svc-coef0-parameter-range
위 질문의 두 번째 답변을 기반으로 설명해보면, polynomial의 kernel function은 로 나타낼 수 있는데, 이때 p(=polynomial degree)가 무한대로 증가할수록 내적값이 1보다 작은 데이터 포인트쌍은 더 작아지게 되고 큰 데이터 포인트쌍은 더 커지게 되어 두 포인트 사이의 차이가 극대화되어 데이터가 과도하게 분리될 수 있다. 그렇기 때문에 coef0은 스케일링을 통해 데이터가 너무 많이 분리되지 않도록 한다.
추가로, grid search를 이용하면 적절한 하이퍼파라미터를 찾을 수 있다. 처음 범위는 거칠게(?) 잡고 여기서 괜찮은 값이 나오면, 이 값을 기준으로 세밀하게 찾으면 하이퍼파라미터를 효과적으로 찾을 수 있다고 한다!
2-3) Similarity Features
nonlinear 문제를 다루는 또 다른 방법은, 각 instance가 특정 landmark를 얼마나 닮았는지 측정하는 similarity function이다.
의 두 점 -2와 1을 landmark로 지정하자. 그 다음 를 갖는 Gaussian Radial Basis Function (RBF)을 유사도 함수로 지정하자.
참고
-> 이 책에서는 를 로 대신해서 나타냈지만, 실제 gaussian kernel function은 분포를 나타내는 sigma가 분모에 있는 가우시안 함수 형식을 가진다. 그리고 4)의 강의 필기에서 작성한 두 번째 커널식과 달리 위 함수는 이차식으로 이루어졌는데, 내 생각으로는 이것 또한 derivatives가 있으면 mathematically convenient하기 때문에 이차로 쓰지 않았나 싶다.
이 함수는 종 모양 함수로, landmark에서 가장 먼 지점인 0(similarity=1.00)에서 landmark에서 가장 가까운 지점인 1(similarity=0.00)까지 달라진다.
이제 새로운 feature들을 구해보자. 을 예로 들면, -1은 첫 번째 landmark()와 1 만큼, 두 번째 landmark()와 2만큼 떨어져 있다. 그러므로 새로운 feature들은 와 이 되며, 왼쪽 그래프에서도 확인할 수 있다.
오른쪽 그래프는 방금 한 작업을 의 instance들에 적용한 것으로, 기존의 피처들은 버려진 새로운 피처들로만 구성된 것이다. 이는 linearly seperable 하다는 것을 알 수 있다.
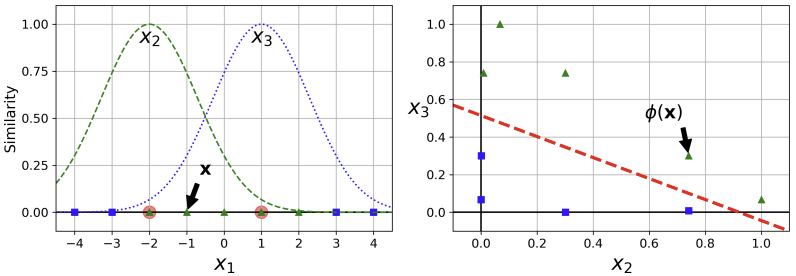
landmark는 어떻게 선택하는 걸까? 가장 간단한 방법은 데이터셋의 모든 instance에 랜드마크를 만드는 것이다. 이는 차원 수를 늘리며 데이터셋을 linearly seperable하게 만든다. 그런데 이는 학습셋의 크기가 피처의 수보다 큰 경우, 기존의 피처 수를 drop하고 학습셋 만큼의 새로운 피처를 만들기 때문에 피처의 수를 늘린다는 단점이 있다.
2-4) Gaussian RBF Kernel
polynomial kernel과 마찬가지로, 실제로 새로운 항을 추가하지는 않지만 그와 같은 효과를 내는 kernel trick이 similar function-RBF에도 존재한다. SVC의 하이퍼파라미터 kernel 를 rbf로 바꾸고, gamma를 지정해주면 된다.
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])아래 그림은 gamma()와 C 값을 다르게 하며 분류를 한 것이다. 가 커지면 종 모양의 곡선이 더 좁아지며, 각 instance가 미치는 영향이 줄어든다. 결정 경계선은 instance 주위에서 wiggle하며 고르지 못하게 된다. 반면 가 작아지면 종 모양 곡선은 더 넓어지며 각 instance가 미치는 영향의 범위가 커지고, 결정 경계선은 매끈하게 된다. C와 비슷하게 로도 규제를 할 수 있다는 것을 알 수 있다.
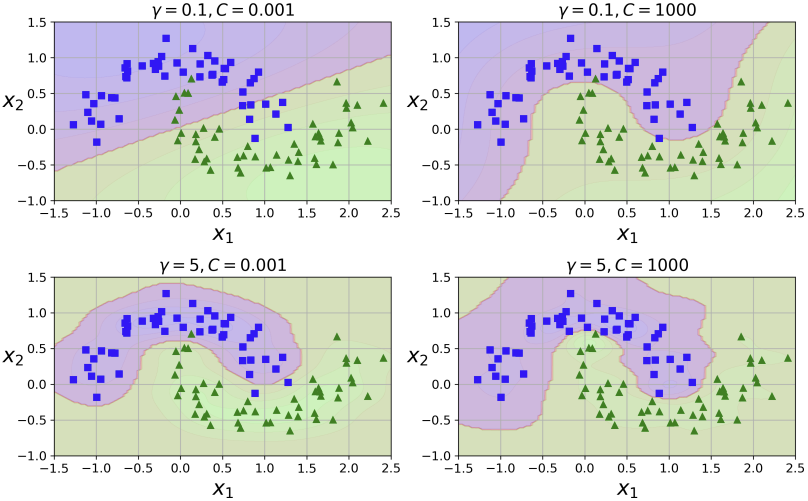
3) SVM Regression
svm regression의 목적은 classification과 반대이다. svm regression은 street 안에 데이터포인트들이 더 많도록 해야하고(= margin), street 밖의 데이터들로 인한 margin violation이 제한되어야 한다.
| 모델 | 목적 | |
|---|---|---|
| SVM Classification | street width를 크게, 데이터포인트들은 off the street이 되도록 | (street 안의) margin violation 최소화 |
| SVM Regression | street 안에 데이터포인트들이 많게 | (street 밖의) margin violation 최소화 |
street의 width은 으로 조절할 있다. epsilon이 크면 거리의 폭이 커지고, 작으면 거리의 폭 또한 작아진다.
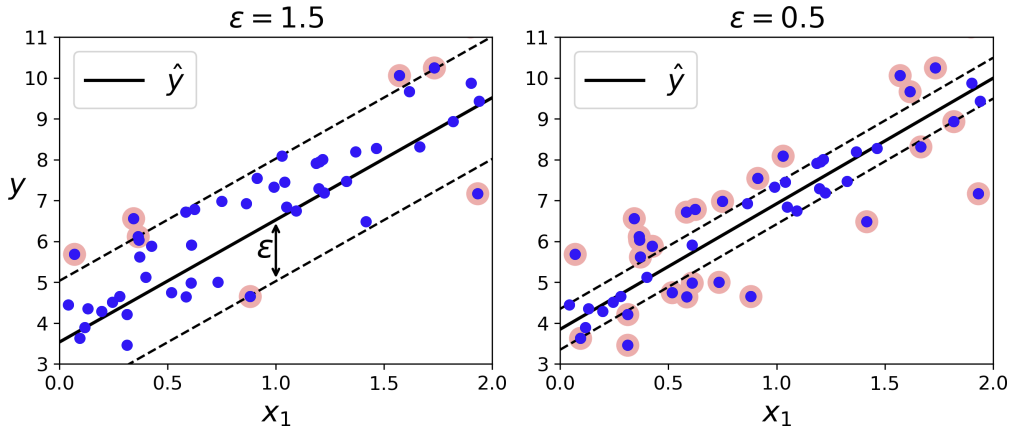
svm regression은 -insensitive (loss function)라고 불리는데, 그 이유는 svm regression에서는 예측값과 실제값의 차가 특정 임계값을 안 넘으면, 그 차이에 대해 모델이 패널티를 부과하지 않기 때문이다. 즉, 이내의 차이면 무시되고 그 데이터포인트는 모델의 성능에 영향을 미치지 않는다.
코드
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5)nonlinear regression의 경우, kernerlized SVM model을 사용할 수 있다. 아래 그림은 degree가 2인 polynomial kernel을 사용하여 quadratic set을 나타낸 것이다. 오른쪽 그림에서는 C의 값을 줄여서 규제를 가했다.

코드
- LinearSVC -> LinearSVR
- scales linearly with the size of the training set
- SVC -> SVR
- supports kernel trick
- gets too slow when the training set grows large
from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1)4) lecture ㅊㅊ
책에서는 "Under the hood"라는 이름으로 SVM의 더 깊은 내용을 다루기 시작한다. 그런데 개념 사이사이의 설명이 부족해서인지 내가 이해를 못해서인지는 몰라도 어쨌든 이해가 하나도 안돼서 인터넷을 열심히 검색해보았다. 결과적으로 SVM을 다룬 강의 하나를 찾았는데,"명강의"라는 말이 절로 나온다.. 이게 오픈소스로 되어있다는 게 MIT한테 너무 감사할 따름..
강의는 총 두 번 반복해서 들었다. 처음에는 책에 필기를 대충하며 들었고, 두번째에는 굿노트에 정리를 해가며 들었다. SVM을 수식적으로 접근해서 원리를 기반으로 이해할 수 있어서 좋은 것 같다. 그러나, 이 강의를 듣는다고 해서 (예로) similarity function의 원리와 같은 세세한 내용을 모두 알 수 없다는 건 알아뒀으면 한다. 나도 나중에 SVM의 새로운 내용을 접하게 된다면 그때가서 지식을 더 쌓으려고 한다. 한 번에 SVM을 정복하겠다는 생각은 좀 오만했던 것 같다ㅎㅎ
강의 필기는 아래에 공유하지만, 강의를 직접 들어보는 걸 ㅊㅊ한다!
강의 링크
https://www.youtube.com/watch?v=_PwhiWxHK8o
강의 필기
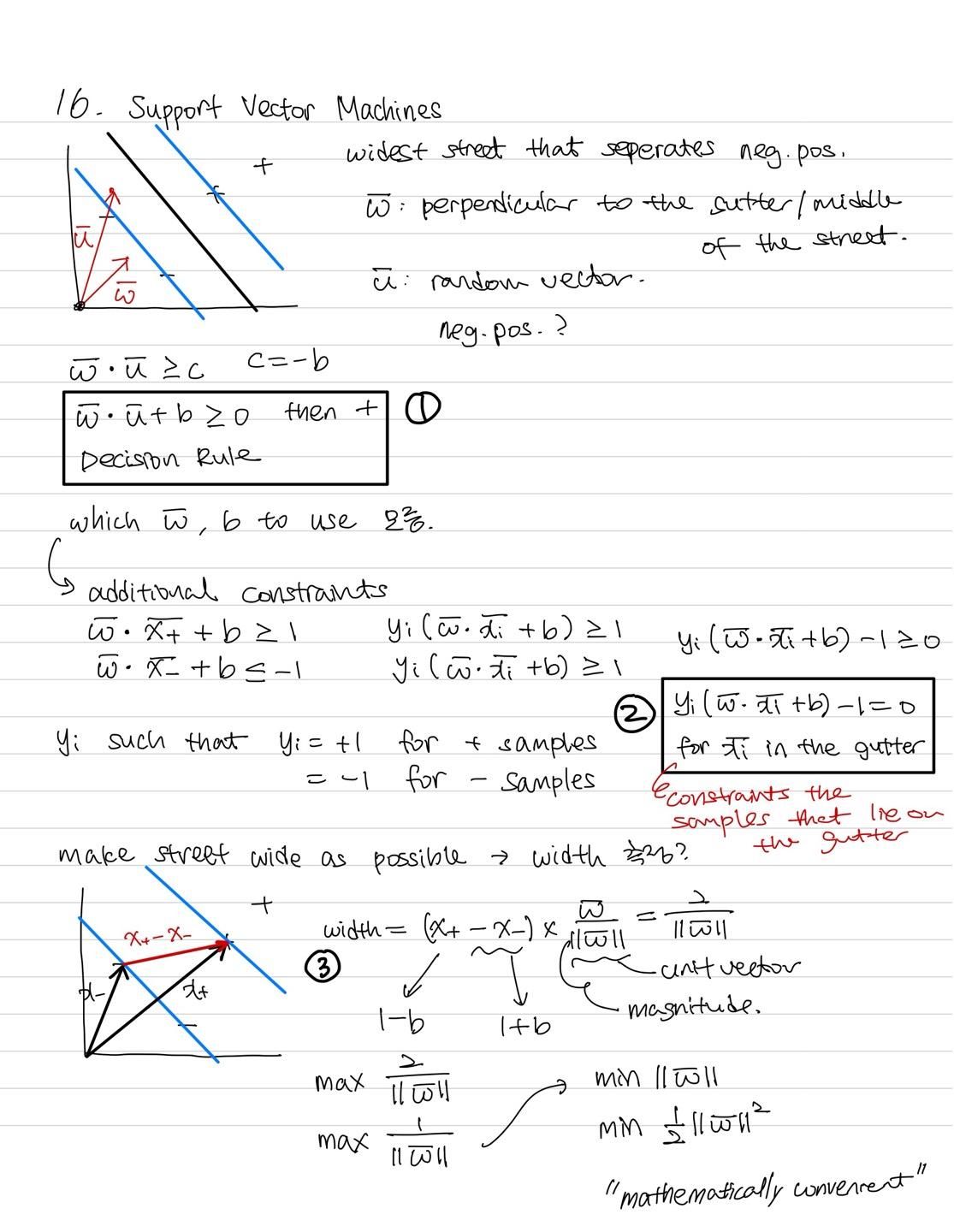


출처: Hands-On Machine Learning by Aurelien Geron