[ML] Polynomial Regression

shihyunlim·2024년 8월 17일

Machine Learning

목록 보기

7/20

1) Polynomial Regression

앞에서는 선형적인 형태의 데이터에 선형 회귀 모델을 적용하였다.

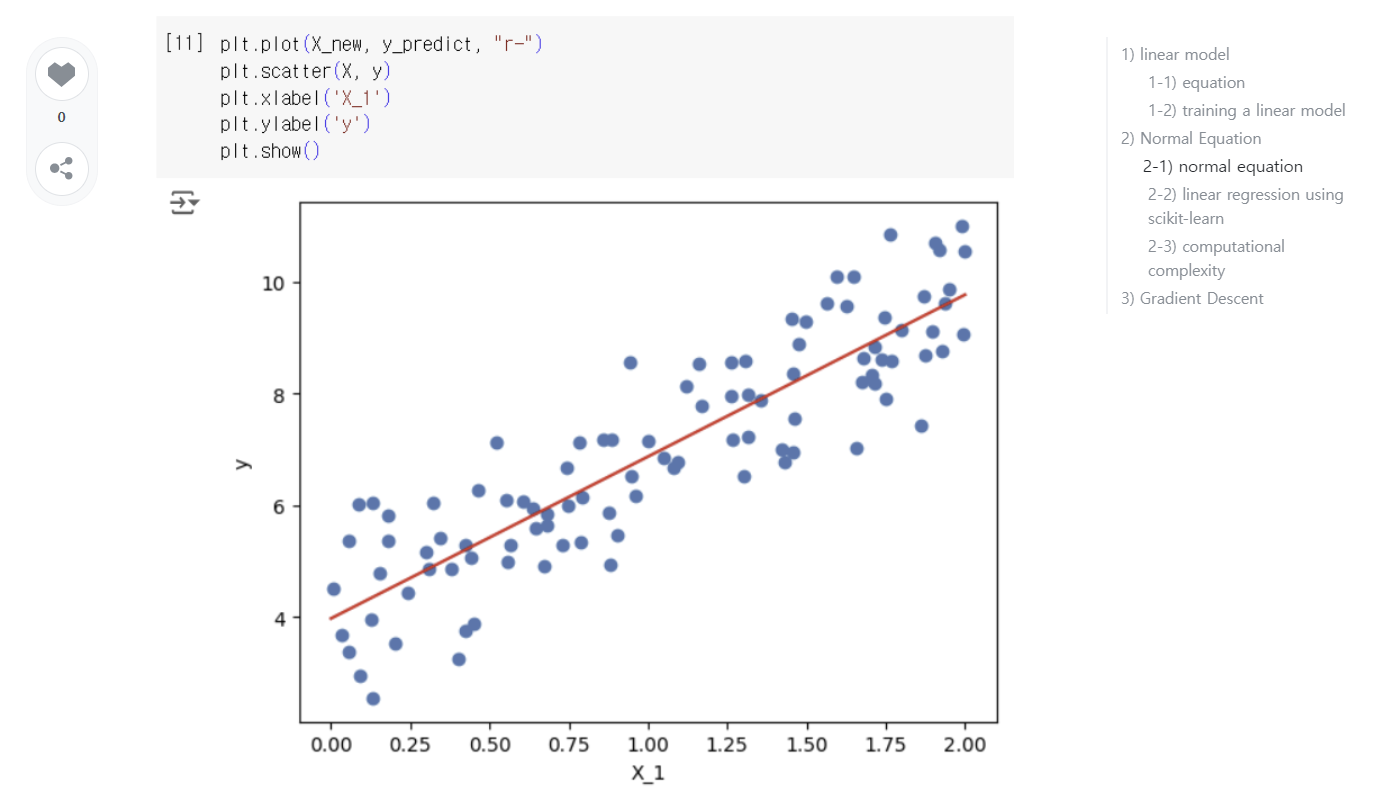
그렇다면 선형적이지 않은, 더 복잡한 형태의 데이터에 대해서는 어떻게 해야할까?

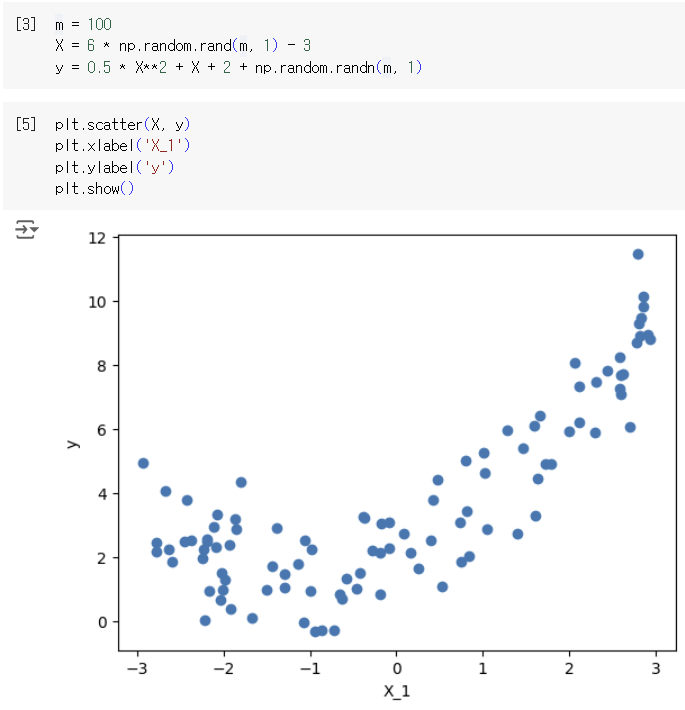
-> nonlinear data를 학습할 때에도 linear model을 사용할 수 있다. 대신, 데이터 feature들의 거듭제곱 항들을 추가해야 한다. 이 방법을 Polynomial Regression이라고 한다.

PolynomialFeatures(degree=n)는 특성이 n개인 배열을, 주어진 degree까지 특성 간의 모든 교차항을 추가하여 특성이 $\frac{(n+d)!}{d!n!}$ 개인 배열로 변환함. 이를 통해 다항 회귀는 특성 사이의 관계를 찾을 수 있음
*default degree는 2임

PolynomialFeatures 클래스는 fits_params라는 선택적 매개변수와 함께 X와 y에 맞게 transform되도록 학습하고, X의 transformed version을 반환함
*transformer: 데이터 변환을 수행하는 기계 학습 모델이나 도구

변환된 X (=X_poly) 확인 가능. degree=2로 설정하였으므로 X_poly[0]는 X[0]과 X[0]**2로 구성된다.

nonlinear 데이터에도 선형 회귀 모델을 이용할 수 있게 된다!

2) Learning Curves

위 데이터에 대해 1차 함수, 2차 함수, 300차(?) 함수를 그려 놓은 것이다. 보면 알겠지만 2차 함수가 이 데이터에는 가장 적합하다. 그런데 이 데이터를 만들 때부터 2차식을 이용했기 때문에 2차 함수가 가장 적합하다는 건 너무나도 당연하다.

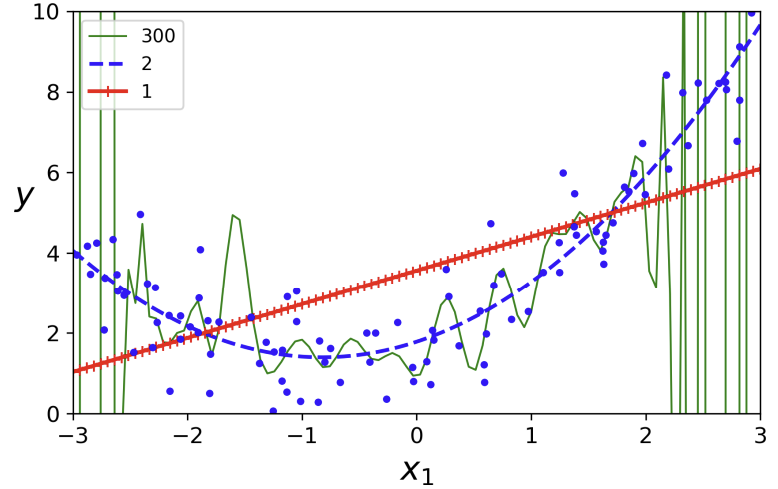
실제 데이터가 주어진다면 선형 모델의 차수를 이처럼 쉽게 구하기는 힘들 것이다. 그렇다면 모델의 복잡도는 어떻게 정하고, 그 모델이 overfitting 혹은 underfitting 한지 어떻게 판단할까?
-> 모델의 일반화 성능 확인
-> 방법은 두 가지가 있음. 첫번째는 cross validation을 이용하는 것, 두번째는 training set과 test set에 대한 모델의 성능을 나타낸 learning curves를 그려보는 것

2-1) cross validation

➡️cross validation

2-2) learning curves

학습 곡선은 모델의 훈련 오차와 검증 오차를 epoch의 함수로 나타낸 그래프임. 사이킷런의 learning_curve() 함수는 훈련 세트의 크기를 증가시키면서 모델을 재훈련하지만, 모델이 점진적인 학습을 지원하는 경우(partial_fit() 또는 warm_start 가능한 경우) learning_curve() 호출시 exploit_incremental_learning=True로 지정하면 모델을 점진적으로 훈련시킬 수 있음. 또한 이 함수는 훈련 세트의 크기, 훈련 세트의 점수, 검증 세트의 점수를 반환함

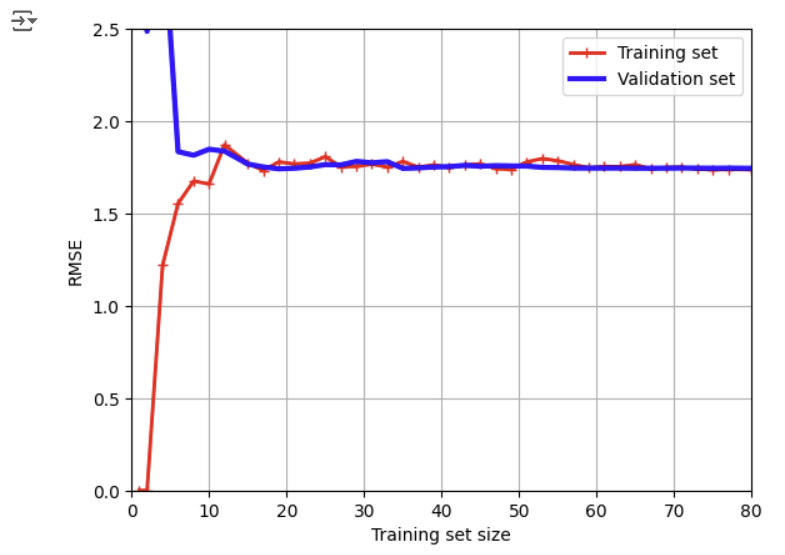
plain linear regression 모델(= a straight line)의 learning curves를 그린 것이다.

극초반에 학습셋의 오차가 0에 가까운 이유: 한두 개의 데이터에 대해서 선형 모델이 적합했기 때문
학습셋의 오차가 증가하다가 멈추는 이유: 학습 데이터를 더 넣는다고 하여 성능이 더 나아지거나 나빠지지 않기 때문
극초반에 검증셋의 오차가 매우 큰 이유: 모델이 한두 개의 데이터에만 적합하다보니, 일반화가 안되었기 때문에 새로운 데이터의 검증셋의 오차가 클 수밖에 없음
검증셋의 오차가 감소하다가 멈추는 이유: 모델이 새로운 데이터를 학습하면서 오차가 작아진다 싶더니, 새로운 데이터를 계속해서 넣어도 모델의 성능이 달라지지 않기 때문

-> 두 셋의 사이가 매우 가깝고, plateau에 도달하였으며, 오차값이 큰 이 경우는 underfitting model의 전형적인 형태이다.
-> underfitting을 해결하려면 더 복잡한 모델을 만들어야 한다.

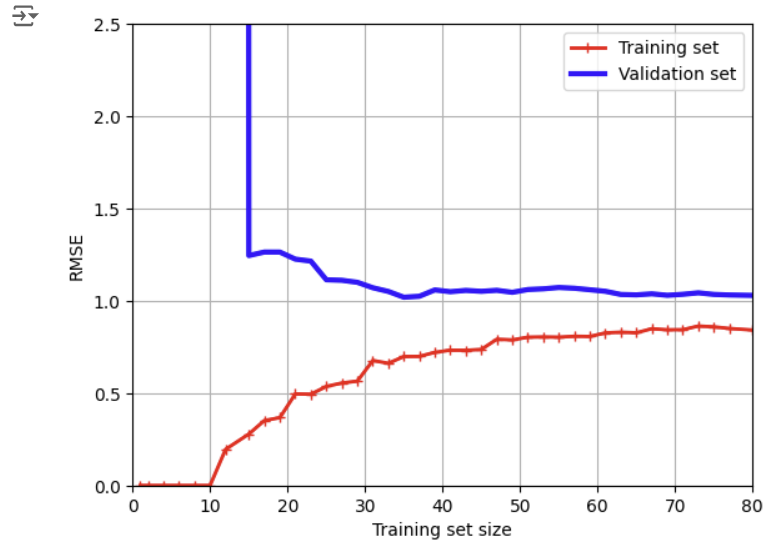
다음은 linear regression을 사용한 polynomial regression 모델의 learning curves를 그린 것이다.

학습셋의 오차가 매우 작아졌다. 차수가 높기 때문에 주어진 학습셋에 과도하게 잘 맞기 때문
(직접 작성한 코드의 결과로는 잘 안보이지만..ㅎ) 학습셋과 검증셋의 간격이 커졌다. 모델이 검증셋보다 학습셋에 잘 맞기 때문

-> 이런 형태의 그래프는 overfitting model의 전형적인 모습을 보여준다.
-> overfitting 문제를 해결하기 위해서는 검증 오류가 학습 오류에 도달할 때까지 학습 데이터를 더 넣어주거나, degree를 줄이면 된다.

*scikit learn의 pipeline은 여러 데이터 전처리 단계와 모델을 순차적으로 연결하여 하나의 객체로 처리할 수 있게 해주는 도구로, 코드의 간결성과 재사용성을 높임
➡️ 참고: 4-4) Transformation Pipelines

2-3) Bias-variance Trade-off

"모델의 일반화 오차는 세 가지 다른 종류의 오차의 합으로 표현될 수 있다."
-> 위에서 데이터에 맞는 모델 복잡도를 어떻게 찾는지, 과대적합과 과소적합을 어떻게 판단하는지에 대한 방법, 즉 데이터에 알맞는 일반화 성능이 좋은 모델을 찾는 방법으로 cross validation과 learning curve 그리기가 나왔음. 그리고 일반화 성능은 일반화 오차가 작을수록 좋을 것임
-> 이 얘기 나온 김에 일반화 오차에 대해 얘기하려는 것으로 보임