문제 링크
문제
티어: 골드 1
알고리즘: dp

입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. T는 1,000보다 작거나 같은 자연수이다. 각 테스트 케이스는 정수 하나로 이루어져 있다. 이 정수는 문제에서 설명한 타일의 너비 N이다. N은 자연수이다.
N은 타일을 채우는 경우의 수가 2,147,483,647 이하이도록 주어진다.
출력
각 테스트 케이스에 대해 4*N크기의 타일을 채우는 방법의 경우의 수를 출력한다.
풀이
4 * N 크기의 타일을 채우는 방법의 경우의 수를 출력해야 한다.
4 x 2 크기의 타일에서 가로를 1 늘려준 4 x 3 크기의 타일을 구한다면 4 x 2에 오른쪽에 4 x 1이 추가된 형태일 것이다.
그러면 이 추가된 타일을 채우는 경우의 수는 다음과 같다.
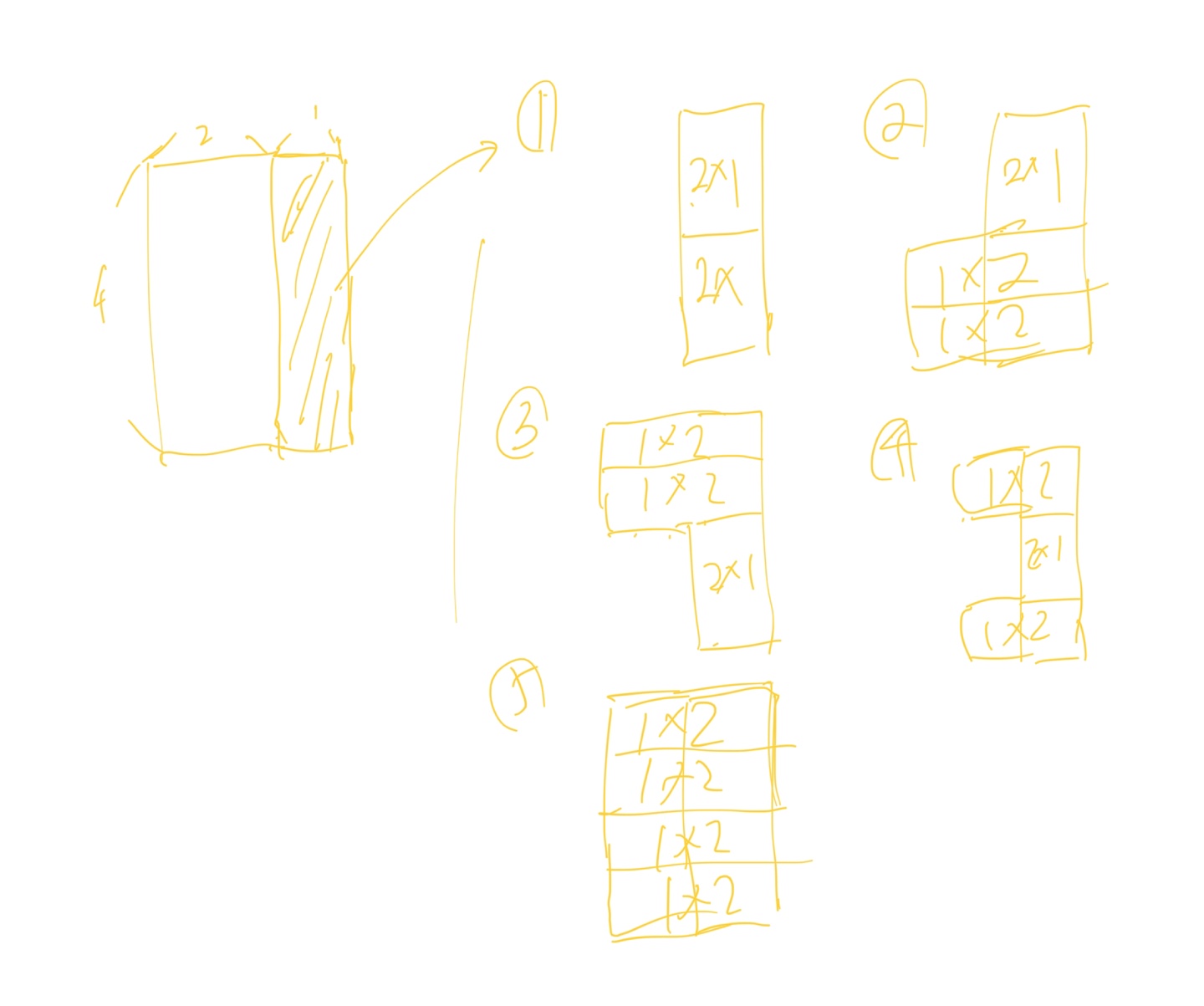
이렇게 다섯 가지의 경우가 존재하고, 2번과 3번은 뒤집으면 같은 경우이기 때문에 묶어서 생각하면 된다.
각 경우의 수를 결합해보면 다음과 같은 모양들이 필요함을 알 수 있다.
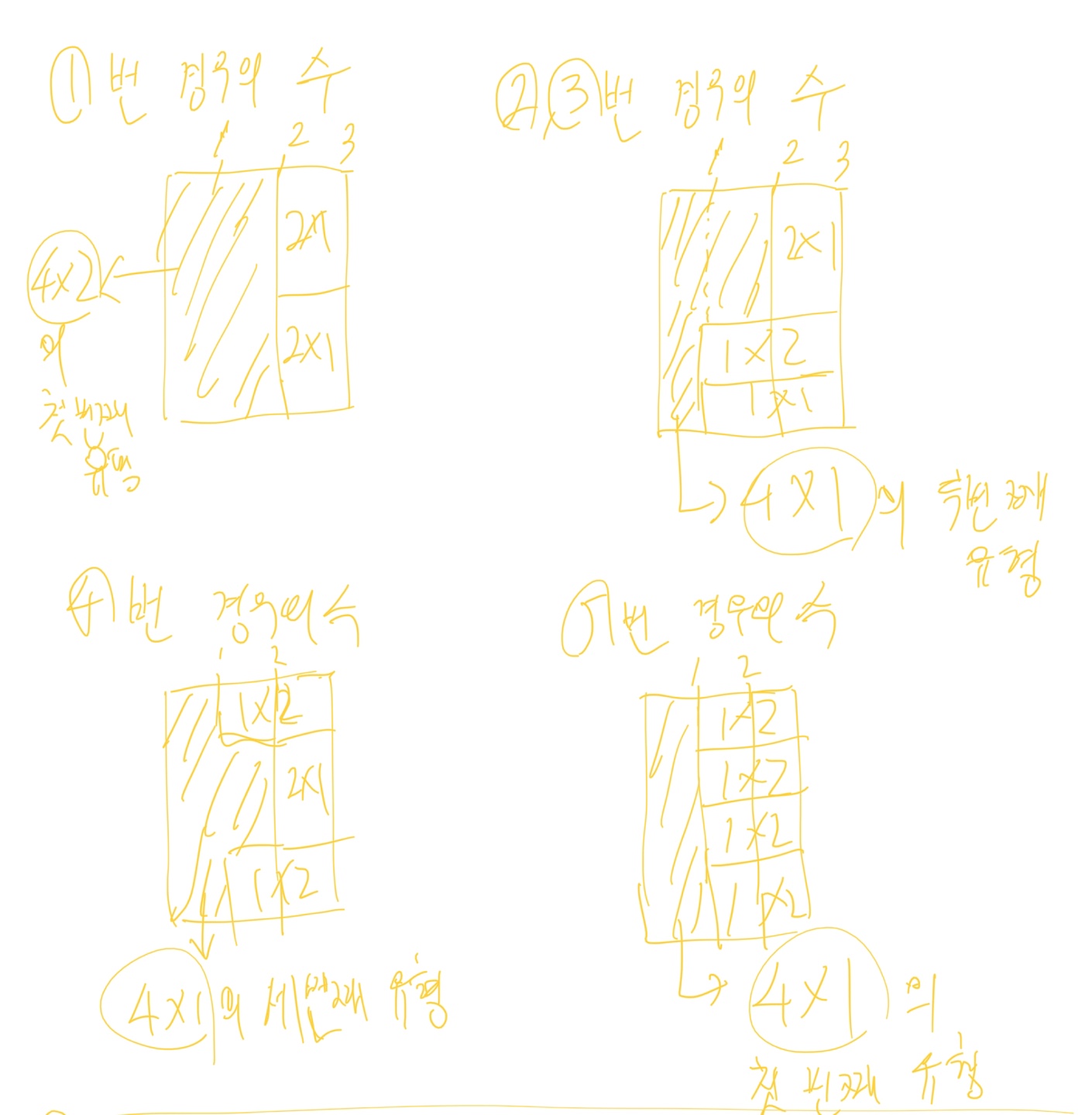
그래서 (4 x 가로 길이) 마다 다음과 같은 세 가지 타입을 계산해 놓으면 다음 (4 x (가로 길이 + 1))를 구할 수 있다.
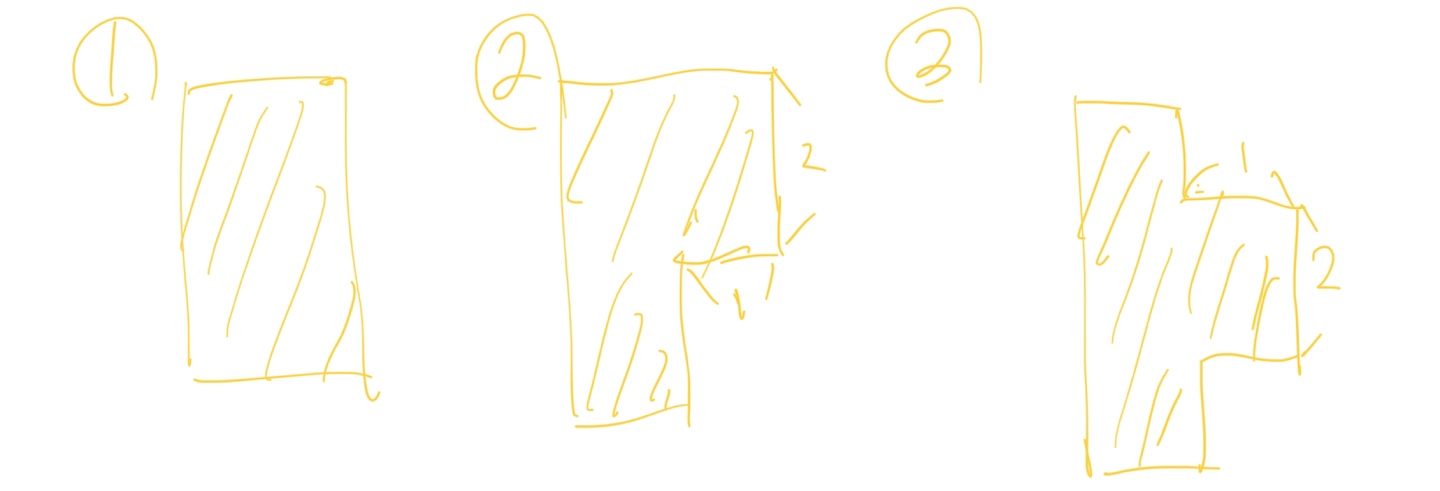
그러면 이 세 가지 타입을 구하려면 어떻게 해야될까?
첫 번째 타입은 앞에서 말했듯이 5가지 경우의 합이다.
두 번째 타입은 다음과 같이 구할 수 있다.
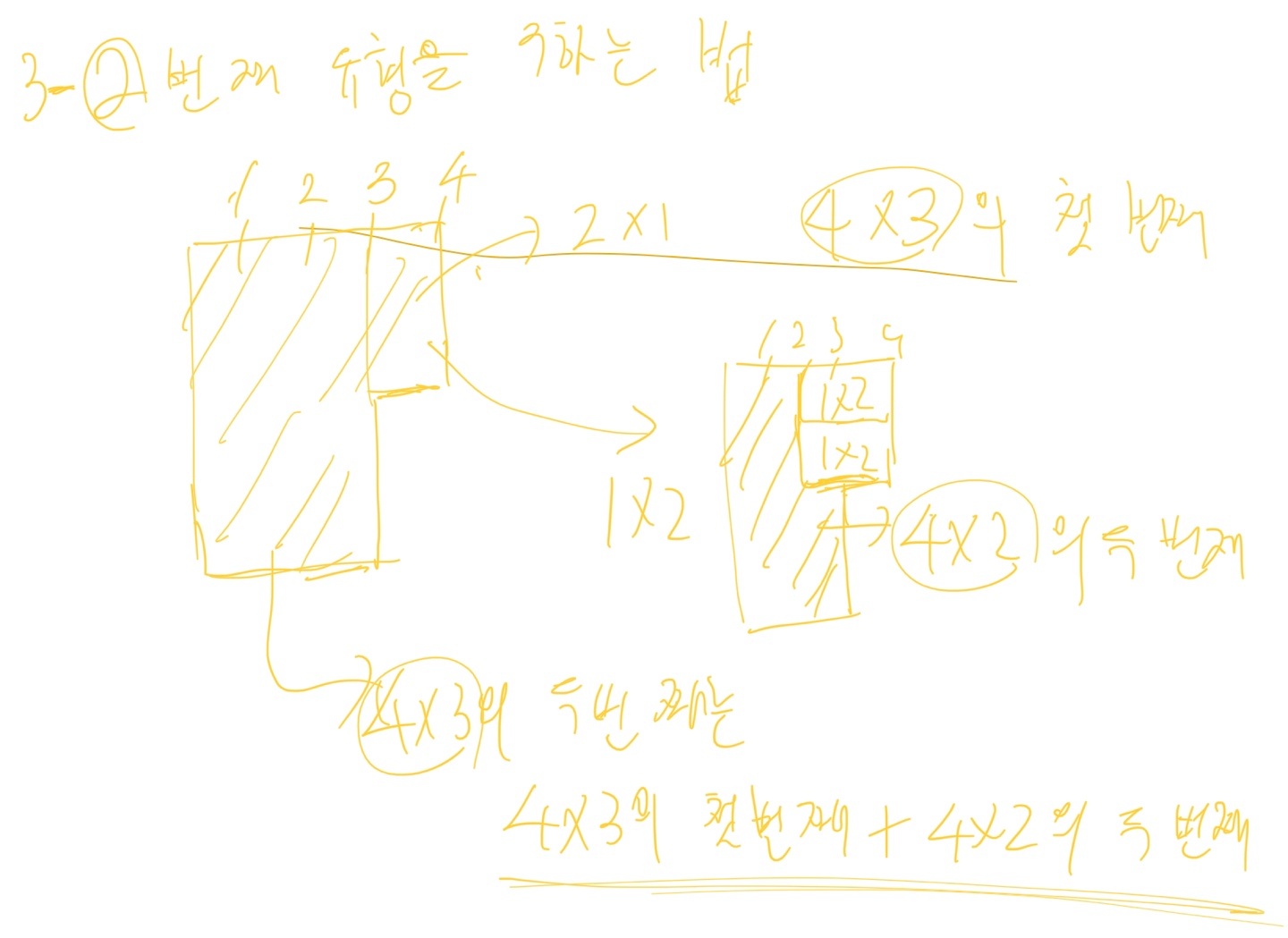
세 번째 타입은 다음과 같이 구할 수 있다.
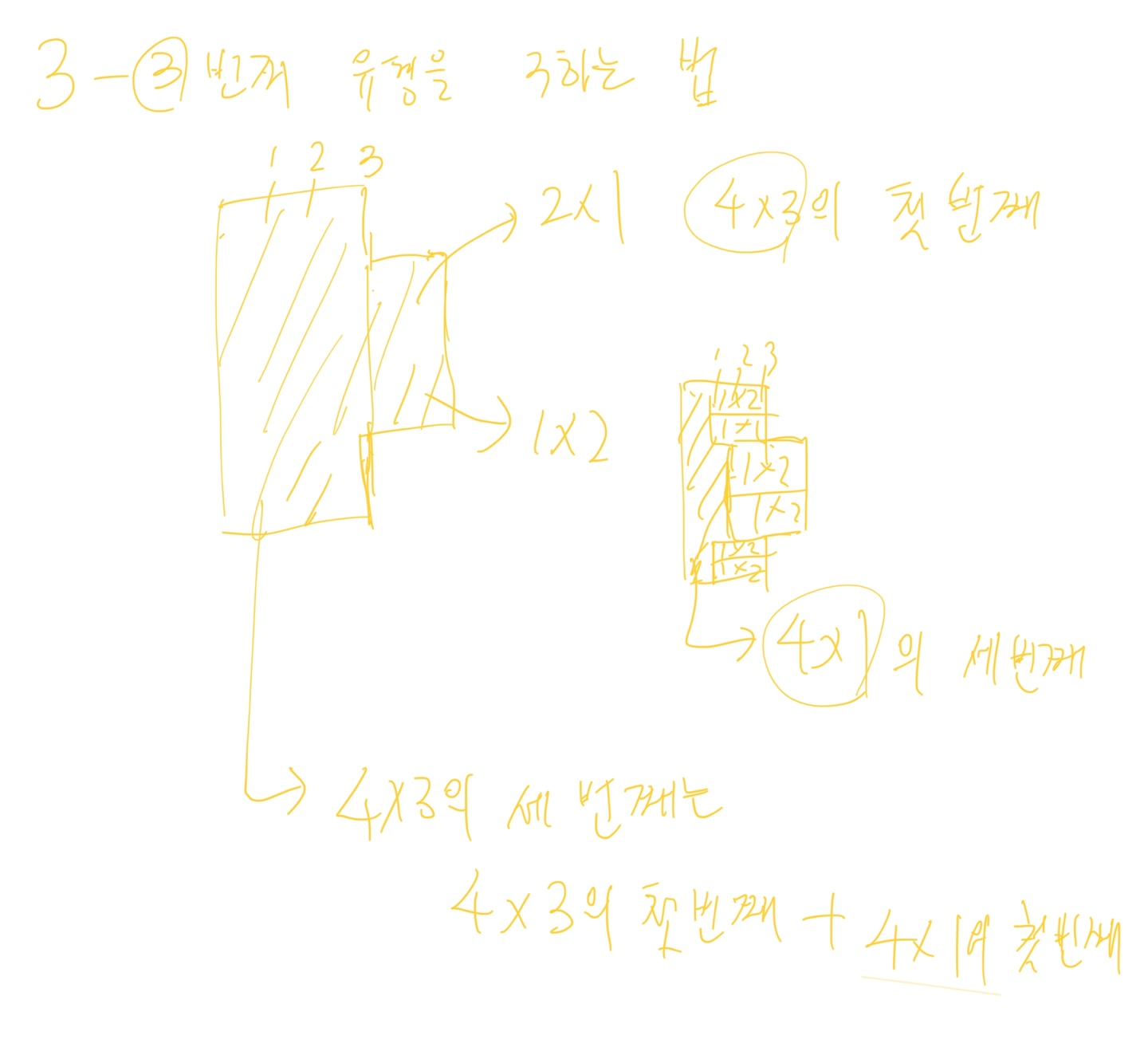
이를 토대로 dp를 정의하면 [A][B]는
A -> 가로 길이
B -> 첫 번째, 두 번째, 세 번째 타입
정의할 수 있다.
그래서 4 * 3부터 구한다고 했을 때 일반화하면 다음과 같은 점화식이 도출된다.
- 첫 번째 유형 dp[i][0] = dp[i - 1][0] + (dp[i - 2][1] * 2) + dp[i - 2][2] + dp[i - 2][0];
- 두 번째 유형 dp[i][1] = dp[i][0] + dp[i - 1][1];
- 세 번째 유형 dp[i][2] = dp[i][0] + dp[i - 2][2];
이 풀이의 시간 복잡도는 O(N)이다.
소스 코드
import java.io.*;
import java.io.*;
public class Main {
static int T;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
T = Integer.parseInt(br.readLine());
int[][] dp = new int[31][3];
fillDp(dp);
StringBuilder sb = new StringBuilder();
for(int t=0; t<T; t++) {
int N = Integer.parseInt(br.readLine());
sb.append(dp[N][0]).append("\n");
}
System.out.println(sb.toString());
}
static void fillDp(int[][] dp) {
dp[1][0] = 1;
dp[1][1] = 2;
dp[1][2] = 1;
dp[2][0] = 5;
dp[2][1] = 7;
dp[2][2] = 6;
for(int i=3; i<dp.length; i++) {
dp[i][0] = dp[i - 1][0] + (dp[i - 2][1] * 2) + dp[i - 2][2] + dp[i - 2][0];
dp[i][1] = dp[i][0] + dp[i - 1][1];
dp[i][2] = dp[i][0] + dp[i - 2][2];
}
}
}회고
처음 풀 때 정리를 안하면서 풀다 보니까 헷갈려서 다시 돌아가고 풀고를 반복해서 시간이 오래 걸렸다.
문제점을 인식하고, 하나 하나 정리해가며 푸니 빠르게 점화식을 도출할 수 있었다.
그래서 문제를 풀 때 정리해가며 푸는 습관을 꼭 들여야겠다.