SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers

KeyPoints:

- Positional encodeing free hierarchically structured Transformer encoder
(resolution independent test/training performance, multiscale features)
- Simple structured MLP decoder

Backgrounds

• Former works are concentrated on encoders only (PVT, Swin Transformers, etc).
• Still requires high computation on decoders.

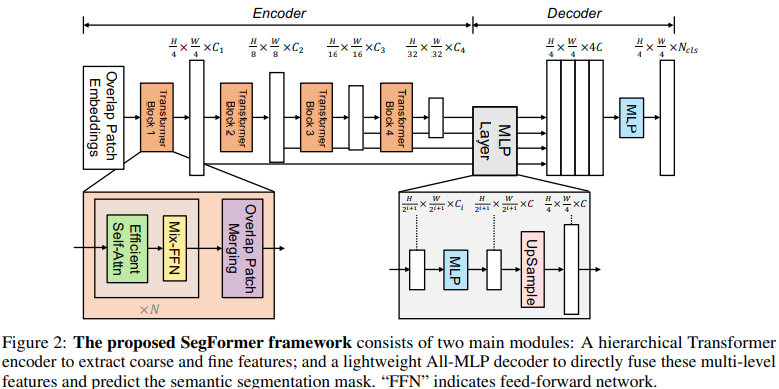
Overal Method

1. Input image(H×W×3) is divided in to patches of size 4×4.
2. By hierarchicl Transformer encoder, mulit-level features sized {1/4,1/8,1/16,1/32} of the original image, are obtained from the patches.
3. Pass the features to ALL-MLP decoder and get $\frac{H}{4}\times\frac{W}{4}\times N_{cls}$ resolution segmentation mask prediction. ($N_{cls}$ : num of categories)
   

Overlapped patch merging.

1. Like ViT unified N×N×3 patches to 1×1×C vectors, heirarchical features from $\frac{H}{4}\times\frac{W}{4}\times C_i$ are shrinked into $\frac{H}{8}\times\frac{W}{8}\times C_{i+1}$. And method iterates for other heirarchy.
   (Note. What ViT paper actually did was flattening $p\times p\times3$ patches into $1\times p^2c$ vectors.
   Dividing H×W×3 images into N patches size $p \times p$ and flatten those patches into $N\times P^2C$.)
2. To preserve local continuity among the patches, K = 7, S = 4, P = 3 (and K = 3, S = 2, P = 1) is set, where K is the patch size, S is the stride, P is the padding size.

Efficient Self-Attention.

By reducing lenth of sequence $K$(size N$\times$C) from N to $N\over R$ with
$\hat{K}$ = Reshape($N\over R$ , C · R)($K$) [reshape N$\times$C to $N\over R$$\times$(C · R)]
$K$ = Linear(C · R , C)($\hat{K}$ ) [linear transpose $N\over R$$\times$(C · R) to $N\over R$$\times$C]
the self-attension mechanism complexity decreased from $O(N^2)$ to $O({N\over R}^2)$

Mix-FFN.