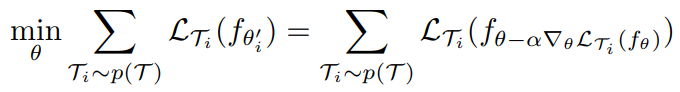1. Introduction

 Proposing general and model-agnostic meta-learning algorithm.

2. Model-Agnostic Meta-Learning(MAML)

 2.1. Meta learning scenario

  Meta-training part

1. A task $T_{i}$ is drawn from task distribution $p(T)$.
2. With $T_i$, the model is trained with only $K$ samples and feedback from $L_i$.
3. Tested on new samples from $T_i$ , this test error is considered when imporving model f(generaly expressed as 'model f' since meta-learnable object is differ from algorithms to parameters) with respect to the parameters.(Thus this test error serves as training error.)

  Meta-testing part

1. New tasks are sampled from $p(T)$, and meta-performance is measured after learning from K samples.(Tasks used for meta-testing are out held out during meta-training)

2.2. A Model-Agnostic Meta-Learning Algorithm

 Intuition

• Some representations are more transferable.
  -> Let Neural networks learn features from such representations, thus broadly applicable to all tasks.

 Problems

1. Existence of such representations.(Personal question)
2. How can we tell which one is the one.

 Approach

1. It is a relative matter. Not looking for an absolute transferable, but relatively more transferable representation.
2. By finding the model that makes most rapid adjustment on new tasks from $p(T)$. Thus able to evoke a large improvement from a small change. More transferable.

Setup

• $\mathcal{T_i}\sim p(\mathcal{T})$ : distribution of tasks
• $\mathcal{T}_i$ : batch of tasks, $\mathcal{T}_i = \{\tau_1,\cdots,\tau_i\}$
• $\tau_m$ : single task, $\tau_m = \{x_m^j,y_m^j\}_{j=1}^{J}$

 Algorithm

Inner loop

• For all $\mathcal{T_i}=\{\tau_1,\cdots,\tau_i\}$, sample K data points $\mathcal{D}^s$ each and compute gradient descent.
  • $\theta_i' = \theta - \alpha\nabla_\theta\mathcal{L}_{\mathcal{T_i}}(f_\theta)$
• Get $i$ number of inner loop parameters
• Sample $\mathcal{D}^q$ for meta update (outer loop)
• For each task $\tau_m$, we have $\theta_m',\mathcal{D}_m^q$ where $m = \{1,\cdots,i\}$

Outer loop

• For each tasks $\tau_m$, compute $\mathcal{L}_m(f_{\theta'},\mathcal{D}^q)$
• Compute gradient descent with sum of all losses.
  • $\theta \leftarrow \theta-\beta\nabla_\theta\displaystyle\sum_{\mathcal{T_i\sim P(\mathcal{T})}}\mathcal{L}_{\mathcal{T_i}}(f_{\theta'_{i}})$
  • Note that, since $\theta_i' = \theta - \alpha\nabla_\theta\mathcal{L}_{\mathcal{T_i}}(f_\theta)$, $\theta$ is driven with 2nd order differentiation.

    Concequently, the meta-object is as follows:

Meta test step (Meta performance test)

• Sample batch of task $\mathcal{T}_i^* \sim p(\mathcal{T})/\mathcal{T}_i$
• Test it on full algorithm
  • Purpose of the model includes training.

3. Species of MAML

 3-1. Supervised Regression and Classification

  MSE for regression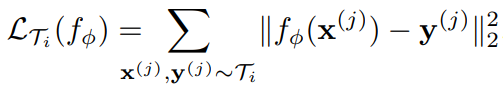

  CE-loss for classification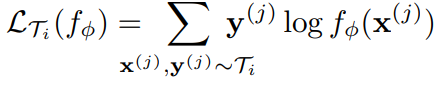  

  MAML for Few-Shot Supervised Learning

• Note that, K-shot classification tasks use K input/output pairs from each class, thus NK data points for N-way classification.

3.2.Reinforcement Learning

  Definitions

1. $T$ = { $L(x_{1}, a_{1}, . . . , x_{H}, a_{H}), q(x_{1}), q(x_{t+1}|x_{t}, a_{t}), H$ }
   $T$ : Task (Each learning problems)
2. $L(x_{t},a_{t})$ : Loss function with observation $x_{t}$, output $a_{t}$
3. $q(x_{t})$ : A distribution of initial observations
4. $q(x_{t+1}|x_{t}, a_{t})$ : A transition distribution
5. $H$ : An episode length. A cycle length of generating an output of a query set. (Each time $t$, model generates samples of length H by chooosing an output $a_{t}$)

 Algorithm

Terminology

• task : (Classification for example) Each work given specific classes to perform classification, where this specific classes may not include whole class range. Thus, there might be more than one tasks under one dataset.