Ian Goodfellow의 Deep Learning을 보고 정리한 글

Probability and Information Theory

AI에서 확률 이론은 두 가지 방법으로 사용된다.

1. 확률의 공식들이 AI system이 어떻게 추론을 해야하는지 알려준다. 그러므로 우리는 우리의 알고리즘이 확률 이론으로부터 나온 식을 계산하거나 추측하도록 설계한다.
2. AI system의 행동을 이론적으로 분석하는데 사용될 수 있다.

반면에 정보 이론은 이러한 확률 분포에서 불확실도를 양적으로 측정할 수 있도록 해준다.

Probability

확률은 어떤 사건이 일어날 가능성을 의미한다. 확률이라는 개념은 관점에 따라 다를 수 있다. 예를 들어 반복되는 사건의 발생 빈도수를 측정해서 (e.g. 동전 던지기나 주시위 던지기) 확률 값을 계산하는 경우, 우리는 frequentist probability의 관점에서 확률을 본다. 반면에 반복되는 사건이 아니고 의사가 환자에게 암에 걸릴 확률이 30%라고 말하는 경우를 생각해보면, 이는 반복되는 사건이 아니다. 이럴 때 우리는 확률을 어떠한 믿음의 정도 또는 지식의 정도를 표현하기 위해 사용하는데, 이를 bayesian probability라고 한다.

Random Variable

Random variable이란, 랜덤하게 서로 다른 값을 받을 수 있는 변수를 말한다. 즉, 결과가 확률적으로 정해지는 변수를 말한다. 이는 discrete할수도, continuous할 수도 있다. 심지어 확률 변수는 numerical value가 아닌 그냥 named state일 수도 있다.

Probability Distribution

Probability distribution은 random variable 또는 random variable의 집합이 가능한 state에 대해 어떻게 분포하는 지를 의미한다. 즉, 확률변수가 특정 값을 가질 확률을 나타내는 함수가 된다.

우리는 어떤 사건을 예측하기 위하여 해당 사건의 확률을 계산하게 된다. 그 확률 값을 구하기 위해서는 확률 분포를 알아야하고, 머신러닝의 학습 과정이 곧 확률 분포를 알아내는 과정이라고 이해할 수 있다.

Discrete Variables and Probability Mass Functions

discrete variable에 대한 확률 분포는 probability mass function을 이용해 표현된다. $P(X)$에서 $P(x)$값이 1이라는 것은 $X=x$가 확실하다는 뜻이고, 0이라는 것은 불가능하다는 것이다.

probability mass function은 여러 변수에 대해서 동시에 표현할 수도 있는데, 이를 joint probability distribution이라고 한다. $P(X=x, Y=y)$는 $X=x$이고, $Y=y$일 확률을 의미한다.

probability mass function $P$는 다음의 특징을 만족해야한다.

• $P$의 도메인은 $X$의 모든 가능한 state의 집합이다
• $\forall x \in X, 0 \le P(x) \le 1$
• $\sum_xP(x)=1$

예를 들어 $k$개의 서로 다른 state를 갖는 random variable $x$의 uniform distribution를 생각해보면 probability mass function은 다음과 같이 설정할 수 있다.

Continuous Variables and Probability Density Functions

continuous random variable을 다룰 때에는 probability density function(PDF)를 사용하고 다음과 같은 특징을 만족해야한다.

• $P$의 도메인은 $X$의 모든 가능한 state의 집합이다
• $\forall x \in X, p(x)\ge 0$ : $p(x)\le 1$의 조건이 사라졌습니다.
• $\int_xp(x)dx=1$

probability density function $p(x)$는 그 값 자체로 확률이 되는 것은 아니고, volume $\delta x$에 대해서 $p(x)\delta x$로 주어진다.

즉, univariate example에서, $x$가 $[a,b]$안에 있을 확률은 $\int_{[a,b]}p(x)dx$로 구할 수 있다.

예를 들어 $[a,b]$ 사이에서 정의되는 uniform distribution을 생각해보면 probability density function은 다음과 같이 설정할 수 있다.

Marginal Probability

만약 어떠한 변수들의 집합으로 이루어진 확률 분포를 알고 있을때, 그 중 하나의 변수에 대해서만 확률 분포가 필요할 수 있다. 이 subset에 대한 확률 분포를 marginal probability라고 한다.

예를 들어, $x$와 $y$의 discrete random variable로 이루어진 $P(x,y)$를 알고 있다고 하면, $P(x)$는 다음과 같이 구할 수 있다.

만약 $x$와 $y$의 각 값을 row와 col로 하는 grid table을 생각하면, $x$에 대한 marginal probability를 구할 경우, 쉽게 각 row를 summation하여 구할 수 있다고 생각하면 된다.

Conditional Probability

많은 경우, 다른 사건이 발생한 상황에서 어떤 사건의 확률을 구하는 것이 중요하다. 이는 conditional probability라고 한다.

$X=x$일때, $Y=y$일 조건부 확률은 $P(Y=y|X=x)$라고 쓰며 다음과 같이 계산된다.

이 값은 $P(X=x)\gt0$에서만 정의되며, 절대 일어나지 않을 사건에 대한 조건부확률은 구할 수 없다.

The Chain Rule of Conditional Probabilities

여러 random variables로 이루어진 joint probability distribution은 하나의 variable에 대한 conditional distribution으로 분해될 수 있다.

이러한 성질을 확률의 chain rule 또는 product rule이라고 부른다.

쉽게 이해하기 위해 먼저 $P(x,y)$를 생각해보자.

이는 $x$와 $y$의 연속된 시행을 의미하는데, $y$가 먼저 발생하고 $x$가 그다음으로 발생했다고 생각하면 $P(x,y)=P(y)*P(x|y)$로 쉽게 표현할 수 있을 것이다.

그리고 이는 conditional probability 공식 그자체와 부합한다.

그대로 3가지 변수로 확장을 시켜보자.

$P(x,y,z)$는 $y,z$가 발생했을 때, $x$가 발생한 것으로 생각할 수 있다. $P(y,z)$는 $z$가 발생했을 때, $y$가 발생한 확률로 생각할 수 있으므로 아래의 공식을 간단히 유도할 수 있다.

Independence and Conditional Independence

$x$와 $y$의 joint distribution이 다음과 같이 표현될 수 있다면, $x$와 $y$의 random variable은 independent하다고 한다.

또한 random variable z가 주어진 상황에서 다음과 같이 표현될 수 있다면, $x$와 $y$는 conditionally independent하다고 한다.

Expectation, Variance and Covariance

확률분포 $P(x)$에 관한 함수 $f(x)$의 expectation 혹은 expected value는 $P$로부터 나온 $x$를 $f$가 받았을 때 평균 값을 의미한다.

이산 확률 변수에 대해서는

연속 확률 변수에 대해서는

expectation은 linear하기 때문에 다음의 성질을 갖는다.

Variance는 random variable $x$의 함수 값이 서로 다른 $x$값에 따라 얼마나 변하는지를 나타낸다.

분산이 작다면 $f(x)$값은 expected value 주변으로 모이게 된다. 분산의 제곱근은 standard deviation이라고 한다.

Covariance는 두 값이 얼마나 선형적으로 연관있는가를 나타낸다.

covariance가 크다면 두 값이 함께 크게 변한다는 것을 의미하는데, 양수의 covariance는 한 변수가 증가할 때, 다른 변수도 함께 증가하는 것을 의미하며, 음수의 covariance는 한 변수가 증가할 때, 다른 변수는 감소하는 것을 의미한다.

공분산과 독립의 개념은 비슷하지만, 엄연히 다르다.

두 변수가 서로 독립이면 공분산은 0이지만, 공분산이 0이라고 모두 독립인 것은 아니다.

공분산은 선형 관계에 대한 의존성을 의미하므로, 공분산이 0이라는 것은 선형관계가 없다는 것을 의미할 뿐이지만, 독립은 모든 관계가 없다는 것을 의미하므로 독립이 더 큰 범주라고 생각할 수 있다.

예를 들어 $y=x^2$의 함수를 생각해보면 $x$와 $y$는 서로 선형이 아니므로 $cov(x,y)$는 0이지만, 여전히 $x, y$는 관계가 있다.

Common Probability Distribution

여기서는 machine learning에서 주로 사용되는 간단한 확률 분포를 간단히 알아보자.

Bernoulli Distribution

베르누이 분포는 하나의 binary random variable(0 혹은 1의 결과만 존재하는)만 있는 분포이다.

그리고 단 하나의 parameter $\phi \in [0,1]$로 조절된다.

$\phi$값은 random variable이 1의 값을 가질 확률을 의미한다.

1이 나올 확률 그 자체가 확률 변수 $X$의 기댓값이 되는 것을 볼 수 있습니다.

Gaussian Distribution

분포 중 가장 유명하고 널리 쓰이는 분포로, normal distribution 혹은 gaussian distribution으로 불린다.

$\mu \in R$과 $\sigma \in (0,\infty)$의 두 parameter가 이 분포를 결정한다.

이 두 parameter는 확률 변수 $X$의 mean, standard deviation을 의미한다.

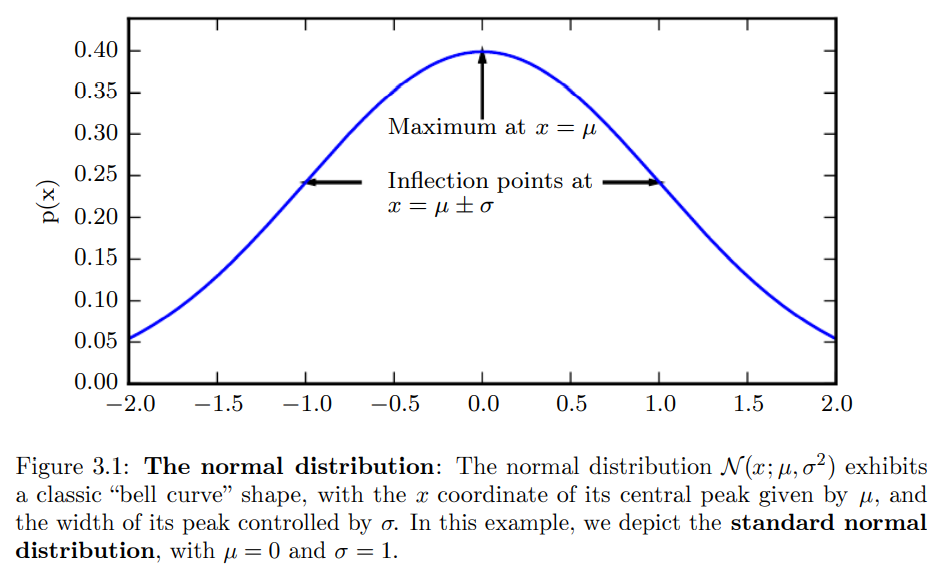
정규 분포는 거의 모든 곳에 사용될 수 있다. 어떤 변수에 대한 사전 정보가 없다면 보통 정규 분포를 채택하는 것이 좋은 선택일 수 있다.

Central limit theorem에 의하면 동일한 확률 분포를 가진 독립 확률 변수 n개의 평균의 분포는 n이 크다면 정규분포에 가까워 진다.

이 말은 실제로 많은 복잡한 시스템은 데이터만 많아지면 단순히 normal distribution으로 근사할 수 있다는 것으로 해석할 수도 있다.

정규 분포는 다변수로 확장이 가능하며 이를 multivariate normal distribution이라고 한다.

Exponential and Laplace Distribution

deep learning을 사용할 때, 가끔 $x=0$에서 sharp point를 갖는 distribution이 필요할 때가 있다.

이를 위해 사용하는 것이 exponential distribtution이다.

exponential distribution은 $1_{x\ge0}$의 indicatior function을 사용하여 negative $x$의 확률을 0로 지정한다.

Useful Properties of Common Functions

여기서는 deep learning model에 사용되는 확률분포를 다룰 때 자주 등장하는 function들에 대해서 알아보자.

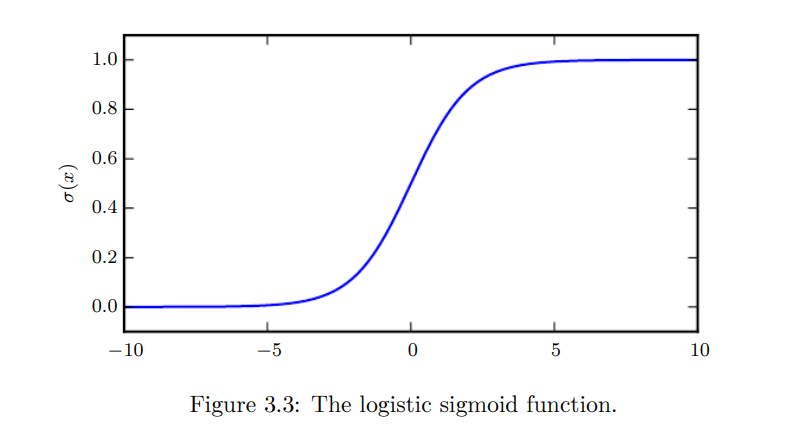
먼저 logistic sigmoid function이 있다.

이 함수는 범위가 $(0,1)$이기 때문에 Bernoulli distribution에서 $\phi$ parameter를 만들어내는데 많이 사용된다.

sigmoid function은 argument의 값이 positive로 매우 커지거나 negative로 매우 커지면 값을 saturate시키므로 input의 작은 변화에 insensitive하다.

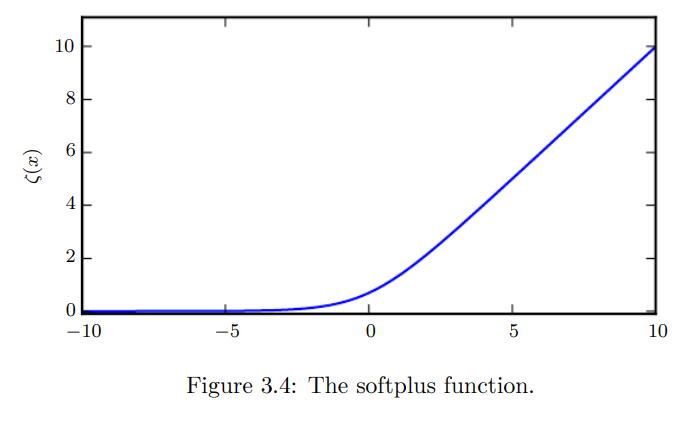
또 다른 함수는 softplus 함수이다.

이 함수는 범위가 $(0,\infty)$이기 때문에 normal distribution에서 $\beta$나 $\sigma$값을 만들어내는데 사용된다. 이 이름 자체는 이 함수가 $x^{+} = max(0,x)$의 soft 버전이기 때문이다.