Ian Goodfellow의 Deep Learning을 보고 정리한 글
개인적인 공부도 포함
출처: 서울대학교 컴퓨터 개론 및 실습

기계학습이라는 것은 통계학에 기초를 두고 있고, generalization, underfitting 그리고 overfitting을 이해하는데 parameter estimation, bias, variance 등의 개념은 매우 중요하다.

Mitchell(1997)
“A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience."

즉, 머신 러닝에서 learning이라 함은 experience (data)를 이용하여 어떤 task를 수행하는데 있어서 performance가 증가하는 것을 의미한다.

우리는 현실 세계의 데이터(input)와 각 데이터에 대응되는 현상(label)에 대한 관계(function)를 찾으려한다.

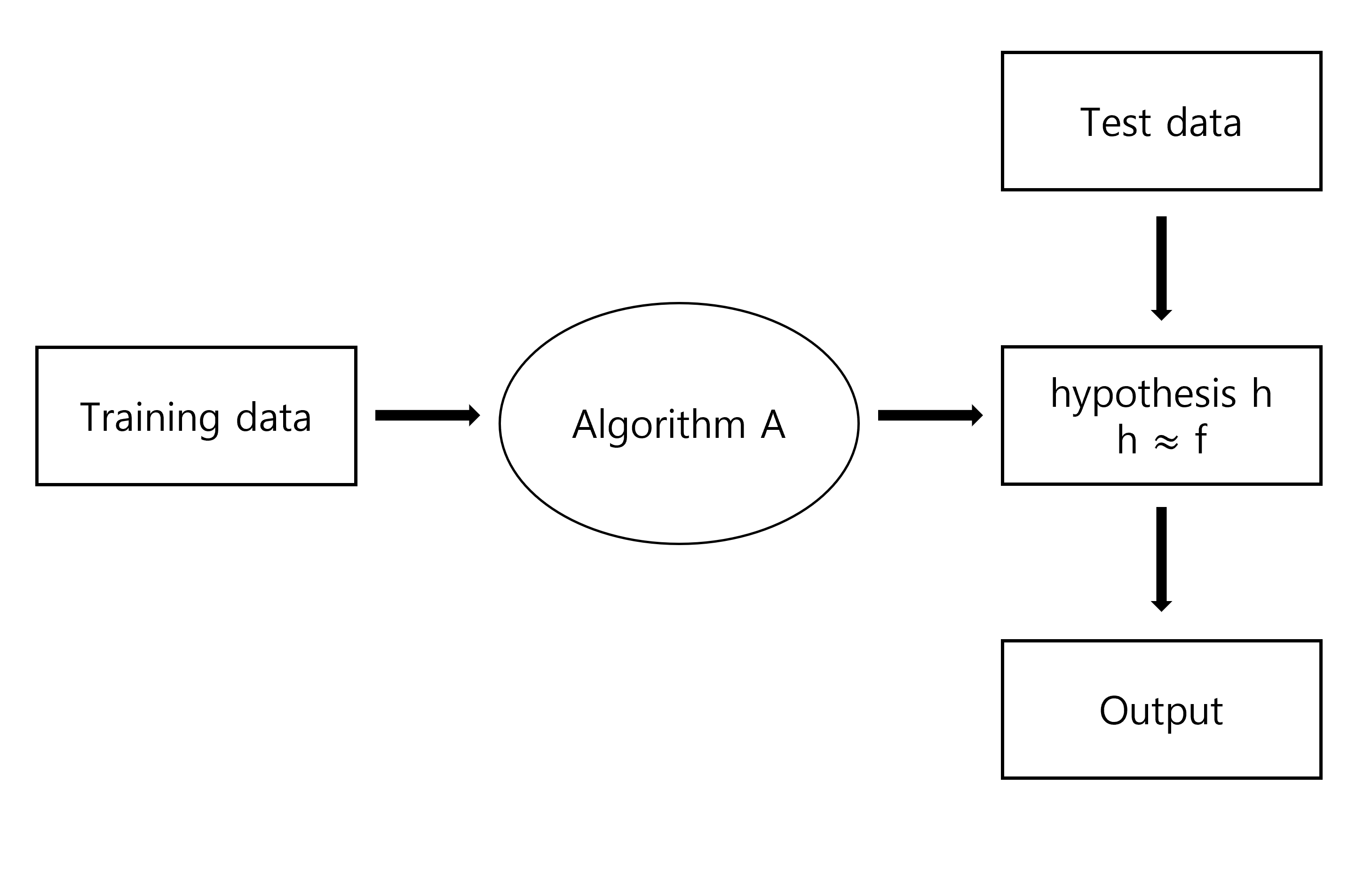
머신 러닝에서는 training data를 이용하여 어떤 알고리즘을 통해 hypothesis를 만들어낸다.

이 hypothesis 함수 $h$는 실제 데이터와 그 현상의 관계를 설명하는 unknown target function $f$를 추정하여 최대한 주어진 데이터를 잘 설명하고자 한다.

가장 중요한 포인트는 주어진 데이터를 가장 잘 설명할 수 있는, unknown function $f$와 가장 비슷한 결과를 내는, $f$의 추정값 $h$를 찾아내는 것이다.

확률의 관점에서 머신러닝은 주어진 데이터를 가장 잘 설명할 수 있는 확률 분포를 찾는 과정으로 생각할 수 있다.

이 과정은 적절한 확률 분포를 가정하고, 이 확률분포의 parameter를 유추하는 과정을 말한다.

예를 들어 주어진 데이터가 정규분포로부터 나왔다고 가정한다면, 우리는 추출된 데이터를 가장 잘 설명할 수 있는 mean과 variance를 찾아내면 되는 것이다.

Estimators, Bias and Variance

Point Estimation

point estimation은 내가 추정하고자 하는 값에 대해 단 하나의 최고의 예측 값을 찾는 것이다.

이는 single parameter가 될 수도, vector가 될수도 있다.

${x^{(1)},...,x^{(m)}}$을 m개의 independent and identically distributed(i.i.d.) data points라고 하면, point estimator 혹은 statistic은 이 데이터의 어떤 함수이다.

좋은 estimator는 실제 값 $\theta$에 최대한 가깝게 내는 함수이다.

하지만 실제로 $\theta$는 알 방법이 없다.

지금부터 true parameter value $\theta$는 고정되어 있지만 알 수 없고, point estimate $\hat\theta$는 데이터에 대한 함수라고 하자.

데이터가 랜덤하게 뽑히기 때문에 추정량 $\hat\theta$ 또한 확률 변수이다.

Bias

Estimator의 bias는 다음과 같이 정의된다.

기댓값은 데이터에서의 기댓값을 의미하고 $\theta$는 데이터 생성 분포를 정의하는 참값을 의미하므로 bias는 예측값 - 실제값으로 이해할 수 있다.

Variance and Standard Error

Variance는 trainind set이 바뀔 때, 모델이 얼마나 변동하는지를 나타내는 값이다.

standard error는 이의 square root 값이다.

즉, 데이터를 resample할 때마다 추정 값이 얼마나 바뀌냐를 의미한다.

샘플에 따라 추정값이 너무 많이 변한다면 좋은 estimator가 아닐 수도 있다.

Trading off Bias and Variance to Minimize Mean Squared Error

데이터 셋 $D = [(x_1,y_1),..., (x_n,y_n)]$이 어떤 distribution $P$로부터 주어졌다고 하자. 그리고 하나의 $x$에 대해 $y$값이 다양할 수 있다고 가정하자.

예를 들어 $x$가 집이고 $y$가 집 값이면, 같은 집 $x$에 대해서 가격이 다르게 책정될 수도 있는 것이다.

• Expected Label (given $x\in R^d$ ) : 주어진 x에 대해 y의 기댓값이다.

  $\tilde y(x)=E_{y|x}[Y]=\int_yyPr(y|x)\partial y$

• Hypothesis : machine learning algorithm A가 dataset D를 통해 배운 것; 데이터셋 D를 이용하여 학습된 모델;

  $h_D =A(D)$

• Expected Test Error (given $h_D$) : 특정 데이터에 따른 예측값과 참값의 오차

  $E_{(x,y)\sim P}[(h_D(x)-y)^2] = \int_x\int_y(h_D(x)-y)^2Pr(x,y)\partial y\partial x$

• Expected Classifier (Given algorithm A) : 알고리즘에 의한 기댓값; 모든 possible dataset으로 학습된 모델의 평균값;

  $\tilde h = E_{D\sim P^n}[h_D]=\int_Dh_DPr(D)\partial D$

• Expected Test Error (Given algorithm A) : 데이터 기반 학습값과 참값의 오차

  $E_{(x,y)\sim P, D \sim P^n}[(h_D(x)-y)^2] = \int_D\int_x\int_y(h_D(x)-y)^2Pr(x,y)Pr(D)\partial y\partial x \partial D$

여기서 $D$는 training points (training dataset)를 의미하고 $(x,y)$는 test points (test dataset)를 의미한다.

이 마지막의 expected test error를 한번 분해해보자.

가운데 term은 정리하면 0이 된다. (쉽게 생각하면 $h_D$의 평균이 $\tilde{h}$이기 때문에)

위에서 우항 첫번째 term은 variance가 된다. 즉, 데이터에 따라 모델의 출력이 변동하는 정도를 나타낸다.

두번째 항을 더욱 분해해보면,

여기서 우항 첫번째 항은 bias, 두번째 항은 noise를 의미하고, 마지막 항은 정리하면 0이 된다.

여기서 Bias는 모델의 출력값과 참값의 차이를 의미한다.

결론적으로 우리는 expected Test error를 다음과 같이 분해할 수 있게 된다.

그림으로 보면 다음과 같이 이해할 수 있다. (모델이 선형인 경우)

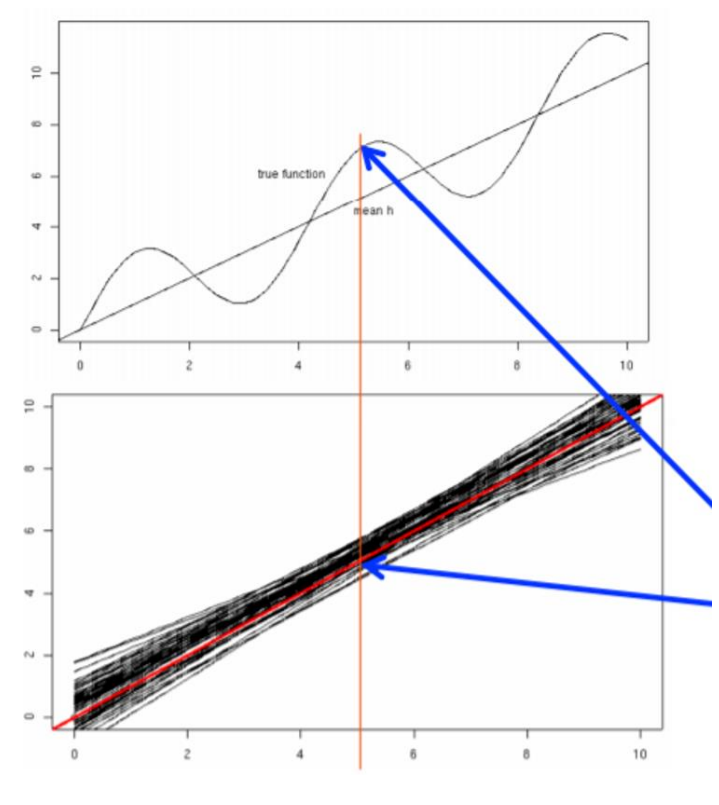
위의 그림에서 선형 모델을 가정하였으므로 검은색 선이 학습된 모델 $h_D$이라고 하자.

이 여러 개의 모델들이 하나의 데이터 포인트 $x$에 대해 내는 출력의 평균을 구할 수 있고 이 값이 알고리즘에 의한 기댓값 $\tilde{h}$이라고 생각할 수 있다.

이 prediction의 변동을 variance라고 하고, true value와 mean prediction의 차이를 bias, true value가 가지는 피할 수 없는 오류를 noise라고 한다.

아래 그림은 $x=5$일 때의 prediction 값을 따로 plot한 것으로, x축이 prediction, y축은 prediction의 확률값이다.

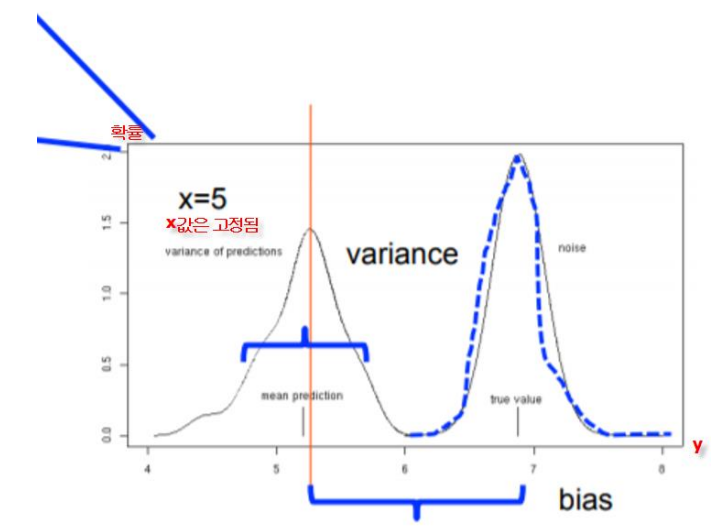
이를 통해 우리는 total error가 최소가 되는 적정선을 찾아야 한다.

Maximum Likelihood Estimation

다시 한번 말하자면 estimator는 데이터로 정의되는, 혹은 학습되는 함수라고 할 수 있으며, 우리는 이를 통해 $\theta$를 추정하고자 한다.

여기서 $\theta$는 실제 값으로도 생각해도 되고, 실제 값을 낼 수 있는 parameter로도 생각해도 된다.

추정량 $\hat\theta$는 실제 데이터 분포로부터 추출된 데이터를 설명하는 함수로, 좋은 estimator는 실제 값 $\theta$와 가까운 결과를 만들어내는 함수이다.

그러면 이 estimator 함수를 어떻게 얻어낼 수 있을까?

Maximum Likelihood Estimation은 parameter $\theta = (\theta_1, ...,\theta_m)$으로 구성된 확률밀도함수 $P(x|\theta)$에서 관측된 표본 데이터 집합에서 이 parameter를 추정하는 방법이라고 할 수 있다.

maximum likelihood estiamtor $\theta$는 다음과 같이 정의된다.

즉, 각 데이터 샘플에서 우리가 후보로 지정한 확률 분포 $p_{model}$에 대한 likelihood를 구해 모두 곱한 값을 최대화하여 우리가 얻은 데이터를 가장 잘 설명할 수 있는 확률 분포를 얻어내는 것이다.

아래에 그림에서도 초록색 분포보다는 노란색 분포가 추출된 data를 잘 설명한다고 할 수 있다.

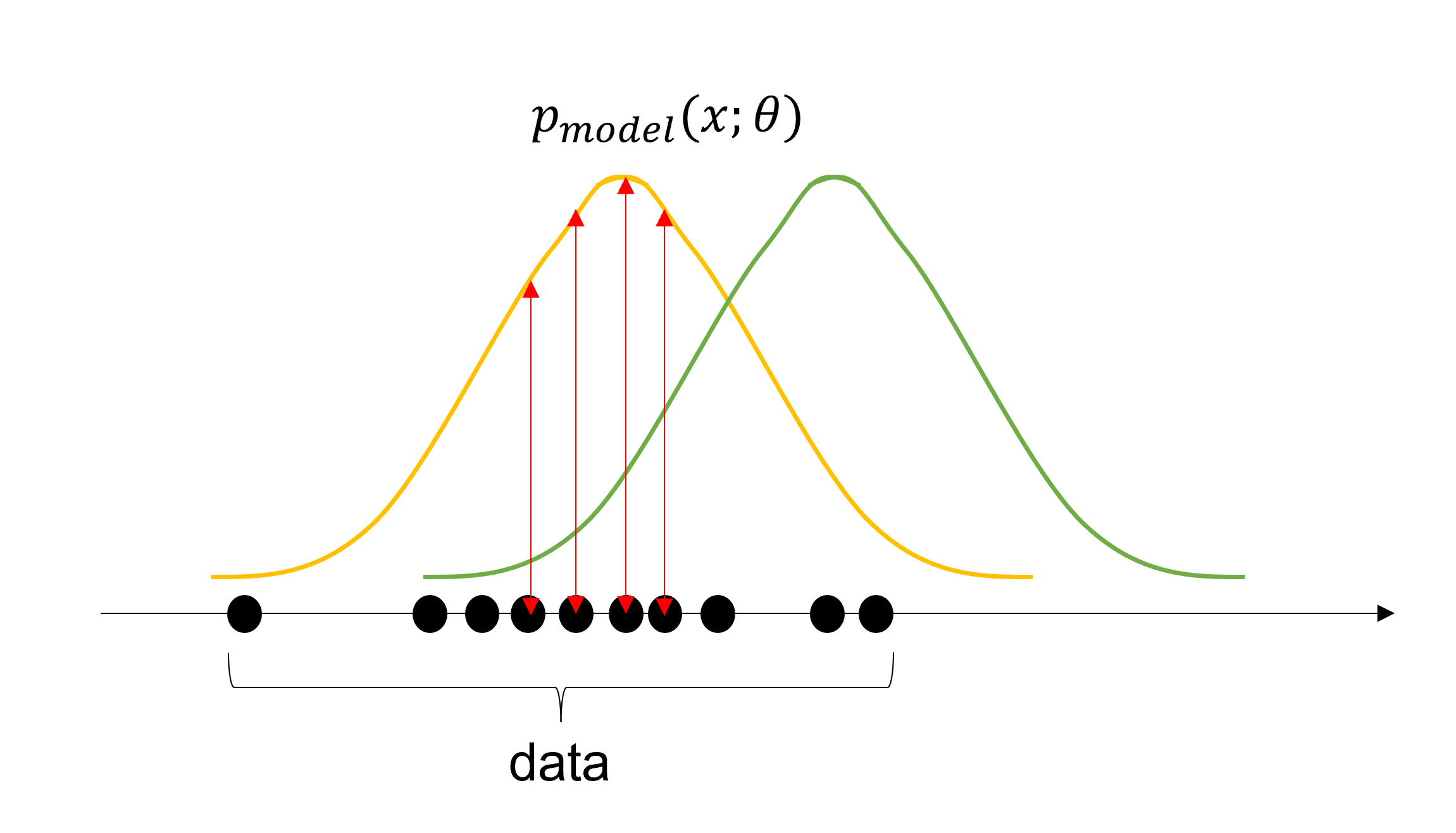
하지만 곱연산을 반복해서 계산하는 것은 쉽게 복잡해지기 때문에 연산의 편의성을 위해 보통은 log를 사용하여 합연산으로 바꾸어 사용한다.

또한 argmax를 하는 입장에서 합이나 평균이나 마찬가지이기 때문에 평균으로도 사용한다.

이러한 추정 방법을 바라보는 또 다른 관점 중 하나는 training set으로 정의되는 경험적인 분포 $\hat p_{data}$와 model이 만들어내는 분포의 차이를 줄이는 과정이라는 것이다.

이러한 정도를 나타내는 값이 KL divergence이다.

위의 식에서 $log\hat p_{data}(x)$는 사실 data generation process의 함수이므로 model을 학습시킬 때에는 아래의 항만 최소화시키면 된다.

그런데 이 값은 바로 위에 maximization 식과 완전히 똑같다.

결과적으로 KL Divergence를 최소화 시키는 것은 두 분포의 cross entropy를 최소화하는 것과 완전히 동일하다.

또한 KL Divergence는 최소 값이 0이므로 maximum likelihood를 minimum KL divergence로 보는 관점은 최적화 측면에서 유리하다.

Maximum likelihood는 가장 간단하고 효과적인 parameter estimation method가 맞다.

하지만 이 방법은 하나의 parameter에 대해서 주어진 training 데이터의 likelihood를 최대화하도록 하므로, 주어진 training data에 민감하다.

즉, 적은 training data에서는 overfitting이 일어나기 쉽다.

Bayesian Statistics

지금까지 위에서 다루었던 내용은 모두 frequentist statistics이다.

이 관점에서 우리는 하나의 고정되었지만 알 수 없는 true parameter $\theta$를 가정하고 (즉, 모집단은 변하지 않는 대상으로 여겨짐) 주어진 data를 이용하여 random variable인 $\hat \theta$를 추정한다.

그리고 그 결과가 타당하다고 판단되면 이 추정값을 사용한다. $\to$ 하나의 parameter가 정해짐.

통계학의 또 다른 관점인 Bayesian statistics에서는 반대로 가능한 모든 $\theta$를 고려한다.

모집단은 고정된 것이 아니고 확률 변수처럼 취급되며, 사전 정보로부터, 즉, 매 표본으로부터 나온 데이터를 새로운 출발점으로 사용한다. $\to$ parameter 자체가 확률적으로 예측된다.

이는 기본적으로 하나의 사건에서 믿음의 정도를 확률로 나타내는 베이즈 확률론에 기반한다.

헷갈릴 수 있지만, 베이즈 정리는 시나리오 측면에서 결과를 보고 원인을 찾는다고 생각할 수 있다. (단, 원인에 따른 결과는 사전에 알고 있다)

예를 들어, 길거리가 물에 젖어있는 것을 보고 이것이 비가 와서 그런것 인지, 물차가 지나가서 그런것 인지, 확률적으로 원인을 구한다.

이 개념을 이용한 parameter estimation 방법을 Maximum Posteriori Estimation(MAP)라고 한다.

이 방법은 $\theta$가 주어지고, 이 $\theta$에 대한 데이터의 확률을 최대화하는 것이 아니라, 주어진 데이터에 대해 최대 확률을 가지는 $\theta$를 찾는 것이다.

---

간단한 예시를 들어 MLE와 MAP의 차이를 이해해보자.

앞과 뒷면만 나올 수 있는 동전 던지기의 예제를 생각해보자. 10번을 던졌는데, 나온 결과는 다음과 같다.

H,T,T,H,H,H,T,T,T,T

$n_h$개의 앞면과 $n_t$개의 뒷면이 나왔다.
직관적으로 우리는 앞면이 나올 확률이 다음과 같다는 것을 알 수 있다.

이를 한번 유도해보자.

1. Maximum Likelihood Estimation

$P(H) = \theta$로 가정하자. 하지만 $\theta$ (parameter)는 알 수 없고, 우리가 가진 것은 오직 dataset($D$)이다.

$\theta$를 추정하기 위해 할 수 있는 방법으로 MLE를 생각할 수 있다.

우리는 먼저 $P(D|\theta)$를 모델링하기 위해 앞면 (H)가 나올 분포를 가정해야하고, binomial distribution이 쓸만할 것 같다.

위의 식을 미분해서 0이 되도록하는 paramter $\theta$를 찾으면 다음과 같은 결과를 얻을 수 있다.

• 여기서 알 수 있듯이 MLE는 우리가 관측한 data를 잘 설명해준다.
• 만약 n이 크고 모델 혹은 분포를 잘 가정했다면 (Hypothesis가 true model을 포함한다면), MLE는 true parameter를 잘 찾아준다
• 하지만, n이 작으면 MLE는 쉽게 overfitting될 수 있다.
• 또한 분포를 잘 가정해주지 않으면 MLE는 잘못된 parameter를 찾기 쉽다.

2. Maximum Posteriori Estimation

Prior knowledge가 있는 상황에서 동전을 던지는 상황을 생각해보자.

$\theta'$가 0.5에 가깝다는 직감이 있는 상황을 가정하자.

하지만 sample size가 너무 작아서 이 예측값을 믿을 수는 없다.

$\theta$가 0.5 결과가 나올 수 있도록 가상의 m번 던지기를 시행하면 추정 파라미터는 다음과 같다.

n이 클 때, 이는 큰 차이가 없지만, n이 작을 때 위 추정값은 나의 "prior belief"를 반영한다.

조금 더 제대로 유도해보자.

Bayesian way에서는 model $\theta$를 $P(\theta)$라는 분포로부터 추출한 random variable로 생각한다.

그러면 우리는 Bayes Rule로 인해 다음과 같이 쓸 수 있다.

• $P(D|\theta)$는 parameter $\theta$가 주어졌을 때 data의 likelihood
• $P(\theta)$는 parameter $\theta$의 prior distribution
• $P(\theta | D)$는 parameter $\theta$의 posterior distribution

D는 결과나 관측, $\theta$는 원인이라고 생각해도 무방하다.

이제, 아까 우리가 적절한 parameter로 0.5를 골랐던 것 처럼, 우리의 모델 $\theta$의 prior distribution $P(\theta)$로 beta distribution을 가진다고 생각하자.

beta distribution은 $\alpha$와 $\beta$값을 통해 $[0,1]$사이의 범위에서 정의되는 함수이므로 확률의 분포로 적합하다.

우리 모델의 parameter인 $\theta$의 분포를 가지고 있으니 $\theta$를 한번 추론해보자.

MAP의 원리는 posterier distribution $P(\theta|D)$를 maximize하는 $\hat \theta$를 찾는 것이다.

• n이 증가하면 $\hat\theta_{MAP} \to \hat\theta_{MLE}$
• MAP는 prior belief가 존재하고 정확하면 매우 강력한 estimator이다
• prior belief가 틀리다면 큰 오차가 발생할 수 있다.

prior는 마치 선입견과도 같아서, 좋은 prior를 가지면 더 빠르게 좋은 추론을 해낼 수 있고, 나쁜 prior를 가지면 나쁜 결과를 얻게 된다.

정리하자면 Bayes Theorem 결과(관측)에 대한 원인을 분석하는 방법으로, 사전 확률을 시작으로 데이터가 주어지면서 이 변화를 반영할 수 있다. 그렇기 때문에 좋은 가정이 있다면 더 좋은 유추를 할 수 있게 된다.