Variational Auto-Encoder

신희준·2022년 10월 18일

network

Background Knowledge

목록 보기

4/12

이활석 (NAVER) 님의 "오토인코더의 모든 것"을 보고 정리한 글 (모든 내용과 figure의 출처)

Reminder

Machine Learning Problem을 통계 추론의 근간이 되는 MLE의 관점에서 한번 다시 살펴보자. VAE를 이해하는데 필수이다.

소문자 $x,y$ 는 데이터 포인트 하나라고 생각해야 이해가 편하다

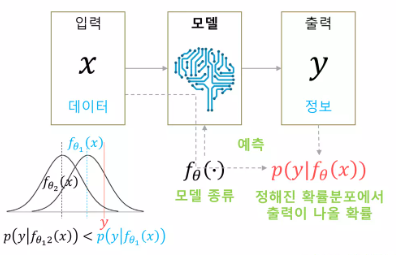
우리가 하고싶은 것은 network input $X$ 가 주어졌을 때, 정답 $Y$ 가 나올 conditional probability $P(Y|X)$ 를 추정하는 것.

Back Propagation 관점에서는 우리의 네트워크 출력 $f_\theta(x)$ 이 정답 $y$ 와 가까워 지기를 바라며, 두 값이 다른 정도를 loss로 정의하고 이를 최소화하는 방향으로 학습을 진행한다.

반면 MLE 관점에서는 $P(Y|X)$ 를 추정하기 위해 이를 $P(Y|\mathcal w=f_\theta(X))$ 로 파라미터화하여 parameter $\mathcal w$ 를 찾는 task로 변형시킨다. 네트워크 출력이 어떤 확률 분포의 parameter가 되고, 이 확률 분포 $p(f_\theta(x))$ 가 주어졌을 때, 정답 $y$ 가 나올 확률 $p(y|f_\theta(x))$ 을 최대로 하는 것을 목표로 한다고 해석할 수 있다. 확률 분포에 대한 likelihood가 maximize되고 싶으므로, 이 확률 분포 모델을 사전에 정하고 문제를 푼다.

** likelihood라는 것은 어떠한 데이터가 특정 분포로부터 생성되었을 확률로 생각할 수 있다.
$L(\theta)=P(X|\theta) \; \to \theta$ 라는 파라미터를 갖는 분포에서 $X$ 가 나올 확률

예를 들어 우리가 이 확률 분포 $p(f_\theta(x))$ 를 정규 분포로 가정했다고 하자. 그러면 우리는 네트워크를 통해서 확률 분포의 paramter, 즉, 평균을 추정하고자 하는 것이다. (편의를 위해 표준편차를 제외)

그러면 주어진 확률 분포에서, $y$ 는 fixed point이기 때문에 likelihood값을 구할 수 있는데, 위 그림을 보면 $f_{\theta_2}(x)$ 를 평균으로 갖는 정규 분포에서 $y$ 의 likelihood값이 매우 작은 것을 확인할 수 있다. 또한, 학습을 통해 parameter가 $\theta_1$ 이 되어 평균이 $f_{\theta_1}(x)$ 이 되는 정규분포에서는 $y$ 의 likelihood값이 더 큰 것을 알 수 있다.

정리하자면, $y$ 의 likelihood가 가장 높을 때는 네트워크 output, 즉, 정규 분포의 평균이 $y$ 가 될 때라는 것을 알 수 있고, 이 말은 앞서 정답 $y$ 가 network output $f_\theta(x)$ 와 가까워 지기를 바라는 관점과 동일하다.

loss는 likelihood $p(y|f_\theta(x))$ 를 최대화하기 위해 negative log likelihood $-log\;p(y|f_\theta(x))$ 를 최소화하는 것으로 정할 수 있다.

\theta^*= \underset{\theta}{argmin}[-log(p(y|f_\theta(x)))]

이 관점이 이 전의 관점과 가장 큰 다른점은 구하고자 하는 것이 내가 미리 가정한 확률 분포의 parameter가 된다는 점이다. 분포를 추정하게 될 경우, 고정된 입력에 따라 고정된 출력을 얻는 것이 아니라, 이 분포를 토대로 sampling을 할 수 있게된다.

y_{new}=p(y|f_{\theta^*}(x_{new}))

$\to$ 이것은 VAE가 다양한 출력을 낼 수 있게 하는 기본적인 원리이다.

MLE 관점으로 볼 때, 위의 negative log likehood는 어떤 의미를 가질까?

Gaussian distribution $f_\theta(x_i) = \mu_i \;, \sigma_i=1$

p(y_i|\mu_i,\sigma_i)=\frac{1}{\sqrt{2\pi}\sigma_i}exp(-\frac{(y_i-\mu_i)^2}{2\sigma_i^2})

log(p(y_i|\mu_i,\sigma_i))=log\;\frac{1}{\sqrt{2\pi}\sigma_i}-\frac{(y_i-\mu_i)^2}{2\sigma_i^2}

-log(p(y_i|\mu_i))=-log\frac{1}{\sqrt{2\pi}}+\frac{(y_i-\mu_i)^2}{2}

-log(p(y_i|\mu_i)) \propto \frac{(y_i-\mu_i)^2}{2} = \frac{(y_i-f_\theta(x_i))^2}{2}

$\to$ mean squared error와 같다.

Bernoulli distribution $f_\theta(x_i)=p_i$

p(y_i|p_i)=p_i^{y_i}(1-p_i)^{1-y_i}

log(p(y_i|p_i))=y_ilogp_i+(1-y_i)log(1-p_i)

-log(p(y_i|p_i))=-[y_ilogp_i+(1-y_i)log(1-p_i)]

$\to$ cross-entropy error와 같다.

즉, MLE 관점에서 likelihood를 최대화 한다는 것은, 확률 분포가 정규 분포일 때는 MSE를 최소화하는 것과 동일하고, 베르누이 분포일 때는 Cross-entropy error를 최소화하는 것과 동일하다.

그러므로 철학적으로는 conditional distribution $p(y|f_\theta(x))$ 가 gaussian distribution을 따르면 (예를 들면 output이 continuous) MSE를 쓰는 것이 낫고, bernoulli distribution을 따르면 (예를 들면 output이 not continuous; classification) cross-entropy loss를 쓰는 것이 낫다.

Variation Auto-Encoder

VAE는 실제로 코드를 보면 AE와 다른 점을 찾기가 어렵다. 하지만 실제로는 오히려 AE와 거의 관계가 없다.

Generative Model

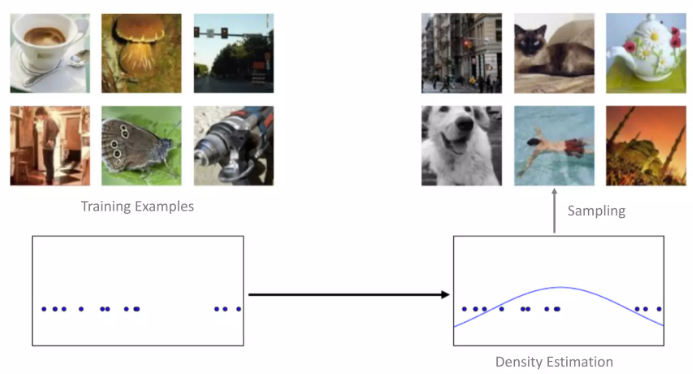
training database에 있는 데이터를 각 숫자 하나로 mapping한다고 생각해보자. generative model에서는 training database에 있는 point $x$ 를 이용해, 해당 database를 잘 표현하는 확률 분포를 찾아내는 것이고, 이 확률 분포를 잘 학습했다면, 이를 이용하여 새로운 data sample을 생성해낼 수 있을 것이다.

generative model에서는 어떤 사전 분포로부터 추출된 latent vector z가 주어졌을 때, training database의 $x$ 가 나올 likelihood를 최대화하고자 한다.

MLE에서와 마찬가지로 network(deterministic function)는 어떠한 확률 분포의 parameter( $g_\theta(z)$ )를 추정한다. 그러면 어떤 확률 분포를 가지고 training data x의 확률 분포 $p(x)$ 를 추정할 수 있는 것이다. (여기서 $x$ 는 training data 하나이다)

\int p(x|g_\theta(z))p(z)dz=p(x)

데이터를 generate할 때, 우리는 manifold에 있는 latent vector z를 이용하는데, 이 vector를 control하여 다양한 image를 만들어낼 것이므로, sampling하기 용이하고 제어하기 쉬운 normal distribtion이나, uniform distribution을 많이 사용한다.

그러면 prior도 정해놓았고, conditional probability $p(x|g_\theta(z))$ 도 정해놓았으므로 데이터 샘플을 쭉 뽑아서 summation하여 근사할 수는 없을까?

\sum_i p(x|g_\theta(z_i))p(z_i) \approx p(x)

$\to$ 결론적으로는 안된다. (VAE를 사용해야하는 이유)

위의 예시를 보자. (a)는 실제 database의 sample $x$ 이고, (b)는 왼쪽에 픽셀이 조금 지워진 example, (c)는 한 픽셀 오른쪽으로 옮겨진 example이다. 그러므로 (b)는 의미론적으로 (a)와 멀고, (c)는 사실 똑같은 이미지라고 생각할 수 있다.

하지만 실제로 MSE를 구해보면, (a)와 (c)사이의 MSE가 (a)와 (b)사이의 MSE보다 훨씬 크다. 아까 위에서 MLE의 관점에서 생각하면, 우리가 conditional probability(모델의 확률 분포)를 gaussian으로 가정한다면, gaussian의 평균이 (b)일 때, (a)의 likelihood가 더 높게 된다. 그 말은 바로 MLE를 적용하여 학습할 경우, 의미론적으로 더 먼 이미지가 생성될 확률이 크다는 것이다.

결론적으로 우리는 sampling 함수 $p(z_i)$ 를 잘 조절해야한다고 할 수 있다.

Variational Inference

prior distribution에서 sampling하니까 잘 학습이 되지 않았다. $\to$ 어떤 이상적인 sampling 함수에서 sampling하면 학습이 더 잘 되지 않을까?

그러므로 $x$ 를 보여주고, 적어도 이 $x$ 에 대해서는 잘 sampling하는 함수를 만들어보자. 하지만 우리는 이 함수를 알 수가 없으므로, 이 확률 분포를 추정하고자 할 때, variational inference를 사용한다.

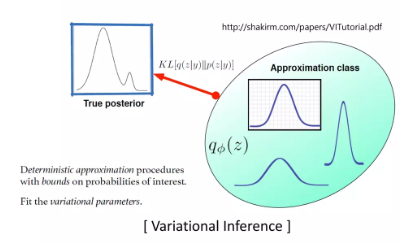
variational inference는 true posterior $p(z|x)$ 를 추정하기 위해서 우리가 알고 있는 확률 분포 (예를 들어 정규 분포)를 하나 선택해서 $q_\phi(z|x)$ , 그것의 파라미터를 조정하여 최대한 true posterior와 가깝게 만들어 보자는 것. 그 다음에 이 approximation class에서 $z$ 를 sampling하면 $x$ 가 잘 나올 것이다.

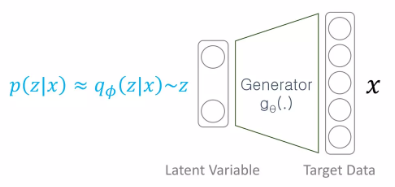
결국에 우리는 $p(x)$ 를 구하고 싶은 것인데, 이를 위해서 몇 가지 분포들이 도입되었으므로, 이들 사이의 관계를 한번 살펴보자.

Relationship along $p(x), p(z|x), q_\phi(z|x)$

log(p(x)) = \int logp(x)\;q_\phi(z|x)dz \;\because \int q_\phi(z|x)dz = 1

= \int log\frac{p(x,z)}{p(z|x)}\;q_\phi(z|x)dz \;\because p(x) = \frac{p(x,z)}{p(z|x)}

= \int log\frac{p(x,z)}{q_\phi(z|x)}\frac{q_\phi(z|x)}{p(z|x)}\;q_\phi(z|x)dz

= \underset{① ELBO(\phi)}{\underline{\int log\frac{p(x,z)}{q_\phi(z|x)}\;q_\phi(z|x)dz}} + \underset{② KL(q_\phi(z|x)||p(z|x))}{\underline{\int log\frac{q_\phi(z|x)}{p(z|x)}\;q_\phi(z|x)dz}}

정리하면 두 항이 나오는데, KL divergence는 두 확률 분포 간의 거리를 측정하는 함수로 항상 양수의 값이 나온다. KL에서 $p(z|x)$ 는 이상적인 sampling 함수였고, $q_\phi(z|x)$ 는 이를 추정하고자 하는 확률 분포이므로, variational inference입장에서는 이 두 분포를 최소화하는 목표를 이루기 위해서 해당 term을 최소화 해야한다. 하지만 우리는 $p(z|x)$ 를 모르기 때문에, 정해진 상수 $logp(x)$ 안에서 ELBO가 최대가 되는 파라미터 $\phi$ 를 찾아 이상적인 sampling 함수를 찾을 수 있다.

log(p(x)) =ELBO(\phi) + KL(q_\phi(z|x)||p(z|x))

q_{\phi^*}(z|x)= \underset{\phi}{argmax}\;ELBO(\phi)

ELBO(\phi)=\int log\frac{p(x,z)}{q_\phi(z|x)}\;q_\phi(z|x)dz

=\int log\frac{p(x,z)p(z)}{q_\phi(z|x)}\;q_\phi(z|x)dz

=\int log(p(x,z))q_\phi(z|x)dz - \int log\frac{q_\phi(z|x)}{p(z)}q_\phi(z|x)dz

=\mathbb{E}_{q_\phi(z|x)}[log(p(x|z))]-KL(q_\phi(z|x)||p(z))

이제, 우리는 최종적으로 두 가지 문제에 대해 optimization을 해야 한다.

Optimization Problem on $\phi$ : Variational Inference

logp(x) \geq \mathbb{E}_{q_\phi(z|x)}[log(p(x|z))]-KL(q_\phi(z|x)||p(z)) = ELBO(\phi)

Optimization Problem on $\theta$ : Maximum likelihood
$-\sum_ilog(p(x_i)) \leq \sum_i \mathbb{E}_{q_\phi(z|x)}[log(p(x_i|g_\theta(z)))]-KL(q_\phi(z|x_i)||p(z))$
Final Optimization Problem
$\underset{\phi, \theta}{argmin} \sum_i -\mathbb{E}_{q_\phi(z|x)}[log(p(x_i|g_\theta(z)))]+KL(q_\phi(z|x_i)||p(z))$

첫번째 Optimization은 이상적인 sampling 함수를 찾기 위해 ELBO를 maximize하는 것이였고, 두번째 Optimization은 generator에서 likelihood를 maximize하기 위해 negative log likelihood를 minimize하는 것이였다.

그런데 ELBO 식을 잘 보면, ELBO의 첫번째 항에서 이를 maximize하면 likelihood도 maximize하는 효과도 가진다는 것을 알 수 있다. 그러므로, ELBO를 maximize하면 최종 optimization문제를 푸는 것과 같다고 할 수 있다. $\phi$ 에 대해서 하면 encoder를 optimize, $\theta$ 에 대해서 하면 decoder를 optimize한다고 볼 수 있다.

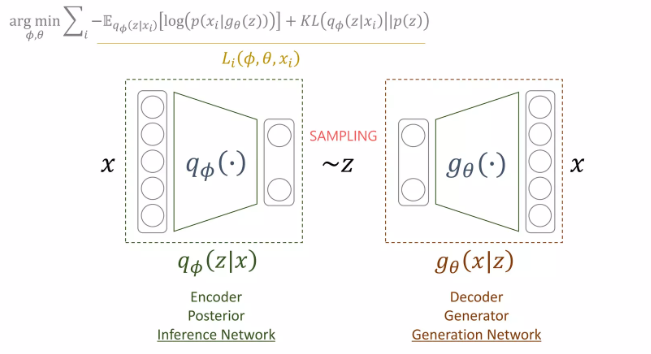
정리하자면, generator를 학습하고자 하는데, prior에서 sampling할 때 학습이 잘 안되므로, 이상적인 sampling 함수에서 sampling하고자 $x$ 를 evidence를 주고, $x$ 에 대해서는 잘 generate할 수 있는 $z$ 를 sampling할 수 있는 함수를 도입하였고, 이를 추정하기 위해서 $q_\phi$ 를 사용하였다.

이 $q_\phi$ 를 찾기 위해서는 ELBO term을 $\phi$ 에 대해서 maximize하는 것이고, 이 $q_\phi$ 를 통해 $z$ 를 sampling하여 generate한 $x$ 의 likelihood를 maximize하고자 하는데, 이 ELBO term을 maximize하는 것이 generator에서 $x$ 의 likelihood를 maximize하므로 $\theta$ 에 대해서 ELBO를 maximize하여 $g_\theta$ 를 최적화 한다.

이 과정에서 input이 $x$ 로 들어가고 output이 $x$ 로 들어가는 AutoEncoder와 같은 구조가 만들어진다. 이때 variation inference를 사용하므로 우리는 이것을 Variational Auto Encoder라고 부른다.

Loss Function

그러면 VAE의 loss function이 되는 ELBO를 조금 더 자세히 해석해보자.

L_i(\phi,\theta,x_i)= - \underset{Reconstrunction \;Error}{\underline{\mathbb{E}_{q_\phi(z|x_i)}[log(p(x_i|g_\theta(z)))]}} +\underset{Regularization}{\underline{KL(q_\phi(z|x_i)||p(z))}}

(1) Regularization

같은 reconstruction error를 갖는 상황이라면 이왕이면 prior와 같은 분포를 갖도록
sampling의 편의성, 생성 데이터의 통제성을 위한 조건을 prior에 부여했기 때문

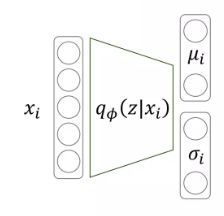
assumption 1. approximation class는 gaussian distribution

q_\phi(z|x_i)\sim N(\mu_i,\sigma_i^2I)

assumption 2. prior는 normal distribution

p(z)\sim N(0,I)

이상적인 함수를 찾기 위한 $q_\phi$ 를 gaussian으로 정했으므로, encoder를 통해서 찾을 파라티머는 $\mu_i$ 와 $\sigma_i$ 이다.

그리고 이때, 정규분포끼리의 KL divergence는 수식적으로 계산하기 쉽다.

KL(q_\phi(z|x_i)||p(z)) = \frac{1}{2}\sum_{j=1}^{J}(\mu_{i,j}^2+\sigma_{i,j}^2-ln(\sigma_{i,j}^2)-1)

(2) Reconstruction Error

maximum likelihood 관점에서 maximize하는 term
$x$ 가 주어졌을 때, 이상적인 함수를 approximate한 함수에서 $z$ 를 sampling하고 그 $z$ 를 generator에 넣었을 때, conditional probability를 maximize $\to$ 결국 $x$ 를 넣었을 때, $x$ 가 나오도록 하는 것

$q_\phi$ 가 정해진 상황에서는 gaussian으로 가정했기 때문에, 평균과 표준편차가 정해지고, 이 분포에서 $z$ 를 sampling하고, 이를 이용해 decoder를 학습 $\to$ decoder에 필요한 확률 분포 $\theta$ 를 찾아 likelihood의 mean을 구함

\mathbb{E}_{q_\phi(z|x)}[log(p(x_i|g_\theta(z)))] = \int log(p_\theta(x_i|z))q_\phi(z|x_i)dz

다 적분을 할 수 없으니, monte-carlo technique을 이용하여 구할 수 있다.

\frac{1}{L} \sum_{z^{i,j}} log(p_\theta(x_i|z^{i,j}))

근데 여기서 문제가 sampling이 들어가다보니(random node), back-propagation에서 문제가 생긴다.

Reparameterization trick

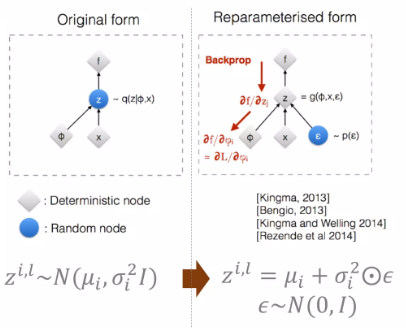
$z$ 를 우리가 구한 분포에서 바로 sampling하는 것이 아니라, normal distribution에서 $\epsilon$ 을 sampling하고 분산에 element-wise 곱하고, 평균을 더한 값을 사용한다.

이렇게 되면, $z$ 의 확률적 특성은 같으나, back propagation algorithm은 사용할 수 있게 된다. (결국 coding할 때의 trick임; 근데 사실 api에 내장 되어 있을거임)

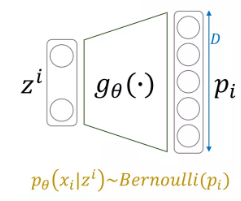
다시 돌아와서, monte-carlo technique을 쓴다고 했는데, 실제 training할 때는 그냥 sampling 갯수도 1로 사용한다. 즉, example 하나에 대해 log-likelihood값만 구하면 된다.

\frac{1}{L} \sum_{z^{i,j}} log(p_\theta(x_i|z^{i,j})) \approx log(p_\theta(x_i|z^{i}))

위에서 한번 다루었듯이, log-likelihood를 구할 때, conditional probability는 미리 정하고 간다. 그리고 보통 이미지에서는 bernoulli 분포를 가정한다.

log(p_\theta(x_i|z^{i})) = log \prod_{j=1}^Dp_\theta(x_{i,j}|z^i)=\sum_{j=1}^Dlogp_\theta(x_{i,j}|z^i)

=\sum_{j=1}^Dlogp_{i,j}^{x_{i,j}}(1-p_{i,j})^{1-x_{i,j}} \;\gets p_{i,j} \doteq network \; output

=\sum_{j=1}^Dx_{i,j}logp_{i,j}+(1-x_{i,j})log(1-p_{i,j}) \;\gets Cross \;Entropy

결국 log-likelihood를 구하면, network output $p_{i}$ 와 입력값 $x_i$ 사이의 cross-entropy error가 된다.

반면에 gaussian으로 가정하면, 위에서 살펴보았듯이 Squared-error가 된다는 것을 알 수 있다.

Architecture

지금까지 살펴본 VAE의 구조를 종합하면 다음과 같은 structure가 만들어질 수 있다.

Gaussian Encoder + Bernoulli encoder
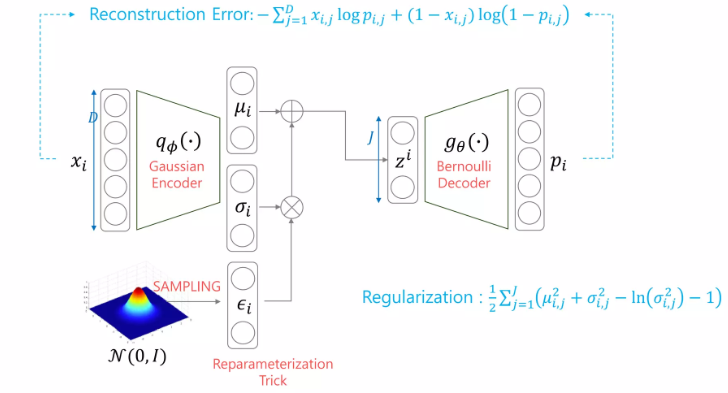
Gaussian Encoder + Gaussian Decoder
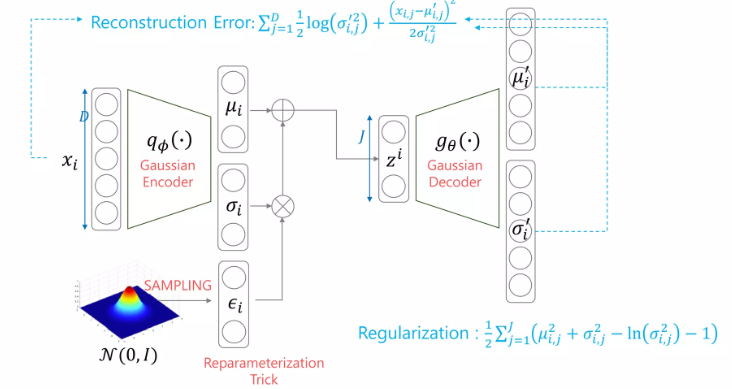
Gaussian Encoder + Gaussian Decoder with Identity Covariance

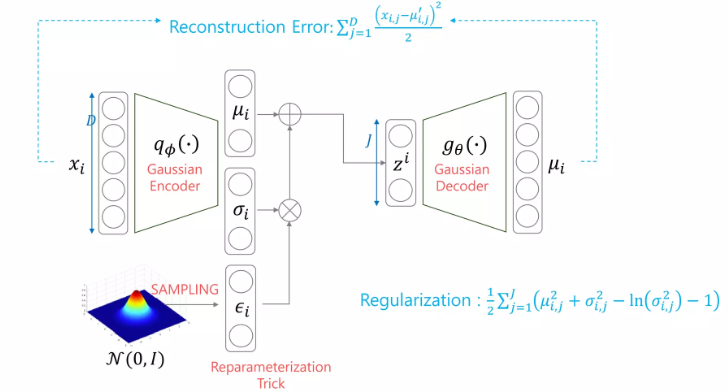
Discussion

(1) Variation Auto Encoder와 Auto Encoder는 실제로 수학적으로는 많이 다르지만, 코드 입장에서 다른 점은 regularization term이 추가되었다는 것 말고는 다른 점이 없는데 (물론 정규분포에서 sampling이 추가 되기는 함) 저 regularization term이 어떠한 역할을 할까?

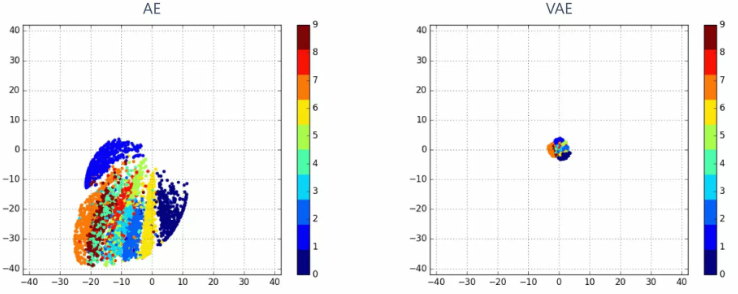
위의 TSNE는 학습이 끝난 AE와 VAE에서 테스트 샘플 5000개의 manifold $z$ 가 어느 위치에 mapping되는지 보여주는 plot이다. (MNIST 결과로 색의 label을 의미)

다시 한번 이야기하자면, AE는 데이터 압축이 목적이였고, VAE는 데이터 생성이 목적이였다.

둘 다 reconstruction 성능이 비슷한 상황에서, AE가 생성한 manifold를 보면 의미있는 이미지가 생성되는 manifold space의 위치가 매번 바뀐다. (그림에는 표현이 안되지만, 학습할 때마다 어디에 찍히는지 알 수 없다) 반면에 VAE는 KL divergence를 regularization으로 주어 prior distribution과 distribution이 비슷해졌다.

이미지를 잘 압축하여 manifold space에서 구분하는 것에는 전혀 문제가 없지만, 생성관점에서 이 둘은 완전히 다르다. 생성 관점에서는 다루고자 하는 manifold의 위치가 안정적인 것이 중요하다.

즉, 이미지를 생성해보려고 할 때, AE의 경우 $z$ 값을 어떻게 어디서 sampling할 지 알 수 없지만, VAE의 경우, 쉽게 prior distribution에서 sampling하면 의미있는 이미지를 얻을 수 있다.

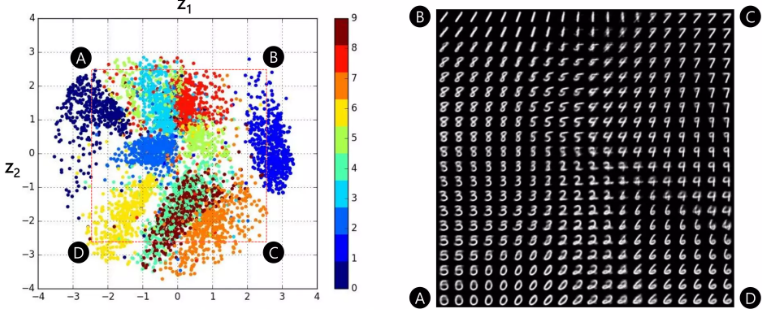
VAE를 통해 생성된 manifold space를 더 자세히 보면 위와 같다. 전체적으로 $z$ 값이 normal distribution, 즉 prior를 따르고 있고, 의미 있는 이미지들끼리 뭉쳐 있는 것을 알 수 있다. 각 cluster에서 $z$ 를 sampling하여 이미지를 생성해보면 이미지가 유의미하게 잘 생성되는 것을 확인할 수 있다.

(2) Encoder에서는 왜 Gaussian distribution만 쓸까? 다른 분포에 대해 KL을 구하기가 너무 어려움 --> Adversarial AutoEncoder

Adversarial AutoEncoder

Introduction

VAE의 variation을 보면 모두 decoder의 확률 분포를 다르게 가정하는 경우뿐이였다. encoder를 바꾸지 못하는 이유는 결국 KL term 때문인데, gaussian 분포가 아닌 경우 계산하기가 너무 어렵기 때문이였다.

L_i(\phi,\theta,x_i)= - \mathbb{E}_{q_\phi(z|x_i)}[log(p(x_i|z))] +\underset{Regularization}{\underline{KL(q_\phi(z|x_i)||p(z))}}

$q_\phi(z|x_i)$ 와 $p(z)$ 의 조건
(1) 분포로부터 sample을 뽑기가 쉬워야 한다.
(2) KL이 계산될 수 있어야 한다.

이러한 제약을 없애기 위해 사용할 수 있는 방법이 Adversarial Autoencoder이다. 즉, KL을 계산하지 않고, 두 분포 $q_\phi(z|x_i)$ 와 $p(z)$ 가 같도록 만들어 보자.

Generative Adversarial Network

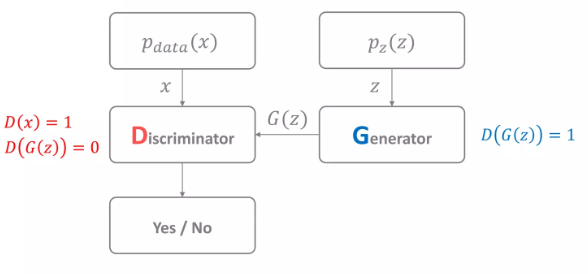
위의 그림은 매우 간단한 GAN의 구조이다. GAN은 maximum likelihood를 사용하는 기법 중에서 확률 분포 모델을 정하지 않고 학습하는 기법이다.

prior $p_z(z)$ 에서 sampling하여 generator가 fake sample을 만들어낸다. 또한, true distribution $p_{data}(x)$ 에서 데이터를 real sample을 sampling한다. $p_{data}(x)$ 는 실제 우리가 추정하고자 하는 training database를 설명하는 분포이지만, 실제로는 그냥 training data를 넣어준다고 생각할 수 있다.

discriminator는 단순히 real sample과 fake sample을 구분하는 것이라고 볼 수 있다. real sample을 1, fake sample을 0이라고 한다면, discriminator는 sample을 구분하도록 학습되고, generator는 fake sample을 discriminator가 1로 판단하도록 학습된다. (함께 학습)

GAN에서 최종 목표는 $G(z)\sim p_{data}(x)$ 로 만드는 것이다.

V(D,G) = \mathbb{E}_{x\sim p_{data}(x)}[logD(x)]+\mathbb{E}_{z\sim p_{z}(z)}[log(1-D(G(z)))]

즉, 위의 value function을 discriminator 입장에서는 maximize해야하고 generator 입장에서는 minimize해야한다.

D^*,G^*=\underset{G}{min}\underset{D}{max}V(D,G)

하지만 위의 수식에서 볼 수 있듯이, 두 네트워크에 대해 같은 function을 하나는 maximize, 하나는 minimize하므로 균형을 맞춰 학습시키기가 매우 어렵다.

Architecture

GAN의 개념을 도입하여 VAE에 적용하면 다음과 같은 구조를 갖게 된다.

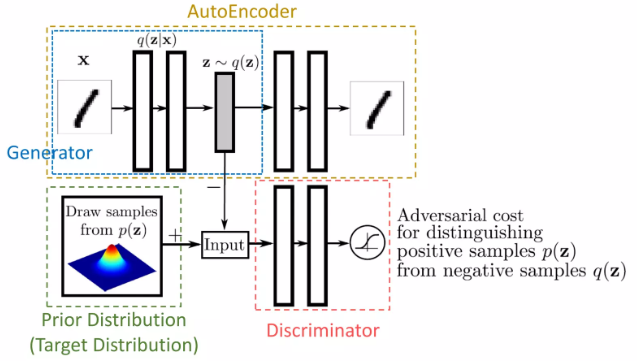
VAE에서 KL term은 $q_\phi$ 와 prior를 갖게 만드는 역할을 수행했다. 여기서도 같은 목적을 달성하기 위해, prior에서 추출하는 $z$ 를 +(real)로 하고, generator(VAE에서는 encoder가 $z$ 를 만듦)가 만드는 $z$ 를 -(fake)로 하여 discriminator를 두고 이를 구분하도록 한다.

그러면 KL term을 쓰지 않고도 두 분포를 같게 만들어줄 수 있다. 이때, $q_\phi$ 의 분포를 미리 정하지 않음도 알 수 있다.

Loss Function

원래의 KL term을 삭제하고 GAN Loss를 사용한다.

L_i(\phi,\theta,x_i)= - \mathbb{E}_{q_\phi(z|x_i)}[log(p(x_i|z))] +\cancel {KL(q_\phi(z|x_i)||p(z))}

V(D,G) = \mathbb{E}_{x\sim p_{data}(x)}[logD(x)]+\mathbb{E}_{z\sim p_{z}(z)}[log(1-D(G(z)))]

VAE는 하나의 structure가 같은 목적을 가지고 학습하기 때문에 한번에 학습해도 되지만, GAN은 네트워크가 서로 다른 목적을 가지기 때문에 step by step으로 학습한다.

AutoEncoder : $\phi$ 와 $\theta$ 를 recon error에 대해 학습
$L_i(\phi,\theta,x_i)= - \mathbb{E}_{q_\phi(z|x_i)}[log(p_\theta(x_i|z))]$
Discriminator : $\lambda$ 를 학습
$-V_i(\phi,\lambda,x_i,z_i)=-logd_\lambda(z_i)-log(1-d_\lambda(q_\phi(x_i)))$
Generator : $\phi$ 를 학습
$-V_i(\phi,\lambda,x_i,z_i)=-log(d_\lambda(q_\phi(x_i)))$

discussion

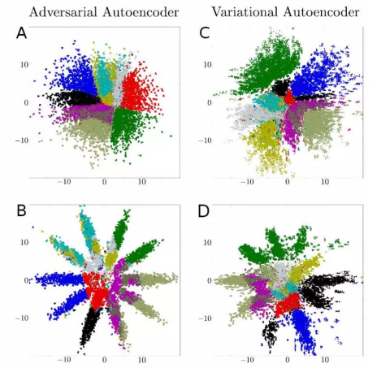
위의 그림은 AAE와 VAE의 manifold space를 가시화 한 것이다. A, C는 normal distribution의 prior를 사용하고, B, D는 10개의 gaussian의 mixture를 prior로 하고 학습한 경우이다.

A, C를 보면 둘 다 normal discribution을 따르도록 나름 잘 학습이 되었지만, B, D를 보면 AAE는 이 prior의 분포와 같게 형성이 잘 되지만, VAE는 normal distribution을 가정할 수 밖에 없기 때문에 분포의 모양이 prior를 따르지 못한다.