Paper : FAST-LIO: A Fast, Robust LiDAR-inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter (Wei Xu, Fu Zhang / IEEE RAL 2021)

code: https://github.com/hku-mars/FAST_LIO

Highlights

• Tightly-Coupled iterated Kalman Filter를 사용하여 Lidar-IMU 센서 데이터 fusion
• Kalman gain을 효율적으로 계산하는 방법을 제시하여 cost를 줄임
• Backward propagation을 사용하여 motion distortion 보정

Introduction

• Visual SLAM의 단점 : 직접적인 깊이 추정이 불가하며, 3D 환경을 recon하는데 더 큰 리소스가 필요함. 특히, lighting condition에 취약
• LiDAR 센서는 이러한 어려움을 극복하지만, 작은 크기의 로봇을 위해 사용되기에는 too costly and bulky
• Solid-state LiDAR는 상대적으로 저렴하고, 성능이 좋아서 UAV에 많이 사용되고 있지만 몇 가지 문제점이 있음
  • LiDAR feature는 주로 geometrical structure (edges & planes)이기 때문에 feature가 부족한 환경에서는 LiDAR SLAM의 성능이 저하
  • LiDAR scan은 많은 feature point를 생성하는데, 이는 모두 정확하지는 않기 때문에, 정확한 pose 추정을 위해 IMU와 tightly fuse가 필요함. 하지만 UAV onboard computer가 이를 수행하기에는 computation cost가 너무 큼
  • LiDAR가 laser/receiver pair를 통해 순차적으로 point를 sampling하기 때문에, scan의 laser point은 서로 다른 시간에 sampling되며 이는 motion distortion을 일으켜 scan registration 성능을 저하
  • UAV propeller와 motor의 움직임으로 인해 IMU에 많은 노이즈가 존재

Related works

• Loosely-coupled LiDAR-Inertial Odometry vs. Tightly-coupled LiDAR-Inertial Odometry
  • LiDAR Odometry and Mapping : Lidar를 통해서 starting point로부터 현재의 relative pose를 추정 (LOAM)
  • Loosely-coupled LiDAR-Inertial Odometry : LiDAR measurement와 IMU measurement를 각각 처리해서 그 결과를 나중에 fuse하는 방법 → new scan의 pose와 system의 여러 다른 state (velocity 등) 사이의 correlation을 무시한다는 단점
    
  • Tightly-coupled LiDAR-Inertial Odometry : LiDAR의 scan registration result 대신에 raw feature point와 IMU를 fuse하는 방법
    • optimization-based 와 filter-based로 다시 나눌 수 있음

→ FAST-LIO는 tight-coupled LiDAR-Inertial Odometry이며, filter-based method.

Methodology

Framework Overview

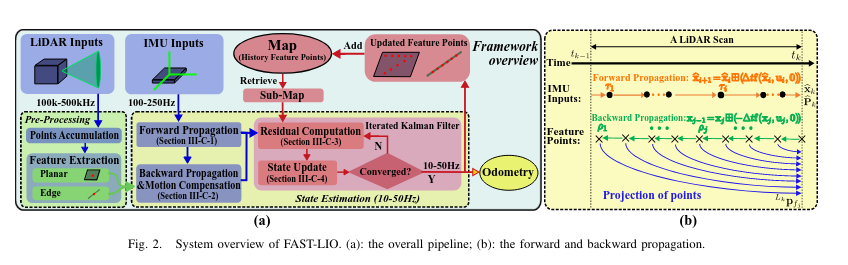
1) LiDAR input를 feature extraction module로 넣어 planar & edge feature를 얻는다.

2) 추출된 feature와 IMU measurement가 state estimation module로 들어간다.

3) Estimated pose는 feature point를 global frame으로 register하고 map과 merge

4) Update된 map은 다음 step에서 새 point를 register하는데 사용됌

• paper에서 사용되는 notation은 아래와 같음

System description

Encapsulation operator

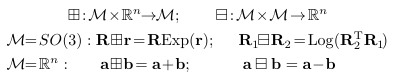
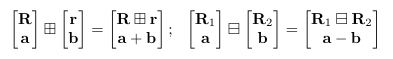
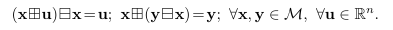
• 위 연산은 Lie Group의 plus / minus operator처럼 작동 (fig ref: https://alida.tistory.com/9)

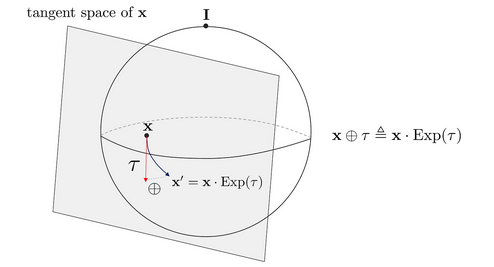
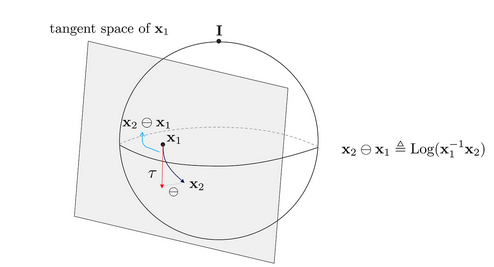
• Manifold가 단순 vector space일 때는 원래 처럼 계산

Continuous model

• IMU sensor가 LiDAR와 아래의 known extrinsic을 가지고 rigid하게 부착되어있다고 하자.

• IMU frame ($I$)를 reference body frame이라고 하면, 아래와 같은 운동방정식 유도 가능
  • $^Gp_I, ^GR_I$는 Global frame에서 IMU의 position과 attitude (Global frame $G$는 첫번째 IMU frame으로 정함)
  • $^Gg$는 global frame에서 중력 vector
  • $a_m,w_m$은 IMU measurement
  • $n_a,n_w$는 IMU의 white noise
  • $b_a,b_w$는 IMU의 random walk process bias ($n_{ba}, n_{bw}$의 gaussian noise를 갖는)
  • $\lfloor a \rfloor _{\mathrel{\wedge}}$ : skew-symmetric matrix (3d vector를 cross-product operation으로 mapping하기 위해 사용)

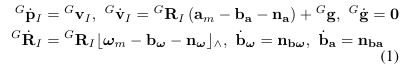
Discrete model

• 위에서 정의한 encapsulation operator를 기반으로 바로 위의 continuous model을 IMU sampling period $\Delta t$로 discretize

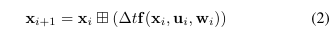
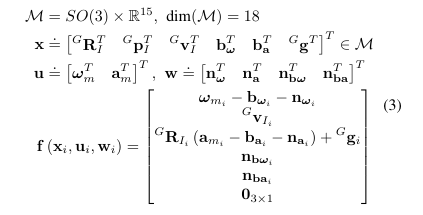
• $f$ 함수는 (1)의 식을 행렬 형태로 쓴 것일 뿐

Preprocessing of LiDAR measurement

• raw LiDAR point는 매우 빠르게 sampling되기 때문에 (~ 200kHz), 각 point가 받아질 때 바로바로 처리하는 것이 불가능
• FAST-LIO에서는 특정 시간동안 point를 누적하고 한번에 처리하는데, 최소 20ms동안 point를 누적시키며, 50Hz로 state estimation을 수행 (Odometry output)하며, map update.
• 이렇게 누적된 point set을 scan 이라고 하며, 이를 처리하는 시간을 $t_k$라 하자.
• LiDAR의 raw point로부터 local smoothness를 계산하고, 높은 smoothness를 갖는 point를 planar point / 낮은 smoothness를 갖는 point를 edge point로 추출한다.

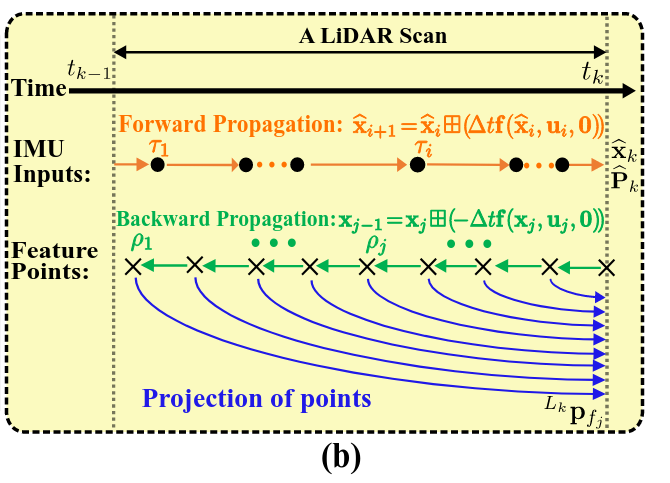
• 이때 하나의 scan에서 feature point의 갯수를 $m$개라고 하면, 각 point는 time $\rho_j \in (t_{k-1},t_k]$에서 sampling되었으며, 이를 $^{L_j}p_{f_j}$라고 하자. ($L_j$는 time $\rho_j$에서 LiDAR의 local frame)
• LiDAR scan 사이에서 IMU measurement도 매우 많이 존재하며, 각 IMU measurement는 time $\tau_i \in [t_{k-1}, t_k]$에서 $x_i$의 state를 가진다.
• 여기서, LiDAR의 마지막 feature point는 scan의 끝을 의미하며 ($\rho_m=t_k$), IMU measurement는 꼭 scan의 시작과 끝에 align될 필요가 없다.

State Estimation

• state estimation으로는 iterated extended Kalman filter를 사용
• time $t_{k-1}$의 LiDAR scan의 optimal state estimate을 $\bar{x} _{k-1}$이라하고 이때 공분산 행렬은 $\bar{P}_{k-1}$이라하자.
• 그러면 $\bar{P}_{k-1}$은 random error state vector의 공분산이 된다.
  • 여기서 $\delta \theta=Log(^G\bar{R}_I^{T}$ $^G R_I)$인 attitude error이며, 나머지는 모두 차이를 의미 ($\tilde{x}=x-\bar{x}$)
  • $x$는 실제 pose를 의미

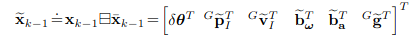
• Error definition의 가장 큰 장점은 attitude uncertainty를 3x3의 공분산 행렬 $\mathbb E\{\delta \theta \delta \theta^T\}$로 표현할 수 있다는 것.
  • Direct estimation을 수행하는 것에 비해서 error를 사용하면 실제 값과 추정 값의 아주 작은 deviation을 사용하게 되므로 linearization이 쉬워짐
  • Attitude 는 3DOF를 가지기 때문에 3x3 representation이 minimum representation

Forward Propagation

• Forward propagation은 IMU input이 받아질 때마다 수행된다.
• 아래와 같이 process noise를 0으로 설정하여 state vector를 update한다.

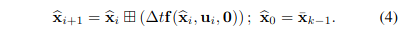
• Error state dynamic model은 아래와 같이 얻어진다. ($\Delta t=\tau_{i+1}-\tau_i)$

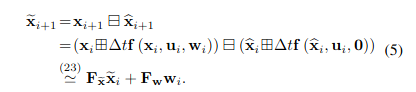
• 공분산은 error state dynamic model 식을 활용해서 구할 수 있다. (유도 과정 생략)

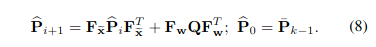
• Propagation은 scan의 끝인 $t_k$까지 진행되며, 이때 propagated state와 covariance는 $\hat{x}_k,\hat{P}_k$. 중요한 점은, $\hat{P}_k$는 ground truth state $x_k$와 state propagation $\hat{x}_k$ 사이의 error의 공분산이다.

Backward Propagation and Motion compensation

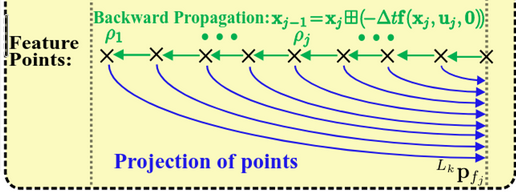
• LiDAR point의 누적이 $t_k$까지 도달했을 때, scan의 feature point를 propagated state와 covariance와 fuse하여 optimal state update를 수행할 수 있다.

• 하지만, 맨 처음에 언급했듯이, scan은 $t_k$에서 존재하는 반면, feature point는 각각 서로 다른 sampling time $\rho_j \le t_k$에 존재하기 때문에, reference body frame과의 mismatch가 생길 수 있다.

• 이러한 time $\rho_j$와 $t_k$의 상대적인 motion (motion distortion)을 보상하기 위해 아래의 식 (2)를 backward로 propagate시킨다.

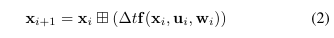
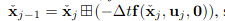
• Backward propagation은 feature point의 frequency로 실행되며, 이는 보통 IMU rate보다 훨씬 높다. 그러므로 두 IMU measurement 사이에서 sampling된 feature point들에 대해서는 left IMU measurement를 사용한다.

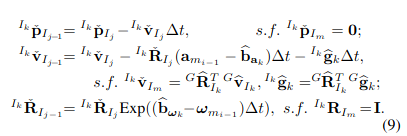
• 여기서 $\rho_{j-1} \in [\tau_{i-1},\tau_i), \Delta t = \rho_j-\rho_{j-1}$, $s.f.$는 starting from을 의미

• Backward projection을 통해 time $\rho_j$와 scan이 끝나는 시간인 $t_k: ^{I_k}T_{I_j}=(^{I_k}R_{I_j}, ^{I_k}p_{I_j})$ 사이의 상대적인 pose를 계산할 수 있고, 이 상대적인 pose는 local measurement $^{L_j}p_{f_j}$를 scan-end measurement $^{L_k}p_{f_j}$로 projection할 수 있게 해준다.

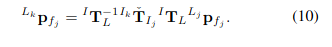
• $^I T_L$은 LiDAR-IMU extrinsic (known)
• 이 projection된 LiDAR point $^{L_k}p_{f_j}$들은 곧 바로 residual을 계산하는데 사용된다.

---

• 다시 쉽게 정리하자면, $t_k$에서 state를 기준으로 (pose, velocity, bias 등을 zero로 두고 시작) 역으로 feature point마다 state를 계산한다. 그러면 각 LiDAR point를 받았을 때의 pose를 알 수 있게 되고, 이 pose를 이용해 해당 LiDAR point들을 다시 $t_k$에서의 frame으로 projection시킬 수 있게 된다.

---

Residual Computation

• 예측한 state가 얼마나 정확한지 계산하기 위해 residual computation → LiDAR로 얻은 point cloud가 얼마나 기존의 map과 일치하는지 계산

• Backward projection을 통한 motion compensation을 통해, feature point의 scan을 모두 동시간 $t_k$에서 바라볼 수 있게 됌

• Iterated Kalman filter의 현재 iteration을 $\kappa$라고 하자. 그 때의 state estimation은 $\hat{x_k}^\kappa$

• Feature point $\{^{L_k}p_{f_j}\}$들은 아래 식으로 global frame으로 변환할 수 있다.

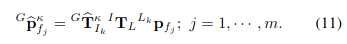
• 각 LiDAR feature point들에 대해, 현재 map에서 가장 가까운 feature point (plane or edge)가 실제 해당 point가 있어야 하는 곳으로 여겨진다. → 즉, residual $z^{\kappa}_j$은 feature point의 estimated global frame coordinate $^G \hat{p}^{\kappa}_{f_j}$와 그와 가장 가까운 plane 이나 edge $^G q_j$ 사이의 거리가 된다.

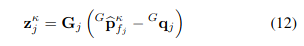
• 여기서 $G_j$는 normal vector (or edge orientation)를 의미 $G_j=u^T_j$ for plane $G_j=\lfloor u_j \rfloor _{\mathrel{\wedge}}$
• $u_j$의 계산이나 map에서 nearby point의 탐색은 KD-tree를 통해 이루어진다.
• 추가적으로, residual은 norm (distance)이 일정 수준 이하인 것만 고려하며 (0.5m) 이것보다 큰 residual들은 outlier이거나 새로 관측된 point이다.

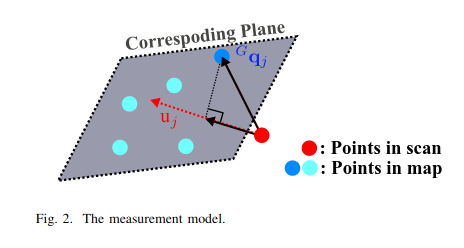
fig from FAST-LIO2 paper

• 계산된 residual $z^\kappa_j$와 state prediction $\hat{x}_k,$ covariance $\hat{P}_k$를 fuse하기 위해, $z^\kappa_j$와 ground-truth state $x_k$ 를 mapping시키는 measurement model을 linearize해야한다.
• LiDAR에서 얻어진 Point $^{L_j}p_{f_j}$의 noise $^{L_j}n_{f_j}$를 제거하면 true point 위치를 얻어낼 수 있다.

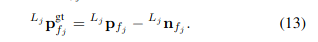
• 이 true point를 lidar scan이 끝난 시점의 frame인 $L_k$로 projection시킨 후, ground-truth state인 $x_k$와 함께 global frame로 변환시킨 점은 정확하게 map의 plane & edge와 일치해야한다.

• 즉, 위 (13)번 식을 아래와 같이 projection 시키고, global frame으로 변환시키고, residual을 구하면, 0이 되어야한다.

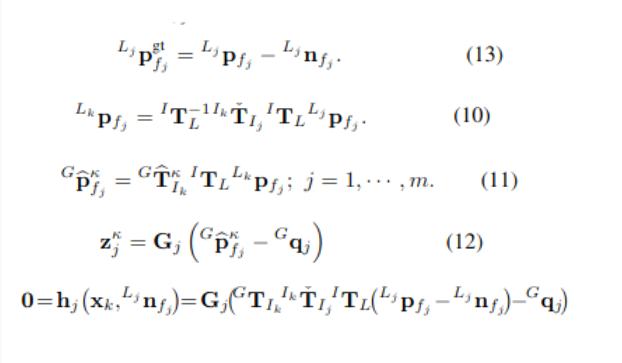
• 위 마지막 식인 관측 모델을 first order approximation하면 아래와 같이 정리된다.

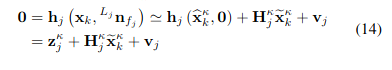
• $z^\kappa_j$는 noise가 0일 때 measurement model
• $H_j^\kappa$는 $h_j$의 $\tilde{x}^\kappa_k$에 대한 Jacobian matrix (error state에 대해 linearize)
• error state는 아래와 같음

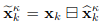
• $v_j \in \mathcal N(0,R_j)$는 raw measurement noise $^{L_j}n_{f_j}$로부터 구해짐

Iterated state update

• Forward propagation으로부터 predicted된 propagated state $\hat{x}_k$와 covariance $\hat{P}_k$는 unknown gt state $x_k$에 대해 gaussian prior를 부여
• 또한 $\hat{P}_k$는 error state의 covariance.
• 즉, $x_k \sim \mathcal N (\hat{x}_k,\hat{P}_k), x_k-\hat{x}_k \sim \mathcal N(0, \hat{P}_k)$

---

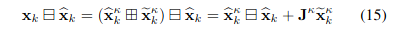
• 여기서 prior distribution of $x_k$는 time step $k$에서 마지막 measurement를 도입하기 전에 $x_k$에 대한 belief정도를 의미한다. 즉, forward propagation에서 구한 $x_k$의 분포
• posterior는 current measurement $z_k$를 합친 후의 state $x_k$에 대한 belief

---

• Jacobian $J^\kappa$는 위 식의 $\tilde{x}^\kappa_k$에 대한 편미분으로 구할 수 있다.

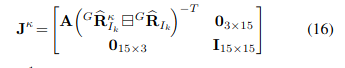
• 첫번째 iteration에서는 $\hat{x}^\kappa_k=\hat{x}_k$이고, $J^\kappa=I$

• 식 (15)의 prior와 식 (14)의 posterior를 합치면 maximum a-posteriori estimate (MAP) 식을 얻을 수 있다.

---

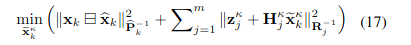
** Bayesian inference

→ 쉽게 이야기해서, prior knowledge (prior distribution)와 new data (likelihood)를 더하여 updated belief (posterior distribution)을 얻는 과정

• Bayes theorem

• Kalman Filter와 연동

  • Prior distribution → $P(x_k)$ : prediction step으로부터 얻은 state의 분포
  • Likelihood → $P(z_k|x_k)$ : 현재 state $x_k$에서 현재 measurement $z_k$가 얻어질 likelihood
  • Posterier distribution → $P(x_k|z_k)$ : 현재 measurement를 추가하였을 때, update된 state $x_k$의 분포

• MAP estimate : MAP estimate는 posterior distribution을 최대화하는 state를 찾는 것으로, EKF에서는 prior와 measurement 정보를 결합한 cost function을 최소화하는 것으로 구현

  • Posterior maximization (optimal state estimate $\bar{x}_k$)

    $\bar{x}_k = argmax_{x_k}p(x_k|z_k)$

  • Likelihood 와 Prior (prediction에서 얻어진) : bayes’ theorem으로 인해

    $\propto argmax_{x_k}p(z_k|x_k)p(x_k)$

  • Gaussian assumption : prior와 likelihood가 gaussian이면, 수학적 특성 활용 가능

    • 만약 measurement noise가 gaussian이라면, likelihood는 아래와 같이 쓸 수 있음 (gaussian의 pdf에 의해)

      $p(z_k|x_k)=\mathcal N(h_j(x_k),R_j)$
      $p(z_k|x_k)\propto exp(-\frac{1}{2}((z_k-h_k(x_k))^TR_j^{-1}(z_k-h_j(x_k)))$

    • 만약 state $x_k$ 에 대한 prior belief가 gaussian이면 아래와 같이 쓸 수 있음

      $p(x_k)=\mathcal N(\hat{x}_k,P_k)$
      $p(x_k) \propto exp(-\frac{1}{2}((x_k-\hat{x}_k)^TP_k^{-1}(x_k-\hat{x}_k))$

  • 이 수식들을 bayes’ theorem 식에 합치면

    $p(x_k,z_{1:k})\propto p(z_k|x_k)p(x_k)$
    $p(x_k|z_{1:k}) \propto exp(-\frac{1}{2}[(z_k-h_k(x_k))^TR_j^{-1}(z_k-h_j(x_k))+(x_k-\hat{x}_k)^TP_k^{-1}(x_k-\hat{x}_k)])$

  • Posterior를 maximize하기 위해서는, negative log를 minimize하면 된다.

    $argmin_{x_k}((z_k-h_k(x_k))^TR_j^{-1}(z_k-h_j(x_k))+(x_k-\hat{x}_k)^TP_k^{-1}(x_k-\hat{x}_k))$

  • 위 식을 정리해서 해당 논문의 MAP optimization 식 얻어낼 수 있음

---

• MAP 식에 (15)에서 linearize한 식을 대입하여 정리하고, 최적화 식을 풀면 아래와 같이 반복 update를 수행할 수 있다.

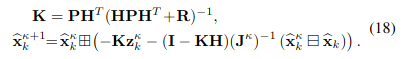
• 어느 수준으로 convergence가 된 후에는 optimal state estimation과 covariance는 다음과 같다.

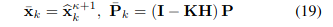
• 여기서 문제는, (18)식에서 볼 수 있듯이 kalman gain을 구할 시에 $HPH^T+R$의 역행렬을 구해야하는데, LiDAR feature point의 수가 너무 많아 역행렬을 구하는 것이 어렵다. 이를 해결하기 위해 kalman gain을 아래와 같이 구하는 방법을 제안하였다.
• 이렇게 하면, measurement의 dim이 아닌 state dim을 가지는 두개의 matrix에 대한 역행렬만 구하면 되어서 계산 부담이 덜하지만, 결과는 같다고 한다.

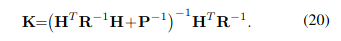
• 알고리즘 정리 --> 위의 내용들을 쭉 따라온 것

Map Update

• state update $\bar{x}_k$ 가 끝난 후 (즉, $^G\bar{T}_{I_k}= ( ^G\bar{R}_{I_k}, ^G\bar{p}_{I_k} )$), body frame $L_k$에서 정의된 각 feature point $^{L_k}p_{f_j}$는 global frame으로 옮겨진다.

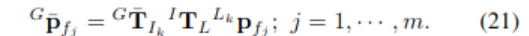
• 그리고 이 feature point들이 이전의 map이 추가됨으로써 map을 update한다.

Initialization

• System state의 good initial estimate를 얻기 위하여 FAST-LIO는 2초정도 LiDAR를 가만히 둔 상태에서 데이터를 수집하고, 이를 통해 IMU bias와 gravity vector를 초기화한다고 한다.

Result

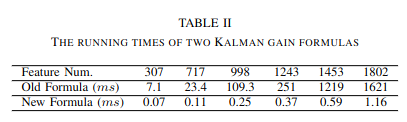
Computational Complexity Experiments

• Kalman gain 계산식 변경으로 인한 running time 개선

UAV Flight Experiments

• small-scale quadrotor로 비행 실험
  • Livox Avia LiDAR with 70 FoV
  • DJI Manifold 2-C onboard computer (Intel i7-8550U CPU)

• LI-odometry가 FC로 보내 trajectory tracking

• drift < 0.3%
• large rotation에 대해서도 잘 작동

Discussion

• KF, EKF, ESKF, IESKF 등 칼만 필터에 대한 배경지식이 많이 필요해서 이해하는데 시간이 좀 걸렸다.
• 그래도 전체적인 알고리즘 흐름이 단순해서, 순서대로 쭉 읽어보면 자세한 공식 유도과정을 제외하고는 이해할만 했다. prediction & update가 어떻게 일어나는지에만 집중해도 충분한 듯.
• 논문 자체가 methodology 위주라서 ablation result는 많지는 않아보인다.
• FAST-LIO의 가장 큰 장점은 processing speed이다. 다른 부분보다도 real-time processing에 집중해서 설계된 알고리즘이기 때문에 실제 UAV 에서도 실험을 하여 활용도가 높다고 생각한다.
• 그 와중에도 UAV에는 intel i7 cpu가 달린 DJI manifold를 사용하였기 때문에, 완전 lightweight한 모델인가에는 의문이 좀 든다. 찾아보니까 연구팀에서 올린 영상중에 ARM 4GB RAM cpu로도 real-time processing하는 영상이 있기는 하다.
• GIT에 코드가 사용하기 아주 편하게 정리되어 있어서 조만간 한번 mid-360을 이용해 적용해보려 한다. 개인적으로는 GPU processing 버전이 나왔으면 좋겠다.
• 다음에는 또 다른 훌륭한 LIO SLAM method인 LIO-SAM에 대해서도 공부해보려 한다. 해당 방법은 IMU-preintegration과 factor graph optimization을 활용한다.