Information, Entropy, & Cross-Entropy 이해

신희준·2024년 2월 22일

Background Knowledge

목록 보기

12/12

References:

https://www.youtube.com/watch?v=ErfnhcEV1O8

https://pytorch.org/docs/stable/index.html
이번 포스팅에서는 Deep learning에서 자주 사용되는 Cross-Entropy Loss의 개념과 그 기원에 대해서 알아보자.

Information Theory

Cross-Entropy의 개념은 Claude Shannon의 A mathematical theory of communication에서 제안된 Information theory에서 기원하였다.

Information theory은 간단하게 말해서 발신자가 수신자에게 효율적으로 message를 전달하는 방법에 관한 것이다.

기본적으로 digital signal을 통한 message 전달은 bit를 통해 이루어지는데, bit는 0 또는 1로 이루어진 수이다.

bit=0\;or\;1

Information theory에 따르면 1 bit의 information을 전송한다는 것은 수신자의 uncertainty를 절반으로 줄여준다는 것을 의미한다.

기상청에서 우리에게 날씨 정보를 전달해주는 상황을 생각해보자.

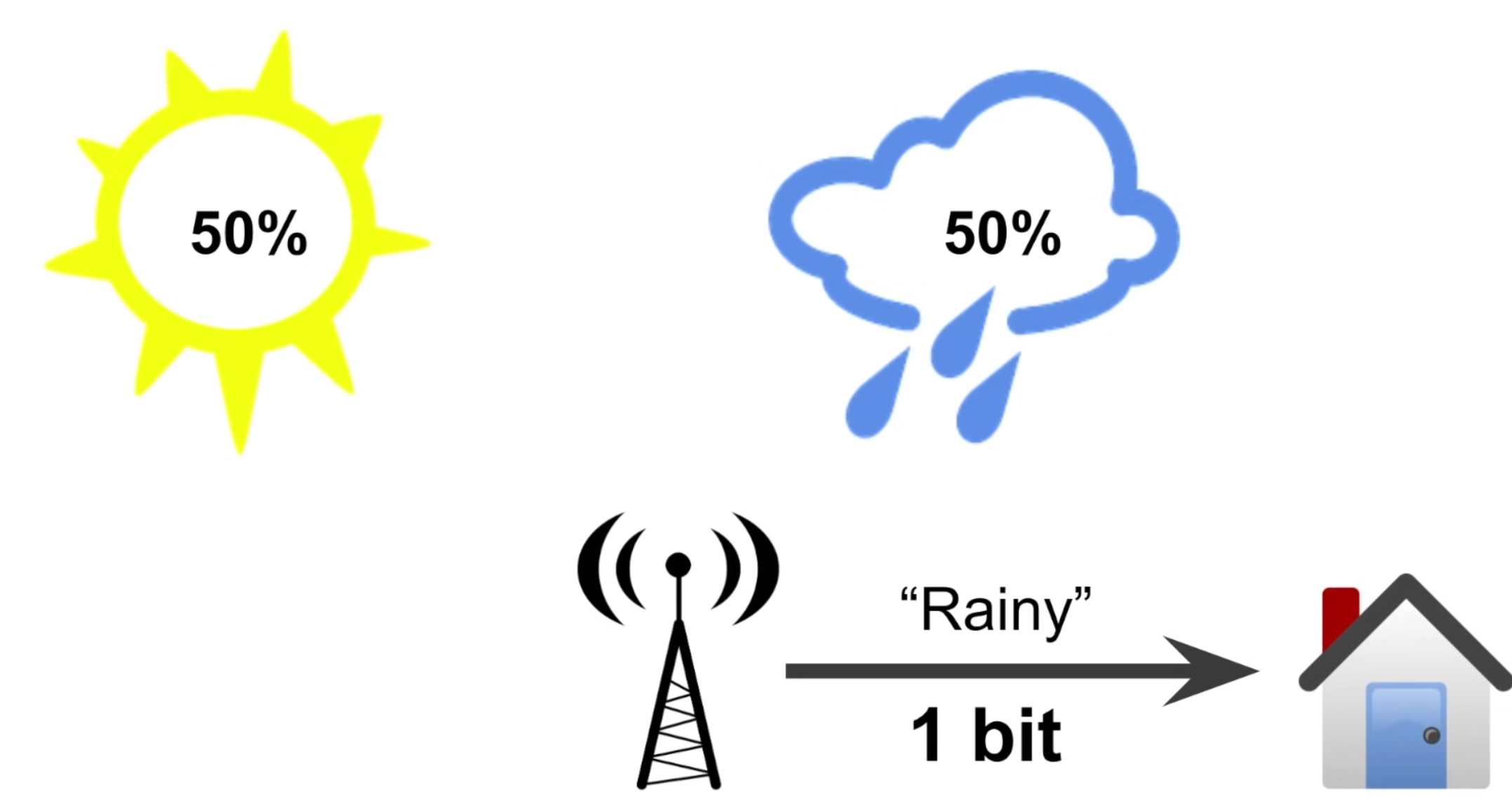
예를 들어 날씨가 50:50의 같은 확률로 맑거나 비가 온다고 가정하면, 기상청에서 비가 온다는 정보를 준다는 것은 위의 두 가지 선택지 (uncertainty) 중 절반인 하나를 선택할 수 있도록 하는 정보를 준 것이다.

이때 기상청은 우리에게 1 bit의 유용한 정보를 전달한 것이다.

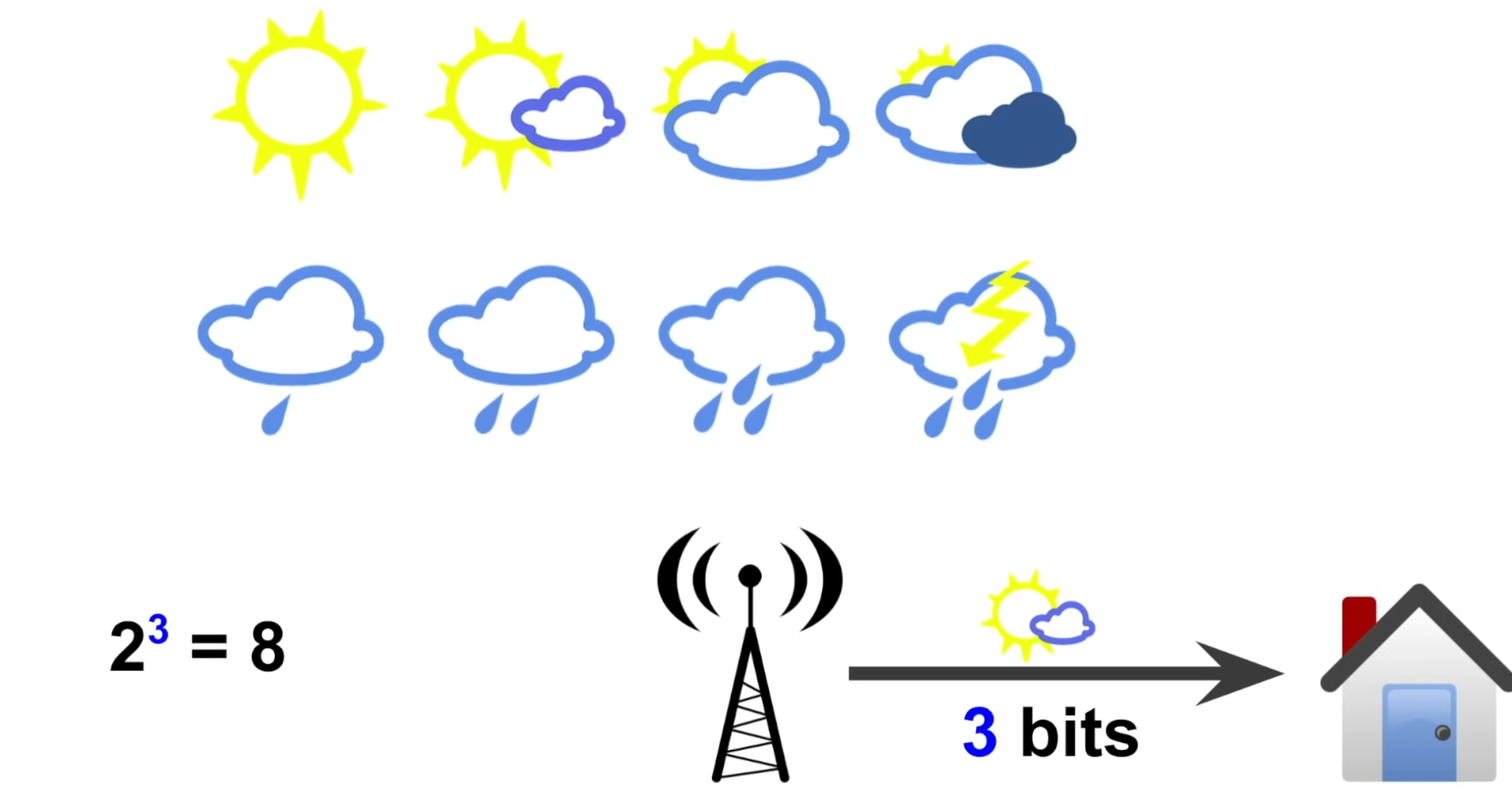
그러면 예를 들어서 날씨가 위의 그림처럼 8가지 경우로 나타난다고 가정하자.

그러면 기상청이 이 중에서 날씨에 대한 정보를 전달한다는 것은, 8가지의 선택지에서 3번 연달아 uncertainty를 줄여준 것으로 볼 수 있으므로, 기상청은 우리에게 3 bit의 유용한 정보를 전달한 것이다.

다르게 생각하면 아래와 같이 날씨를 알아내기 위해 물어야하는 질문의 갯수로도 생각할 수 있다.

질문 1 : 해가 보이나요?
질문 2 : 구름이 많나요?
질문 3 : 구름이 없나요? $\to$ 구름이 조금 있는 맑은 날씨

이를 일반화하면, 정보의 bit 수는 binary logarithm를 계산하여 쉽게 구할 수 있다.

bit=log_2(choices)

그런데, 각 날씨의 확률이 다 똑같지 않게 분포한다면 어떻게 될까?

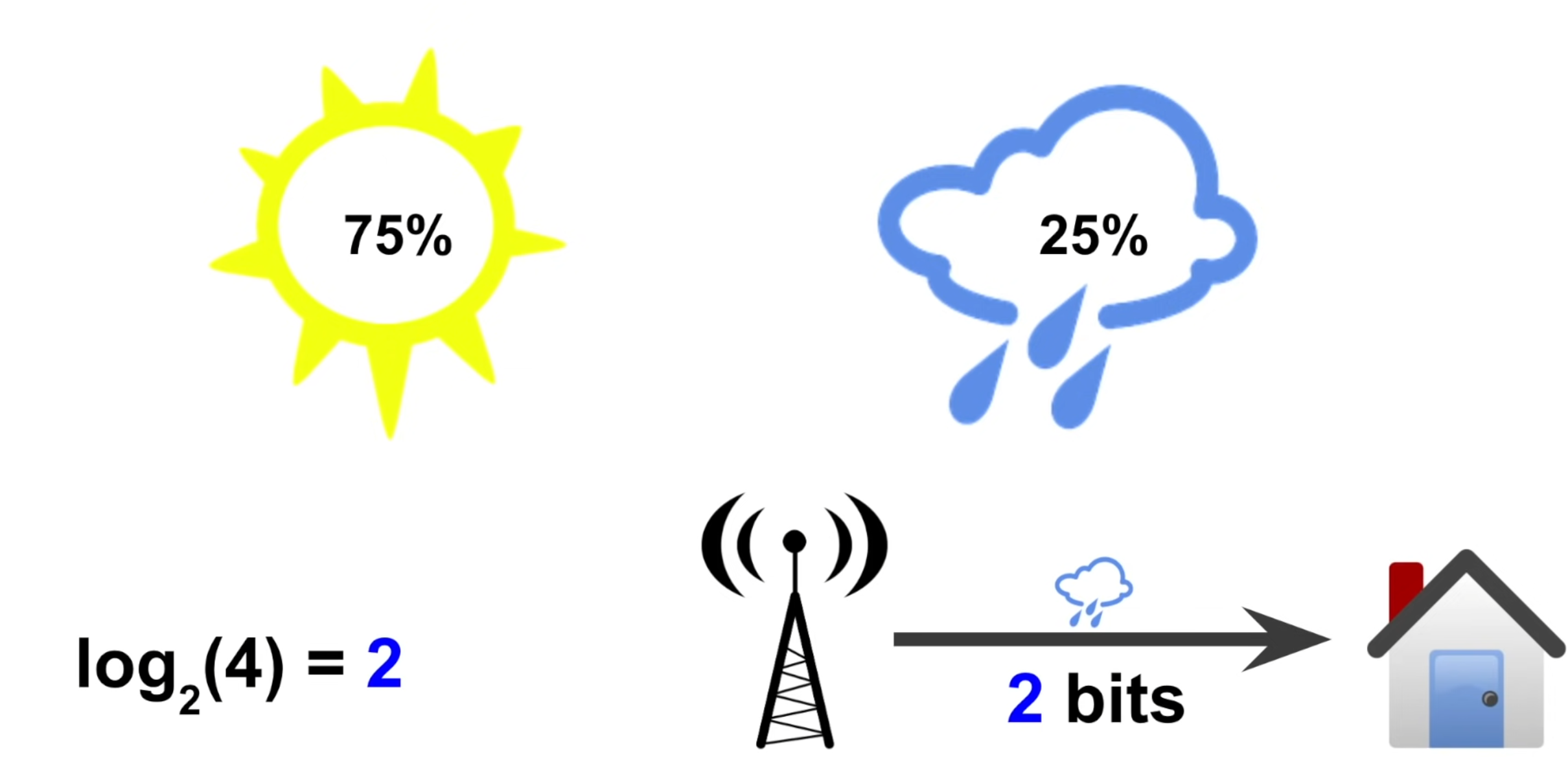
이러한 상황에서 기상청이 내일 비가 온다고 하면, 비가 올 확률이 25%이므로, 우리의 uncertainty는 1/4로 줄어드므로, 2 bit의 정보를 전달한다고 볼 수 있다.

왜냐하면 25%로 비가 온다는 것은 똑같은 확률을 가지는 4 가지 다른 날씨 중에서 하나를 선택한다는 것과 같기 때문이다.

이렇게, uncertainty reduction (uncertainty가 줄어드는 정도)는 해당 사건이 일어날 확률의 역수로 구해지는데, log 표현으로는 마이너스를 붙인 확률의 log로 쓸 수 있게 된다.

bit = -log_2(probability)

반면에, 기상청이 내일 날씨가 맑다고 했다면, 우리의 uncertainty는 그렇게 많이 떨어지지 않으며 정보의 bit 수도 아래와 같이 작다.

bit=-log_2(0.75)=0.41

이는 어찌보면 당연한 것이, 보통 맑은 지역에서는 "내일도 맑습니다."라는 말은 큰 정보가 없는 내용이고 "내일은 비가 옵니다."라는 말은 생각보다 많은 정보를 준다. 그래서 누군가는 정보량을 놀람의 정도라고 표현할 수도 있겠다.

Entropy

그럼 이제 우리가 기상청으로부터 평균적으로 받는 정보가 얼마나 되는지 구해보자.

먼저 내일 날씨가 맑을 확률은 75%인데 이 경우 받는 정보가 0.41 bit이고, 내일 날씨가 비가 올 확률은 25%인데 이 경우 받는 정보가 2 bit이므로, 평균적으로는 매일 $75\% \times 0.41 + 25\% \times 2 = 0.81\; bits$ 의 정보를 받게 된다.

자, 그럼 이제 Entropy를 정의할 수 있다.

Entropy (information theory) https://en.wikipedia.org/wiki/Entropy_(information_theory)
Generally, information entropy is the average amount of information conveyed by an event, when considering all possible outcomes.

Entropy:H(p)=-\sum_ip_ilog_2(p_i)

Entropy는 주어진 분포 ( $p$ )로부터 어떤 sample을 추출하였을 때 얻어지는 평균적인 정보량을 의미하며, 이는 해당 확률 분포가 얼마나 예측하기 어려운지를 나타내기도 한다.

우리가 거의 매일 날씨가 맑은 사막에 살고 있다면, 사실 우리는 기상청으로부터 많은 정보를 받기가 어렵게 되고, 우리나라처럼 날씨가 오락가락인 지역에서는 기상청으로부터 받는 정보가 많을 것이다.

Cross Entropy

Entropy의 개념까지 살펴보았으니 이제 Cross-Entropy에 대해서 알아보자.

Cross-Entropy의 개념은 기본적으로 평균적인 message의 길이를 의미한다.

이게 무슨말인지 한번 아래의 예제를 통해 알아보자.

기상청에서 정보를 전달할때, 아래의 그림과 같이 8가지 선택지에 대해 3-bit encoding를 이용한다고 하자. 그러면 모든 선택지에 대해 평균 message 길이가 3 bits이므로 cross entropy도 3이다.

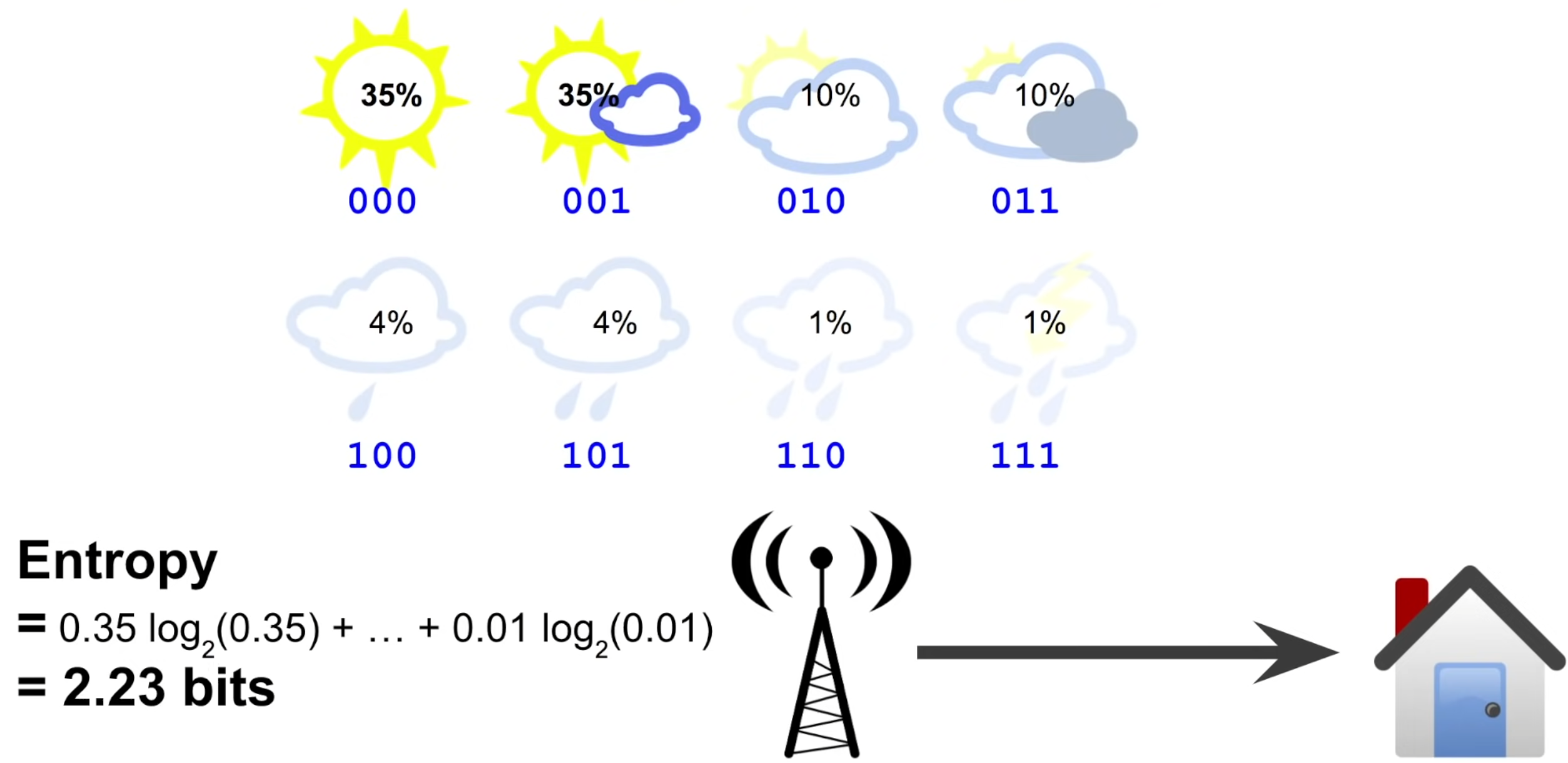
우리가 날이 좋은 지역에 살아서 위와 같이 각 선택지에 대해 확률이 다르다고 가정하면, entropy를 계산해보면 2.23 bits가 나온다.

이 말은 2.23 bits의 정보를 전달하기 위해서 3 bits의 message를 사용하고 있다는 말인데, 이것은 조금 비효율적이다.

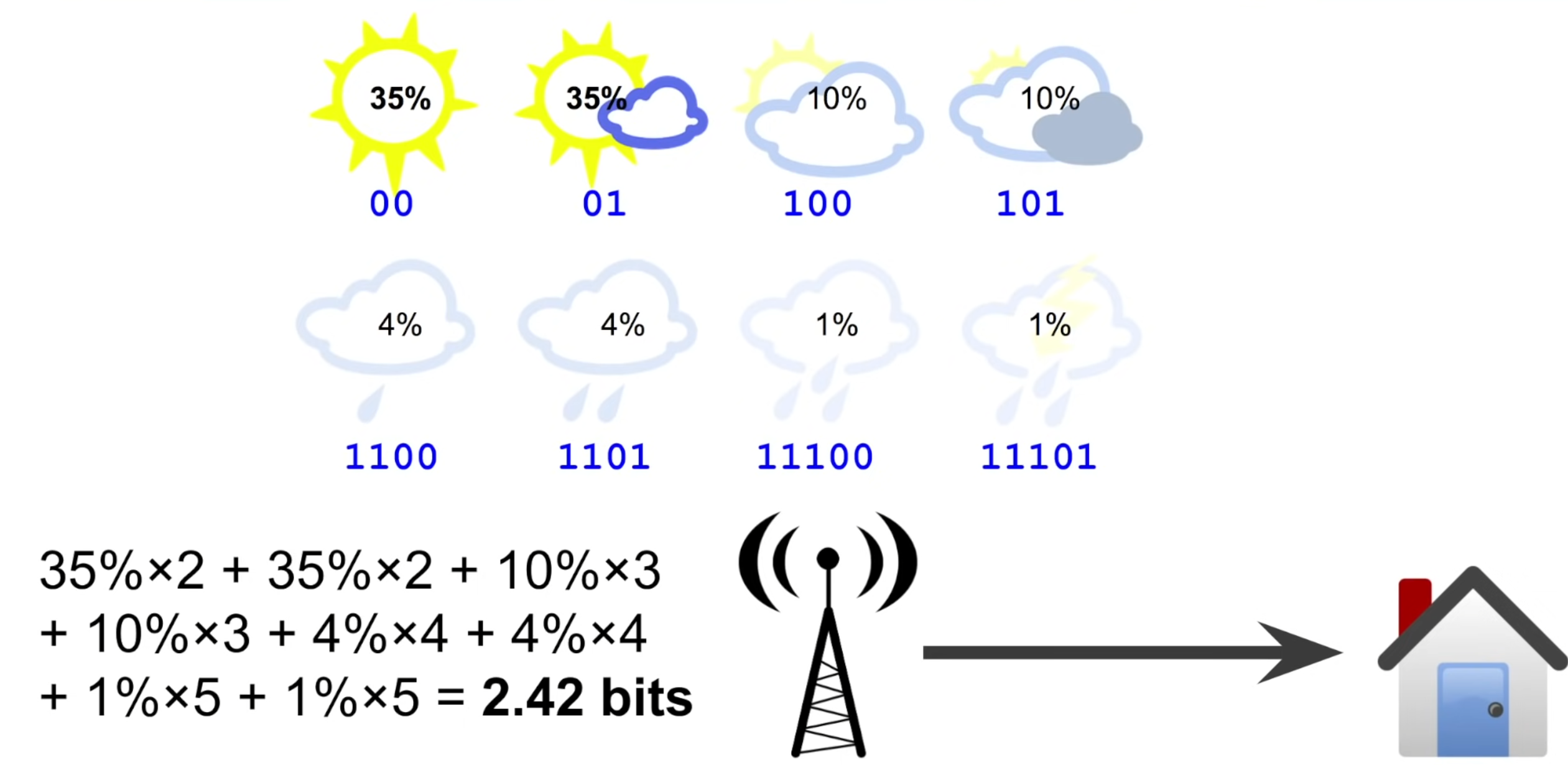
그럼 encoding 방식을 조금 바꿔서, 자주 발생하는 맑은 날씨에는 2 bits, 아주 드물게 나타나는 천둥/번개 날씨는 5 bits를 써보자.

그럼 위의 그림처럼 평균적으로 전달하는 message의 길이 (전달하는 정보의 크기)가 2.42 bits로 줄어드는 것을 확인할 수 있다.

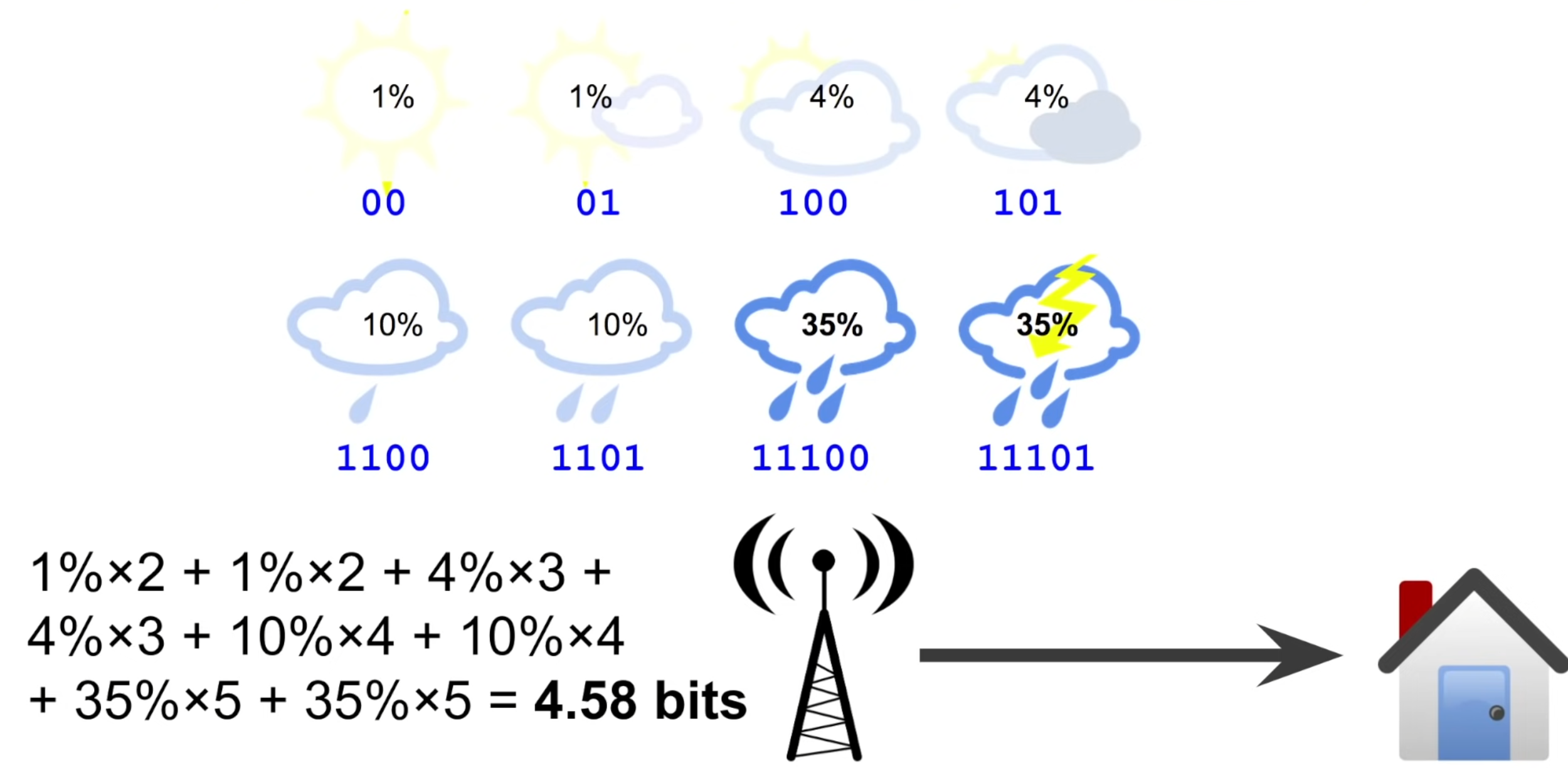
반대로 날이 보통 안좋은 지역에서 같은 encoding을 사용한다고 생각하면, 전달하는 평균 message 길이가 4.58 bits로 매우 커지는 것을 확인할 수 있다.

이렇게 전달하는 평균 message 길이에 차이가 발생하는 이유는 바로 encoding 방식이 weather distribution에 대한 가정을 바탕으로 하기 때문이다.

예를 들어 맑은 날씨를 2 bits로 encoding한 이유는 적어도 25% 확률로 날이 맑을 것이라고 내재적으로 가정했기 때문이다.

2\;bits=-log_2(\frac{1}{4})=-log_2(0.25)

만약에 이 가정이 틀리다면, 우리의 encoding은 최적이 아닐 것이다. 즉, 비효율적으로 정보를 전달하게 될 것이다.

비슷한 방법으로 아래 그림과 같이 내가 예상한 (혹은 가정한) 날씨의 확률 분포를 구할 수 있다.

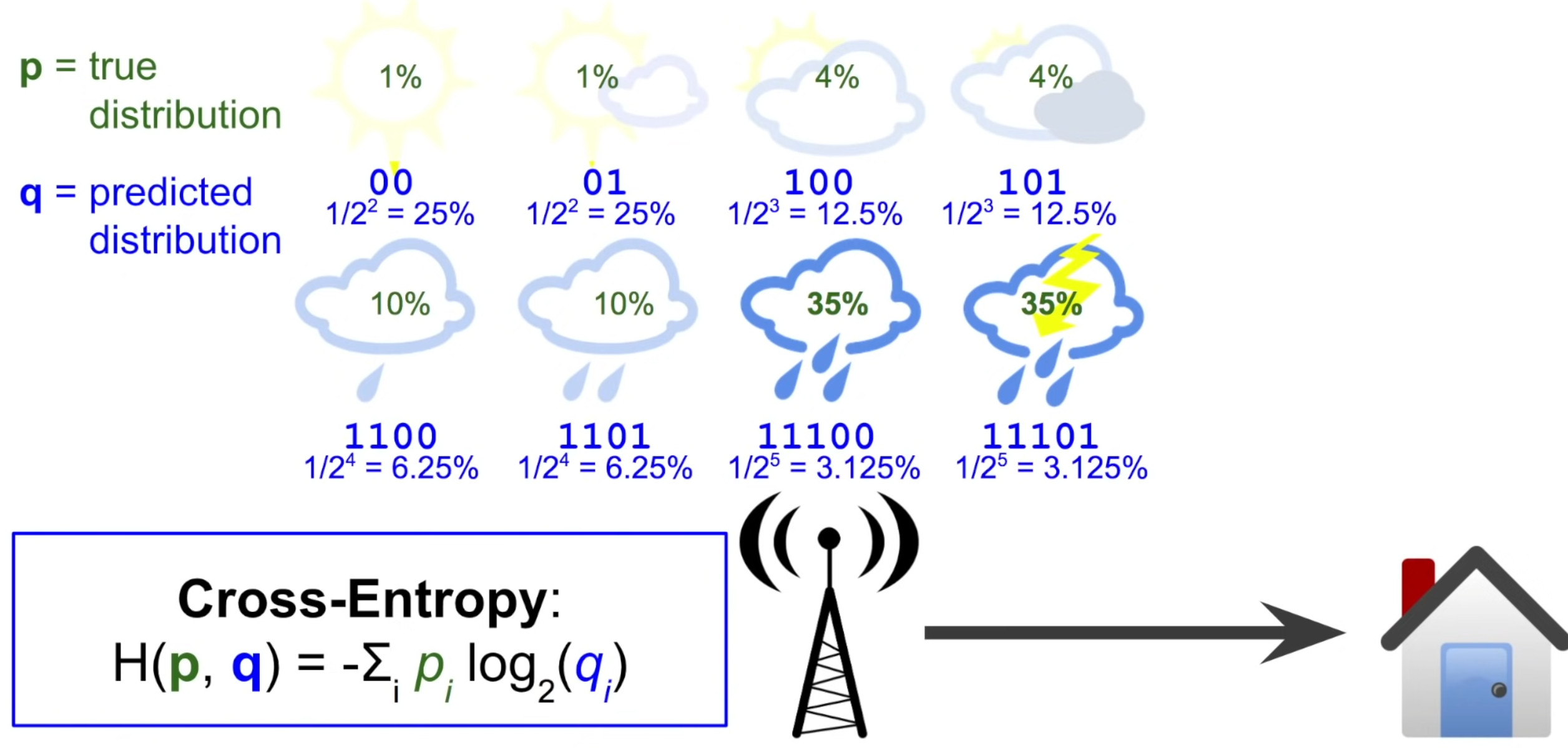
이렇게, 실제 분포와 예측된 분포는 꽤나 다르게 되는데, 여기서 우리는 두 분포 사이의 Cross-Entropy를 정의할 수 있다.

H(p,q)=-\sum_i p_ilog_2(q_i)

식을 보면 예측된 분포에 log을 씌운 후 실제 분포를 곱한 형태로, 이는 전달하는 평균적인 message의 길이 / 정보의 양을 의미한다.

만약 예측이 완전히 정확하다면, predicted distribution과 true distribution이 똑같을 것이고, cross-entropy는 entropy와 값이 같아진다. 반면 예측이 틀리다면, cross-entropy는 entropy보다 큰 값을 갖게 된다.

KL-Divergence

Cross-entropy가 entropy보다 큰 정도를 relative entropy 혹은 KL-Divergence라고 한다.

KL-Divergence는 두 확률 분포의 차이를 계산하는데 사용되는 함수인데, cross-entropy 식으로부터 쉽게 유도된다.

H(p,q)=-\sum_i p_ilog(q_i)

=-\sum_i p_ilog(q_i)\underset{H(p)}{\underline{-\sum_i p_ilog(p_i)}}+\sum_i p_ilog(p_i)

=H(p)+\sum_i p_ilog(p_i)-\sum_i p_ilog(q_i)

=H(p)+ \underset{KL-Divergence}{\underline{\sum_ip_ilog\frac{p_i}{q_i}}}

정리해서 KL Divergence는 Cross-Entropy에서 Entropy를 뺀 값이다.

D_{KL}(p||q)=H(p,q)-H(p)

보통 $H(p)$ 는 상수로 고정되기 때문에, Cross-Entropy를 minimize한다는 것은 KL-Divergence를 minimize한다는 것과 동치이며, 두 확률 분포의 차이를 최소화한다는 것으로 생각할 수 있다.

Usage

Deep network의 classifier를 학습시킬때 Cross-Entropy를 많이 쓰게 된다.

특히 PyTorch의 경우,

1) Multi-class classification
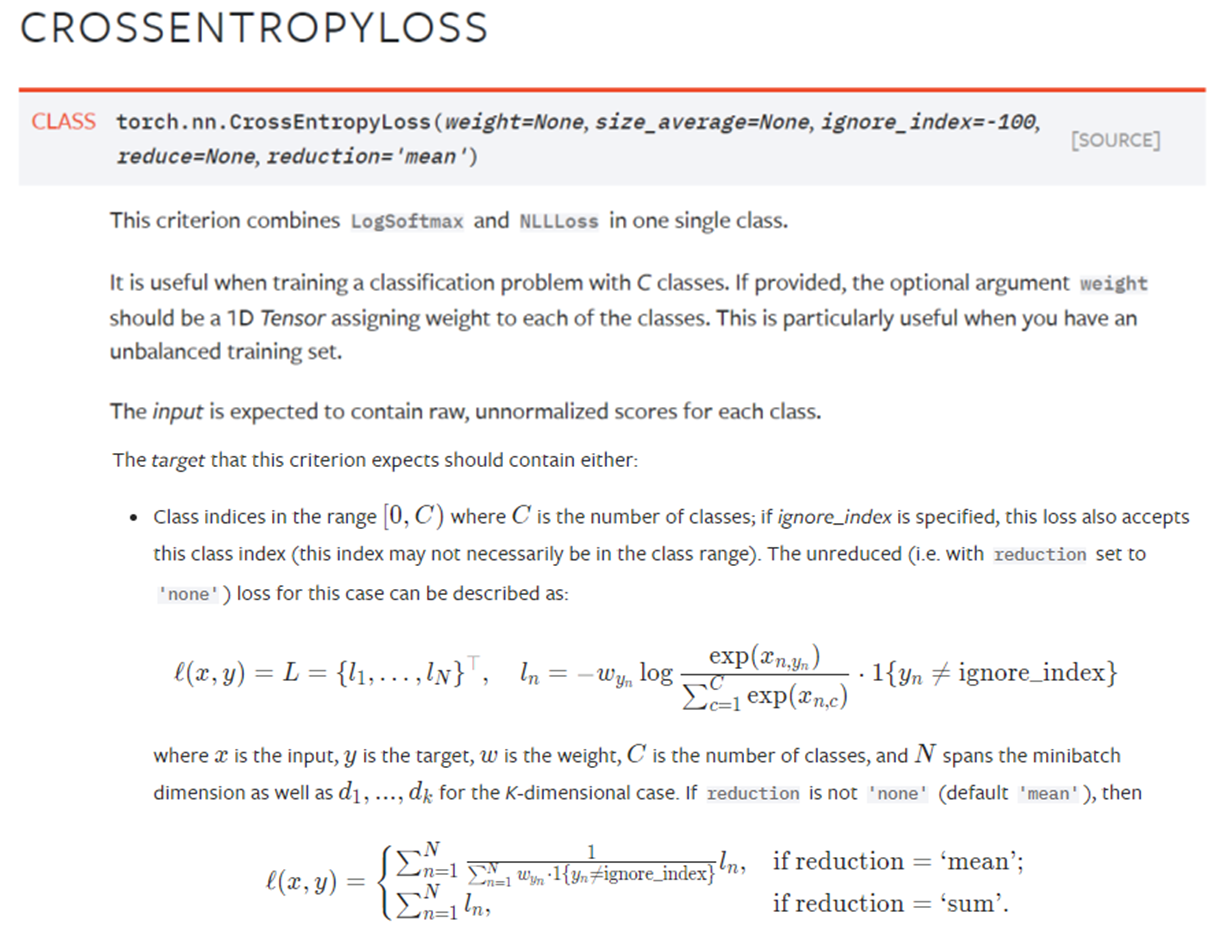
Multi-class classification에서는 torch.nn.CrossEntropyLoss를 주로 사용한다.

이 loss function은 LogSoftmax와 NLLLoss를 합쳐 사용한 것으로, network output에 softmax를 취하고, negative log를 취한 것을 loss로 사용한다.

Softmax는 하나의 image에 대해 나온 output에서 적용되며, 단 하나의 class만 큰 값을 갖도록 유도한다고 볼 수 있음

2) Multi-label classification
Multi-label classification에서는 torch.nn.BCEWithLogitsLoss를 주로 사용한다.

이 loss function은 Sigmoid와 BCELoss를 합쳐 사용한 것으로, network output에 sigmoid를 취한 후, 각각 label마다 binary cross entropy를 구한다.

Binary classification의 경우 C-개의 class가 각각 0 혹은 1의 $y$ 값을 가지게 된다.

BCELoss=-ylog\hat{y}-(1-y)log(1-\hat{y})

BCE Loss를 minimize하도록 학습한다는 것은,,

$y=1$ 이면 두번째 항이 사라지므로 $-log\hat{y}$ 를 minimize, 즉 예측값 $\hat{y}$ 을 maximize해야함
$y=0$ 이면 첫번째 항이 사라지므로 $-log(1-\hat{y})$ 를 minimize, 즉 예측값 $\hat{y}$ 을 minimize해야함

Training의 관점에서...

출처 : Distribution-Balanced Loss for Multi-Label Classification in Long-Tailed Datasets

CE와 BCE는 보통 적용되는 task자체가 다르긴 하다. CE는 one-hot label classification에서 주로 사용되고, BCE는 multi-label classification에서 주로 사용된다.

하나의 example에 대해 CE는 output 전체에 softmax를 적용하여 각 class output끼리의 mutual exclusion을 강조하는 반면, BCE는 output의 각각 class에 따로 sigmoid를 적용하고 독립적으로 계산한다.

그래서 optimization의 관점에서 봤을 때 negative example에 대한 gradient를 조금 생각해보는 것도 재미있는 일이다.

간단하게 각각 loss의 gradient를 계산해보면 아래와 같다. (loss 수식은 위 pytorch document의 $l_n$ 을 참고하고, 이를 output $x$ 로 미분했다고 생각하면 된다. $j$ 는 해당 class index)

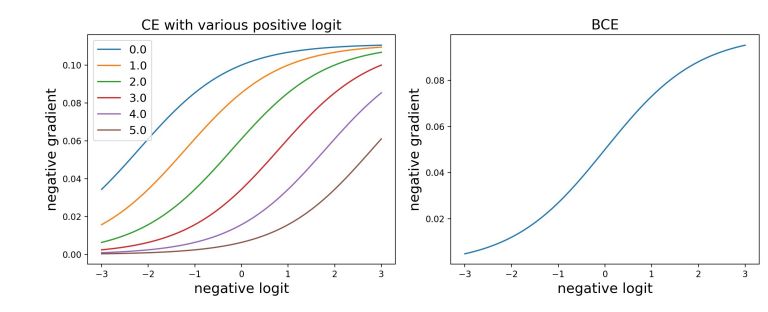
\frac{\partial\mathcal L_{CE}(x_j,y)}{\partial(x_j)}=\frac{e^{x_j}}{\sum^C_{i=0}e^{x_i}},\;y_j=0

\frac{\partial\mathcal L_{BCE}(x_j,y)}{\partial(x_j)}= \frac{1}{C}\frac{e^{x_j}}{1+e^{x_j}},\;y_j=0

Softmax의 경우 다른 class의 output에 영향을 받으므로, 만약에 positive class $y_{k \neq j}$ 의 output이 충분히 크다면, gradient가 어느정도 작게 형성되는 것을 볼 수 있다. 반면에 sigmoid의 경우 다른 class에 관계없이 독립적으로 output을 0 또는 1로부터 멀도록 하기 때문에, negative example에 대한 영향이 더 크다고 볼 수 있다.

Multi-label classification의 경우 각 class의 classifier 입장에서 negative example이 훨씬 많으므로 network 학습 시 negative example에 대해 over-suppression 현상이 발생할 수 있다. (negative example에 대해 너무 confident해서 계속 0에 가깝게 값을 도출)

이런 경우 갯수가 적은 tail class의 경우 모델이 아주 적은 positive example에 over-fitting하게 된다.

특히 class distribution이 imbalance한 상황에서는 minor class에 대해 문제가 더욱 심각해지므로 주의할 필요가 있다.