Learned Initializations for Optimizing Coordinate-Based Neural Representations 리뷰

신희준·2023년 8월 26일

Paper Review

목록 보기

9/30

Paper : Learned Initializations for Optimizing Coordinate-Based Neural Representations (TLearned Initializations for Optimizing Coordinate-Based Neural Representations / CVPR 2021)

NeRF 본 논문의 저자가 쓴 논문이다.

Motivation: NeRF는 training view image도 많이 필요하고, training time도 많이 소요가 되는 단점이 있는데, 이러한 단점을 해결할 수 있는 방법을 찾고 있었다.

Test time optimization task인 NeRF 학습에 간단한 방법으로 prior를 잘 부여하여 학습 속도를 개선시키고

Short Summary

Meta-learning algorithm을 NeRF training에 도입하여 initialization weight를 최적화
간단한 implementation으로 strong prior를 부여하여 NeRF training convergence와 generalization 성능을 향상

Introduction

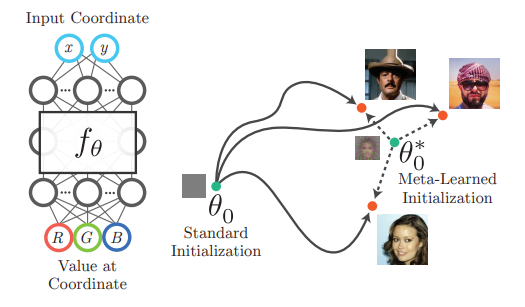
NeRF와 같은 coordinate-based neural representation model은 어떤 input coordinate를 입력으로 받고 그 coordinate의 signal을 출력한다.

이러한 모델들은 3D voxel에 discrete하게 값을 저장하는 방식이 아니라서 continuous하고 memory efficient한 장점이 있다.

하지만 neural representation을 최적화하는데는 보통 많은 gradient descent step이 필요하다. 특히나 NeRF는 test-time optimization 방식을 사용해서 매번 from-stratch로 학습하는 것은 매우 비효율적이다.

이 논문에서는 이런 문제를 해결하기 위해 meta-learning을 활용하여 initialization weight를 학습하는 방식을 제안하였고, 학습된 initialization weight는 특정 3D scenes이나 volumetric data를 표현하는 강력한 prior knowledge로 작용하여 test-time optimization 시 convergence 속도를 향상시키고, fewer observation에 대해서도 더 나은 generalization 성능을 보여줬다고 한다.

Meta-learning 방법으로는 가장 유명한 optimization-based meta learning인 MAML과 Reptile을 사용하였으며, 기존의 neural representation training에서 outer loop만 추가하여 meta-model을 학습시키고, 학습이 끝난 후부터는 learned initial weight를 매번 새로운 signal을 encoding할 때, pretrain weight처럼 불러와서 학습을 하면 된다.

Meta-learning

Meta learning은 일반적으로 few-shot learning 문제를 해결하기 위한 방법론으로, training을 하는 동안은 접하지 못했던 새로운 task에 대해서 빠르게 잘 적응하도록 모델을 학습하는 learning-to-learn concept의 학습 방법이다.

이 논문에서는 optimization-based meta learning 방식인 MAML과 Reptile 방법을 차용하였다. 두 방법 모두 inner model과 outer meta model을 정의하고, inner model의 optimization result를 outer meta model에 반영하여 최적의 initialization weight를 찾는 방식이다.

OpenAI의 On First-Order Meta-Learning Algorithms (Alex Nichol, Joshua Achiam, John Schulman)에서 자세한 설명을 공부해볼 수 있겠다.

Method

먼저 signal $T$ 를 bounded $d$ -dimensional cooridnates $x\in C \in \mathbb R^d \to \mathbb R^n$ 으로 mapping하는 함수라고 정의하자. (예를 들어서 NeRF에서 $T$ 는 3d location을 4D tuple (color & density)로 mapping하는 함수)

그리고 우리는 coordinate-based neural representation $f_\theta$ 를 최적화하여 모든 coordinate에 대해 $T$ 와 최대한 가깝게 학습한다.

만약에 signal $T$ 에 대한 pointwise observation ( $\{(x_i,T(x_i)\}_i$ )이 주어진다면 $f_\theta$ 는 L2 loss를 이용한 gradient descent 방식으로 학습이 가능하다. (learning rate $\alpha$ )

L(\theta)=\sum_i||f_\theta(x_i)-T(x_i)||^2_2

\theta_{i+1}=\theta_i-\alpha\nabla_\theta L(\theta)|_{\theta=\theta_i}

Adam과 같은 optimizer를 사용해서 gradient moment를 지속적으로 tracking하여 optimization trajectory를 잘 맞춰줄수도 있다.

$m$ 번의 optimization step이 지난 후, 서로 다른 initial weight $\theta_0$ 를 이용하면 서로 다른 최종 weight $\theta_m$ 를 얻을 수 있을 것이다.

반면에 signal $T$ 에 대한 indirect한 observation ( $M(T,p)$ )만이 주어지는 경우가 있다. (NeRF에서 카메라 포즈 $p$ 에 대한 2D captured image가 주어지는 경우)

이 경우 forward model $M$ (volume rendering 등)을 활용하여 학습하는 inverse problem을 풀게 된다.

L_M(\theta)=\sum_i||M(f_\theta,p_i)-M(T,p_i)||^2_2

이때 forward model $M$ 이 너무 많은 정보를 잃어버리거나, $\{(p_i,M(T,p_i)\}_i$ 의 수 자체가 너무 적다면, $T$ 에 가깝게 학습하기가 어려울 것이다. 그래서 보통 NeRF는 적은 수의 view image로 학습하면 결과가 안좋다.

Optimizing initial weights

위에서 observation을 이용해 singal $T$ 를 학습하는 방법을 간단하게 설명하였다.

그런데, 만약에 임의의 $T$ 를 포함하는 특정 분포 $\mathcal T$ 에 대한 데이터셋이 있다고 했을 때 (여러 개의 CT volume과 해당 volume의 projection images?), 각각의 $f_\theta$ 를 from stratch에서 학습하지않고, common한 prior knowledge를 가지고 좀 더 잘 학습해볼 수 있지 않을까?

이 논문에서는 $f_\theta$ 를 같은 distribution의 unseen signal에 대해서 $f_\theta$ 를 학습할 때, 최종 $L(\theta_m)$ 을 최소화하는 어떤 최적의 initial weight $\theta_0^*$ 를 찾으려고 한다.

\theta^*_0=argmin_{\theta_0}E_{T\sim\mathcal T}[L(\theta_m(\theta_0,T))]

MAML & Reptile

두 가지 optimization-based meta learning 방법은 여러 task distribution $\mathcal T$ 에서 임의의 $T_j$ 를 추출하여 inner loop를 학습하고, 이 inner loop의 $m$ 번의 optimization 결과를 통해 outer loop의 meta model을 학습한다.

MAML은 gradient descent를 통해 weight를 update하고, Reptile은 second-order gradient를 계산하지 않는 간단한 update rule을 사용한다.

MAML
$\theta^{j+1}_0=\theta^j_0-\beta\nabla_\theta L(\theta_m(\theta,T_j))|_{\theta=\theta^j_0}$
Reptile
$\theta^{j+1}_0=\theta^j_0-\beta (\theta_m(\theta^j_0,T_j)-\theta^j_0)$

Reptile은 단순히 task-optimized weight의 방향으로 이전 weight initialization을 옮겨놓는다. 이 논문에서는 MAML보다 Reptile이 더 memory efficient하기 때문에 더 많은 inner loop optimization step을 가질 수 있고, 실험적으로 complex task일수록 더 많은 optimization step이 효율적이기 때문에 이 경우 Reptile을 사용했다고 한다.

아래는 Reptile algorithm이다.

PyTorch code로는 아래와 같이 간단히 표현될 수 있을 것이다.


meta_model = mymodel()
meta_optim = torch.optim.Adam(meta_model.parameters(), meta_lr)

for epoch in meta_epoch:
  meta_optim.zero_grad()

  inner_model = copy.deepcopy(meta_model)
  inner_optim = torch.optim.SGD(inner_model.parameters(), inner_lr)
  
  # training and update inner model
  do_training(inner_model, inner_optim)
  
  # replace gradient of meta_model with the update of inner model 
  with torch.no_grad():
  	for meta_param, inner_param in zip(meta_model.parameters(), inner_model.parameters()):
    	meta_param.grad = meta_param - inner_param
  
  meta_optim.step()

Results

2D image regression, 2D CT reconstruction, 3D object reconstruction, 3D scene reconstruction 등 여러 가지 task에 대해서 실험을 진행하였다.

각각의 task에 대해 여러 initialization scheme에 대한 test-time optimization 결과를 보여주었다.

(1) Standard: Standard random initialization
(2) Mean: Optimize network to match the mean signal of $\mathcal T$
(3) Matched: Optimize network to match the meta-learned initialization for $\mathcal T$
(4) Shuffled: Permute the weights (within each network later) of meta-learned initialization

여기서 Mean은 signal space에서 good initialization 을 의미하고, Match는 weight space에서 good initialization을 의미한다. Shuffled는 statistical distribution이 meta-learned initialization과 matching되는 경우이다.

Faster convergence

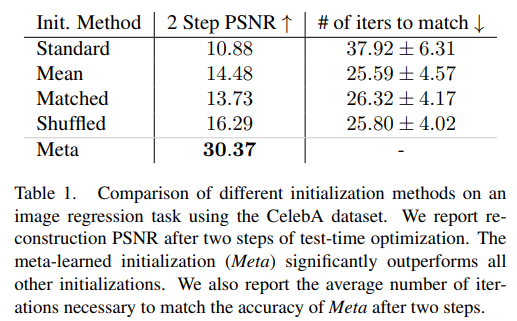
2D image regression에서 Meta learned initialization은 2 step만에 거의 완벽한 이미지를 만들어낼 수 있는 반면에 다른 baseline initialization method들은 비슷한 성능을 내기 위해 10배가 넘는 iteration이 필요했다고 한다.

신기하게도 face image로 Meta-learned된 initial weight가 다른 natural image에서도 학습 속도 향상에 도움을 줬다고 한다.

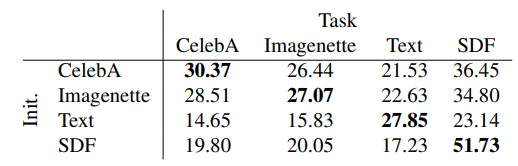
물론 각각 task에 맞는 meta-initialize를 해주었을 때 최고의 performance가 나온다고 한다.

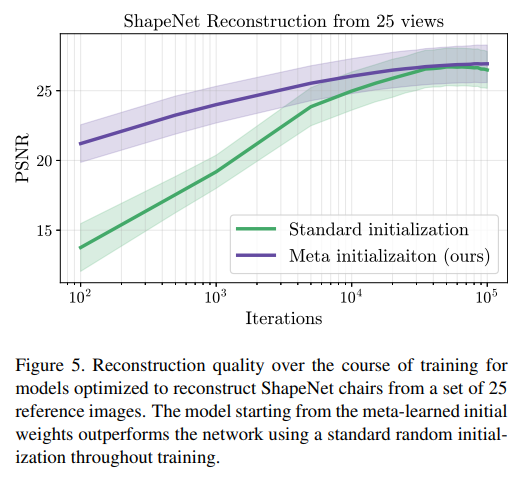
View synthesis task에서도 25view를 이용했을 때, 학습 속도가 매우 빠른 것을 확인할 수 있었다. 하지만 최종적인 recon quality는 비슷했다.

Generalizing from partial observations

학습 속도 뿐만 아니라, 더 적은 input으로도 비슷한 결과를 낼 수 있게 됬다고 한다.

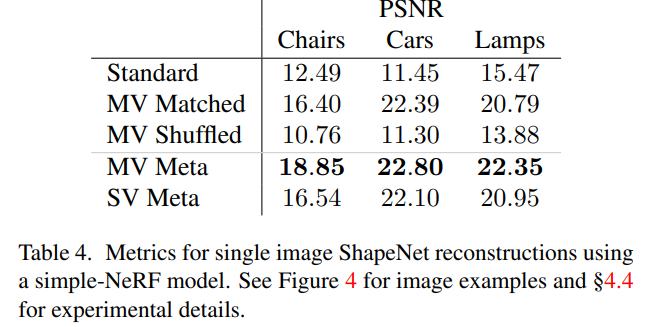
위의 결과는 single view를 이용한 NeRF reconstruction의 결과이다. standard method는 당연하게도 유의미한 결과를 만들어내지 못한 반면에, Meta learned initialization을 사용했을 때는 한 개의 view로도 적당한 결과를 만들어낼 수 있었다.

(SV는 meta-learning도 single view로 한 것, MV는 meta-learning에서 multi view를 이용한 것)

Discussion

예전에 few show classification 분야에서 meta-learning을 사용하는 것을 몇 번 봤는데, Coordinate-based network에 잘 결부시켜서 좋은 결과를 얻은 것 같다.

Meta-learning이든 transfer learning이든지 pretrained network를 이용해서 prior를 부여하고 training 자체나 generalization performance를 향상시키는 연구들은 자연스럽고 합리적인 발전 방향이라고 느껴진다.

개인적으로는 fast convergence에 관한 부분은 아주 직관적으로 이해가 가는데, fewer input으로 좋은 결과를 내는 데에는 무언가 더 필요하지 않을까 싶었다. 비슷한 dataset에 대한 prior를 부여했다고 해도 결국에는 해당 scene에 대해서 완벽하게 recon을 해내려면 fine detail을 학습할만한 충분한 정보가 필요할 것이라 생각이 된다.

1 shot training으로는 standard initialization이랑 상당한 차이를 내지만, 3 shot, 5 shot, 10 shot으로 늘려가면서 meta learning이 실제로 같은 정보를 가지고서 얼마나 더 잘 recon을 해낼 수 있을 지에 대한 결과가 궁금해졌다.