Least square method

우리는 error를 최소화 해야 할 필요가 있다! 그래서 가장 첫번째로 등장하는 방법이 LSE, Least Square Method이다.

Least square는 위와 같이 나타낼 수 있다. 즉 $Y_i$에서 $E(Y)$를 제해준 값으로, random error term을 의미하기도 한다.

그리고 그냥 값이 아닌 제곱을 하는 이유는 음수의 오차와 양수의 오차를 더했을 때 값이 상쇄되는 효과가 일어난다. 또한 절댓값을 사용하지 않는 이유는 최솟값을 구할 때 미분을 사용하지 못하기 때문이다.

Q. 그렇다면 최적의 $\mathit{\beta}_0 ,\mathit{\beta}_1$ 값은?
A. 편미분하면 된다!

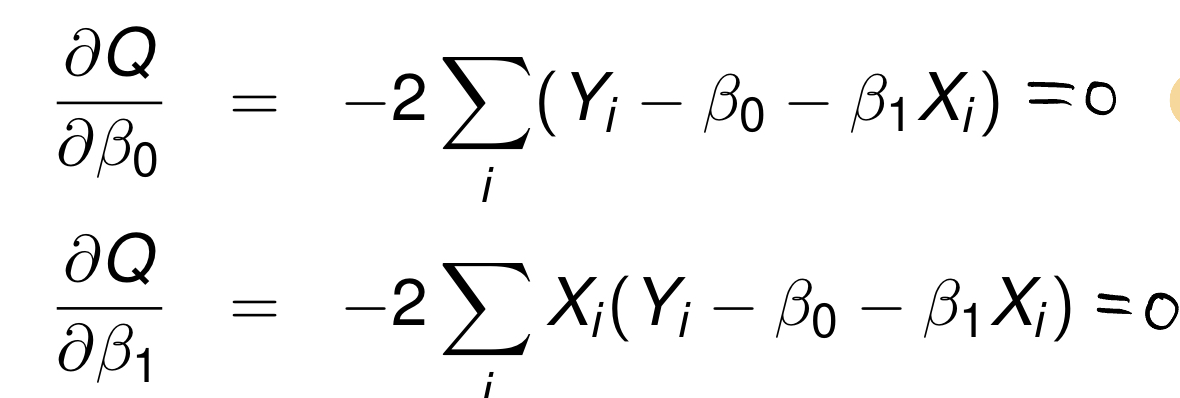
위와 같은 식을 우리는 정규방정식, normal equation 이라고 한다.

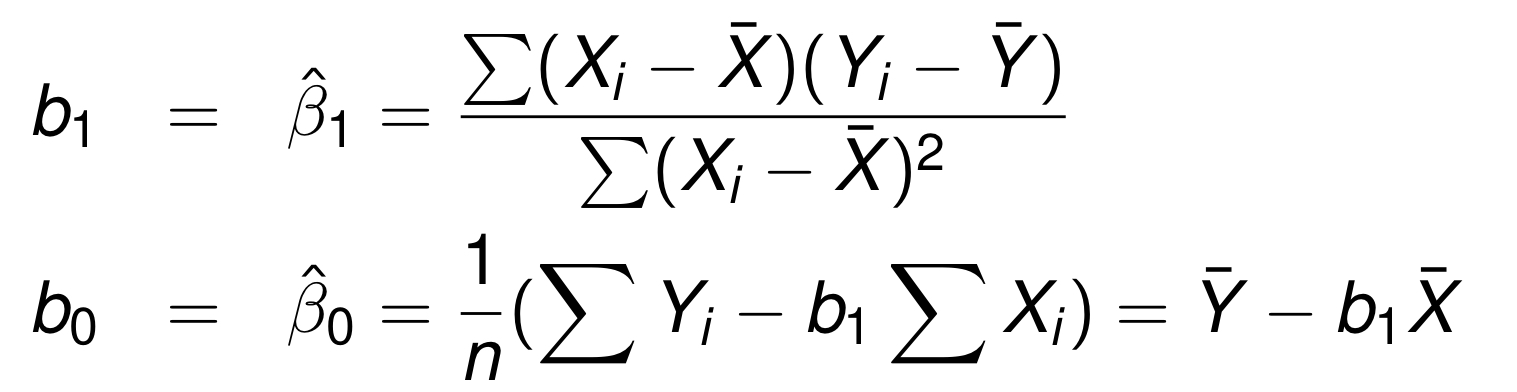
정규방정식을 풀면 다음과 같이 계수를 추정할 수 있다.

Gauss Markov Theorem

그렇다면 least square method로 얻은 것이 합리적인지, good approach인지 알아야 한다. 이 부분은 수업시간에 증명하지 않았지만 나중에 한번 읽어보기 위해 위키 링크를 미리 첨부해둔다.
https://en.wikipedia.org/wiki/Gauss%E2%80%93Markov_theorem
그리고 이 theorem에 따르면 우리가 LSE로 추정한 계수가 BLUE임을 알 수 있다. (best linear unbiased estimatiors)

Residual

그렇다면 이제 구분이 필요하다.

$E(Y) = \mathit{\beta}_0 +\mathit{\beta}_1X$
$\hat{Y} = b_0+b_1X$

$\hat{Y}$는 regression을 통해 추정된 회귀계수를 이용해 나타낸 식이다. 이제 이것을 fitted 라고 칭할 것이다.

Residual VS Random error

residual 은 실제 값에서 추정 값을 제외한 것이고, error term과는 엄연히 다름을 확실히 해야한다. Random errorsms 실제 값에서 평균값을 제외해준 값이다. 식으로 표현하면 다음과 같다.
Residual : $e_i = Y_i. - \hat{Y_i}$ (실제값 - 추정값)
Random error : $\mathit{\epsilon}_i = Y_i- E(Y_i)$ (실제값 - 평균값)

properties of fitted regression line

1. residual의 합은 0이다.
2. squared residual의 합은 최솟값이다.
3. $Y_i$의 합과 $\hat{Y_i}$의 합은 동일하다.
4. 추정된 regression line은 항상 $(\bar{X}, \bar{Y})$를 지나간다.

용어 정리

$e_i = Y_i - \hat{Y_i}$ 는 residual
SSE = $\sum_{i}(Y_i-\hat{Y})^2= \sum_{i}(\mathit{\epsilon}_i)^2$
MSE : mean squared error, SSE를 degree free (자유도)로 나누어준 값이다. linear regression에서는 자유도가 n-2이다. 2는 추정해야하는 회귀계수를 제외해준 것이다.
$s^2 = MSE = SSE/(n-2)$
$E(MSE) = \mathit{\sigma}^2$
(여기서 $s^2$은 unbiased estimator)

Normal Error Regression model

위에서 같이 error가 정규분포를 따른다고 가정하자.
즉
$E(\mathit{\epsilon}_i) = 0$
$Var(\mathit{\epsilon}_i) = \mathit{\sigma}^2$
$Cov(\mathit{\epsilon}_i,\mathit{\epsilon}_j) =0$
이다.

---

to be continued..