회귀 분석

계절학기로 회귀분석을 수강하게 되었다! 사실 전에 대충 공부해봤어서 뭐하는건지는 정말 정말 조금 알고 있었는데, 학교에서 수업으로 들으니까 약간 물음표들이 정리되는 기분이었다. 솔직히 어려운 과목인거 진짜 맞고,많은 양을 한번에 머릿속에 넣으려니 힘들기도 했지만 나름대

우리는 error를 최소화 해야 할 필요가 있다! 그래서 가장 첫번째로 등장하는 방법이 LSE, Least Square Method이다.$$Q=Q(\\mathit{\\beta}0 ,\\mathit{\\beta}\_1 ) = \\sum{i}(Y_i-\\mathit{\\b

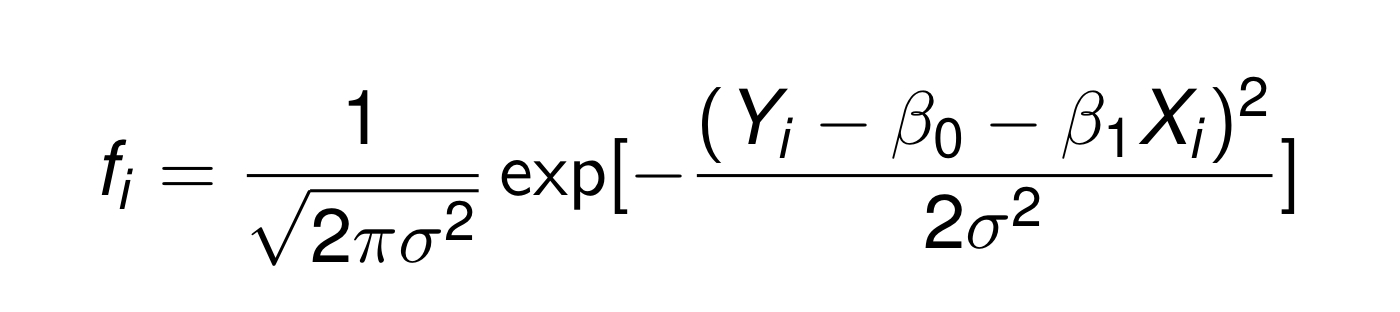
likelihood는 한국말로는 우도라고 한다. (제주도 우도 땅콩 막걸리 맛있음) 조금 더 풀어서 설명하자면, 우리가 직접 관측한 데이터가 우리에게 주는 값이라고 생각하면 된다. 예시10번 동전을 던졌고, 8번의 head가 나왔다면 이러한 정보에 근거해서 우리는 he

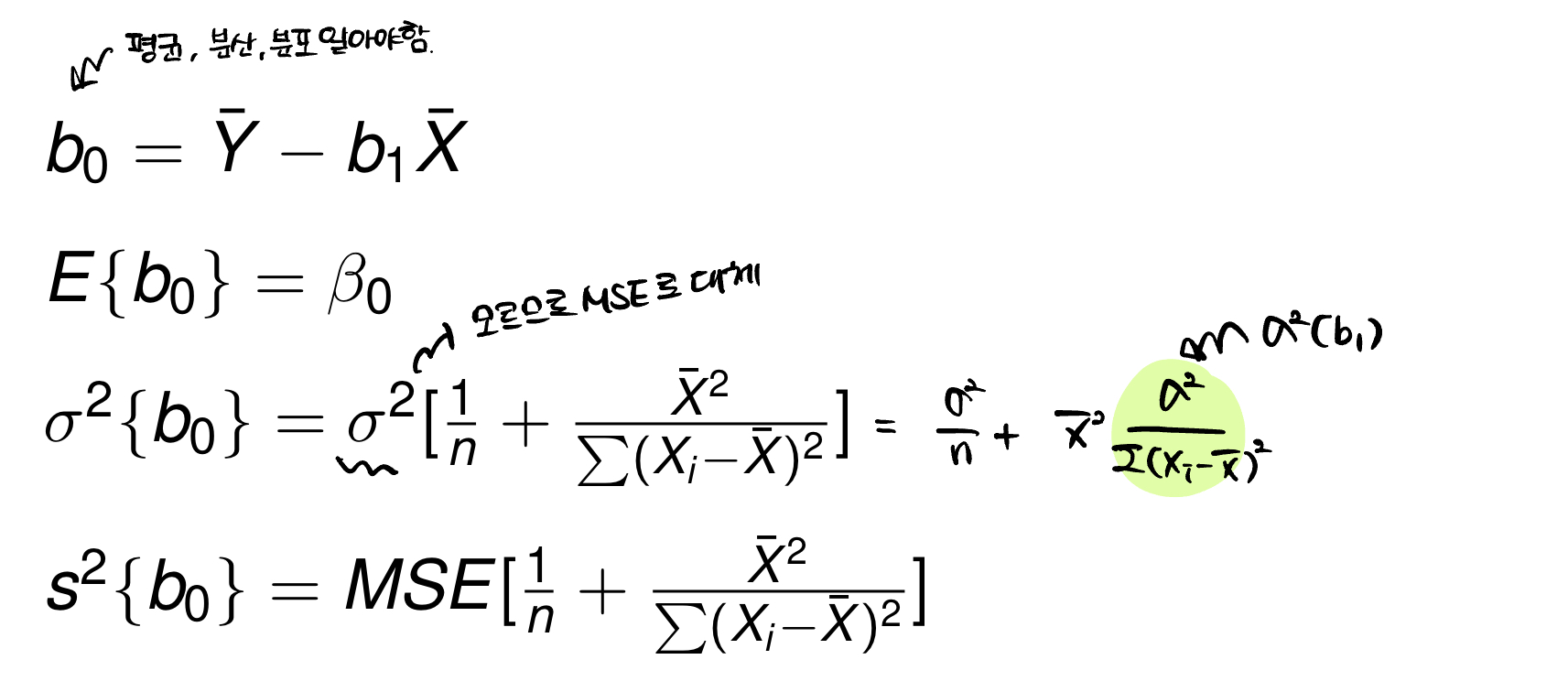
Statistical inferece란.. 데이터 분석 과정을 통해 분포의 특성을 추론하는 과정이다. 가설을 testing하고, 모수를 추정한다. Normal linear regression model $$ Yi = \mathit{\beta}0 + \mathit{\

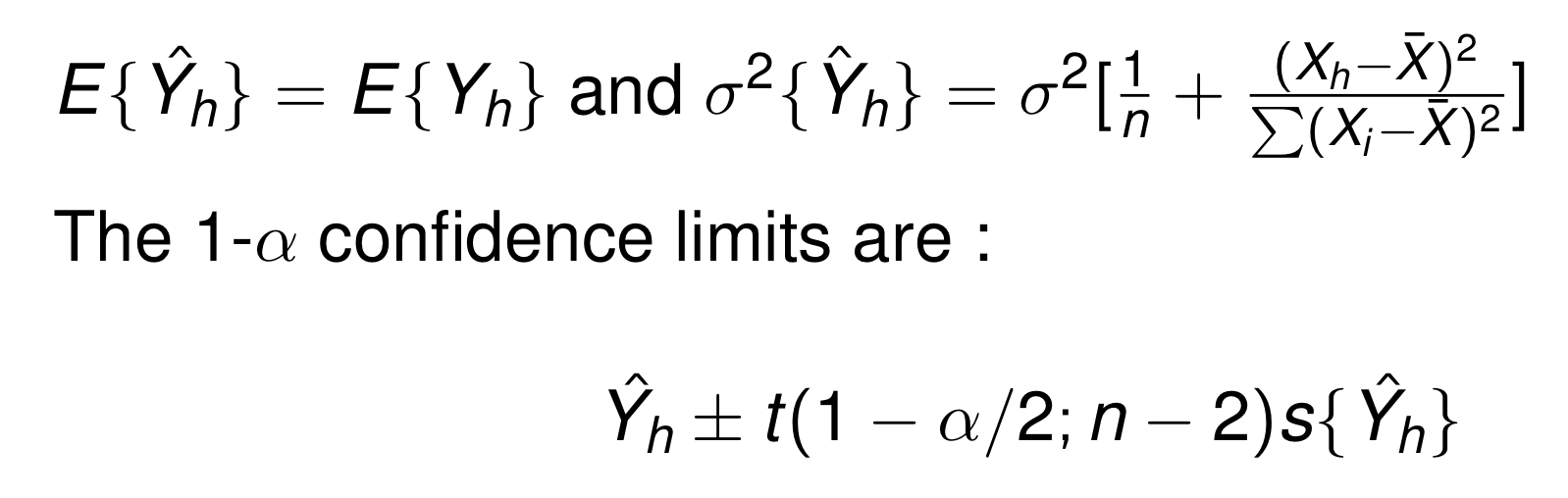
(1) 번 포스트에서는 회귀계수의 추정값에 대해서 다루었다.그렇다면 $\\hat{Y}\_h$의 estimation에 대해 알아보자.절대 TeX문법 쓰기 귀찮아서 이미지로 자꾸 첨부하는 것 아니다.기댓값에 대해서는 기존의 선형 회귀 식을 생각해서, 그 자체에 기댓값을 씌

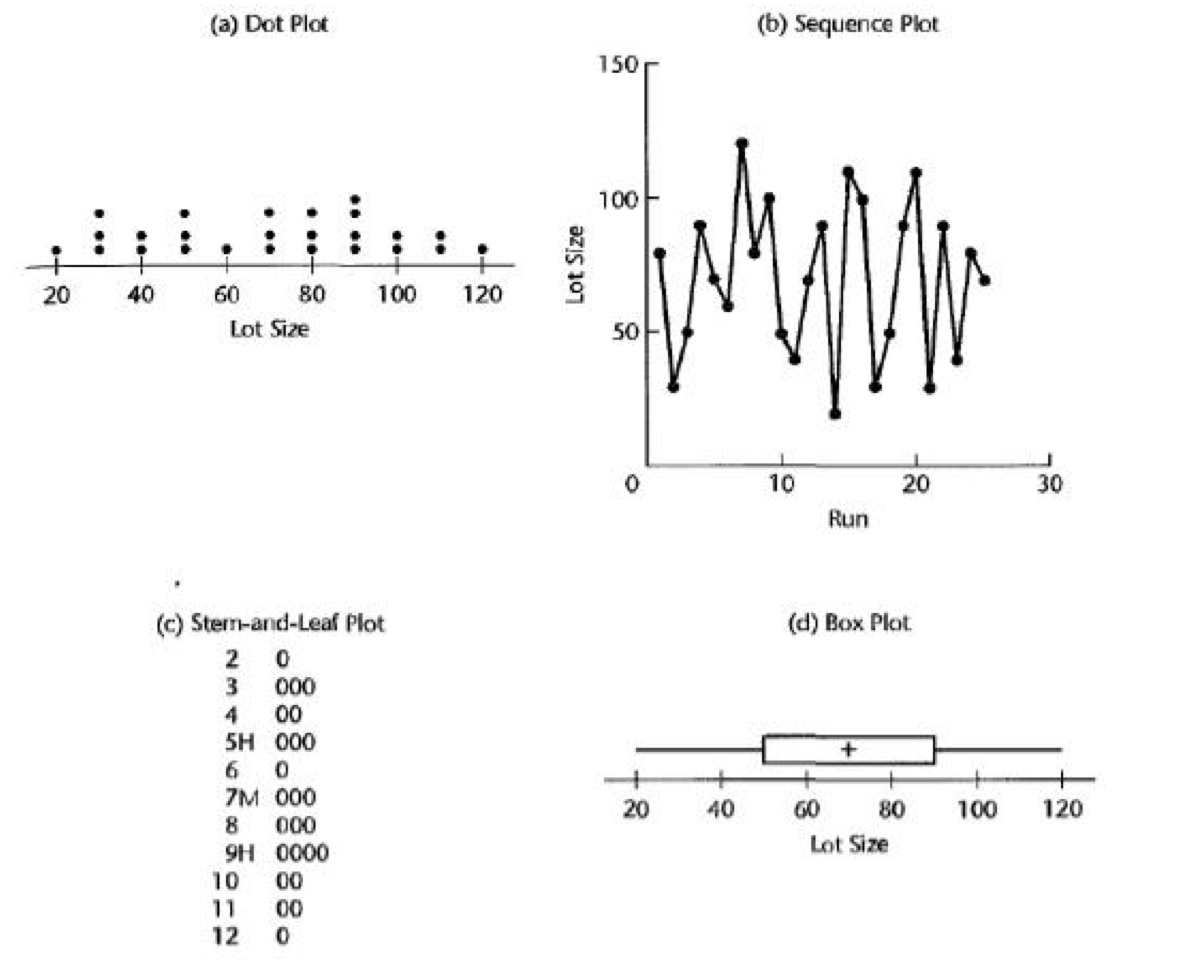
우리는 앞에서 linear model을 가정했다. 그렇다면 그 다음에는 이 모델이 적절한지, 우리의 가정이 잘 맞는지 확인하는 과정이 필요하다. 확인하는 방법으로는 주로 Graphical인 방법과 Statistical test 방법이 있다. 이 부분은 특히 Residu

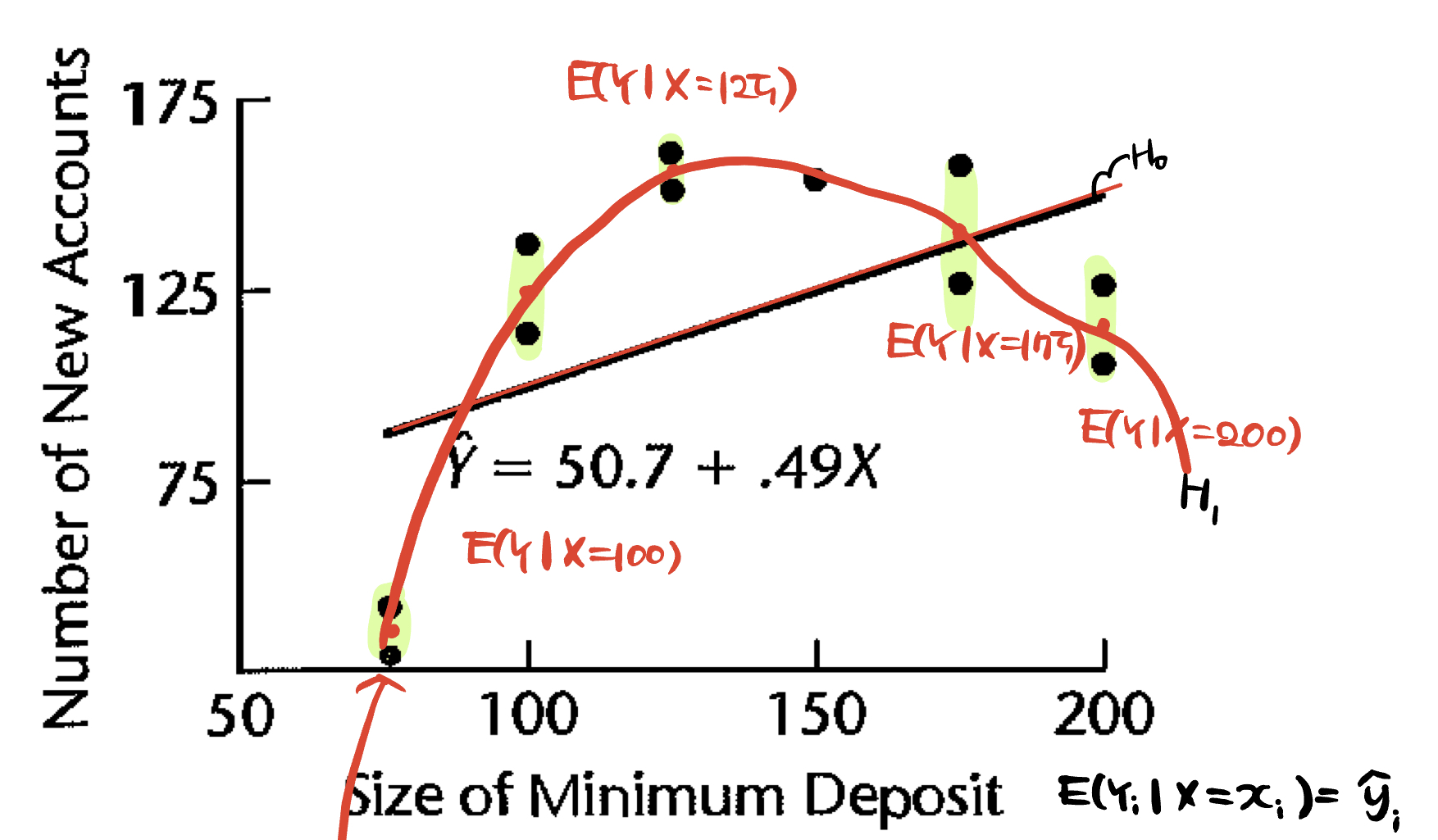
BP test는 BF test에서 잡아낼 수 없는 것을 잡아준다.예를 들자면, BF에서는 2개의 그룹으로 나누어 등분산성을 검정했다. 하지만 2개의 그룹의 variability는 같으나 각각의 그룹에서 또 그룹을 나눠서 생각해보면 등분산성이 깨질 수 있다. 그래서 그

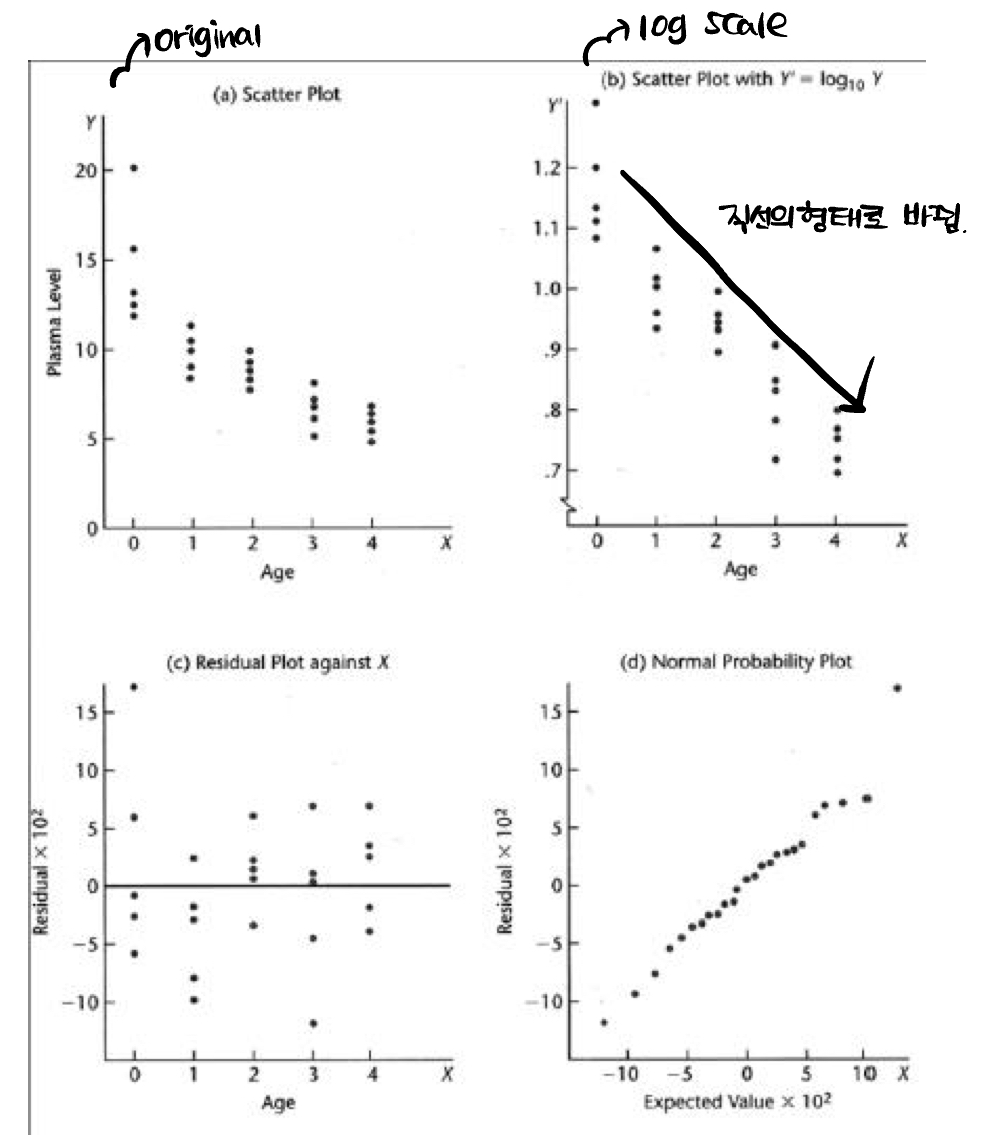
이전 포스트를 참고하면, $X$를 transform하는 상황과 $Y$를 transform 하는 상황까지 작성을 했다!방법은 다양하다.$logY$$\\sqrt{Y}$${1 \\over Y}$와 같이 transformation을 시도해보는 것이다.이것이 그 예시다.

최근에 너무 바빠서 글을 잘 작성하지 못했다... 지금도 사실 할 일이 계속 있는데... 그래도 이번주에 너무 포스팅을 하지 않아서 조금씩 해보려고 한다!: 원소를 직사각형 모양을 행과 열로 나열한 것요렇게 표현이 가능하다. matrix에서 행과 열을 바꾸는 것.다음과