Likelihood

likelihood는 한국말로는 우도라고 한다. (제주도 우도 땅콩 막걸리 맛있음) 조금 더 풀어서 설명하자면, 우리가 직접 관측한 데이터가 우리에게 주는 값이라고 생각하면 된다.

예시
10번 동전을 던졌고, 8번의 head가 나왔다면 이러한 정보에 근거해서 우리는 head가 나올 확률을 0.8이라고 말하는 것이 likelihood 이다.

Maximum likelihood estimation

(2)번 글에서도 작성해두었듯이, 관측값 $Y_i$의 regression model에서 error는 정규분포를 따른다고 했고 그에 따라 $E(Y_i) = \mathit{\beta}_0+\mathit{\beta}_1X_i$ 이고 $Var(Y_i) = \mathit{\sigma}^2$ 로 표현할 수 있었다.
그렇다면 Pdf(probability density function)을 다음과 같이 쓸 수 있다.

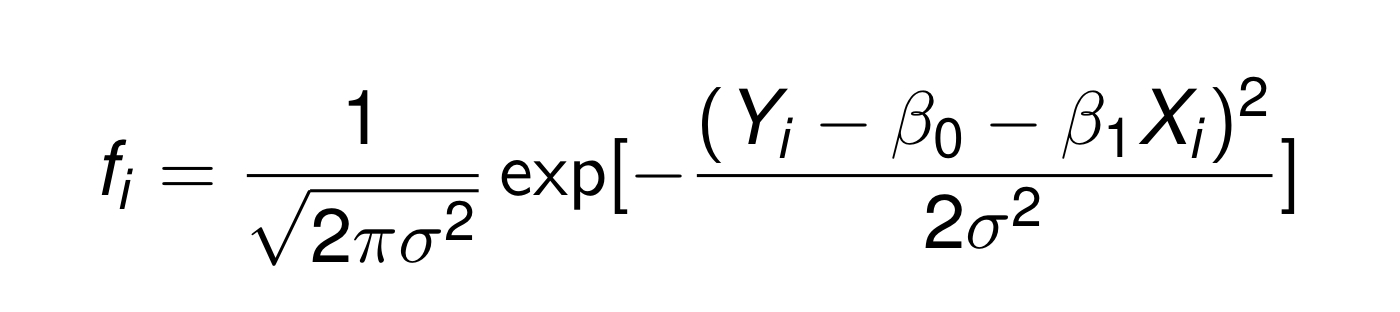
그러면 우리는 $Y_i$들을 각각 product한 것을 Likelihood function이라고 할 수 있다.
우리는 분산인 $\mathit{\sigma}^2$을 알지 못하기 때문에, Likelihood function은 사실 3가지의 모수를 추정해야하는 것이다. 바로 이 세가지 !! $\mathit{\beta}_0, \mathit{\beta}_1, \mathit{\sigma}^2$

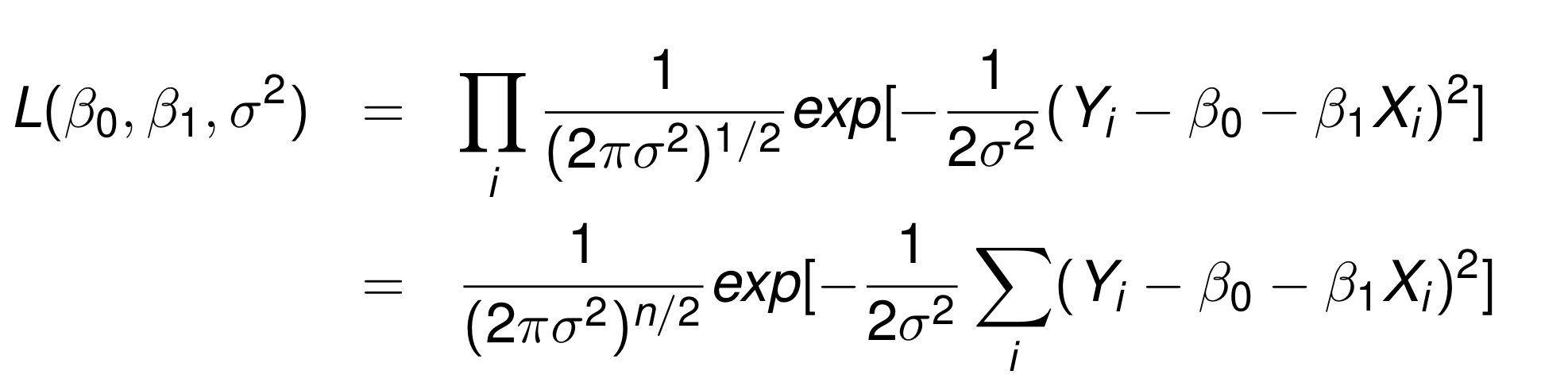
우리는 L이 최대화 되는 모수를 찾을 필요가 있기 때문에 각 변수에 대하여 편미분해서 0이 되는 값을 찾으면 된다.
이 과정에서 있는 그대로를 미분하지 않고, $logL$ 형태로 만들어 이용하는데, 그 이유는 $L$과 $logL$의 모수들이 만들어내는 최대치는 같기 때문이다.

복잡한 계산을 하시면 이런 결과를 얻을 수 있다.

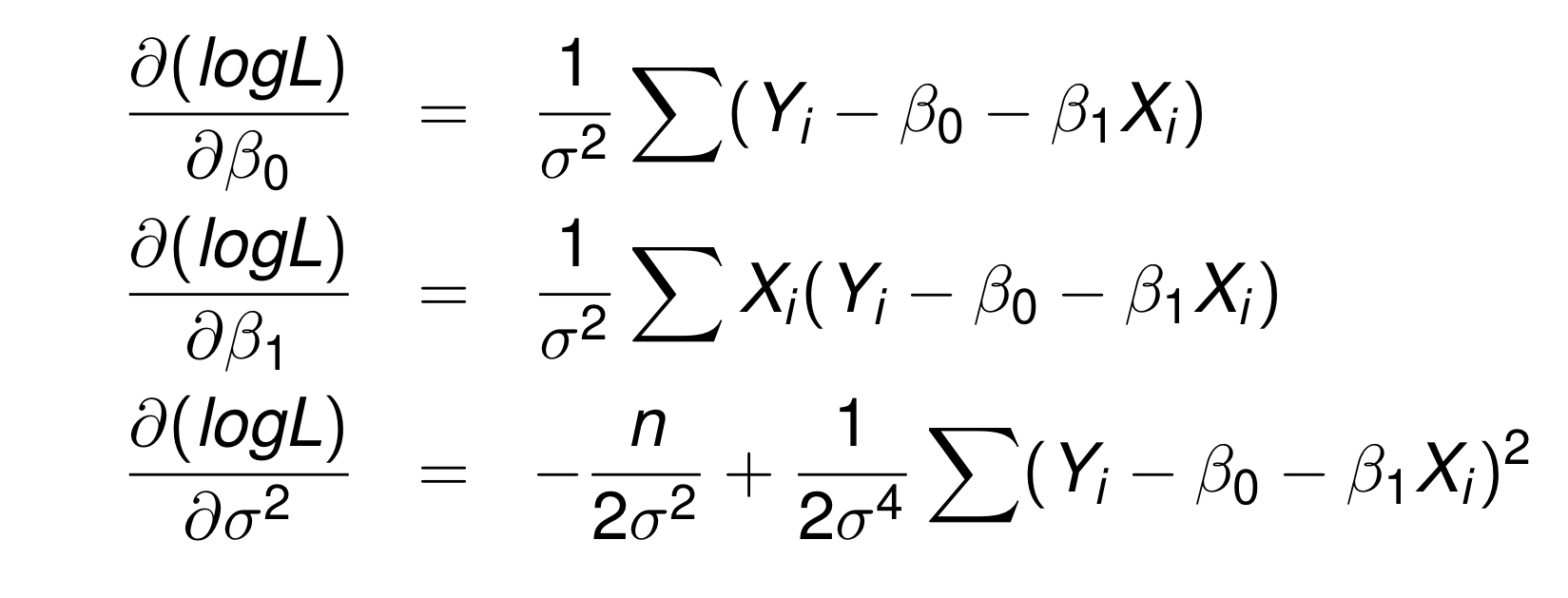
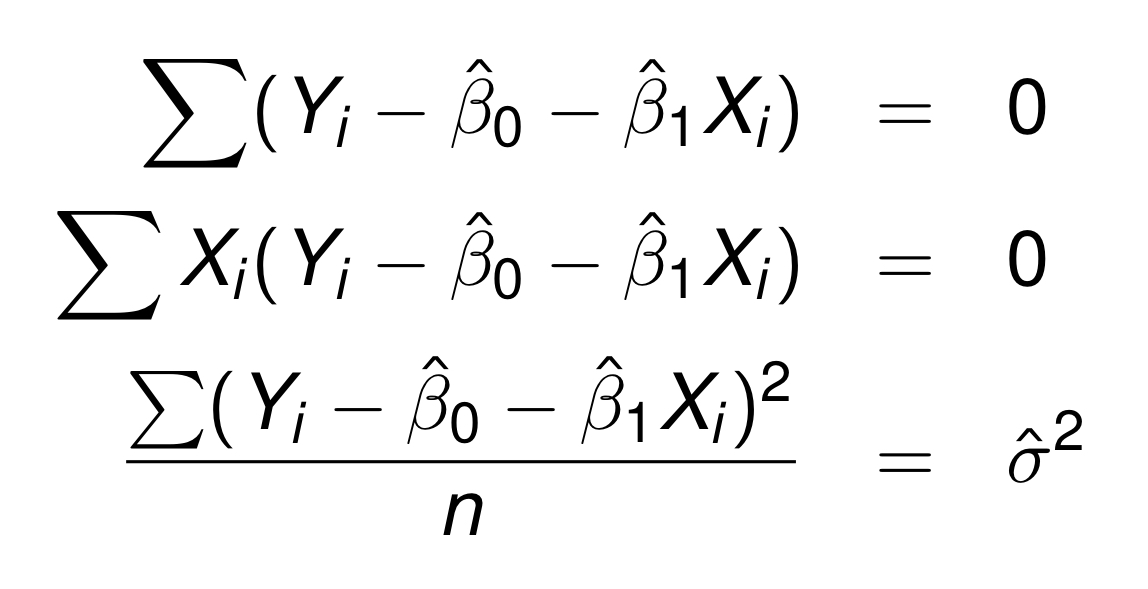
이제 이 Maximum likelihood estimation 결과와 Least Square에서의 결과를 비교해보자!

MLE vs LSE

MLE와 LSE에서의 회귀 계수 추정값은 동일하다. 하지만 주목해야할 점이 있다면, $\mathit{\sigma}^2$의 추정값이 다르다는 것이다. 다음 표를 참고해보자.

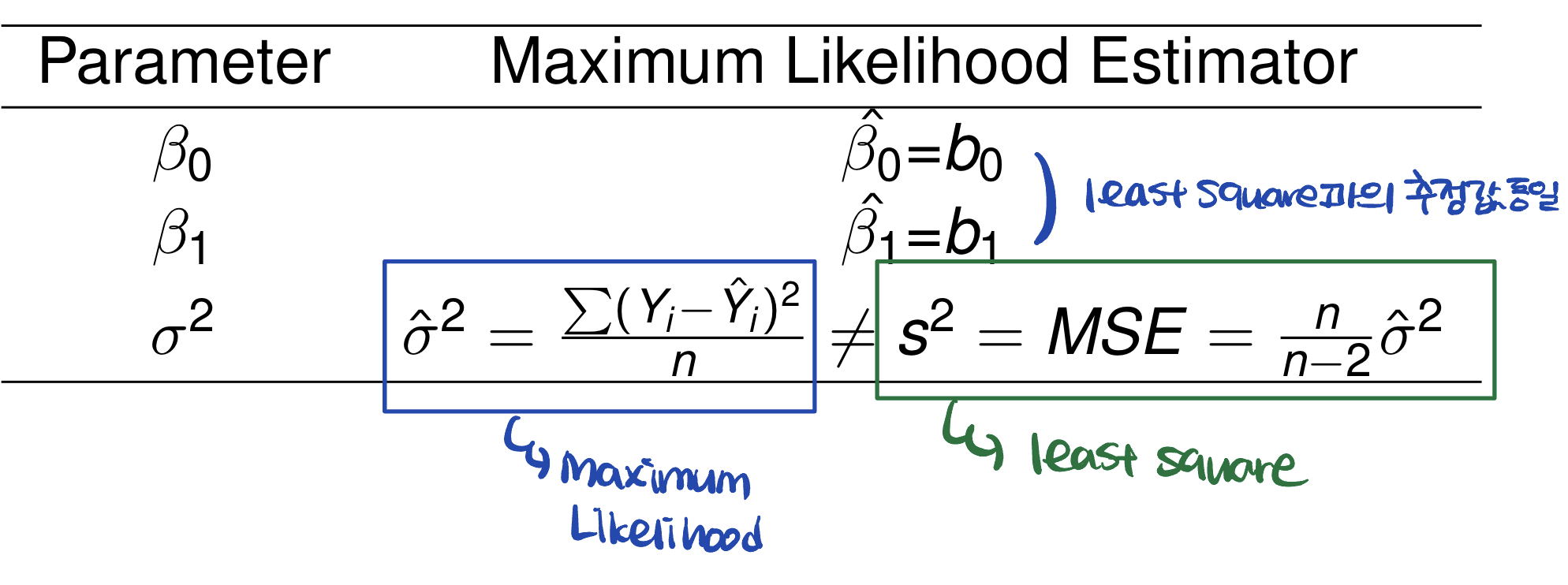
벨로그에는 표를 만드는 기능이 없나보다.. 티스토리보다 작성은 편한데 기능면에선 살짝 simple한 것 같아 아쉽다

여기까지가 변수가 1개일때의 linear Regression 내용이다. 내일부터는 testing에 대해서 다룰 예정이다!