$\hat{Y}_h$ estimation

(1) 번 포스트에서는 회귀계수의 추정값에 대해서 다루었다.
그렇다면 $\hat{Y}_h$의 estimation에 대해 알아보자.

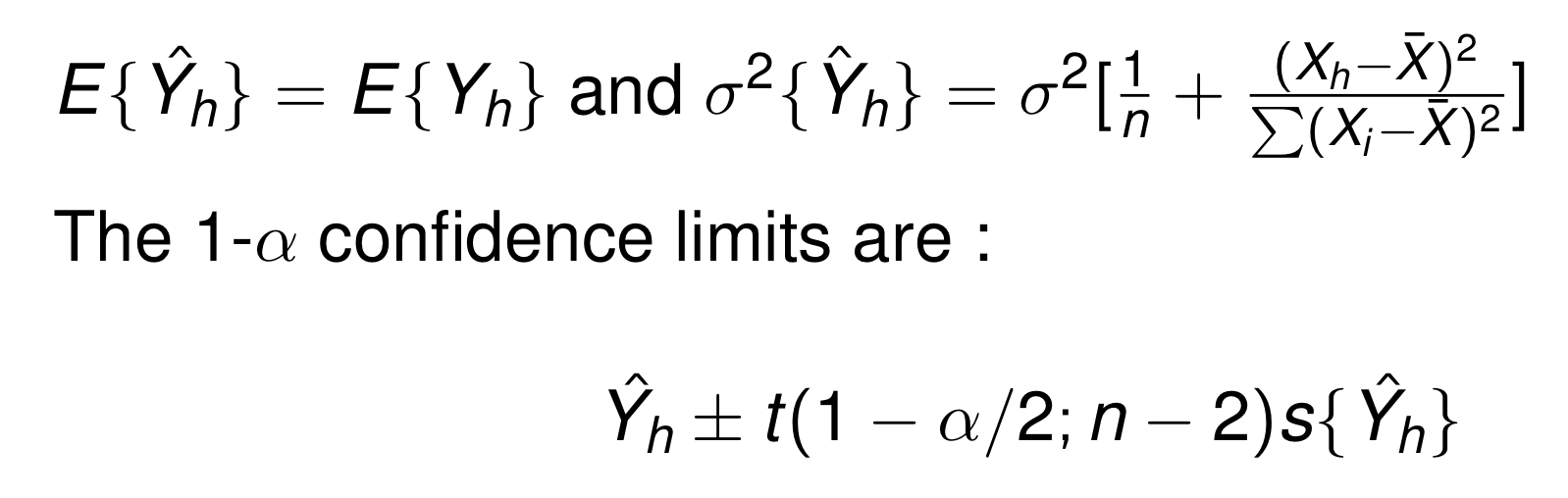
절대 TeX문법 쓰기 귀찮아서 이미지로 자꾸 첨부하는 것 아니다.
기댓값에 대해서는 기존의 선형 회귀 식을 생각해서, 그 자체에 기댓값을 씌운 것을 생각해보면 되기 때문에 어렵지 않게 이해할 수 있다.
분산의 경우 증명을 따로 다루지 않았다.

또.. 용어 정리

사실 내가 회귀분석을 공부하면서 가장 헷갈렸던 것이 줄임말들이었는데... 심지어 방 책상앞에 아직도 줄임말을 정리해둔 포스트잇이 붙어있다.

다시 정리해보자면,

SSTO : sum of square total
SSE : sum of square error
SSR : sum of square Regression
여기서 SSTO는 SSE와 SSR을 합한 것

나름 주의해야할 점으로는 SSE와 SSR을 헷갈리지 않아야 한다는 것인데, SSR은 말그대로 추정값에서 평균값을 빼준 것이고 SSE는 residual을 의미하는 것이다.

SSTO 쪼개보기

SSTO를 다음과 같이 쪼개볼 수 있다. 이렇게 쪼개는 skill은 통계를 공부하다보면 여러번 마주칠 수 있으니 너무 이상하게 받아들이지 말자~!

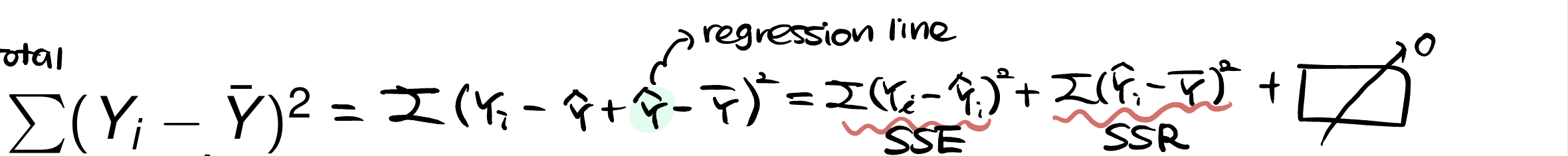
분해를 하면 SSE와 SSR의 합이 표현되어지고 , 외의 term은 0이 되어 사라진다. 이를 통해 SSTO가 일정하다면 SSE가 커질때 SSR은 작아지고, SSE가 작아지면 SSR은 커진다는 것을 알 수 있다!

ANOVA Table 분석하기

사실 지난 포스트에 R로 anova table을 출력해내는 것을 포스팅했었다. 더 자세하게 정리해두고 싶어 다시 정리한다.

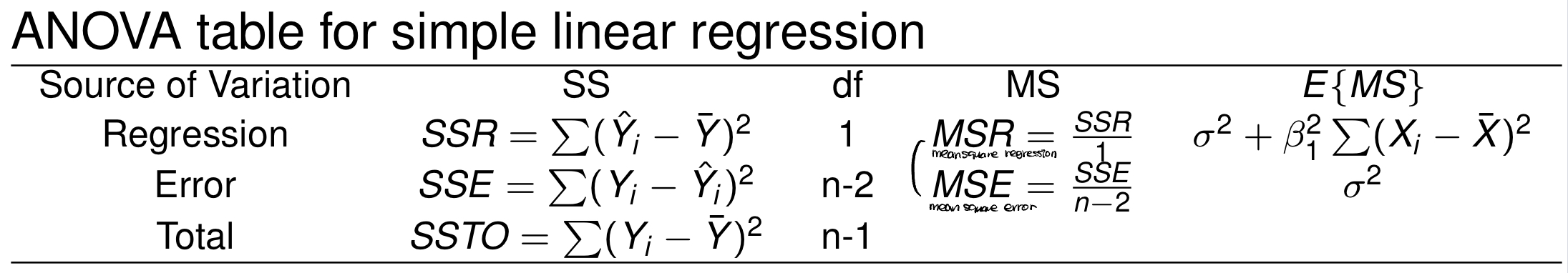
위에서 설명했던 SSR, SSE, SSTO값이 모두 나와있다. 그리고 다른 정보들도 나와있는데, df는 자유도, MS는 Mean Square 즉 SS를 각각의 자유도로 나누어준 값이다.

여기서 F-test를 시행해볼 수 있다. F test 검정통계량 값은 ${MSR \over MSE}$ 이다. 이에 따라 귀무가설 ($\mathit{\beta}_1 = 0$)을 기각하거나 채택할 수 있다.

여기서 중요한 것은 (1)번 포스트에 있었던 T-test의 결과와 F-test의 결과가 동일하다는 것이다. 참고로 T-test는 양측검정, F-test는 단측검정으로 진행하면 된다~! R에서는 qt와 qf함수를 적당히 잘 이용하면 된다!

General Linear Test

general linear test, (이하 GLT)에서는 full model과 reduced model이 무엇인지 잘 구분할 수 있으면 된다.

1. reduced model, 귀무가설 ($H_0$)
   $H_0$ : $\mathit{\beta}_0$
2. full model , 대립가설
   $H_1$ : $\mathit{\beta}_0+\mathit{\beta}_1X_i+\mathit{\epsilon}_i$

이렇게 두가지의 가설을 세울 수 있다. 즉 $\mathit{\beta}_1$이 0인지 0이 아닌지에 대한 싸움임을 알 수 있다.
GLT같은 경우는 앞으로 계속 나오므로 잘 정리해두는 것이 좋은 것 같다.

먼저 full model의 SSE를 구해보면 우리가 아는 형태의 SSE와 동일하다.
$SSE(F) =\sum(Y_i-(b_0+b_1X_i))^2=\sum(Y_i-\hat{Y}_i)^2$

reduced model의 SSE 역시 구해보면
$SSE(R) = \sum(Y_i-b_0)^2 = \sum(Y_i-\bar{Y})^2=SSTO$
와 같이 결과를 얻을 수 있다.

이를 통해 F-test 검정통계량을 구해보자.

$F^* = {{SSE(R) - SSE(F)} \over {df_R - df_F}} / {SSE(F) \over df_F} = {{SSTO -SSE} \over {(n-1)-(n-2)}} / {SSE \over n-2} = {MSR \over MSE}$

GLT에서의 $F^*$는 위의 anova table에서의 F검정 통계량과 동일하다는 것! (단 이것은 simple linear regression에서만 동일하다.)

그리고 추가로 내가 구한 SSE의 값이 작다면 나의 Regression 이 꽤 잘맞는다고 판단하면 된다. 만약 반대로 나의 SSR이 작다면, 거의 안맞는 추정이라고 판단하면 될 것이다.

Coefficient of determination, R square

R-square는 다중회귀부분에 들어가면 판단의 값으로 다시 등장하게 된다.
우선 R-square의 정의는 다음과 같다.

$R^2 = {SSR \over SSTO} = 1-{SSE \over SSTO}$
단 $R^2$의 값은 0과 1사이에만 존재한다는 것.

해석을 해보자면
1. $R^2 = 1$ : 나의 SSE가 0이다. 즉 나의 회귀 값이 완전히 perfect하다.
2. $R^2 = 0$ : 나의 SSR이 0이다. 즉 SSE가 크다는 의미이고 나의 추정이 완전히 틀려먹었다.

$R^2$의 값은 클수록 좋다는 것을 반드시 기억해두자. 후에 다중회귀에서 다시 등장한다!

---

to be continued