들어가기전에...

우리는 앞에서 linear model을 가정했다. 그렇다면 그 다음에는 이 모델이 적절한지, 우리의 가정이 잘 맞는지 확인하는 과정이 필요하다.
확인하는 방법으로는 주로 Graphical인 방법과 Statistical test 방법이 있다.
이 부분은 특히 Residual이 main인 부분이다!
왜냐면 residual은 random error에 대한 정보를 가지고 있기 때문이다.

Plots

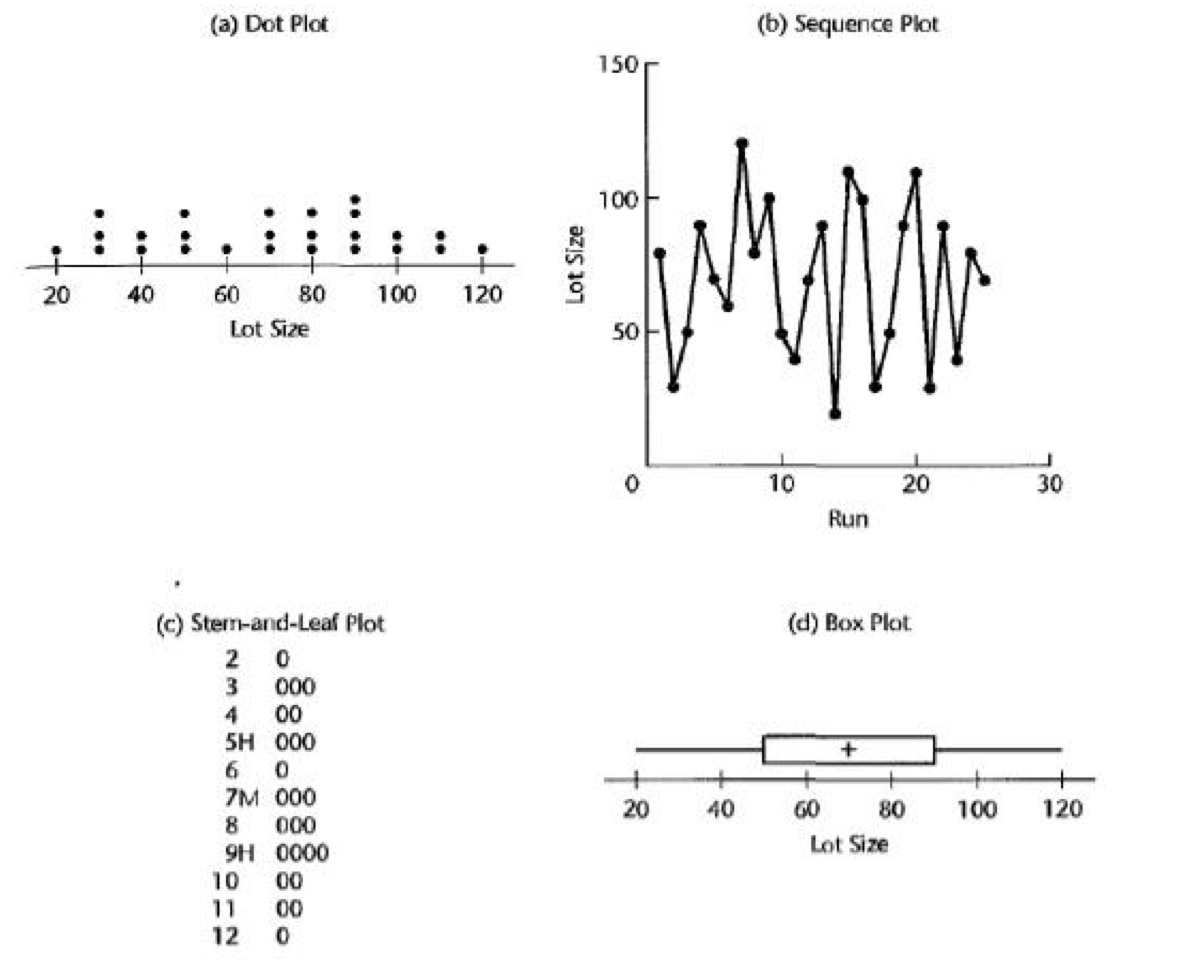
각 Plot들을 통해 쉽게 얻을 수 있는 정보가 있다.
1. Dot plot은 최대, 최솟값, outlier, 케이스의 수를 파악할 수 있다.
2. Sequence plot은 시간의 흐름을 나타낸다.
3. 줄기와 잎 plot은 정규성과 빈번도, 범위, quantile을 알 수 있다.
4. Boxplot은 분포, 범위, 중간값, 평균, outlier, quantile을 알 수 있다.

Residual과 Random error는 썸타는 사이

random error, 즉 알려지지 않은 진짜 error는 다음과 같이 표현한다.

반면 Residual은 우리가 직접 관측한 error이며 다음과 같이 표현한다.

Residual과 Random error는 썸타는 사이이다. 왜냐하면 residual에는 random error에 대한 정보가 있기 때문이다. 내안에 너있다

여기서 Residual의 mean과 variance를 구해보면

mean : $\bar{e} = {\sum{e_i} \over n} = 0$
Variance : $s^2 = {\sum{(e_i-\bar{e})^2} \over n-2} = {\sum{e_i^2} \over n-2} = {SSE \over n-2} = MSE$

위와 같이 표현된다. 여기서 $e_1, e_2, ... e_n$은 independent하지 않다.
우리가 Residual을 통해 판단해야할 것들은 다음과 같다.

1. Regression function is not linear
2. errors have not constant variance
3. a few observations are outliers
4. errors are not independent
5. errors are not normal.

Diagnostics for Residuals

Residual plot에서는 수직축이 residual을 의미하게 되고, 수평축은 Fitted value를 의미하게 될 것이다.

Case 1. Regresiion function is NOT Linear.

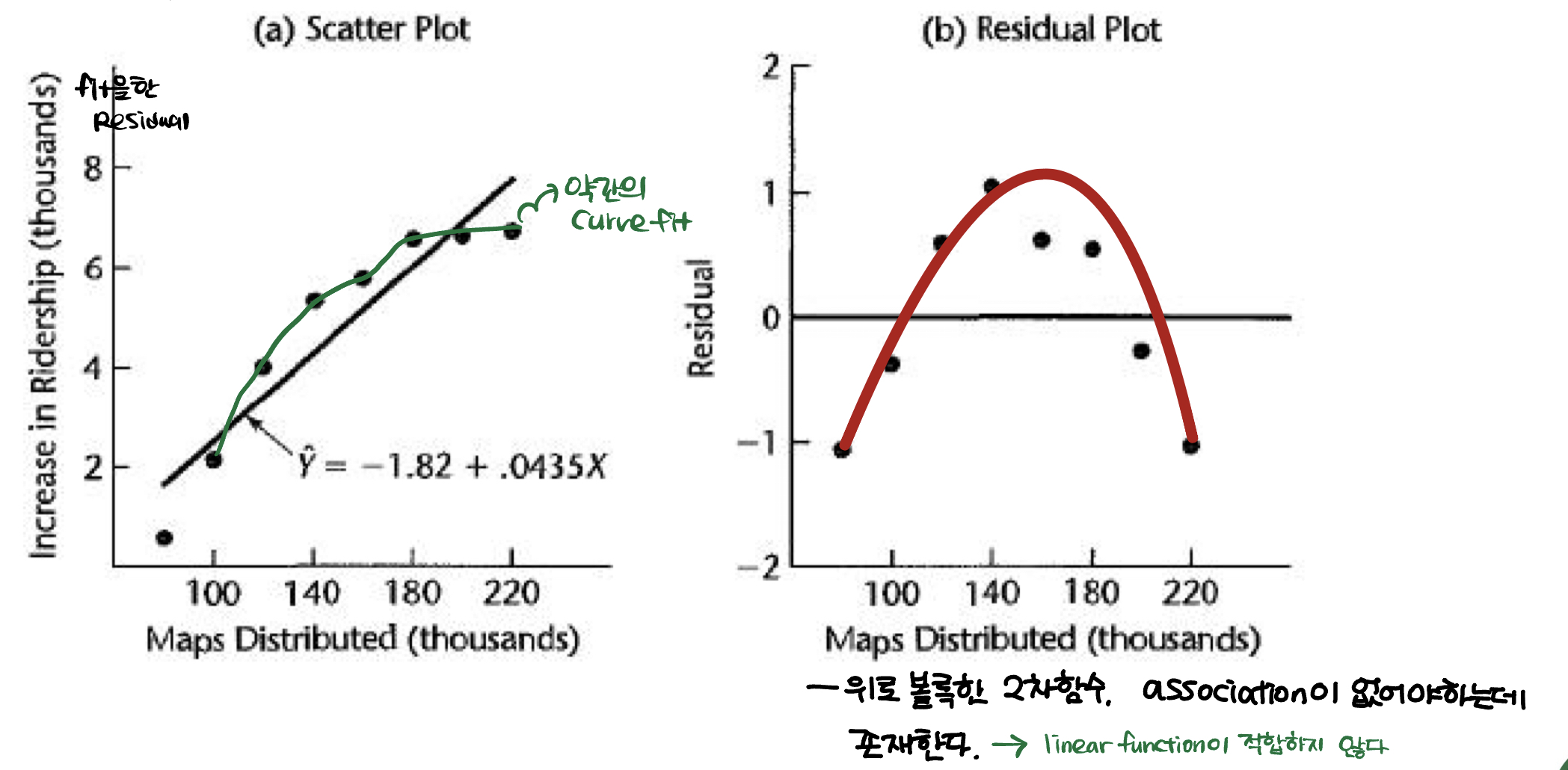
다음 그림을 보자!
scatter plot에서는 약간의 curve가 있긴 하지만 regression이 나빠보이지 않는다. 하지만 residual plot에서 위로 볼록한 이차함수꼴이 보인다. association이 존재해서는 안되므로, 우리의 regression이 적합하지 않다는 것을 파악해야한다.

Case 2. Errors have Not constant variance. (등분산성이 깨짐)

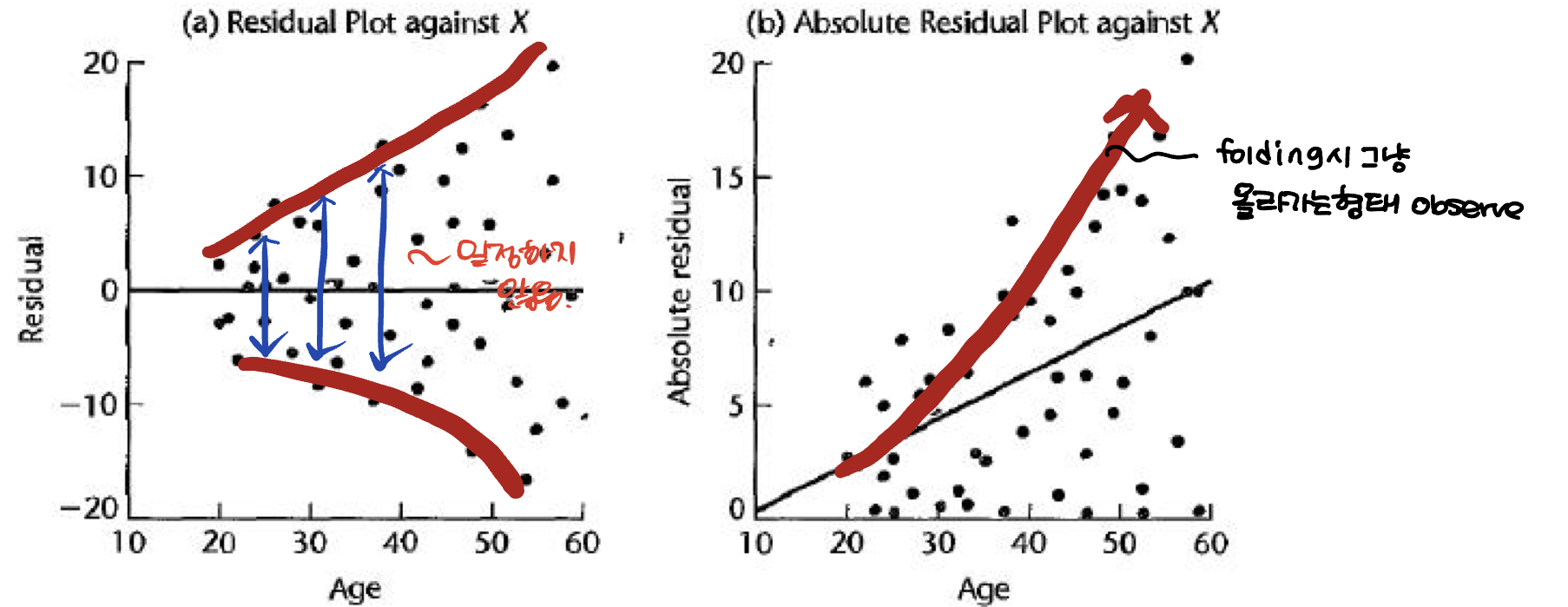
(a)번 Plot을 보자. $x$가 커짐에 따라 residual의 분산이 커진다. 사실 음수쪽에도 dot이 찍혀있으므로, 우리는 이를 fold (절댓값) 해서 확인해볼 수 있다. 절댓값으로 확인해보면 residual이 계속 올라가는 형태가 관측된다. 이것은 등분산성을 만족하지 못한다는 의미이다!

Case 3. outliers

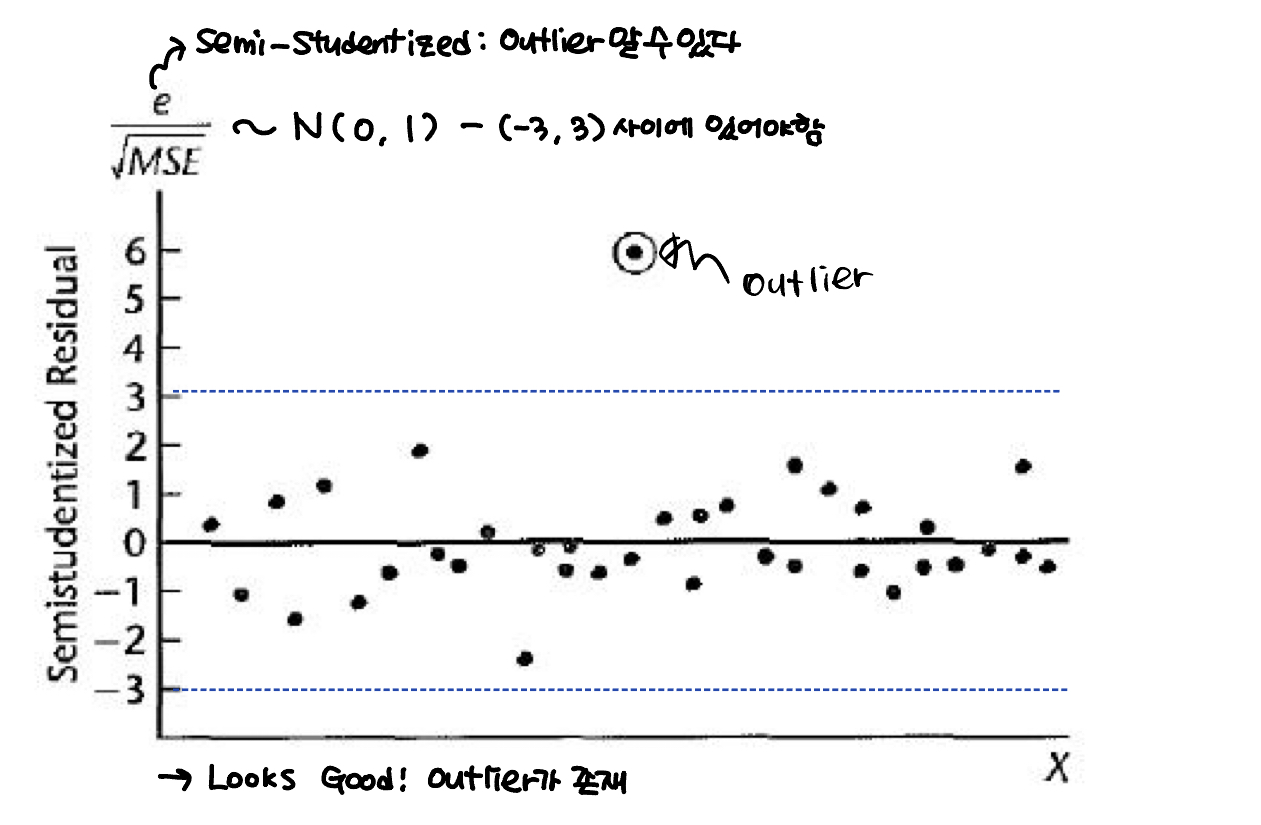
Semi - Studentized residual은 $e \over \sqrt{MSE}$ 이고, 이것은 residual을 정규화한 것이다. semi-studentized residual을 이용하면 outlier 파악에 용이하다.
위의 plot을 보자!
(-3,3) 범위에서 벗어난 outlier가 하나 존재한다.
꽤나 괜찮아보인다고 판단할 수 있다.

Case 4. Errors are not independent

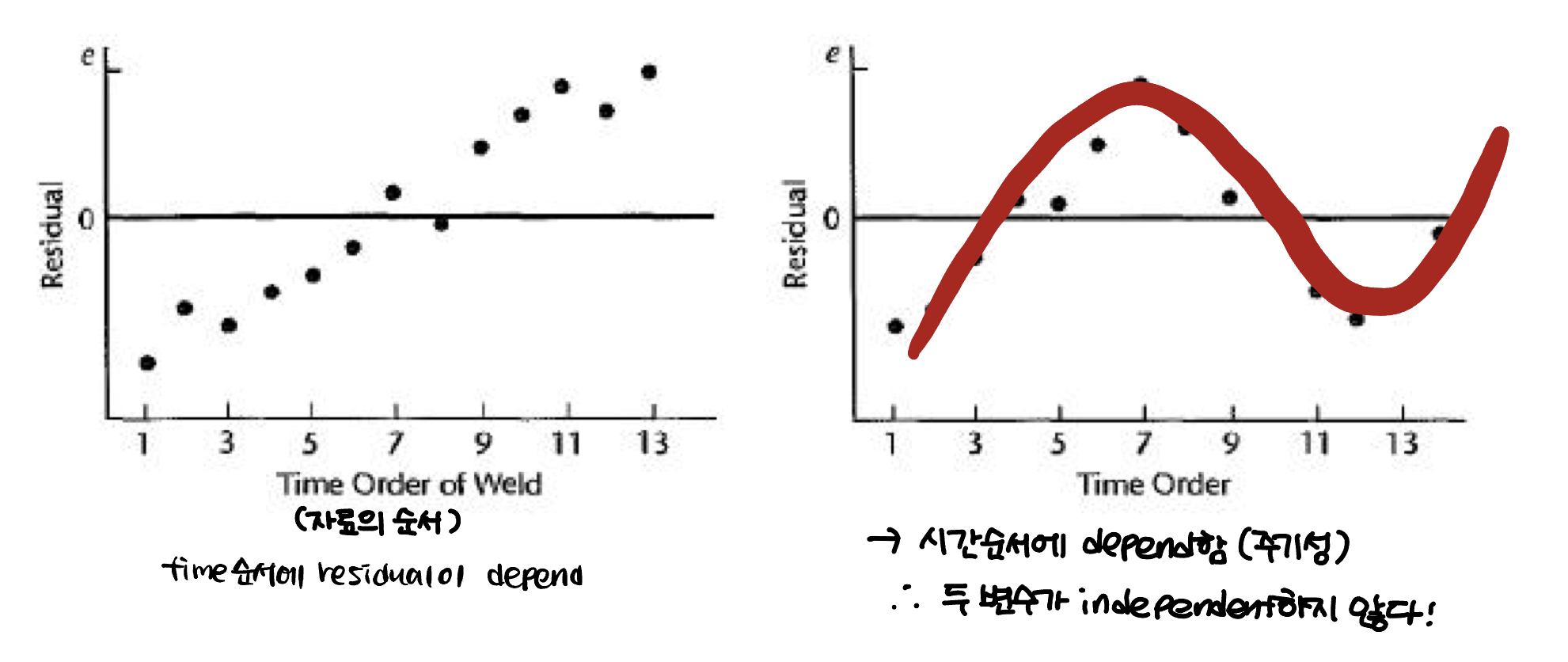
두개의 sequence plot을 보자.
첫번째는 시간에 따라 residual이 커지는 것을 볼 수 있다. 두 변수가 dependent하다는 것을 알 수 있다.
두번째 그림도 마찬가지이다. 시간에 따른 주기성을 갖는다고 볼 수 있으므로 두 변수가 독립이 아니라는 것을 알 수 있다.

Case 5. Errors are not Normal

QQ-plot에서 residual이 정규분포 $N(0, MSE)$ 를 따른다면 plot이 직선형태로 그려져야한다.(order를 생각해보면 된다!)

물론 가장 이상적인 형태는 직선의 모양이지만 다음과 같은 형태를 띨 수 있다.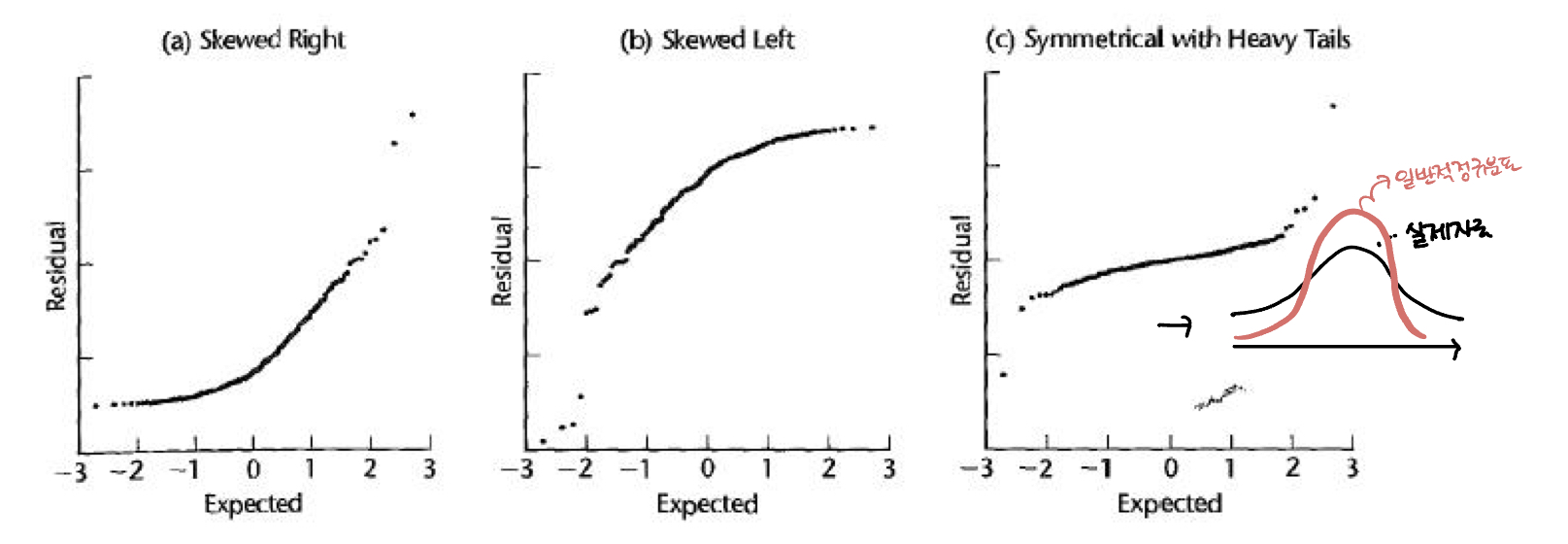

특히 (c)같은 경우에는 실제 자료 분포가 일반적인 정규분포보다 훨씬 경사가 완만한 모양을 띈다.

Tests For Homogenious Variance

How to Brown - Forsythe Test? (BF test)

BF test는 다음과 같은 순서로 진행한다.
1. linear regression을 진행하고, residual을 얻는다.
2. residual data를 두개의 그룹으로 나누어준다.
3. $e_{1i}, e_{2i}$를 두 그룹의 $i$th residual이라고 해보자.
4. $d_{1i} = \left\vert e_{1i} - \tilde{e}_1 \right\vert, d_{2i} = \left\vert e_{2i} - \tilde{e}_2 \right\vert$ 라 하자. 여기서 $\tilde{e}$는 각 그룹에서의 median이고, $d$는 거리를 의미한다.
5. 등분산성에 대한 sample t-test를 진행한다.

BF test는 아주 신뢰성이 있고 검정결과가 좋다고 한다.
귀무가설과 대립가설은 다음과 같이 세우면 된다!

$H_0$ : constant variance
$H_1$ : not constant variance

검정통계량은 $d_{1i}=d_{2i}$ 일때의 t-test로 진행하면 된다.
두 집단의 variablity가 같다는 의미는 $d_{1i}$의 sample mean=$d_{2i}$의 sample mean이라는 의미.

내가 궁금했던 것

보통 median보다는 평균을 많이 사용한다고 생각했고, 당연히 여기서도 평균을 사용해야한다고 생각했는데, median을 사용해야 outlier에 덜 민감해진다고 한다.

---

to be continued