Intro.

럭키백으로 대박 친 한빛마켓! 이젠 패션 시장까지 진출하기로 하고, 이번에도 럭키백 이벤트를 진행하기로 결정! (생선 럭키백은 무게, 길이 등의 정형 데이터로 했다면, 이번에 패션 럭키백은 이미지 픽셀을 사용할 거임.)
홍 선배🗣️ "생선 럭키백에 썼던 로지스틱 회귀 알고리즘보다 정확도를 높일 순 없을까..."

1. 패션 MNIST 데이터셋

• 딥러닝의 고전적인 예제 데이터셋으로, 딥러닝 라이브러리 내에 기본 내장되어 있음!
• 'MNIST' 데이터는 원래 손으로 쓴 0~9의 이미지인데, 이건 '패션 MNIST'라서
  10종류의 패션 아이템(이미지)으로 구성되어있음.

데이터 가져오기

• keras의 .load_data()함수는 훈련/테스트 세트 나눠서 데이터를 불러와 줌.
  
• 크기를 확인해보니,
  훈련세트 : 입력은 28x28픽셀 이미지 60,000개 / 타깃은 0~9의 숫자 60,000개
  테스트세트 : 훈련세트와 동일한 조건의 이미지 10,000개 / 상응하는 타깃도 마찬가지
  

데이터 그려보기

• 그림으로 확인해보니, 다양한 종류의 패션 아이템이 그려짐.
  + 타깃을 확인해보니, 같은 종류의 아이템끼리 같은 숫자에 할당되어 있음.
  
• 참고로, 패션MNIST에 포함된 10개의 레이블은 아래와 같음. (*그림 출처)
  
• np.unique()로 레이블마다 몇 개씩 들어있는지도 확인해 봄.
  

2. 로지스틱 회귀로 만든 럭키백

모델 선택 & 데이터 전처리

• 훈련 샘플이 60,000개나 되기 때문에 한 번에 다 사용하는 것보다 하나씩 꺼내서 훈련하는 것이 더 효율적일 듯 → 손실함수를 로지스틱으로 한 SGD 쓰자!
• SGDClassifier는 표준화 전처리 필요했었음 → 근데 어차피 각 픽셀들이 0~255 사이의 정수니까, 그냥 255로 나눠서 정규화하곤 함! (이미지 전처리 시 널리 쓰는 일종의 관례)
  

모델 훈련

• 경사하강법을 활용한 로지스틱 회귀모델을, cross_validate로 훈련 & 평가함.
  
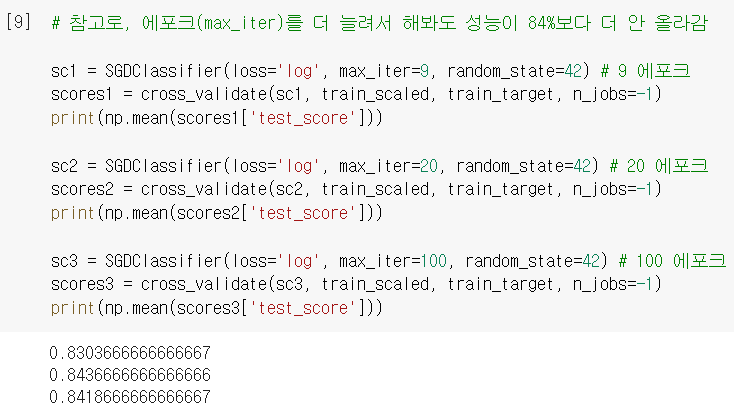
• 에포크 더 늘려서 해봐도 성능이 썩 만족스럽지는 않음 ...
  (※ 까먹었을까봐 다시 얘기하는데, 'test_score'는 테스트세트의 점수가 아니고 검증세트의 점수!!)
  

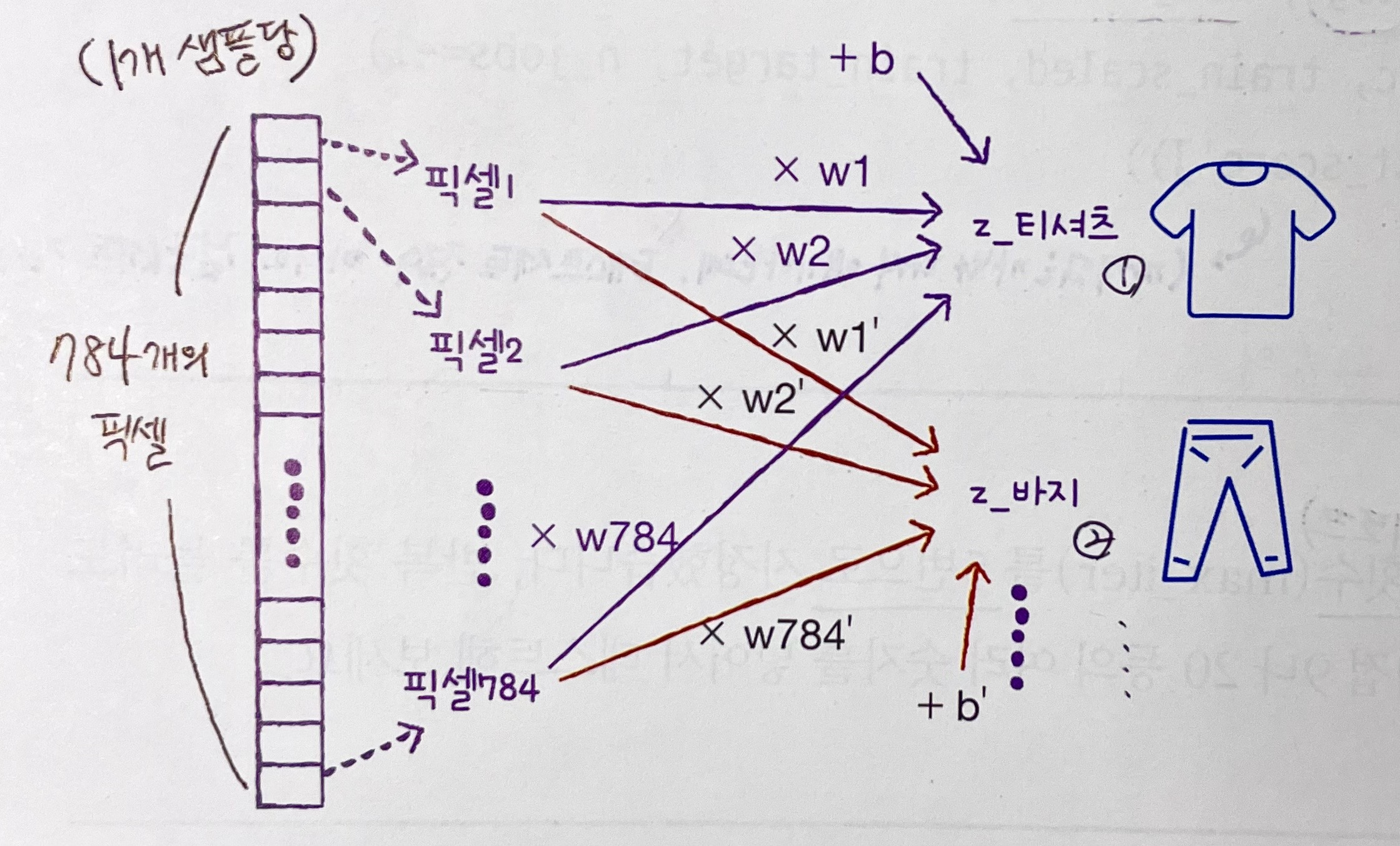
방정식 살펴보기

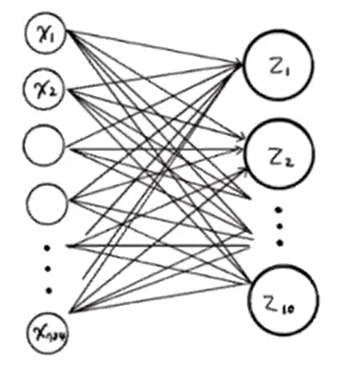
• 4장에서 배웠던 로지스틱 회귀 방정식을, 이 경우에 맞게 생각해보자. (복습 차원)

$z\_Tshirt = w1\times(픽셀1)+w2\times(픽셀2)+...+w784\times(픽셀784) +b$
$z\_Trouser = w1'\times(픽셀1)+w2'\times(픽셀2)+...+w784'\times(픽셀784) +b'$
$z\_Pullover = w1''\times(픽셀1)+w2''\times(픽셀2)+...+w784''\times(픽셀784) +b''$
$⋮$
이런 식으로 10종류 레이블에 대한 방정식 10개가 있는 거임! → 그리고 거기서 구한 $z$값 10개를 소프트맥스 함수에 넣으면 각 레이블에 대한 확률을 얻을 수 있는 것! = ✴️럭키백✴️

3. 인공 신경망

너는 이미 알고 있다?

조금 어이없게 들릴 수 있지만, 사실 우리는 이미 인공신경망을 만들었습니다..!
가장 기본적인 형태의 인공신경망은 SGD를 사용하는 로지스틱 회귀와 똑같거든요...^^

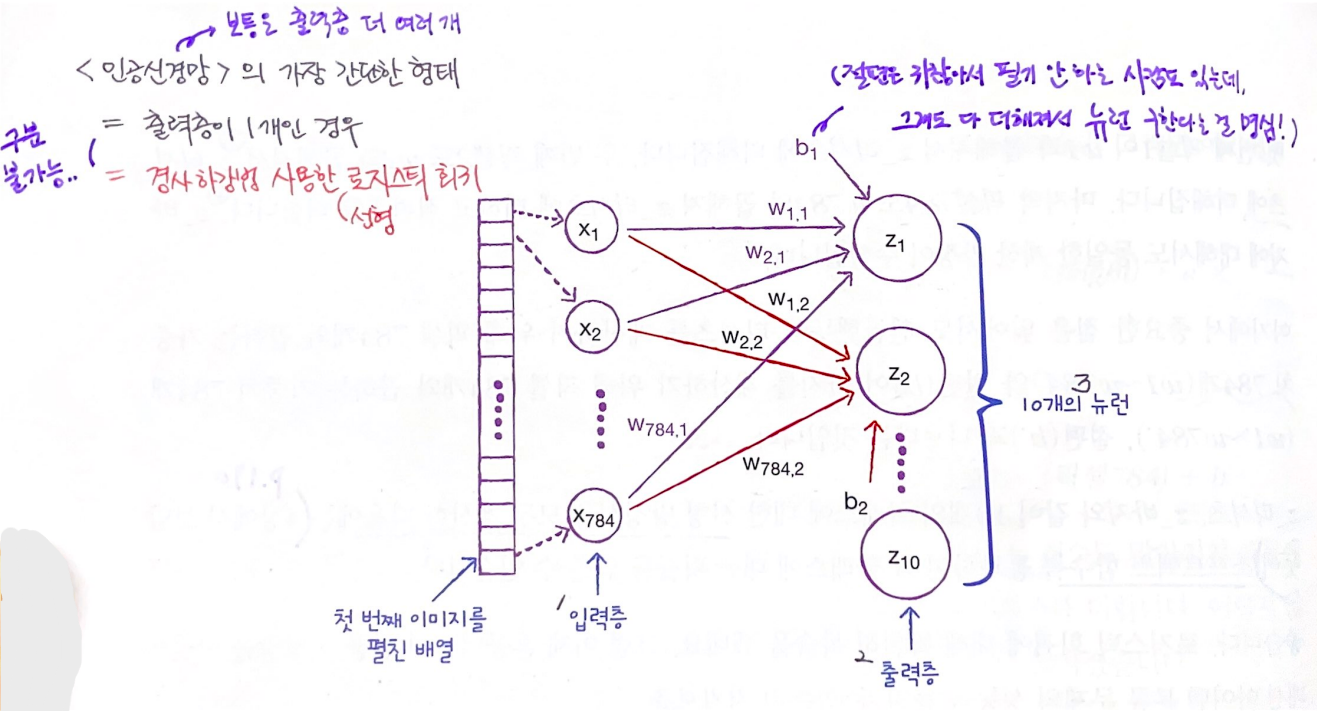
• 1) 픽셀1, 픽셀2, ... 였던 것을 x1, x2, ... 로 나타냄 = 입력층
  • 특별한 계산이 수행되지 않은, 그냥 '입력 데이터'로 보면 됨.
  • 그래서 '층'이라고 하기 애매하지만, 관례상 '입력층'이라고 부름.
• 2) z_Tshirt, z_Trouser, ... 였던 것을 z1, z2, ... 로 나타냄 = 출력층
  • 신경망의 최종 결과값을 만드는 층
  • 보통은 입력층과 출력층 사이에 더 많은 층이 있음.
• 3) z값을 계산하는 단위 = 뉴런 (요새는 유닛이라고 더 많이 부름)
  • 여기서 10개 유닛은, 로지스틱회귀의 선형방정식 10개와 동일한 느낌.

인공신경망의 유래

• Warren McCulloch와 Walter Pitts가 처음 제안한 것으로, 생물학적 뉴런에서 영감 받음.
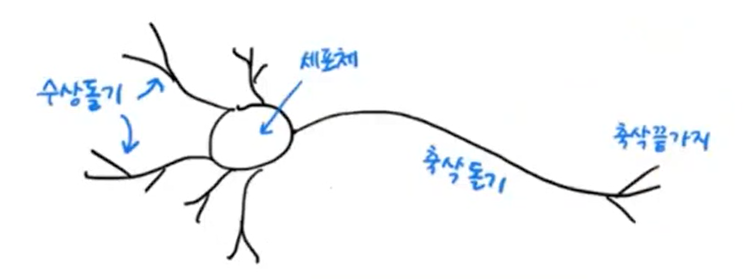
  • 수상돌기에서 신호 받아서 축삭돌기를 통해 다른 세포에 신호를 전달함.
    
• But, 생물학적 뉴런이 '가중치와 입력을 곱하여 출력을 만드는' 것은 아님!!
  • 그냥 모양만 본뜬 것이지, 실제 생물학적 뉴런과 동일한 게 절대 아님.
  • 기존의 것보다 더 높은 성능을 발휘하는, 새로운 종류의 머신러닝 알고리즘일 뿐.
    

딥러닝 라이브러리

• 다른 머신러닝 라이브러리와 달리, GPU를 사용해서 인공신경망을 훈련함.
  (벡터와 행렬 연산에 최적화되어있어 훨씬 빠르게 훈련 가능!)
  
• 텐서플로 : 구글이 오픈소스로 공개한 딥러닝 라이브러리.
  케라스 : 텐서플로의 고수준 API (텐서플로가 케라스의 백엔드)
  

인공신경망 모델 만들기

• 딥러닝에서는 교차검증을 잘 안 씀. → 검증세트를 직접 덜어내서 사용함.
  
• 케라스의 Dense() 클래스로 출력층 객체를 생성함.
• keras.layers : 다양한 층 클래스를 담고 있는 케라스 패키지 → 그 중에 가장 기본적인 '밀집층'(➕플러스알파 참조)을 사용해 본 거임.
• activation : 각 유닛에서 출력되는 z값들을 적용할 활성화함수 지정하는 매개변수
  (🆚만약 이진분류라면 activation='sigmoid'로 설정해야겠지 ㅇㅇ)
  input_shape : 입력값의 크기를 넣는 매개변수 (튜플로 지정해야 함!)
  
• Sequential() : 만들어둔 층 객체로 신경망 모델을 생성해주는 클래스
  (보통은 층 여러 개 만들어서 쌓는 건데, 지금은 dense 하나밖에 없어서 좀 뻘쭘...^^)
  
• 드디어 처음으로 신경망 모델을 만들었음! 그걸 간단한 그림으로 보면 아래와 같음.
  → 이제 이 model로 훈련시키면 되는 거임!
  

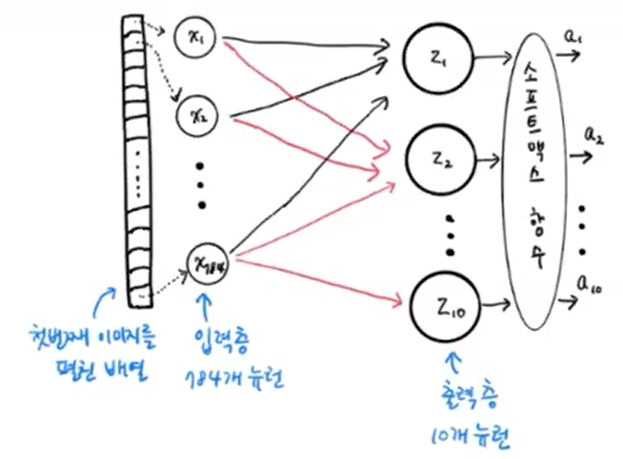
4. 인공신경망으로 만든 럭키백

설정 단계

• 지금까지 썼던 사이킷런과 달리, 케라스 모델은 훈련하기 전에 설정 단계가 따로 있음.
  ➡️ .compile() 에서 손실함수, 측정값 등을 설정하면 됨!
  
• loss : 손실함수의 종류 (이거는 필수!!!!⭐)
  - 이진분류는 loss='binary_crossentropy' ; 이진 크로스 엔트로피
  - 다중분류는 loss='categorical_crossentropy' ; 크로스 엔트로피
  - 근데, sparse_categorical_crossentropy❓
  원래 다중분류에서 크로스엔트로피 손실함수를 쓰려면 타깃값에 '원-핫 인코딩' 처리를 해줘야 함(➕플러스알파 참조). 근데, 그걸 안 하고 그냥 정수로 된 타깃값을 그냥 사용할 경우에 이 손실함수를 사용함.
• metrics : 기본적으로 출력되는 '손실 값' 이외에 추가로 측정하고 싶은 값.

훈련 단계

• 역시역시나 .fit()으로 하면 됨! + 반복할 epoch 횟수 지정
  
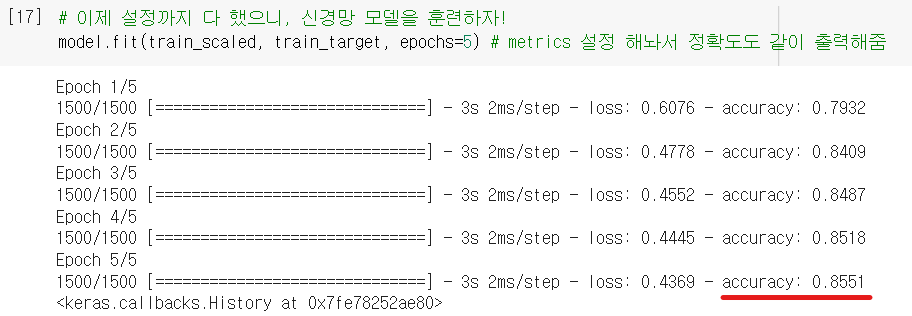
• 에포크마다 걸린 시간, 손실, 정확도를 출력해줬네. + 5에포크 밖에 안 했는데 이미 로지스틱 모델(p.345)보다 성능 좋아짐!😁

평가 단계

• 케라스에서는 .evaluate() 로 모델 성능 평가함. (🆚 사이킷런은 .score() 였음)
  → 떼어냈던 검증세트의 성능도 평가해 봄. (원래 훈련세트보다 조금 낮은 게 일반적)
  

드디어 처음으로 딥러닝(인공신경망)을 사용해서 패션 럭키백 분류 모델 완성!!

5. API 방식 비교

머신러닝 작업에서 썼던 Sklearn과, 이번에 딥러닝 작업으로 쓴 Keras의 사용방식을 비교해봄.

사이킷런 모델

• 모델 객체 만들면서 웬만한 매개변수 다 지정함 ➡️ fit으로 훈련 ➡️ score로 평가
  

케라스 모델

• 사이킷런보다 모델 만드는 과정이 더 세분화된 느낌..! (훈련&평가 과정은 비슷)
  ↪ 이러면 보다 다양한 조합의 모델을 창조할 수 있겠죠!
• 층 객체를 따로 만들고 ➡️ 그걸 모델에 Sequential로 추가하고 ➡️ 그 모델의 설정도 compile로 따로 해줌 ➡️ fit으로 훈련하는 건 똑같고 ➡️ 평가는 evaluate로 함
  

➕플러스 알파

➊ 밀집층 (Dense layer)

• 모든 입력과 모든 유닛을 선으로 이어보면 빽빽하게 들어차서 그렇게 부름.
• 입력층과 출력층이 하나하나 다 연결되어 있어서 '완전연결층(fully connected layer)이라고도 부름.
  

➋ 원-핫 인코딩⭐

<'categorical_crossentropy' 앞에 붙은 'sparse'는 무엇인가?>

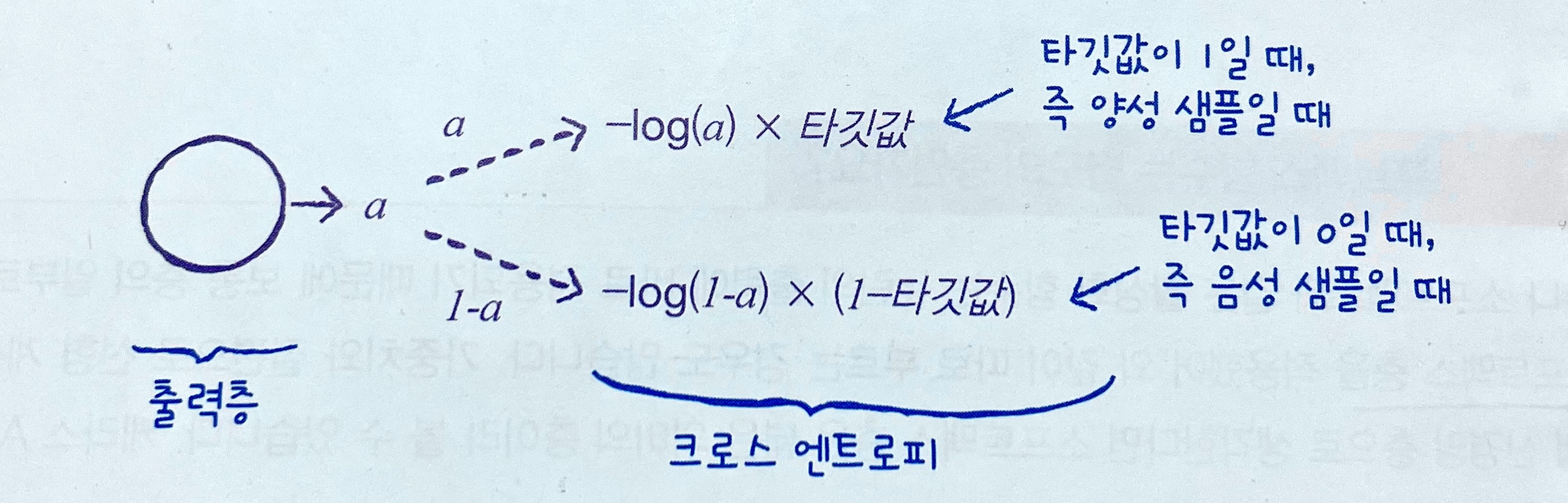
• 4장(205p)에서 배웠던 이진 크로스 엔트로피 손실함수를 돌아보면,
  이진 분류에서는 타깃값이 0, 1 두 개뿐이었음.
  ➡️출력값(예측확률)은 양성클래스에 대한 것(a) 하나뿐이었고, 음성클래스는 (1-a)로 쉽게 구할 수 있었음. ➡️즉, 유닛 1개만으로 양성/음성 손실을 모두 계산할 수 있었음!
  
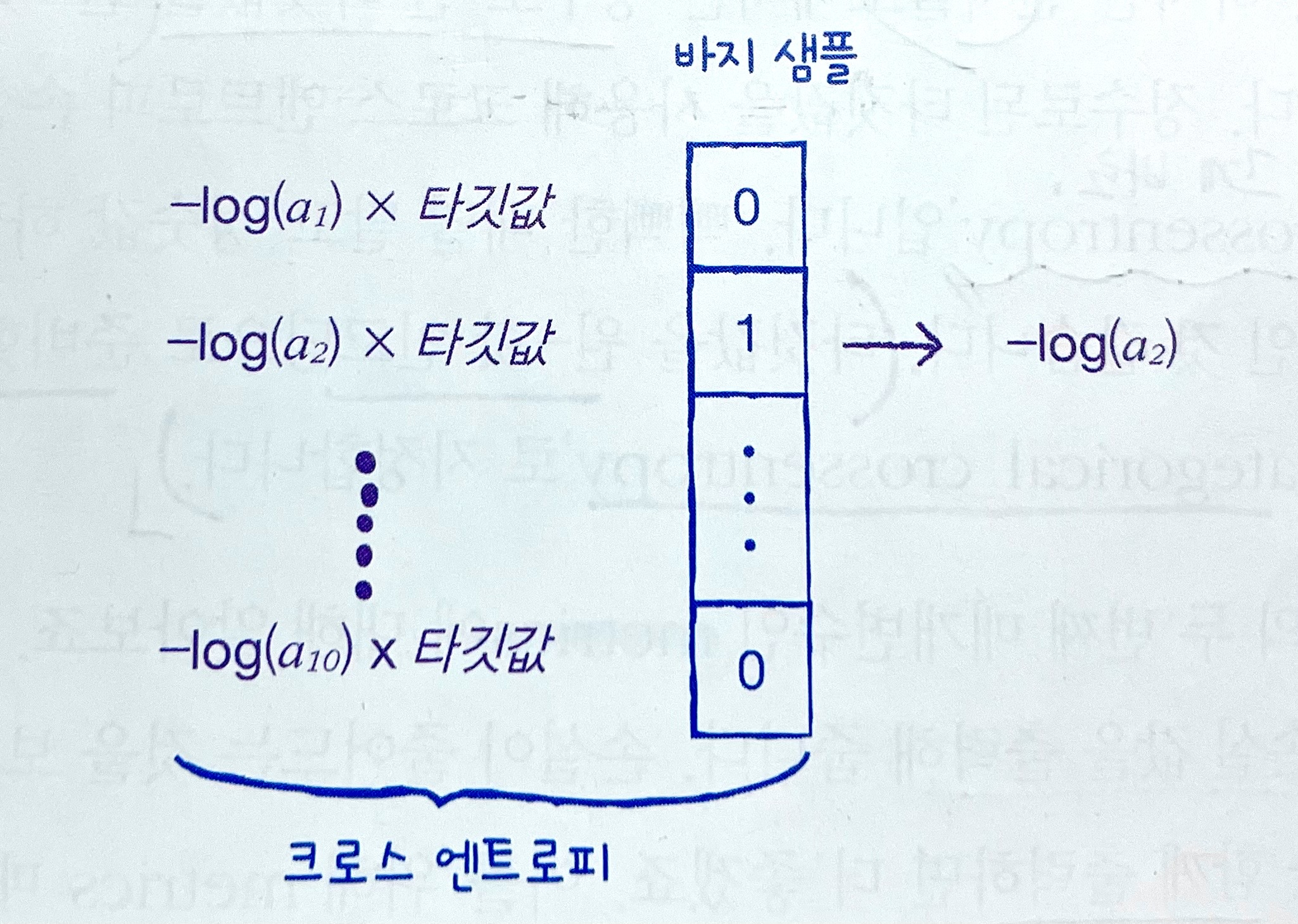
• 반면, 지금같은 다중 분류에서는 타깃값이 0~9처럼 다양함.
  ➡️출력값도 각 클래스에 대한 확률이 (189p처럼) 모두 출력됨. ➡️따라서 깔끔하게 양성 클래스의 확률만 남기기 위해, 양성 확률의 타깃은 1, 나머지 음성 확률의 타깃은 다 0으로 만들어버림 = 이걸 '원-핫 인코딩'이라고 함!
  
• 근데, 텐서플로에서는 원-핫 인코딩 없이 그냥 정수로 된 타깃값을 사용할 수 있음.
  ➡️ 바로 이 때 'sparse'를 붙이는 거임!!!^^
  🆚 그러니 만약 직접 원-핫 인코딩으로 타깃값 준비했다면, 손실함수를 그냥 loss='categorical_crossentropy'로 지정해도 괜찮은 거임.

➌ 확인문제 풀이 (혼공미션)

<1번>
'모델 파라미터'는 알고리즘이 학습하는 내용을 말한다. (🆚'하이퍼 파라미터'는 모델이 스스로 학습하는 게 아니라 사용자가 직접 지정해줘야 하는 내용) 이 때, 인공신경망은 각 뉴런의 가중치(방정식의 계수)와 절편을 학습하여 출력값을 도출한다.
가중치는 입력특성 100개가 일일이 뉴런 10개에 모두 연결되니까 100 x 10 = 1,000개이다.
절편은 각 방정식, 즉 각 뉴런마다 하나씩 붙으니까 뉴런 개수와 똑같이 10개이다.
➡️ 따라서 위 인공신경망 모델이 학습해야하는 모델 파라미터의 개수는 1,000 + 10 = 1,010개로 구할 수 있다.

<2번>
이진분류라면 시그모이드, 다중분류라면 소프트맥스 함수를 사용한다.

<3번>
.compile()메소드에서 손실함수loss와 측정지표metrics를 설정한다.

<4번>
다중분류는 크로스엔트로피 손실함수 즉, categorical_crossentropy를 쓰면 된다. 그런데 정수 레이블을 그대로 사용할 때는 앞에 'sparse'가 붙어야한다. 만일 따로 타깃에 원핫인코딩을 했다면 2번 보기가 답이 될 수 있다.

---

🤔 Hmmmm...

342p. 훈련 세트에서 테스트 세트를 떼어냈는데, 왜 훈련 세트에 60,000개가 그대로 있나요?

👨🏻‍🏫 훈련 세트와 테스트 세트의 크기는 fashion_mnist.load_data()에서 반환된 크기입니다. 데이터셋마다 훈련 세트와 테스트 세트가 따로 있을 수도 있고 함께 합쳐 있을 수도 있습니다. 🆗 그냥 예제 데이터 자체가 원래 그렇게 구성된 걸로 받아들이면 됨 ㅇㅇ.

357p. 원핫 인코딩이 ‘타깃에 해당하는 확률’만 빼고 다 0으로 만드는데, 이게 이전에 언급(208p)해주셨던 OvR과 동일한 것이라고 보면 될까요?

👨🏻‍🏫 OvR은 다중 분류 모델을 훈련하는 한 방법으로 원핫 인코딩과 동일한 개념은 아닙니다.

차이가 무엇인지 도저히 모르겠습니다ㅠㅠ 교재 208p의 OvR 설명과 357p의 원핫인코딩 설명 모두 "해당 클래스만 1이고 나머지는 모두 0으로 둔다"고 이해되는데요,, 원핫인코딩도 다중분류모델의 손실함수를 구성하는 원리인 거 아닌가요..?

👨🏻‍🏫 원핫인코딩은 특성 값을 벡터로 변환하는 한가지 방법입니다. OvR은 이진 분류 모델을 사용해 다중 분류 작업을 수행하는 방법입니다. OvR은 다중 분류 문제의 타깃을 이진 분류처럼 만들지만 원핫인코딩과 다릅니다.

356p. 잠깐만. 근데 이진분류(205p) 때는 음성클래스 아예 무시하지는 않고
$(1-예측확률)$로 방향만 바꿔줬음. 근데 왜 지금 다중분류에서는 음성클래스의 타깃을 다 0으로 싸그리 막아버림???

🤓 To wrap up...

드디어 딥러닝 파트에 들어왔다.. 아직은 큰 차이를 느낄 정도는 아닌 듯한데..
일단 크로스엔트로피 다중분류의 원리를 다시 복습해야겠다 (추후 수정)

이번엔 생선 럭키백(=무게, 길이 등의 특성을 입력 받아 생선 종류 구분)이 아니라, 패션 럭키백(=픽셀값들을 입력받아 패션 이미지 구분)을 만들어야 하는 상황! → 생선 럭키백 때 했듯이 로지스틱 회귀+SGD로 다중분류 모델을 만듦 → 성능 만족스럽지 않으니 딥러닝 모델을 도입해보자 → 케라스로 가장 기본적인 인공신경망 모델(역시 다중분류)을 만듦 → 그 과정에서 크로스엔트로피 손실함수의 계산과정과 원-핫 인코딩을 배움 → 다음 시간에는 층을 더 쌓아서 본격적인 딥러닝 모델을 만들어보자!