Approach to VAE(Variational Auto Encoder)(1)

temp·2021년 10월 9일

Generative Model

목록 보기

7/30

메인 출처 : ★오토인코더의 모든 것(이활석) - NAVER D2★
Tutorial paper:Tutorial on Variational Autoencoders
original paper : Auto-Encoding Variational Bayes

본 글에 첨부한 대부분의 슬라이드는 이활석님의 '오토인코더의 모든 것'의 강의 자료에서 발췌하였음을 밝힙니다.

Apporach to VAE

본 글에서는 VAE(Variational Auto Encoder)가 무엇인지, 어떤 식으로 접근하면 좋을 지를 다룰 예정입니다.
이를 위해, 먼저 통계 추론의 핵심인 MLE의 관점으로부터 딥러닝의 학습을 간단히 다룹니다.
그 후, Auto Encoder와 Variational Auto Encoder의 핵심적인 차이를 살펴본 뒤, 본격적으로 VAE에 대해 기술합니다.

Deep learning from MLE's point of view.

First, There is Back_prop's point of view.

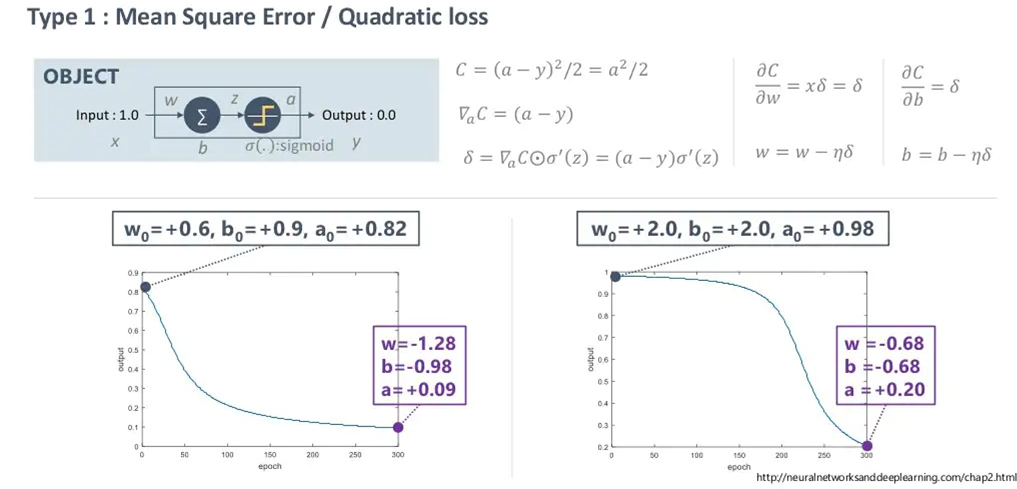
우선, 딥러닝의 학습에 그래디언트를 이용한 역전파 방식이 지배적으로 사용되는 것은 모두 잘 알고 있을 것입니다. 역전파 관점에서 MSE LOSS와 CROSS ENTORPY LOSS의 차이가 위에 나타나 있습니다(Loss: $C$ -Cost).

딥러닝의 학습에 MLE의 접근법을 적용시킬 경우 역전파 기반 방법과 어떻게 차이가 있을 지에 대해 다루어봅시다.

MLE's point of view

여기서는, 네트워크의 출력 값에 대한 해석이 중요합니다.
딥러닝 태스크에서는, 우리가 원하는 출력 $f_{\theta}(x)$ 가 정답과 가까워지기를 희망합니다. 그를 위해 역전파를 이용할 때에는 출력( $f_{\theta}(x)$ )과 정답( $y$ )이 다른 정도를 Loss function으로 정의하고, 두 값의 차이를 줄이는 방향으로 학습을 진행했습니다.

MLE 관점에서는 약간 다릅니다.

네트워크의 출력 값(확률 분포) $f_{\theta}(x)$ 가 주어졌을 때, 정답 $y$ 가 나올 확률(likelihood)가 최대가 되기를 원합니다.

즉, 이 경우 Deep Neural network $f_{\theta}(*)$ 뿐만 아니라, 분포 $p(*|f_{\theta}(x))$ 가 어떤 분포를 따를 지 가정을 하고 가야 합니다.

해당 분포 $p(*|f_{\theta}(x)$ 는 가우시안을 따른다. 혹은 베르누이를 따른다. 등등..

예를 들어, 확률분포 $f_{\theta}(x)$ 가 주어졌을 때 타겟 $y$ 가 나올 확률인 $likelihood$ 를 Gaussian Distribution(가우시안 분포)를 따른다 가정합시다. 또한, 가우시안 분포의 표준편차는 편의상 없다고 가정합시다.

그러면, 실질적으로 Deep Neural Network의 출력 $f_{\theta}(x)$ 은 다름아닌 가우시안 likelihood에 필요한 parameter(평균)을 추정하는 것으로 해석할 수 있습니다.

즉, 네트워크의 출력이 가우시안분포의 '평균'이 됩니다.

이를 나타내는 것이 아래의 그림입니다.

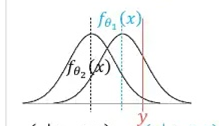
만약 최초의 네트워크의 출력 $f_{\theta_2}(x)$ 이 정해진다면, 이는 가우시안 분포의 평균이라 가정했으므로, 분포 하나가 정해집니다. 이 때, 정답 $y$ 는 fixed point이기 때문에 likelihood $p(y|f_{\theta_2}(x))$ 의 값을 구할 수 있게 됩니다.

그 이후, 도출되는 피드백을 바탕으로 네트워크의 출력이 $f_{\theta_1}(x)$ 로 개선됐다고 합시다. 그러면, 이 경우 또한 개선된 likelihood $p(y|f_{\theta_1}(x))$ 을 얻을 수 있게 됩니다.

그러면, 직관적으로 봤을 때에도 해당 likelihood $p(y|f_{\theta}(x))$ 가 최대가 될 때에는 네트워크의 출력(즉, 가우시안의 평균) $f_{\theta}(x)$ 이 정답 $y$ 과 일치할 때라는 것을 알 수 있습니다.

역전파 관점에서, 네트워크의 출력 값 $f_{\theta}(x)$ 와 정답 $y$ 의 차이를 Loss로 가정하고, 이를 낮추는 방향으로 학습했다면,
MLE 관점에서는, 네트워크의 출력 값 $f_{\theta}(x)$ 를 likelihood의 parameter로 가정한 뒤, likelihood $p(y|f_{\theta}(x))$ 를 최대화하는 방향으로 학습을 하는 것이고, 이는 바로 네트워크의 출력 $f_{\theta}(x)$ 이 정답 $y$ 와 일치할 때 최대가 됩니다.

해당 관점을 유지한 채로, 기계학습을 진행하기 위한 Setting을 살펴보면, 아래와 같습니다.

likelihood $p(y|f_{\theta}(x))$ 를 최대화 하는 것은 log likelihood $log \ p(y|f_{\theta}(x))$ 를 최대화 하는 것과 같으며, negative log likelihood $-log\ p(y|f_{\theta}(x))$ 를 최소화하는 것과 동일합니다. 즉, 이 negative log likelihood를 Loss로 잡고, 최적화를 진행할 수 있습니다.

이 때 $log$ 를 사용하는 것은 역전파를 수행할 때 제약 조건을 만족시키기 위함입니다. 이에 대해서는 강의 '오토인코더의 모든 것 - 1/3'의 초반부를 참고하세요.

수치적 안정성(numerical stability) 또한 이유가 될 수도 있을 것 같습니다.

위와 같이 Loss를 정의하고, 최적화를 수행하면 아래와 같이 최적의 parameter $\theta^{*}$ 를 얻을 수 있게 됩니다.

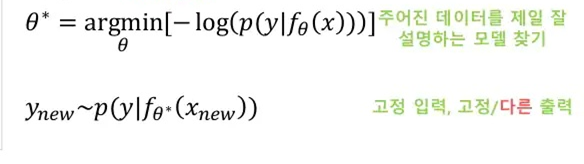
다만, 이게 전통적인 딥러닝 관점(출력 값이 likelihood $p(y_i|x_i)$ )과 다른 점은, 구하고자하는 네트워크의 출력이 바로 특정 분포(의 파라미터)가 된다는 것입니다.

관점만 다를 뿐 결과 자체는 동일합니다.

이처럼 분포를 추정하게 될 경우 얻을 수 있는 이점은 기존의 방식이 고정된 입력을 넣었을 경우 고정된 출력 만을 얻을 수 있는 것과 다르게, 출력이 분포가 되기 때문에 이 분포를 토대로 샘플링을 진행할 수 있게 되는 것입니다.

즉, 잘 최적화가 된 parameter $\theta^{*}$ 가 있을 경우, 고정된 입력을 넣어도 분포를 토대로 다양한 출력을 이끌어낼 수 있고, 이는 추후에 서술할 VAE가 MLE관점을 주로 채택하는 이유가 되기도 합니다.

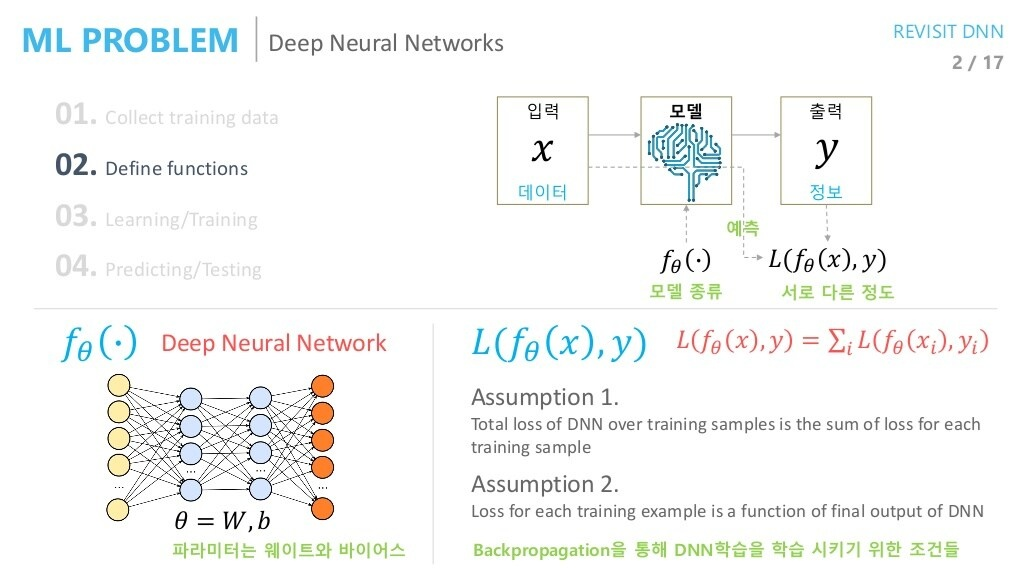
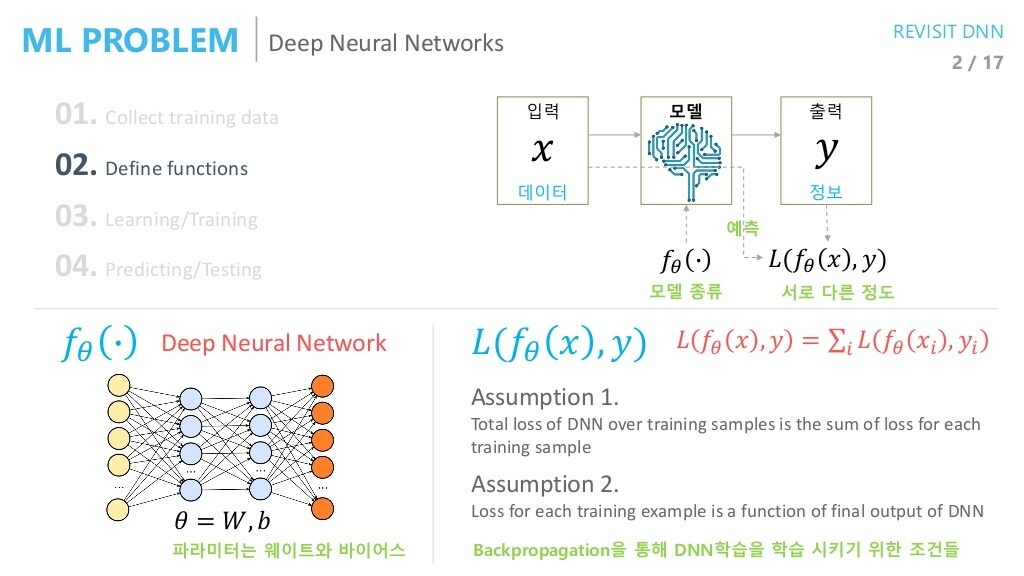
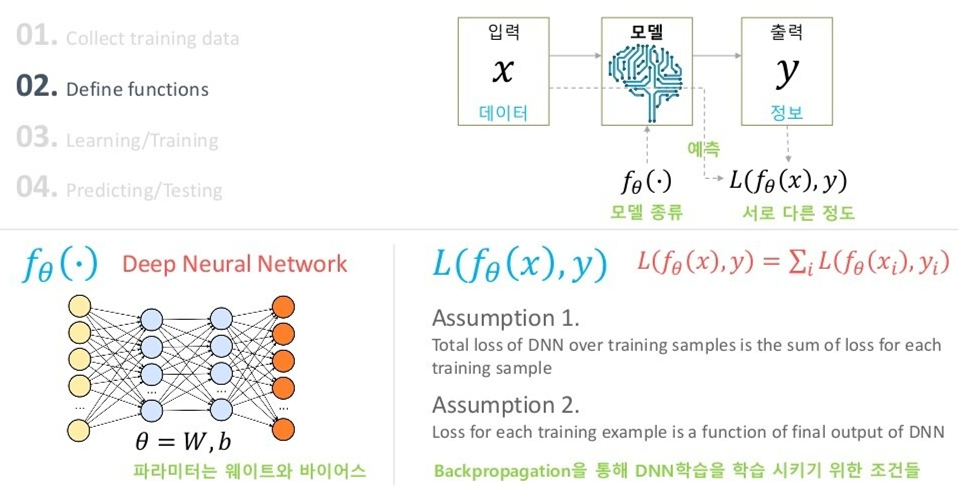
위에서 정의한 Loss인 negative log likelihood가 학습을 위한 두 조건을 충족시키는지를 봅시다.

$i.i.d$ Condition on $p(y|f_{\theta}(x))$ 를 가정할 경우

즉,

sample, 즉 $x_i$ 들이 독립을 이룬다.
각 sample 별로 다른 분포를 따르지 않고 모두가 같은 분포를 따른다.

를 만족할 경우 Deep Neural Network의 2가지 조건을 아래와 같이 만족시킬 수 있습니다.

아무튼, 네트워크의 출력 값을 확률분포의 parameter로 생각한다는 것입니다.

그러면, MLE 관점을 채택했을 경우 Backpropagation 관점이랑 결과가 어떻게 달라질까?

위와 같이 네트워크의 출력 분포를 정규분포로 가정했을 때와, 베르누이 분포로 가정했을 때 likelihood를 전개해보면, 결과적으로 MSE LOSS와 Cross-entropy와 같아지는 것을 볼 수 있습니다.

즉, 결론적으로는 MLE 관점이나 Backprop 관점이나 같습니다.

위에서, $f_{\theta}(x_i)$ 의 출력 값은 특정 분포의 모수이고, 여기서 특정 분포는 label $y_i$ 의 분포를 말합니다. 물론 이미지의 경우 $y_i$ 가 거의 continuous한 분포를 갖지만, binary한 분포를 갖는다 가정하는 것이 성능이 더 좋을 때가 있다고 합니다.

(multivariate cases)

다만, MLE관점에서 어떤 Loss를 쓰는 것이 좋을 지를 판단해봅시다.

이는 negative log likelihood에서 $y_i$ 의 분포에 따라 정해질 것입니다.

즉, $y_i$ 의 분포가 Gaussian에 가깝다면(즉, $y_i$ 가 continous 하다면) MSE loss를 쓰는 것이 타당하고,
$y_i$ 의 분포가 Bernoulli에 가깝다면(즉, $y_i$ 가 discrete 하다면) Cross Entropy Loss를 쓰는 것이 타당합니다.

그렇기 때문에, Continous Value에 대해 MSE loss를 쓰는 이유는 '네트워크의 출력 값이 Gaussian에 가깝다고 가정할 것이기 때문에' 라고 철학적으로 해석할 수 있는 것입니다. 마찬가지로 Classification task의 경우에는 출력 값이 discrete하기 때문에 Cross entropy를 사용한다고 볼 수 있는 것입니다.

즉, MLE 방법을 토대로 Loss를 설정하고 학습을 진행하더라도, 엄밀한 확률 분포에 대한 고려를 모델에 포함하지 않고, Cross entropy(or MSE) loss로 학습을 진행해도 됩니다.

정규분포와 베르누이분포 외의 가정도 할 수 있지만, 수학적으로 복잡합니다. 다만, 딥러닝에서도 MSE와 Cross-entropy 외에 다른 Loss를 사용할 수 있는 만큼, 다른 분포에 대한 고려를 하는 것 또한 의미가 있다고 생각할 수 있습니다.

(네트워크의 출력 값이 likelihood가 되는 게 아닌, 분포의 parameter가 된다는 그림)

아래는, 벤지오 교수의 발표자료에 해당하는 슬라이드이다.

$P(Y|X)$ 를 추정하고 싶다.
$P(Y|X)$ 를 추정하기 위해 $P(Y|\omega=f_{\theta}(X))$ 로 파라미터화하자. 여기서 parameter $\omega$ 를 구하는 task로 변한다.
negative log likelihood로 loss를 정하자.
( $Y$ 를 가우시안으로 가정할 경우), 분포의 평균 $\mu$ 를 네트워크의 $output$ 으로 설정한다. 이 output은 입력 $X$ 에 따라 결정된다. 그러면 Loss를 위와 같이 MSE와 비슷한 꼴로 바꿀 수 있다( $\sigma$ =1이 보통 쓰인다).
$Y$ 를 베르누이(혹은 이항분포)로 가정할 경우 위와 같이 Loss를 Cross-entropy와 비슷한 꼴로 바꿀 수 있다.

위의 2. Parametrize $P(Y|X)$ $=$ $P(Y|\omega=f_{\theta}(X))$
에서, 등식이 성립하려면 $f_{\theta}(X)$ 가 deterministic function일 필요가 있습니다.

AutoEncoder vs Variational AutoEncoder

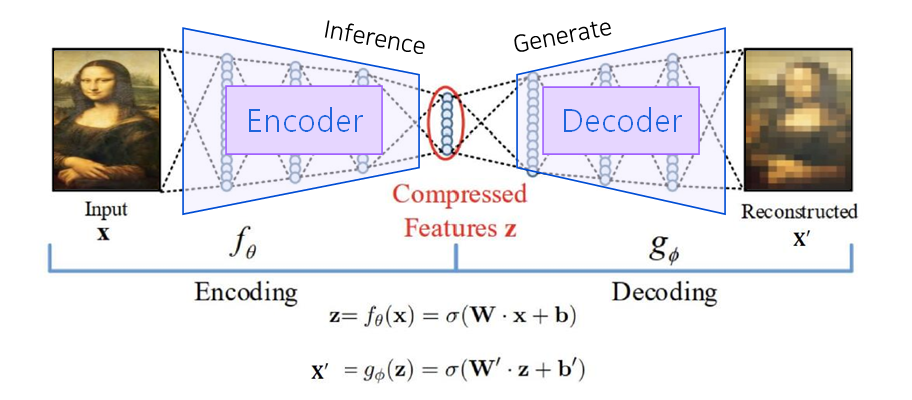
오토인코더는 위에서 보다시피, 특정 input이 주어졌을 때의 상황(output을 input에 가깝게 복원)을 다룹니다. 즉, 차원을 잘 축소하기 위해(매니폴드를 잘 학습하기 위해) Input $x$ 라는 target을 decoder에 부여하여 Supervised Learning을 진행한 것 뿐이지, Decoder는 사실상 우리의 관심 대상이 아닙니다.

반면, 후에 서술할 VAE는 그저 Dataset의 분포를 학습하여 이를 토대로 샘플 생성(Generate)을 잘 하는 것을 목표로 합니다. 즉, 이 때는 Decoder가 굉장히 중요한 역할을 합니다.

Manifold Learning

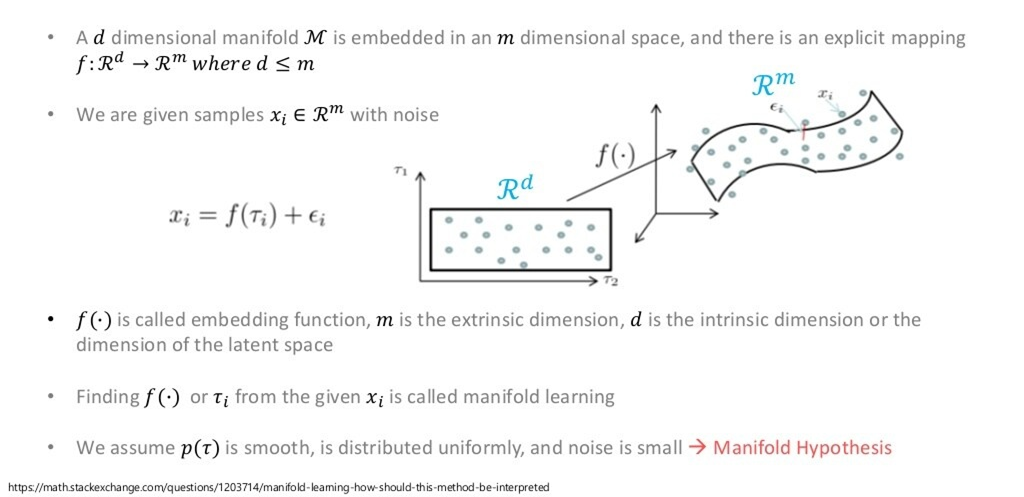
위의 그림에서는 $m$ 차원을 $d$ 차원으로 줄이는 과정이 담겨 있습니다.
편의상 그림에서는 $m=3$ , $d=2$ 지만, 실제로 $m$ 은 훨씬 더 고차원입니다.
가령, image dataset이라면 $m=224\times224\times3$ 과 같은 차원으로 이루어져 있을 것입니다.

이 때, 각 data sample을 해당 공간에 뿌리게 되면 고차원 공간의 point가 생기는 것을 볼 수 있습니다. 여기서, Manifold란 $m$ 차원의 data sample들을, $m$ 보다 더 작은 sub space에서도 error 없이 다룰 수 있는 공간을 말합니다.

즉, 고차원 공간에서 데이터를 잘 아우르는 저차원 Manifold를 잘 찾을 수 있다면, 해당 manifold를 잘 펼쳐서 차원 축소를 진행할 수 있다는 개념입니다

원래의 데이터 특성을 잘 유지하는 방향으로 차원을 축소시키는 것이 매니폴드 러닝의 근본적인 목표입니다.

Curse of dimensionality

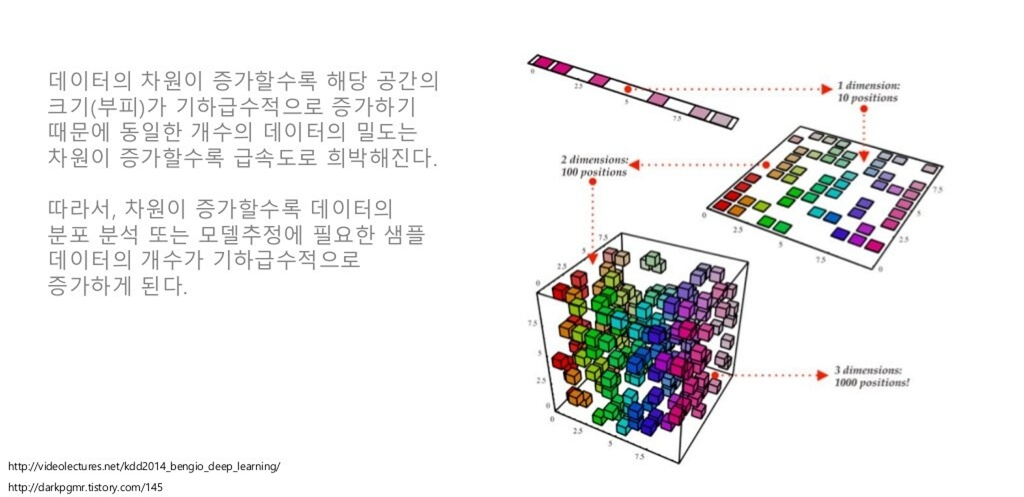
데이터 차원이 증가할 수록, 위처럼 데이터의 밀도는 희박해질 수밖에 없기 때문에 학습, 예측 등이 정상적으로 모델링 될 수가 없습니다.

하지만, 아래 그림과 같이 고차원 데이터는 저차원의 매니폴드로 잘 아우를 수 있을 것이라고 가정을 하고 진행을 합니다.

Manifold?

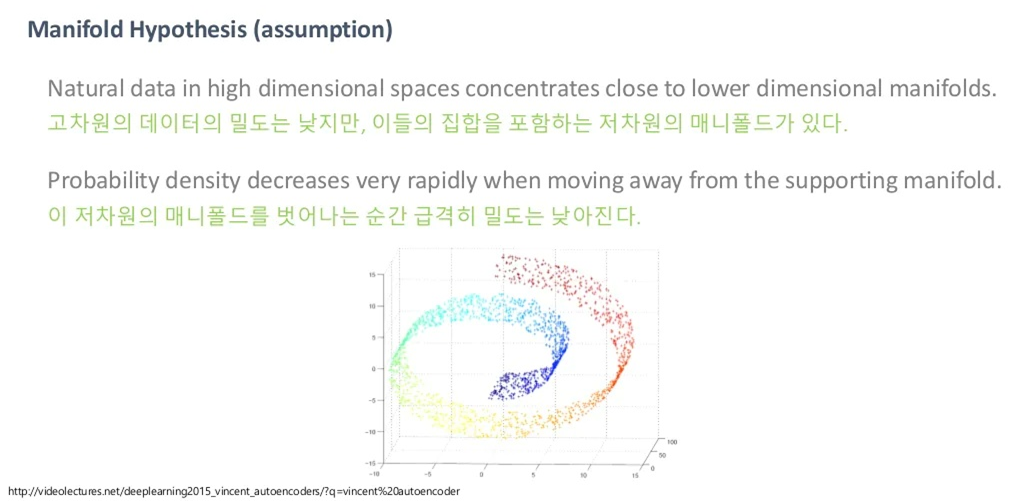
만약 저차원의 매니폴드로 아우를 수 있는 게 아니라, 고차원 공간에 골고루 퍼져 있다고 가정합시다. 그러면, Uniform sampling을 굉장히 많이 했을 때 의미 있는, 즉 semantic 한 이미지를 한 번이라도 볼 수 있어야 합니다. 하지만, 우리가 얻을 수 있는 건 오로지 노이즈밖에 못 볼 것입니다. 아무리 많이 샘플링을 한다 해도, 의미 있는 이미지를 얻을 수 없습니다.

그렇기 때문에, 위처럼 얼굴, 스케치, 문자 등이 어느 한 곳에 가까이 몰려 있을 것이라고 생각합니다.

그래서 결국 저차원 manifold를 잘 찾아낸다는 것은, 데이터를 잘 아우르는 저차원 manifold의 분포를 토대로 sampling을 할 수 있다는 것이고, 이로부터 새로운 data sample을 생성할 수 있게 됩니다.

200x200이 작아보이지만 사실상 엄청난 공간을 다루고 있는 것. 200x200일지라도 해당 차원에서 다양한 class들을 아우르는 manifold 찾기는 굉장히 어렵고, 적어도 도메인을 한정 지어야만 의미 있는 manifold를 찾을 수 있을 것(2018년 기준).

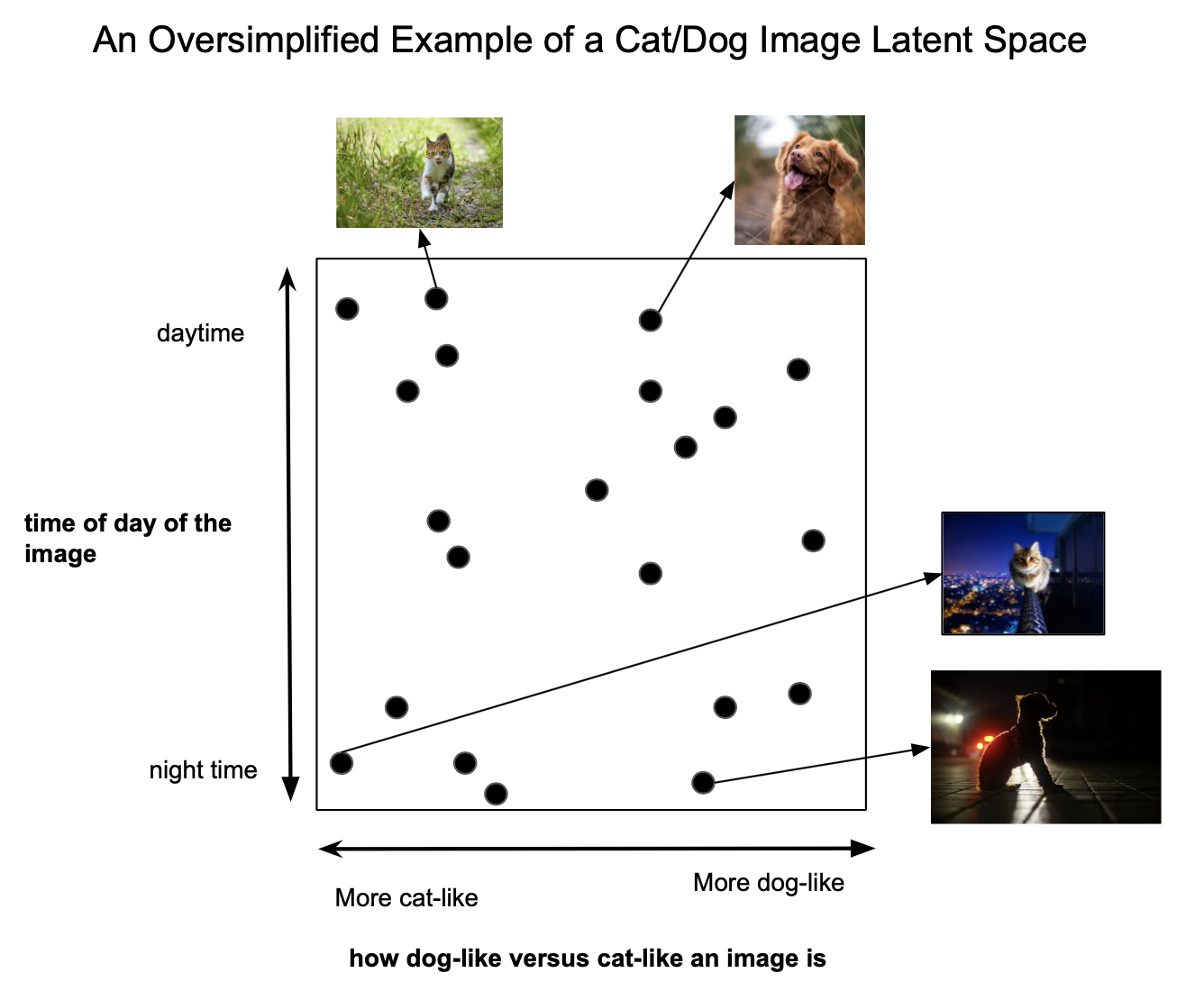
반면, 매니폴드를 잘 찾는다는 것은, 아래와 같이 의미 있는 feature(representation)을 찾는다는 것과 같습니다.

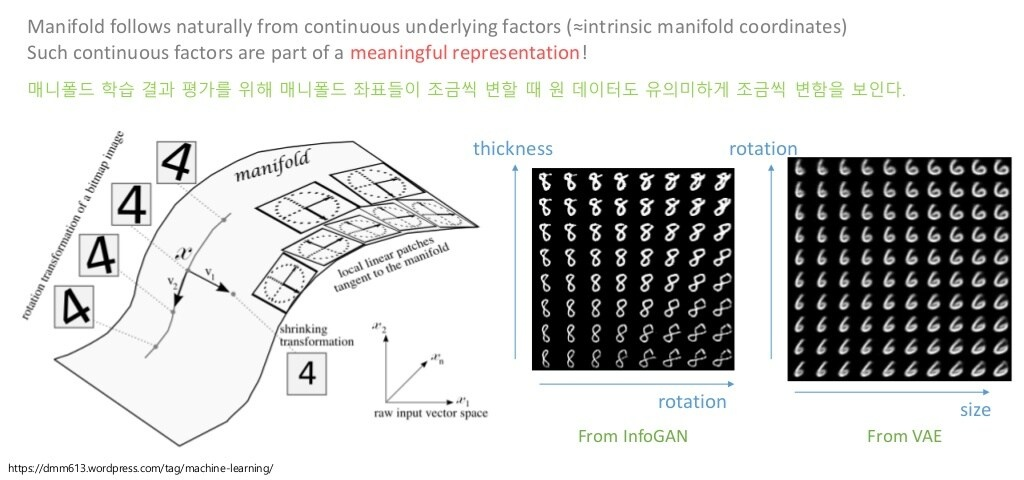
즉, manifold에서 좌표가 조금 변한다면, 원 데이터 또한 유의미하게 바뀔 것이라 가정합니다(그림에서 글자의 두께, 회전, 크기 등).

당연히, Unsupervised Learning이기 때문에 의미 있는 feature들은 자동으로 찾는 것이 목표입니다.

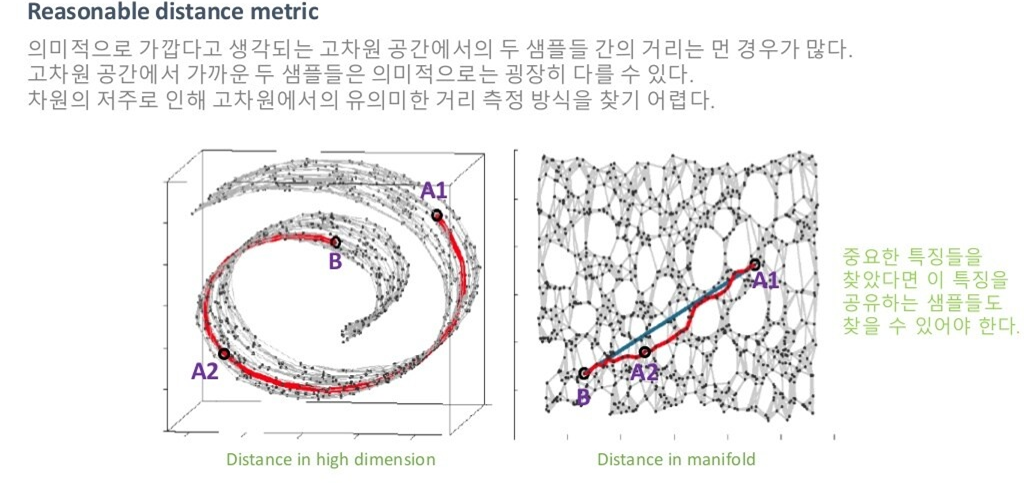
위의 그림을 살펴봅시다.
같은 거리 metric을 사용하더라도, 저차원 공간에서의 거리와 고차원 공간에서의 거리는 다를 수 있습니다. 즉, 고차원 공간에서 가깝더라도, 의미적으로는 가깝지 않을 수 있습니다. 저차원 매니폴드가 이미지의 의미 있는 feature를 잘 담고 있다고 가정하니까, 저차원 공간에서 가까운 것이 오히려 의미 있는 distance metric이라고 할 수 있는 거죠. 당연히 매니폴드를 잘 못 찾았다면 거리 개념이 잘 작동하지 않겠지만요.

예시로 보겠습니다.

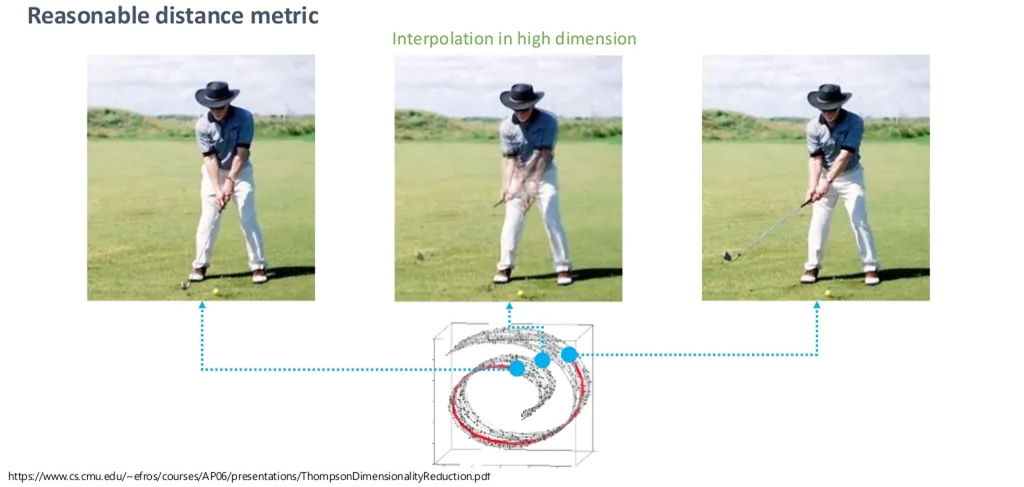
위처럼, 매니폴드에서 벗어나는 순간 큰 의미가 없는 단지 원래 공간의 픽셀 값의 중간 값만을 반환합니다.

하지만, 매니폴드를 잘 찾았다는 가정 하에서 매니폴드 공간에서의 중간 값을 취한다면, 훨씬 semantic한 sample을 찾을 수 있을 것입니다.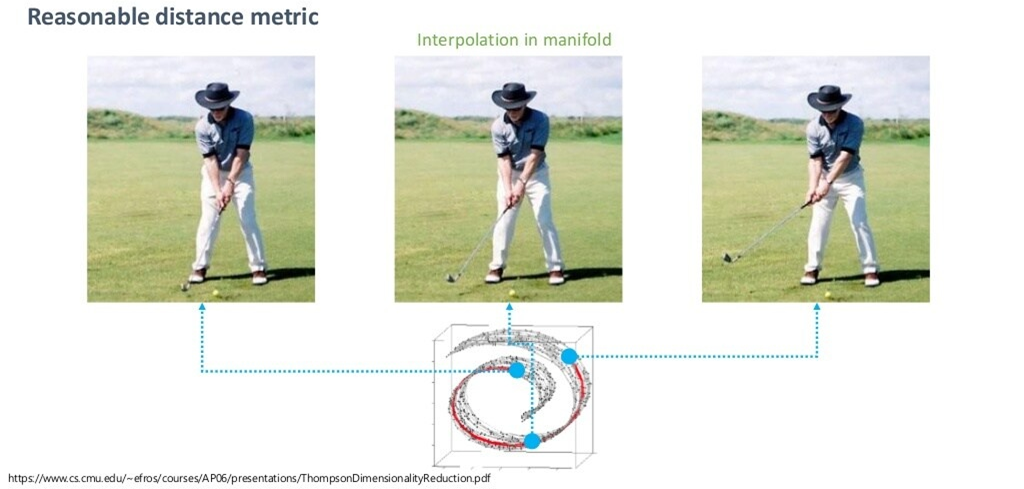

Entangled vs Disentangled in Manifold

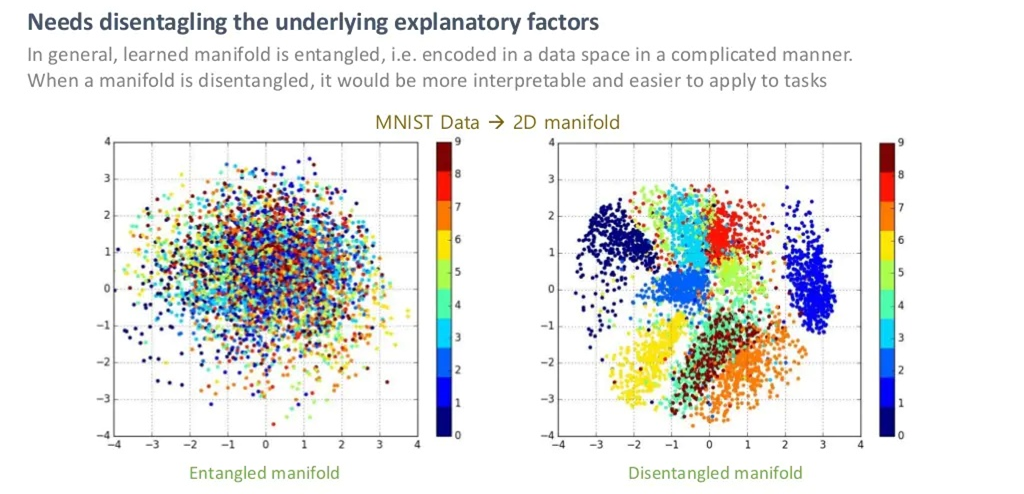
28x28차원의 MNIST Data를 2차원 매니폴드에서 봤을 때, 위 그림의 왼쪽처럼 1~9의 숫자가 잘 나뉘어 있지 않다면 이를 Entangled 하다고 하며, 그림의 오른쪽처럼 1~9가 잘 나뉘어 있다면, 이를 Disentangled하다고 합니다.