메인 출처 : 오토인코더의 모든 것(이활석) - NAVER D2
Tutorial paper:Tutorial on Variational Autoencoders
Code: github.com/hwalsuklee/vae
original paper : Auto-Encoding Variational Bayes

VAE

Variational Auto Encoder의 저자인 King. ma는 Adam optimizer 또한 개발했다고 합니다. 수학적으로 수준이 높은 저자다 보니, VAE의 original 논문 또한 이해하기가 상당히 힘들다고 합니다.

Code를 보게 되면 AutoEncoder와 크게 다를 것 없어 보입니다. 하지만, 논문의 흐름을 따라 가면 완전히 다른 모델을 볼 수 있을 것입니다. 즉, VAE는 엄밀히 따지면 AutoEncoder와는 다른 모델입니다.

왜냐면, AutoEncoder는 애초에 input을 잘 압축(즉, 매니폴드를 잘 학습)하는 것이 최종적인 목표이고, 이를 위해 Decoder에 Target(Input과 동일)을 주어서 Supervised Learning을 진행했을 뿐입니다. 즉, Decoder에는 관심을 두지 않습니다.
VAE는 샘플 Generate를 잘 하는 것이 목표기 때문에 Decoder가 주요 관심 대상이 되고, Encoder는 그를 위한 수단일 뿐입니다.

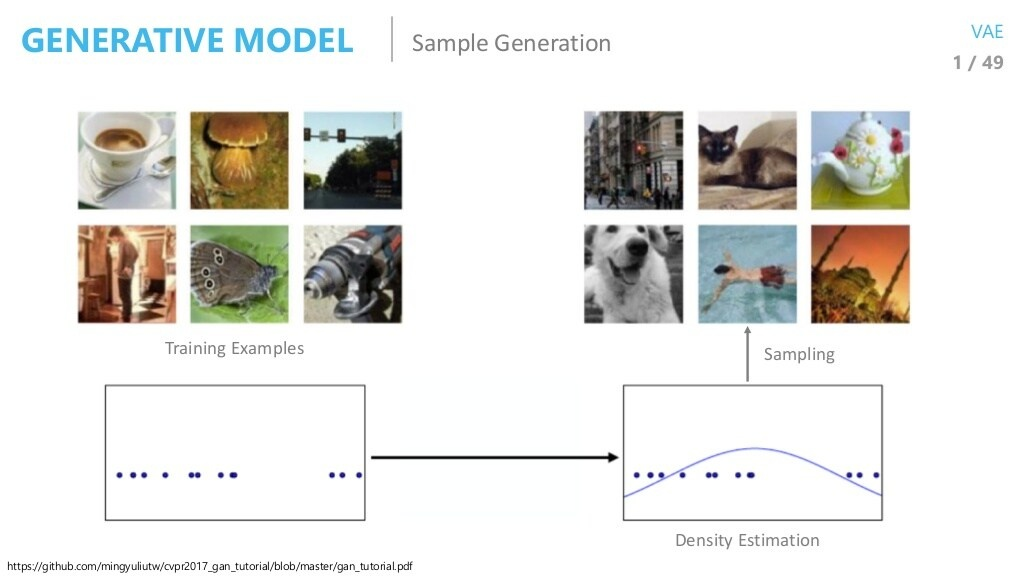
Sample Generation

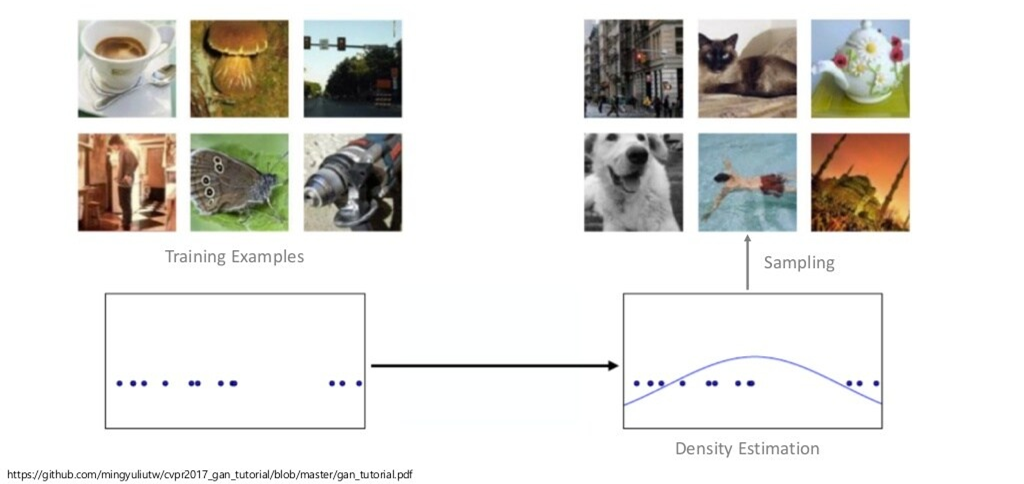
(생성모델의 목적은 Dataset의 data sample들을 이용해, 해당 sample들을 잘 표현하는 확률 분포를 학습하는 것)

만약 Dataset의 분포를 잘 학습할 수 있다면, 해당 분포로부터 새로운 data sample 또한 잘 생성할 수 있겠죠?
수식으로 나타내면, 아래와 같습니다.

최종적인 목표를 위해, 우리는 잠재벡터 $z$가 주어졌을 때 데이터 sample $x$가 나올 likelihood를 가장 최대화하는 방향으로 학습하고 싶습니다.

이 때, Dataset의 분포를 무작위하게 모사하는 것 외에도, 분포를 잘 학습해서 우리가 원하는 feature를 조절할 수 있으면 더욱 좋을 것입니다. 즉, 잠재 벡터 $z$를 remote controller 정도로 볼 수 있습니다. $z$의 특성을 약간 바꾸어 우리가 원하는 새로운 data sample $x'$를 만들 수 있으니까요.

아무튼, 해당 잠재 벡터 $z$를 사전 분포 $p(z)$에서 샘플링하고, 결정적(Deterministic) 함수인 $g_{\theta}(*)$에 태우면 확률 분포의 parameter를 반환합니다. 그렇기 때문에 $p_{\theta}(x|z)$를 $p(x|g_{\theta}(z))$와 같이 해석할 수 있습니다($g_{\theta}(z)$ : 분포의 parameter).

그러면, 우리가 원하는 Train DB에 대한 확률 분포 $p(x)$를, $\int p(x|g_{\theta}(z))p(z)dz$를 통해 얻을 수 있게 됩니다. $p(z)$는 우리가 정의하는 사전 분포이기 때문에 알 수 있고, $g_{\theta}(z)$ 또한 샘플링한 $z$와 결정적 함수 $g_{\theta}(z)$(Neural Net)를 통해 알 수 있으니까요.

이 때, $z$를 다루기 쉬운 확률 분포에서 뽑아야 우리가 제어하기도 편하기 때문에 $p(z)$를 보통 가우시안분포나 균등분포와 같은 쉬운 분포로 정의합니다.

Q1. 사전 분포를 다루기 쉬운 분포로 정의하면 복잡한 매니폴드를 잘 표현할 수 있을까요?

우리가 제어하고자 하는 잠재벡터 $z$는 매니폴드 상에서의 값들입니다.
이전의 글에서 봤다시피 매니폴드 또한 굉장히 고차원의 공간이기 때문에 복잡할텐데,
이런 $z$를 정규분포에서 샘플링하게 되면 이런 복잡한 매니폴드를 잘 표현할 수 있을까요?

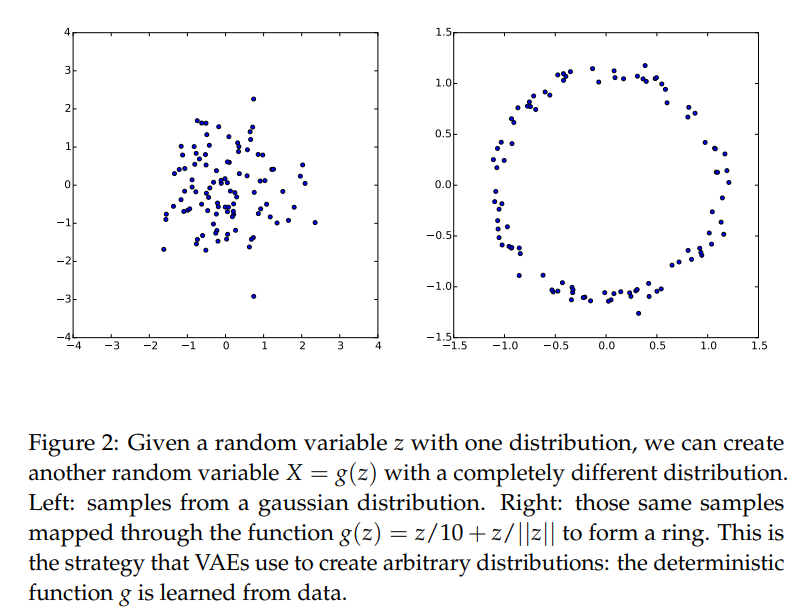
(Figure in Tutorial on Variational Autoencoders)

A. 어차피, Deep Nerual Net은 굉장히 복잡합니다. 그렇기 때문에 Deep Neural Net의 초반 Layer는 충분히 복잡한 매니폴드를 표현하기 위한 역할을 취할 수 있습니다(수학적으로도 잘 증명됐겠죠 뭐..).

Q2. 그냥 p(x)를 최대화하기 위해서 MLE(Maximum Likelihood Estimation)을 적용하면 안되나요?

즉, $p(x)\approx \sum_{i} p(x|g_{\theta}(z_i))p(z_i)$로 생각해서,
(우변의 식들은 모두 알 수 있으므로)
적당히 결과 값을 몬테카를로 샘플링해 근사화하면 안되나요?

(Figure in Tutorial on Variational Autoencoders)

A. $x$는 Training DB의 sample하나 입니다. 즉, 이는 실제 샘플이기 때문에 $p(x)$ 또한 높게 나와야 합니다.

위 그림의 우측 (a),(b),(c)를 보면, (a)가 원본 이미지 $x$, (b)는 $x$에서 약간의 픽셀을 자른 이미지, (c)는 (a)의 화소를 오른쪽으로 한 칸씩 미룬 이미지입니다.

의미적으로는 (a)와 (c)가 훨씬 가까울 것입니다.

하지만, MSE 관점에서는 (a)와 (b)가 훨씬 가깝습니다.
이게 왜 문제가 되냐면,
$p(z)$를 가우시안 분포로 가정하고 $z$를 샘플링해 학습을 시켰을 경우,
(MLE 관점에서의 가우시안 분포가 Back propagation 관점에서의 MSE Loss와 같았기 때문에 - $g_{\theta}(z_i)$와 $x$ 사이의 MSE,)
(c)보다는 MSE loss가 더 좋은 (b)의 분포에서 훨씬 샘플링이 많이 되기 때문입니다.

즉, (a)와의 likelihood는 의미적으로 거리가 먼 (b)가 $p(x)$ 대신 구한 평균 $\sum_{i} p(x|g_{\theta}(z_i))p(z_i)$에 해당할 때 더 높게 찍힙니다. 평균이 (b)에 가까울 때 샘플링을 하다보면 결국 의미적으로 좋지 않은 표본이 나올 확률이 커집니다.

MSE에 따라 학습을 시키다 보면 평균이 (b)에 가까워질 것이고, 그 곳에서 샘플링을 하게 되면 (b)와 가까운 샘플들이 나옵니다.

위에서, 가우시안을 가정했을 경우 $p(x|g_{\theta}(z))$는 $N(x|g_{theta}(z), \sigma^2*I)$를 따르는데, 이에 대해서는 Tutorials for VAE를 참고하면 자세히 알 수 있습니다.

그렇기 때문에 우리는 $p(z)$를 가우시안분포로 가정한 뒤 단순하게 $z$를 $p(z)$에서 뽑아 학습을 진행하면 안됩니다.

---

ELBO

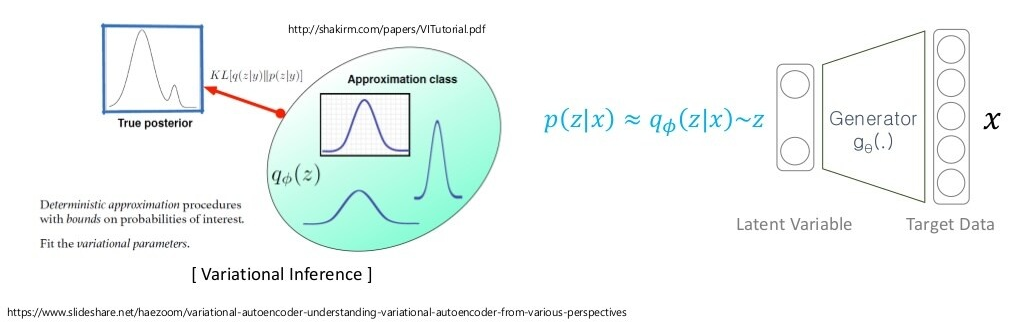
한 가지 가능한 해법은 $z$를 $p(z):Gaussian$에서 샘플링하는 것 말고, $x$와 유의미하게 유사한 샘플이 나올 수 있는 $p(z|x)$로부터 샘플링하는 것입니다.
단, $p(z|x)$를 모르기 때문에, 우리가 알고 있는 분포(Approximation class) $q_{\phi}(z|x)$를 택해서, 그 분포의 파라미터 값을 최적화함으로써 true posterior $p(z|x)$에 제일 가까운 분포를 만듭니다.
여기서, 분포의 파라미터($\phi$)를 조정하기 때문에 Variational Inference란 단어가 쓰이는 것입니다.

다시 말하자면, 일반적으로 AutoEncoder 방식으로 학습을 한다면 $z$는 여차저차 찾을 수는 있는 반면, Decoder의 성능이 좋지 않아 현실 Dataset에 맞는 샘플 $x$를 잘 생성할 수는 없습니다.
하지만, 좋은 Generation 할 수 있게끔, 이상적인 true posterior $p(z|x)$에 가까워지도록 설계된 샘플링 함수 $q_{\phi}(z|x)$ 의 파라미터를 잘 조정해가면서 $z$를 해당 샘플링 함수에서 뽑아 학습을 진행한다면 $x$에 가까운 좋은 샘플이 잘 나올 수 있을 것입니다.

---

잠깐 정리하면, 우리가 궁극적으로 원하는 함수는
$p(x)$ 였습니다. 이를
$p(x)=\int p(x|g_{\theta}(z))p(z)dz$로 바꿔 구할 수 있었고,

여기서 $z$를 prior $p(z)$로부터 단순하게 샘플링하면 문제가 생겼으므로, true posterior $p(z|x)$에 가까운 approximation class $q_{\phi}(z|x)$를 정의해서 $z$를 샘플링 하려고 했습니다.

여기서, 우리는 이들($p(x), p(z), p(z|x), q_{\phi}(z|x)$) 간의 관계식을 찾은 뒤, Loss function을 정해야 합니다. 구할 수 없는 식들을 구할 수 있는 식들로 나타내야 하니까요. 다만 이 과정에서 완벽한 loss를 찾기는 힘들고, 편의를 위해 특정한 가정을 함으로써 식을 전개해나가는 일이 부지기수입니다.

조금 뜬금 없지만, NLP분야의 연구 Show, Attend and Tell: Neural Image Caption Generation with Visual Attention에도 이와 비슷한 관점이 사용됩니다.

(목적함수 $log \ p(y|a)$대신 Lower bound $L_s$를 잡아 새로운 목적함수로 사용하는 모습 - approximate variational lower bound)

---

결론적으로, 위에서 중요하게 살폈던 term들 간의 관계를 나타낸 식이 ELBO : Evidence Lower BOund입니다.
여기서, Evidence의 단어 자체가 큰 의미를 갖는데, 특정한 정보를 주기 때문입니다.

ELBO 유도 (1)

• $p(x)$를 최대화 하기 위해 $log \ p(x)$를 최대화하거나 $-log \ p(x)$를 최소화합니다.
• 주변확률 분포($p(x)=p(x|z)p(z)$)를 이용하고, 젠센 부등식을 활용해 Lower bound를 잡을 수 있습니다.

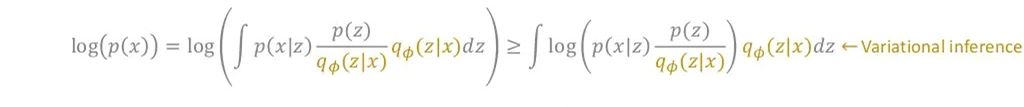
• $p(x|z)$ 대신 $z$를 샘플링해줄 $q_{\phi}(z|x)$를 포함한 식으로 변경시켜줍니다(Variational Inference).

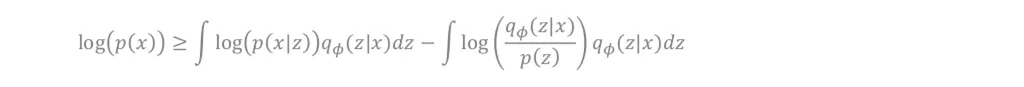
• 그 후 마지막 식의 $log$ 내 항들을 전개해줍니다.

• 그러면, 최종적으로 위와같은 식으로 변경해줄 수 있습니다.

즉, $p(x)$를 최대화하기 위해서 $ELBO(\phi)$값을 최대화해줍니다.

과연 Lower bound를 최대화하는 것만으로 $p(x)$의 최대화 문제를 대체할 수 있을 까요? 이에 대해 정확한 이해를

ELBO 유도 (2)

위 식에서, $p(x)$는 우리가 최대화하고자 하는 상수 값으로 보고 고정할 수 있습니다($x$ : target image). 또한 우리의 목표는 approximation class $q_{\phi}(z|x)$를 $p(z|x)$에 가깝게 하는 것이이기 때문에, 두 분포 간의 차이를 나타내는 term인 $KL(q_{\phi}(z|x)||p(z|x))$은 최소가 되어야 합니다. 즉, $ELBO(\phi)$를 최대화하면 됩니다.

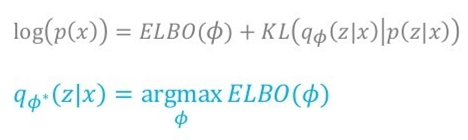
즉, 목표는 $ELBO$ 값을 최대화하는 것으로 바뀌게 되고, $ELBO$ 유도 (1)에서 봤다시피 $ELBO$ 식은 아래와 같이 기댓값(평균값)과 KL term으로 나뉩니다.

위의 그림에 써있다 시피, $log\ p(x)$를 전개했을 때 ELBO와 KL term으로 나눠졌고, 그 때의 KL term에는 $p(z|x)$가 쓰인 반면, $ELBO$ 를 전개해 기댓값과 KL term으로 나눠졌을 때의 KL Term에는 $p(z)$가 쓰입니다.
즉, $log \ p(x)$를 최대화하는 문제를 $ELBO$ 값을 최대화하는 문제로 확대해 바라볼 경우, $KL(q_{\phi}(z|x)||p(z))$는 작아지게끔 학습이 되며, 결론적으로 잘 학습이 됐다면 $z$를 $q_{\phi}(z|x)$에서 샘플링하지 않고 간단한 가우시안 prior인 $p(z)$로부터 샘플링해도 괜찮은 generation 결과를 볼 수 있습니다.

---

Loss

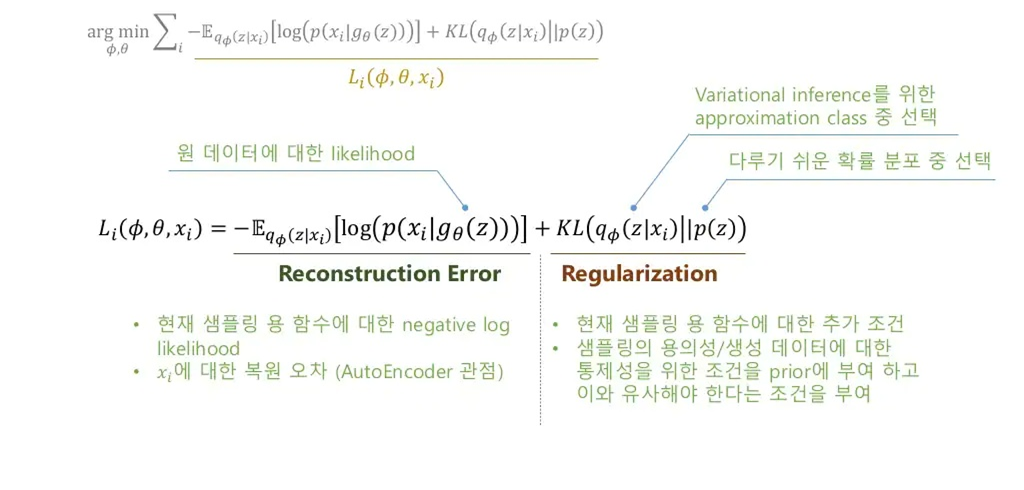
정리

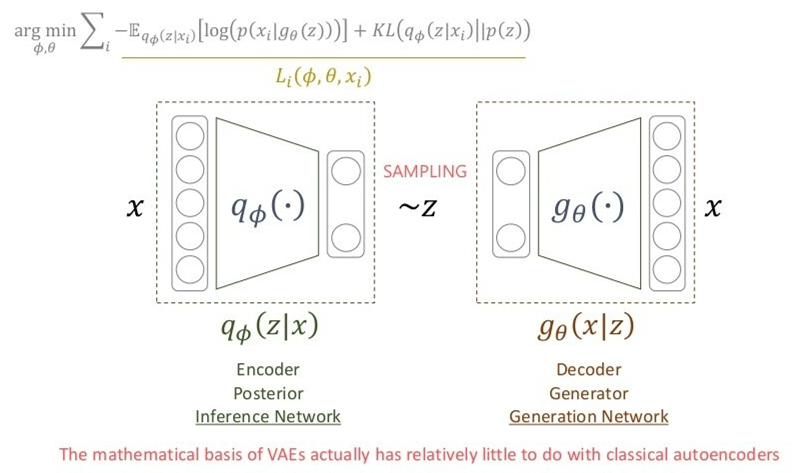
• $p(z)$에서 $z$를 샘플링했더니 생성이 잘 안 됨
• input $x$에 대한 정보를 받은 $p(z|x)$에서 $z$를 샘플링하고 싶음.
• $p(z|x)$는 모르니까 $q_{\phi}(z|x)$를 최적화해서 사용할 것임.
• 즉, $\phi$를 활용하기 위해 $ELBO$ term을 최대화하는 $\phi$를 찾을 것임.
• 추가로, $g_{\theta}(x|z)$에서도 $x$와 유사한 샘플을 생성할 확률을 높힐 $\theta$를 구해야 하는데, 그것 또한 $ELBO$ term의 첫 항에서 고려됨.

즉, $ELBO$ term을 $\phi$에 대해서 최적화할 경우 좋은 샘플링 함수를, $\theta$에 대해서 최적화할 경우 좋은 generator를 얻을 수 있게 됩니다.
(같은 Loss 함수를 사용하지만 결국 $\phi, \theta$에게 모두 이롭게끔 학습됩니다)

---

자세한 내용은 understanding-variational-autoencoders-vaes를 참고하세요.

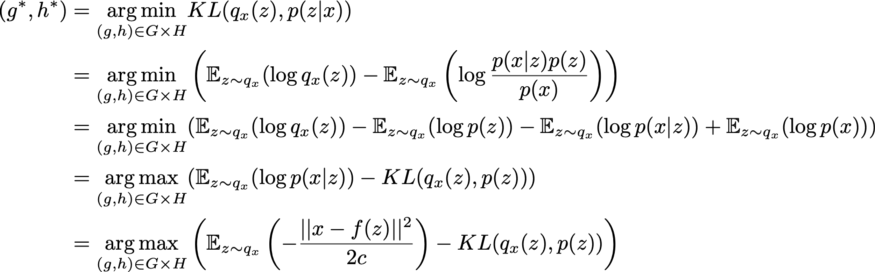
여기서 $f$: Gaussian decoder, $g,h$ : encoder(평균/ 분산)

---

좌측의 Reconstruction Error term은 AutoEncoder와 같은 term으로, 해당 분포가 어떤 분포(가우시안 or 베르누이)를 따르느냐에 따라 MSE or Cross Entropy loss로 갈립니다. likelihood이므로 높아지게끔 학습이 진행됩니다.
우측의 Regularization term은 Reconstruction Error가 좋을 경우 이왕이면 Approximation class $q_{\phi}(z|x)$가 prior $p(z)$와 유사했으면 좋겠다는 생각을 반영하는 term입니다. $z$를 샘플링할 분포는 (표준정규) prior $p(z)$와 같이 다루기 쉬워야 하니까요.

이제, KL-Divergence term을 계산해봅시다.

---

KL-Divergence term

위에서, prior $p(z)$와 approximation class $q_{\phi}(z|x)$는 정규분포로 가정했습니다.

좋은 sampling함수를 찾는다는 것은 $\phi$, 즉 정규분포(가우시안분포)의 평균과 분산을 찾는 것과 같습니다.

두 분포가 가우시안으로 같기 때문에, 아래와 같이 구해진 공식을 토대로 KL term은 closed form으로 정확히 해를 구할 수 있게 됩니다.

Code of KL-Divergence

출처 : https://github.com/hwalsuklee/tensorflow-mnist-VAE/blob/master/vae.py

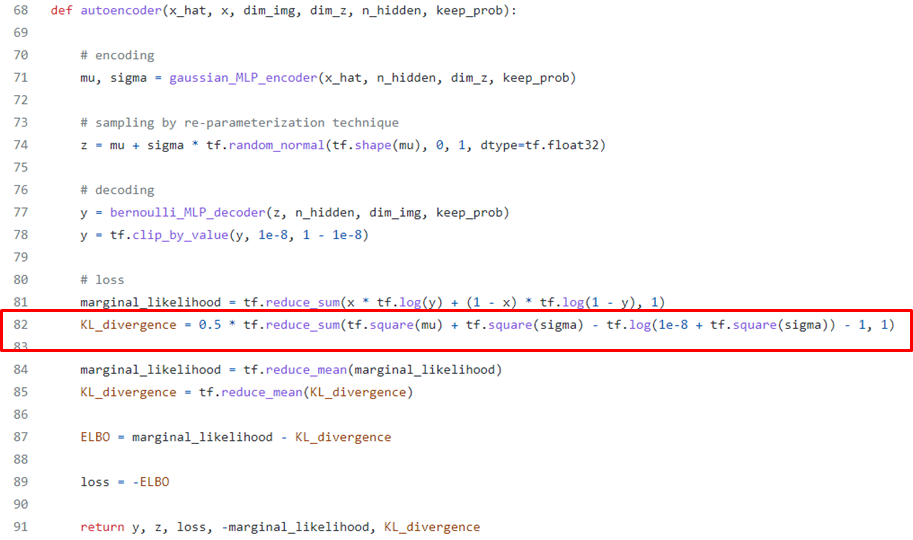
Reconstuction Error term

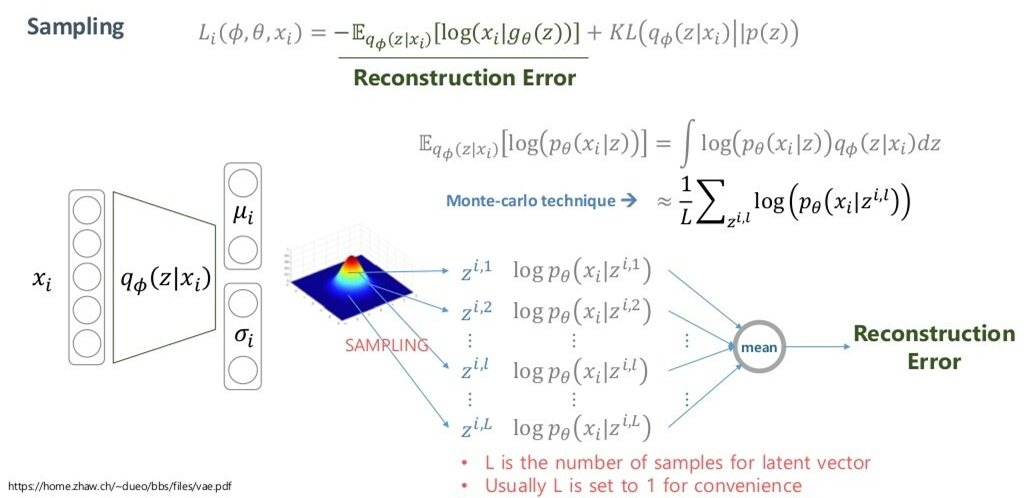
이 때, sampling을 진행해서 $z$를 사용하는데, 문제는 샘플링 함수는 random function이기 때문에 일반적으로 역전파를 진행할 수 없다는 것입니다. 저희는 $z$가 도출되는 $\mu, \sigma$를 학습시켜야 하기 때문에 역전파는 구해야 합니다.

---

re-parameterization trick

그래서, 우리는 re-parameterization trick을 사용해 아래와 같이 식을 변경해줍니다.

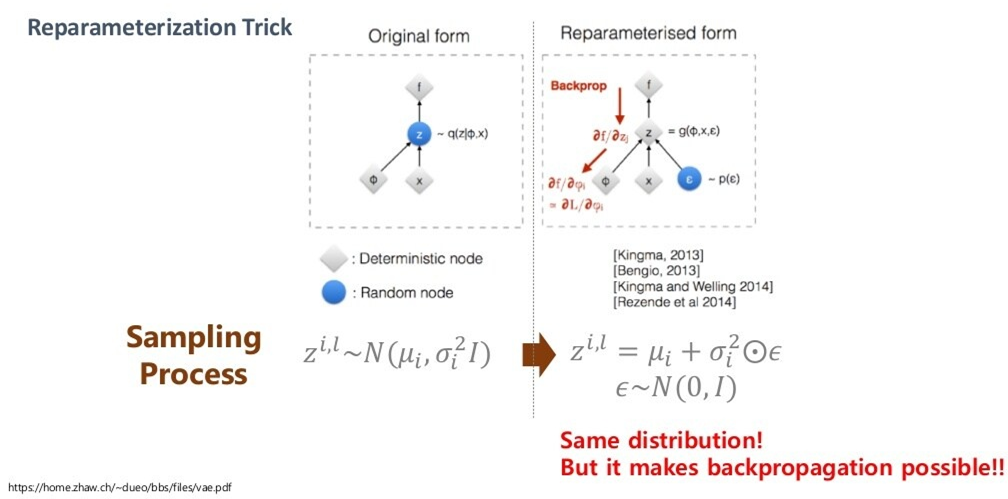
우측의 식으로 변형하더라도 분포는 변하지 않기 때문에 위와 같이 변형을 할 수 있는 것이고, 이로부터 $\mu, \sigma$에 대한 그래디언트를 구할 수 있게 됩니다.

Code of re-parameterization trick

출처 : https://github.com/hwalsuklee/tensorflow-mnist-VAE/blob/master/vae.py

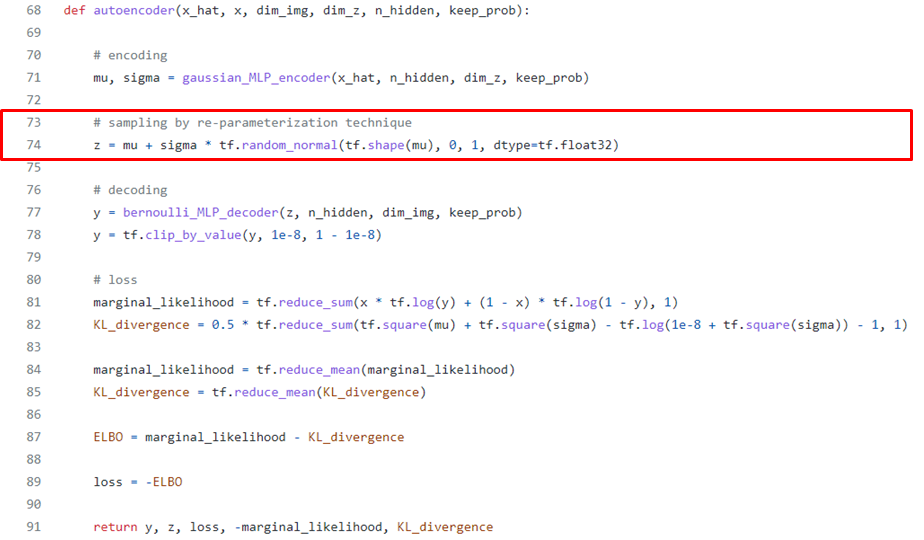
단, tf.random_normal method 내에 이미 re-parameterization trick이 적용되어 있기 때문에 실질적으로 mu와 sigma를 인자에 넣고 $z$를 단순히 샘플링해도 문제는 없습니다.

---

Bernoulli Decoder vs Gaussian Decoder

Bernoulli Decoder

또한, 원래 샘플링을 통한 몬테카를로 방법을 적용해야 하지만 일반적으로 샘플링도 단 한번만 적용해 사용한다고 합니다.

King.Ma, Auto-Encoding Variational Bayes (4p 중 발췌)

위의 예시처럼 generator의 likelihood $p_{\theta}(x|z)$가 베르누이분포를 따른다고 가정했을 때, 최종적인 likelihood는 network의 input $x$와 network의 output $p$의 Cross-entropy가 됩니다.

---

네트워크의 출력이 베르누이 분포의 출력인 0 or 1이 되는 것이 아닙니다. 네트워크의 입력 $x$ 또한 무조건적으로 베르누이 분포를 따라 $x\in \{0,1\}$의 값을 갖는 것이 아닙니다. 단지 그냥 합리적(경험적) 가정일 뿐이며, $p_{\theta}(x|z)$은 확률적인 관점에서 $p^{x}(1-p)^{1-x}$의 값(즉, 0과 1 사이의 값)을 output으로 가집니다. 또한 최종적인 Cross entropy에서도 굳이 label이 0과 1만을 가질 필요는 없습니다.
Cross entropy의 대표적인 사용처인 Classification에서는 label이 one-hot encoding으로 0과 1의 값만 가지는 것은 그저 극단적인 정답의 예시(hard)일 뿐, 0과 1사이의 값을 가져도 cross entropy를 사용할 수 있습니다(softmax).
!()

---

Gaussian Decoder

만약 likelihood $p_{\theta}(x|z)$가 가우시안분포를 따른다고 가정한다면?
즉, $z$를 조건으로 받은 generator의 output이 평균 $\mu$와 분산 $\sigma$를 따른다면?

위와같이 최종적인 likelihood $p_{\theta}(x|z)$는 input $x$와 output $\mu$(를 따르는 샘플) 간의 MSE loss가 됩니다.

특히, 분산을 0으로 했을 때에 완벽한 MSE loss가 됩니다.
위에서 평균과 분산은 element-wise 될 것이기 때문에 그냥 $D$ 차원의 vector가 하나 생긴다고 보면 됩니다.
또한, 학습이 잘 됐다면 $z$를 $q_{\phi}(z|x)$에서 샘플링했음에도 불구하고, 이상적인 $p(z|x)$와 굉장히 유사해질 것이고, 그에 따라 나온 $z$를 토대로 generator $q_{\theta}(x|z)$ 또한 최적화된 것이기 때문에 생성 성능이 좋습니다.

---

Bernoulli Decoder

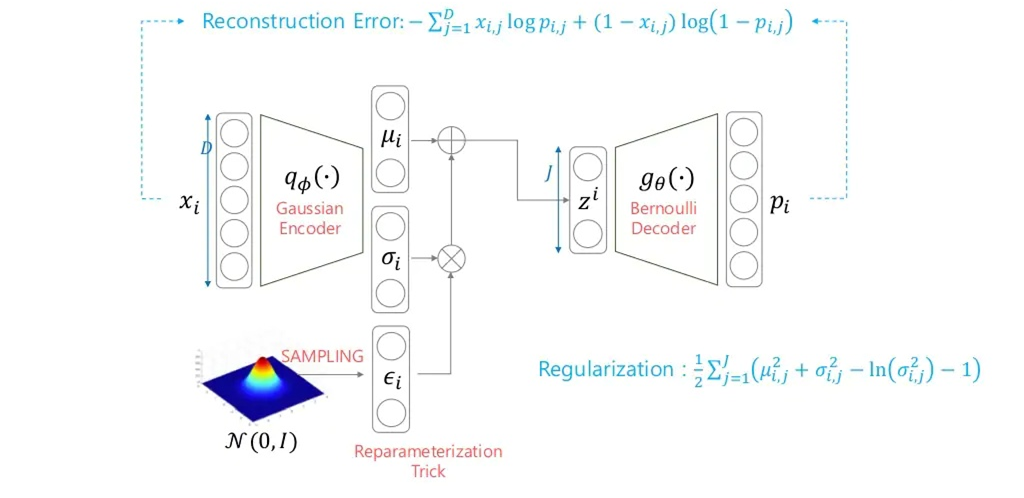
그래서, 한 장으로 요약하면 결국 Reconstruction Error는 (디코더의 likelihood를 베르누이로 가정했기에) input과 ouptut의 Cross-entropy term으로 바뀌며, Regularization Error는 (사전분포와 Approximation class를 가우시안분포로 가정했기에) closed form으로 계산할 수 있게 됩니다.

Gaussian Decoder

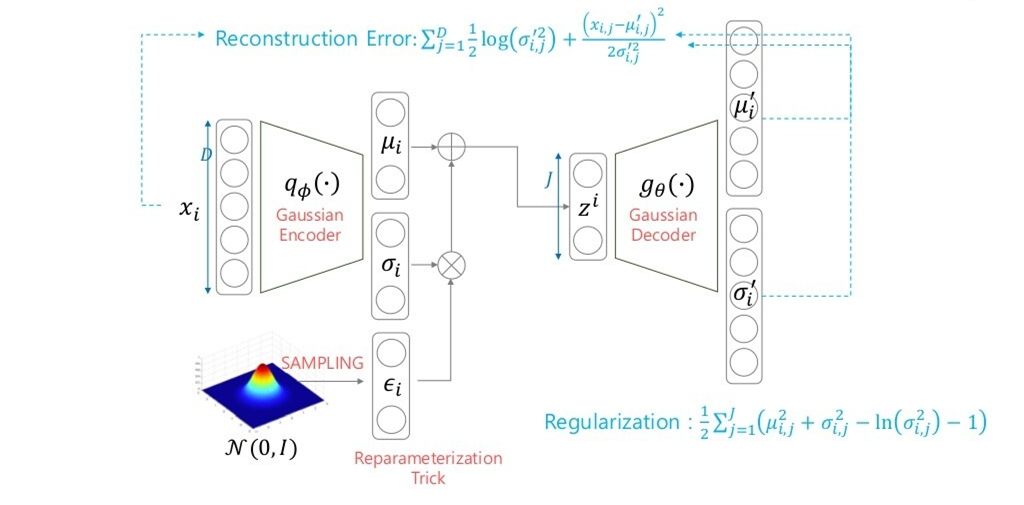
• 마찬가지로, 위와 같이 표현할 수 있습니다.

만약 위에서 분산 $\sigma$가 1이 아니라면, 분산이 커질수록 Reconstruction Error, 즉 observations(data)의 영향력은 작아지고, Regularization Error, 즉 prior의 영향력은 강해집니다. 즉, 기본적으로 베이지안 추론의 관점(data+prior -> posterior)에서 data와 prior간의 trade-off를 control하는 term이 $\sigma$의 역할이라고 해석할 수도 있습니다.

Decoder의 분포에 변화를 주는 것과 다르게 Encoder의 분포는 고정시키는데, 이는 정규분포가 아닌 경우 KL-발산 term을 구하기가 쉽지 않기 때문입니다. 이러한 한계에 대해 해결한 것이 Adversarial Auto Encoder입니다.

Result

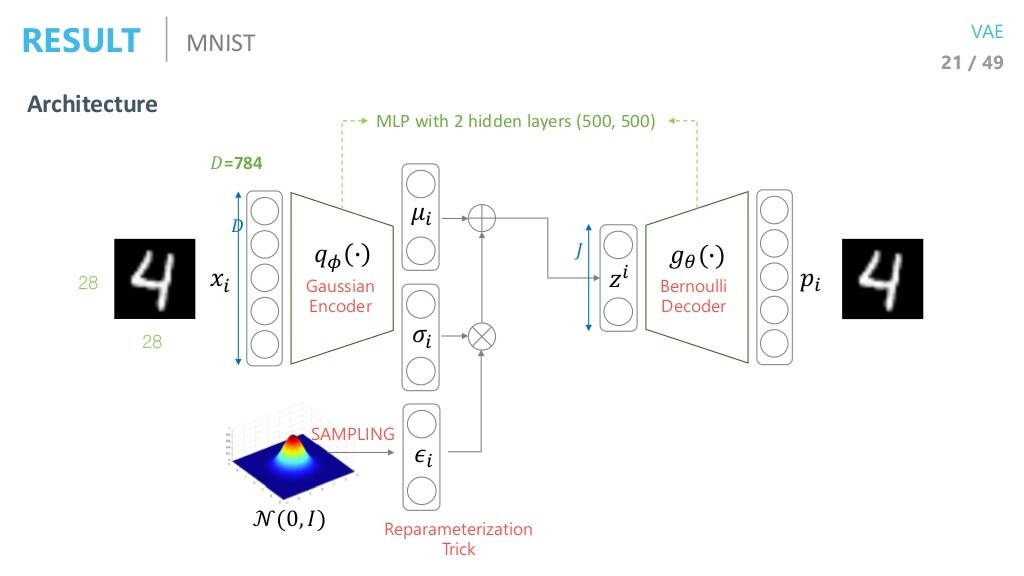
Architecture

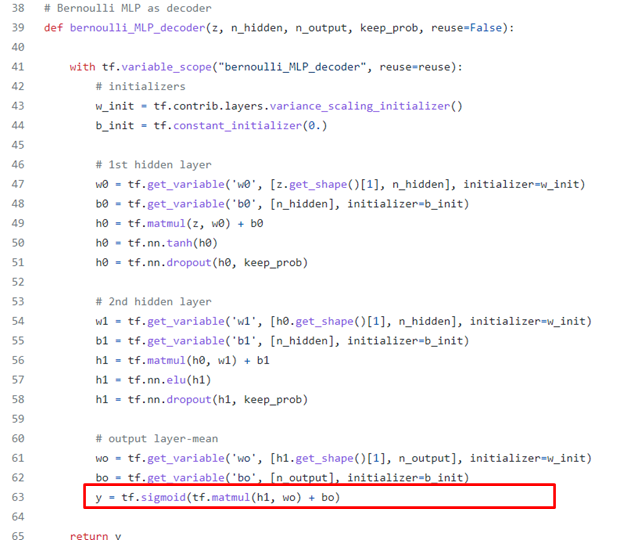
Code(Bernoulli Decoder)

출처 : https://github.com/hwalsuklee/tensorflow-mnist-VAE/blob/master/vae.py

위의 코드에서 평균과 분산을 따로 나눠서 결과로 내는 것을 볼 수 있습니다. 이는 두 parameter를 각각 추정해야하기 때문이며, 최종적인 sample의 값은 element-wise됩니다. n_output은 추정할 잠재벡터 $z$의 차원입니다. 즉, 최종적으로 반환되는 평균과 분산은 모두 n_output 차원을 갖습니다.

Encoder

Decoder

Decoder 또한 비슷하지만, output이 보통 image기 때문에 최종 활성화 함수는 sigmoid를 사용해 0~1사이의 값으로 맞추어줍니다.

VAE

• 전체 코드는 간단합니다.

Result

• input image의 차원($784=28\times28$)을 $2, 5, 20$차원으로 줄였을 때의 결과입니다. 당연히, 잠재벡터의 차원이 높을수록 복원이 잘 될 것이기에 Reconstruction Error는 더 줄어듭니다.

AutoEncoder vs VAE

근본적으로 AutoEncoder의 loss와 VAE의 loss는 KL-발산 term을 제외하면 모두 같습니다.

AutoEncoder는 VAE와 구조, 그리고 Reconstruction Error가 사실상 같습니다. 하지만, AutoEncoder에서는 Decoder(Generator)의 관점에서 잠재벡터 $z$에 대한 고려를 하지 않습니다. 즉, $z$가 어떤 range에 놓여야 이상적으로 generation을 하는 지는 모르고, 그저 복원 성능만을 신경씁니다.
반면, VAE에서는 학습이 잘 됐다면 $z$를 $q_{\phi}(z|x)$에서 샘플링했음에도 불구하고, 이상적인 $prior$(정규분포)와 굉장히 유사해질 것이고, 그에 따라 나온 $z$를 토대로 generator $p_{\theta}(x|z)$ 또한 최적화됩니다.

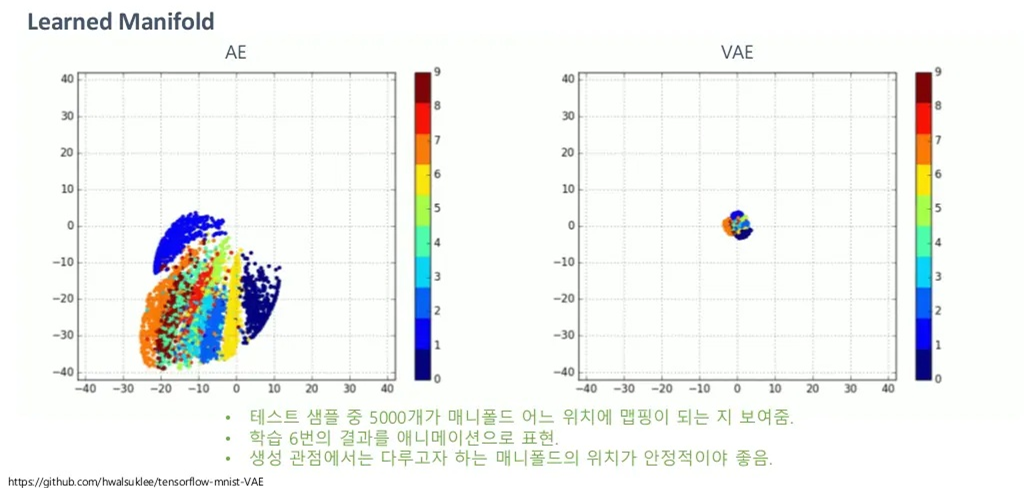
결론적으로, AutoEncoder는 학습을 새로 할 때마다 $z$의 분포가 매우 달라지고, 난장판이 되는 반면 VAE는 학습을 새로 하더라도 $z$가 안정적으로 정규분포를 따르기 때문에 추후에 샘플을 생성할 때에도 그저 학습된 $z$의 prior 분포(즉, 정규분포)로부터 $z$를 뽑아서 생성하면 됩니다. 훨씬 더 편하게, 그리고 유의미하게 잠재벡터를 다룰 수 있는 것입니다.

우리의 $ELBO$ loss는 (가정상 정규)사전분포 $p(z)$와 샘플링함수 $q_{\phi}(z|x)$가 가까워지게끔 학습을 시켜줍니다.

이러한 VAE의 특성으로 인해 잠재벡터 $z$는 아래와같이 자동적으로 유의미한 특성을 지니게끔 학습되고, 정규분포를 따릅니다.

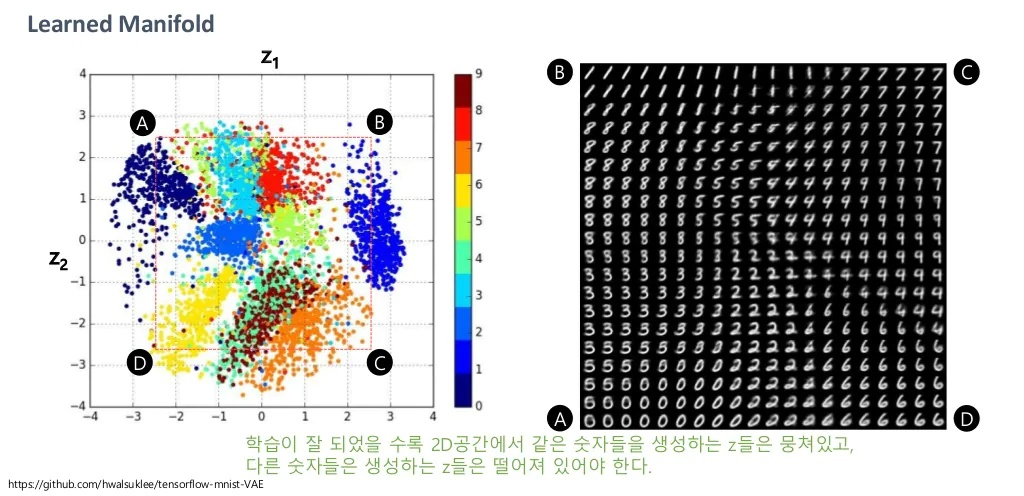
물론 위의 예시에서는 균등분포에서 샘플링을 했지만, 정규분포에 따라 샘플링을 한다면 클래스 별 빈도정도는 다를 수 있을 것입니다.

E.T.C.

1. MNIST VAE에서 베르누이 분포를 가정하고 BCE loss를 사용하는 이유

https://arxiv.org/pdf/1606.05908.pdf

Although MNIST is real-valued,

• 사실 MNIST는 real-value(continuous)에 가깝기 때문에 가우시안 분포로 가정하고 진행하는 게 이론적으로는 옳습니다.

  픽셀 값 0,1,2,...,255를 Class로 정의해서 Categorical cross entropy를 적용할 수는 없지 않은가..?

• 하지만, 경험적으로는 성능이 베르누이 분포일 때 더 잘나온다고 하니.. (위 출처에 관련 내용 있습니다).

1.1. 또한, 굳이 BCE loss가 0과 1의 값만 다룰 필요는 없다.

• 물론 이론적으로 베르누이 분포는 0과 1의 값만 갖는 게 맞지만, 엄연히 정해진 parameter에 따라 0과 1이 정해지기 때문입니다.

이에 대해서는 TFKR, facebook
를 참고하면 이해하기 좋습니다.

---

2. negative log likelihood를 사용하는 이유

i.i.d 조건으로부터 아래의 Assumption을 도출해낼 수 있게 된다.

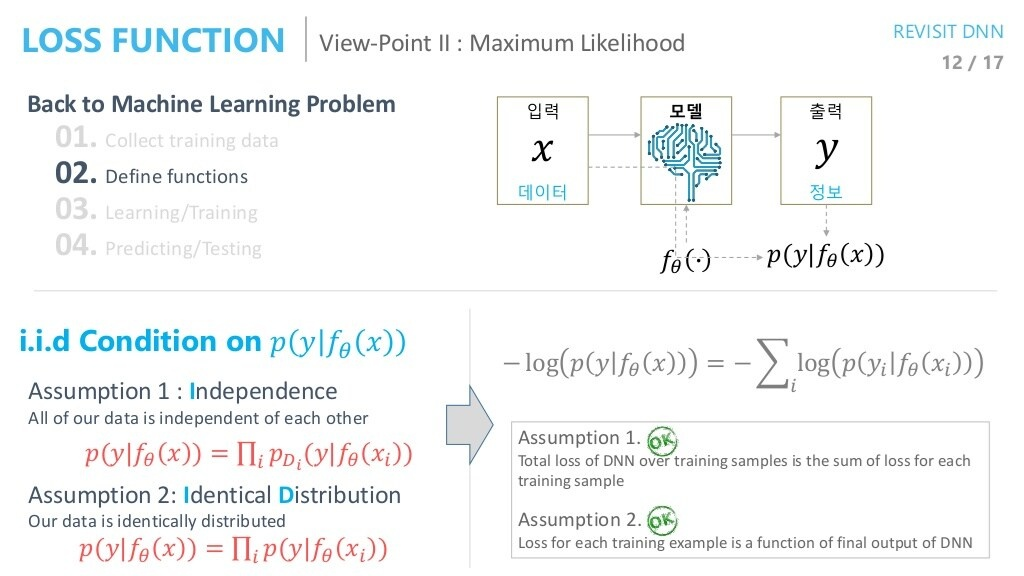
• 또한, MSE LOSS와 CROSS ENTROPY LOSS가 위 조건을 만족시키는 대표적인 식입니다.
• 또한, loss는 pixel 간에 계산되고, 합해지는 모양 새를 가지니 헷갈리지 않도록 합시다.

2.1 MSE and cross entropy

위 내용에 대한 개략적인 이해는 https://simpling.tistory.com/15를 참고하세요.

---

3. Cross-entropy for comparing images

https://stats.stackexchange.com/questions/349096/cross-entropy-for-comparing-images

4. softmax가 soft인이유는?

보통 0~1사이의 값을 갖는 확률분포를 반환할 때 softmax를 사용한다. 만약 그 확률분포에서 가장 높은 확률을 갖는 위치에 1을 할당하고, 나머지 위치에 0을 할당한다면 one-hot prediction을 반환하게 된다.
즉, 여기서 one-hot vector가 hard, softmax vector가 soft라고 봤을 때, softmax의 vector 전체를 아우르는 성격덕분에 전체 위치(학습 시 클래스)에 대한 학습을 진행할 수 있게 되는 것이다.

5. Deterministic function?

https://stats.stackexchange.com/questions/347378/variational-autoencoder-why-reconstruction-term-is-same-to-square-loss

6. AutoEncoder의 응용방법?

AutoEncoder와 관련해 Feature를 잘 압축하는 방법 중 하나는, 우선 특정한 fixed-length vector로 압축을 해본 다음,그것을 한번 더 고전적인 차원축소 방법으로 한번 더 차원 축소를 진행해 Visualization을 해보는 것입니다. 왜냐면, T-SNE같은 차원축소 방법론들은 이웃 간 관계가 잘 유지되는 특성을 지니며, AutoEncoder 또한 매니폴드 상에서 이웃 간의 관계가 잘 정립되기를 원하므로, 만약 AutoEncoder를 통해 특정한 fixed-length의 vector로 잘 압축이 됐다면, 고전적인 차원축소 방법들로 추가적으로 차원을 축소해 시각화를 했을 때에도 성능이 좋을 것이라는 가정을 할 수 있기 때문입니다.