norm의 정의

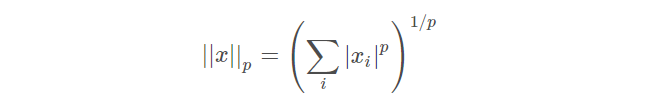
L1 norm

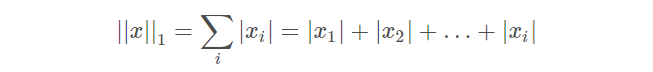
L2 norm

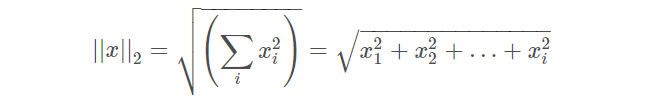
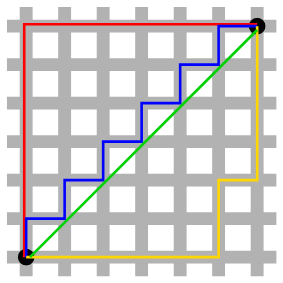
L1 norm(red, blue, yellow), L2 norm(green)

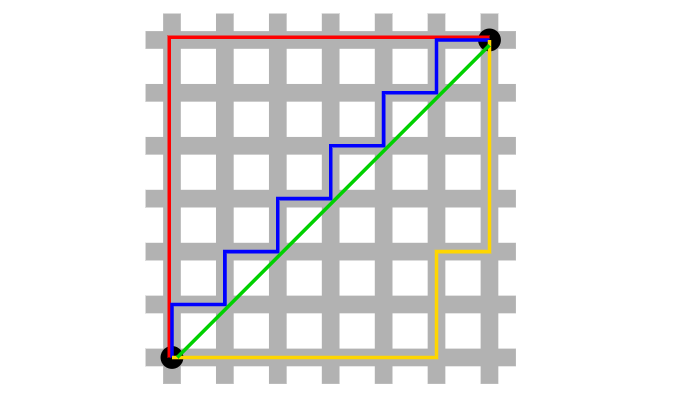
L1-L2 norm comparisons

Robustness: L1 > L2

• Robustness : 데이터 셋에서 이상치(outliers)에 대항하는 능력

가령, pixel이 $[1,1,1,1,10]$을 가진다 가정해봅시다(비교 대상은 원점).
이 때 이상치는 $10$이 됩니다.

L1 norm을 가정하면 $1+1+1+1+10=14$가 나오고,
L2 norm을 가정하면 $1+1+1+1+100=104$가 나옵니다.

이럴 때 $1$의 픽셀 값은 어떤 곳에서 더 의미가 있을까요?
단순하게 생각했을 때 L1 norm을 평균내면 $2.8$, L2 norm을 평균내면 $20.8$이 됩니다.

이럴 때 $1$의 값을 가지는 픽셀은 L2 norm에서는 사실상 의미가 없어지겠죠(1 <<<<<<< 20.8 $) 반대로 $1의 값을 가지는 픽셀은 L1 norm에서 나름의 역할을 할 수 있습니다($1 < 2.8$).

즉, $L2 norm$은 사실상 이상치 $10$에 의해서만 최종 norm이 결정되므로 나머지 픽셀 값들은 무시된다 할 수 있고, 그렇기 때문에 L2 norm이 이미지 간 비교에 적용된다면 픽셀들은 blurry한 성질이 생기기도 합니다.

Stability: L2 > L1

in Wikipedia
The instability property of the method of least absolute deviations means that, for a small horizontal adjustment of a datum, the regression line may jump a large amount. The method has continuous solutions for some data configurations; however, by moving a datum a small amount, one could “jump past” a configuration which has multiple solutions that span a region. After passing this region of solutions, the least absolute deviations line has a slope that may differ greatly from that of the previous line. In contrast, the least squares solutions is stable in that, for any small adjustment of a data point, the regression line will always move only slightly; that is, the regression parameters are continuous functions of the data.

• Stability : 수평 조절에 저항하는 능력

horizontal adjustments를 표현하는 좋은 그림은 아래와 같습니다.

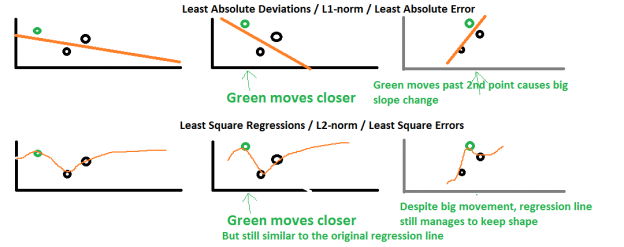
• L1 norm : 데이터가 변하면 직선(L1 norm)도 심하게 변한다.
• L2 norm : 데이터가 변하면 곡선(L2 norm)은 별로 변하지 않는다.

출처 : http://www.chioka.in/differences-between-the-l1-norm-and-the-l2-norm-least-absolute-deviations-and-least-squares/

Solution 개수: L2 <<<<< L1

아래 그림만 봐도 L1 norm을 기술하는 방법은 굉장히 많습니다.

L1-L2 regularizer comparisons

Computational difficulty: L1 > L2

• L2 norm : 제곱 합이므로 해가 closed form으로 존재한다.
• L1 norm : 절대 값을 포함하므로 not closed.

이런 이유로, L1 norm이 연산하기가 훨씬 어렵습니다. matrix form으로 계산할 수 없으니까요.

그렇기 때문에 approximations에 의존하는 경향이 있습니다(마치 lasso에서 coordinate descent를 사용하는 것처럼).

L2 norm처럼 곧바로 구할 수 있는 해를 analytical solution이라 하기도 합니다.

Sparsity : L1 > L2 for Feature Selection

• Sparsity : 매우 중요한 coefficients를 가지는 특성

즉, 대부분 0이지만 *매우 소수의 계수만이 0이 아니라면** Sparsity가 강하다 말할 수 있습니다.

예를 들어, one hot vector !

그래서, Feature Selection이 Sparsity와 큰 관련이 있습니다.

거의 0에 가까운 특성들은 그냥 제거를 해버리고 남은 것만 쓰는거죠.

주의 : 단순한 L1 norm과 L2 norm을 비교하는 게 아닌, Regularization으로서의 역할을 비교한 것입니다 !

가령, $||Y-WX||_1$와 $||Y-WX||_2$를 비교하는 게 아닙니다.
이렇게 비교한다면 오히려 제곱을 하는 $||Y-WX||_2$가 sparse한 성질을 가지겠죠.

즉,
기존의 least-squares(L2-norm cost function)가 아래와 같을 때
$(Y-WX)^{2}$
L1 regularization과 L2 regularization은 아래와 같습니다.
$(Y-WX)^2+|W|$
$(Y-WX)^2+W^{2}$

이 경우 모델의 $W$를 sparse하게 만드는 것은 L1 regularization term인 $|W|$입니다.

L2 regularization term인 $W^{2}$은 특정 값이 너무 커지는 것을 방지해줍니다. 이상치(outlier)의 영향력이 너무나도 세기 때문에 (Regularization) cost가 높아지면 자동적으로 이상치를 낮추는 쪽으로 feedback을 주게 됩니다.

하지만, L1 regularization term인 $|W|$은 이상치에 대한 영향이 굉장히 작습니다. 즉, (Regularization) cost $|W|$는 어차피 이상치가 크든 말든 상관이 없습니다.
그렇다는건, 기존의 L2 loss $(Y-WX)^{2}$만 높으면 장땡이기 때문에 $W$의 계수(coefficient)는 이상치를 가지게 되며, Sparse해지며, 그로 인해 Feature selection에도 사용할 수 있게 되는 것입니다.

예시

$W$ = [10,1,1,1,1,1] 이라 가정합시다.

그러면, 여기서 original loss $(Y-WX)^2$가 도출될 것이고, 이 값을 $k$라고 해봅시다.

그러면, L1 regularization loss과 L2 regularization loss을 적용했을 때 final loss는 아래와 같이 주어집니다.

• $L1$ : $(Y-WX)^2+|W|$ = $k$ + 15
• $L2$ : $(Y-WX)^2+W^{2}$ = $k$ + 105

어떤가요? $L2$ regularization은 이상치 10이 Reg-loss 105에 대부분 관여하고 있습니다($100/105:95.2$는 비교적 골고루 분포하게 됩니다.

반면, $L1$ regularization은 이상치 10이 Reg-loss 15에 영향을 끼치긴 하나 비교적 영향력이 적습니다($10/15=66.6$). 그렇다는 건, original loss $(Y-WX)^2$만 충분히 작다면, 이상치 10이 있든 말든 Reg-loss는 과하게 규제를 가하지 않게 되고, 최종적인 Weight $W^{*}$는 이상치가 과하게 개입된, Sparse한 weight가 되는 것입니다.

다만, 위에서 단순히 수치 15와 105를 비교하는 것은 당연히 옳지 않습니다 !
당연히 제곱해주는 L2 norm이 값 자체는 큽니다(편의상 root는 제외하므로).

---

Ref
https://www.kaggle.com/residentmario/l1-norms-versus-l2-norms
http://www.chioka.in/differences-between-the-l1-norm-and-the-l2-norm-least-absolute-deviations-and-least-squares/