1. Introduction to Lauguage Modeling

우선, Language Modeling의 가장 큰 목표는 아래와 같다.

문장에 대한 확률을 할당하자

NLP의 응용분야들을 생각했을 때, 이러한 목표는 당연하게 여겨진다.

가령, 기계번역 분야에서는 더 나은 번역 결과를 위해 여러 문장을 비교해야 할 때가 있다.

영어 : The car is fast

한글 1 : 그 자동차는 빠르다
한글 2 : 그 자동차는 단식중이다.

위의 결과로 봤을 때,
한글 2보다는 한글 1이 더 그럴싸한 문장이고, 이를 $P(한글1;영어)>P(한글2;영어)$와 같이 확률문제로 나타내 처리할 수 있기 때문이다.

번역이 아니더라도 수 많은 응용 분야(Q&A, Summarization, etc)에서도 단어의 확률, 문장의 확률 등의 문제로 치환시켜 풀 수 있다.

즉, 언어 모델링의 목표는 문장의 확률을 구하거나 혹은 단어 시퀀스의 확률을 구하는 것이라 할 수 있다.

문장의 확률을 나타내는 결합 분포 $P(W)=P(w_1,w_2,...,w_n)$와 이전 단어가 주어졌을 때 다음 단어의 확률을 나타내는 조건부 분포 $P(w_n|w_1,w_2,...,w_{n-1})$는 굉장히 유사하기 때문에(후자를 재귀적으로 곱해준다면) 이 두 개를 모두 Language model이라 한다.

---

How to compute P(W)

적당히 연쇄 법칙(Chain Rule)을 써서 조건부확률의 곱으로 나타낼 수 있다.

위와 같은 과정을 아래의 기호로 표현할 수 있다.

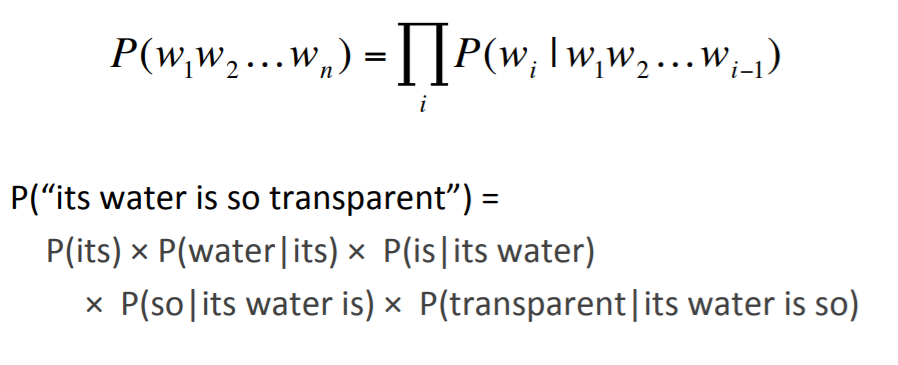
자, 그러면 결론적으로 위에 나타난 확률 $P$는 어떤 식으로 계산할 수 있을까?

가장 간단하게는, 확률의 정의를 이용할 수 있을 것이다.

• A 문장의 확률 = (A 문장의 발생 횟수)/(전체 가능한 문장의 경우의 수) - Counting??
  

당연히, 계산할 수는 없다.

애초에 가능한 문장의 경우의 수는 너무나 많을 뿐더러, 그에 비해 특정 문장의 발생 횟수는 너무나도 작다.

그렇기 때문에, Markov Assumption을 이용해 확률을 계산할 수 있다.

Markov Assumption

즉, (조건부)확률을 문장 단위로 다루기 어렵기 때문에 이전 '한 단어' 혹은 '두 단어'만을 다루는 것이다.

더 일반적으로, 이전의 모든 단어를 고려하지 않고, 이전 k개의 단어만을 고려했을 때, 다음 단어가 나올 확률을 나타내는 언어 모델링을 아래와 같이 표현할 수 있다.

N-gram

Uni-gram(이전 0개의 단어)

위와 같이 마르코프 가정에서 나온 개념을 흔히 gram을 사용할 수 있고, 이전 단어의 맥락을 사용하지 않는 것을 Unigram(다음에 나오게 될 관심 단어를 포함해서 1개), 이전 1개의 단어만을 사용하는 것을 Bi-gram(이전 1개의 단어 + 다음에 나오게 될 관심 단어 1개), 이전 N-1개의 단어만을 사용하는 것을 N-gram이라 할 수 있다.

이 중 Uni-gram이 특이한데, 이전 맥락을 보지 않기 때문에 전체 문장은 완전히 랜덤한 단어들의 나열로 형성될 것이다.

Bi-gram(이전 1개의 단어)

그래도 어느 정도 영어 문장으로 볼 수는 있다(의미적으로는 거의 무의미하지만).

N-gram(이전 N-1개의 단어)

• 어느 정도 이전 맥락이 길어질수록 문장 확률의 모델링은 잘 되겠지만, 연산량이 기하급수적으로 증가하며, 언어의 Long-term Depende ncy(장기 의존성)을 고려했을 때 꽤나 큰 $N$이 필요할 것이기에 N-gram도 마냥 좋은 언어 모델링은 아니라 할 수 있다.

가령,
그 남자는 공을 차서 학교 유리창을 깼기 때문에, 학교 선생님은 ( )를 불러서 혼냈다.
라는 문장이 있을 때 ( ) 안에 들어갈 단어는 그 남자일 것이다.
다만, 이를 알기 위해서 최소한 10개 가량의 이전 맥락을 봐야하며, 가능한 단어의 규모를 생각했을 때 너무나 많은 경우의 수가 생긴다.

단어가 30000만개라면, 이론적으로 $30000^(10)$개의 경우의 수.

즉, Long-distance dependencies, 즉 장기 정보를 다루기 위해서는 N-gram보다 좋은 모델이 필요하다는 것을 암시한다.

다들 알다시피 이는 RNN, LSTM, GRU 계열의 딥러닝을 통해서 엄청난 발전을 이루었다.

2. Estimating N-gram Probability

Bi-gram estimating

계산을 해봅시다.

우선, Bi-gram을 예시로 계산하면, 아래와 같이 확률을 계산할 수 있습니다.

• $c\approx count$

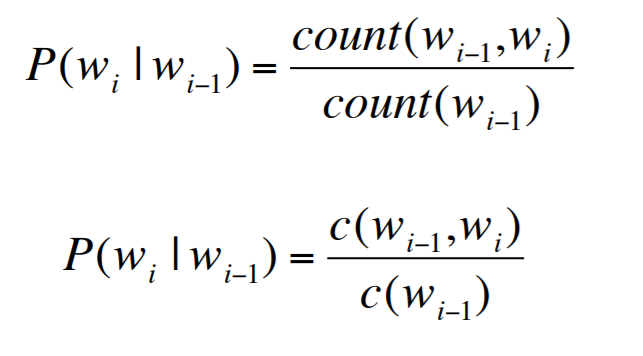
굳이 따지자면 Maximum Likelihood Estimator를 이용해 가장 높은 확률을 보이는 단어를 선택하는 것입니다.

영어 문장을 예시로 살펴봅시다.

$<s>$와 $</s>$는 각각 문장의 시작, 끝을 알리는 토큰입니다.

• I am SAM
• Sam I am
• I do not like green eggs and ham

즉, 위의 세 가지 문장을 corpus로 생각하고, 각각의 Bi-gram 확률을 계산하면 아래와 같이 계산할 수 있습니다.

이전 사진을 참고로 계산하면 아주 쉽다.

다른 레스토랑-related corpus를 이용하면 아래와 같이 bigram count을 계산할 수 있습니다.

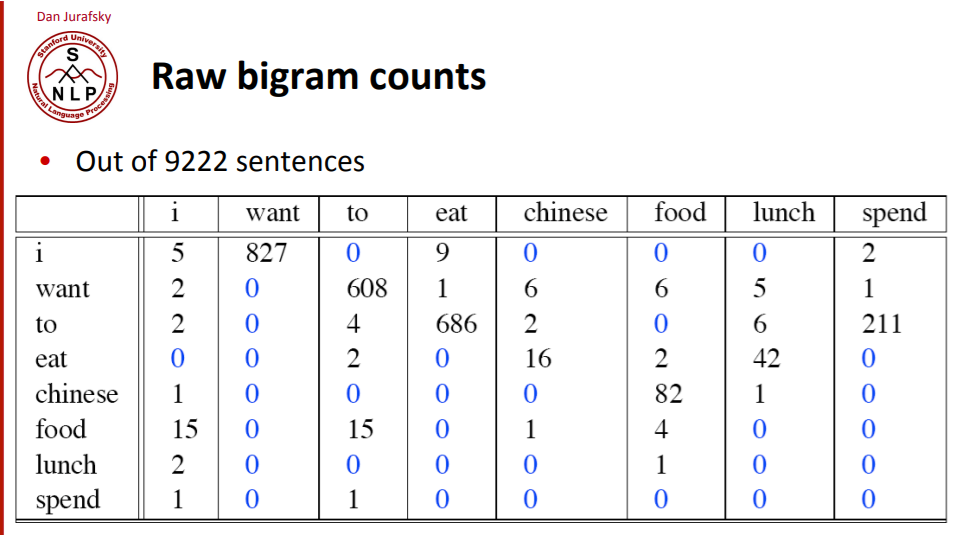
위에서 나타난 bi-gram count를 확률로 바꾸기 위해서는 uni-gram count로 normalize하는 것처럼 생각할 수 있습니다.

$p(w_i|w_{i-1})=c(w_{i-1},w_i)/c(w_{i-1})$
에서, 분모가 unigrame count이므로.

그러면, 아래와 같이 확률표를 도출할 수 있다.

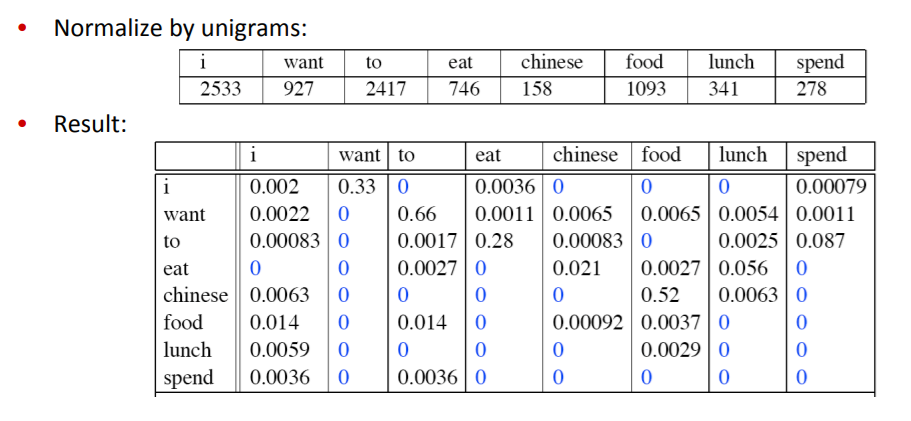
이와 같은 요소들을 이용하면 결국 재귀적으로 조건부확률을 곱해나가 문장의 확률을 구할 수 있게 됩니다(bi-gram).

그러면, 이처럼 bigram으로 모델링을 할 경우 어떤 정보를 얻을 수 있을까요?

• english food가 chinese food보다 인기가 없다(세상사).
• want는 to 부정사를 필요로 한다(문법).
• want와 spend, 즉 동사 두 개는 연속적으로 쓸 수 없다(문법, 진리).
• to 다음에 food가 올 수 없다(?)(이건 학습 데이터에만 없는, 우발적인 상황일 뿐, to 다음에는 food가 올 수도 있다).

Practical Issues

Log probability

보통 곱셈보단 덧셈이 여러 연산에 유리한 편입니다(add is faster than multiple).
뿐만 아니라 곱셈을 할 경우 값 자체가 굉장히 작아질 수도 있구요(Underflow).

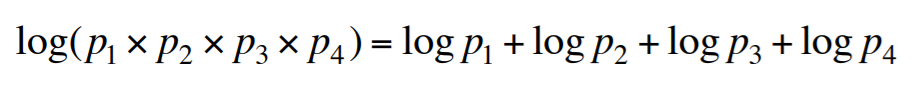
딥러닝에서 소프트맥스를 구할 때 $exponential$을 취하지 않고 log로 돌리는 이유와 유사합니다(overflow 방지).

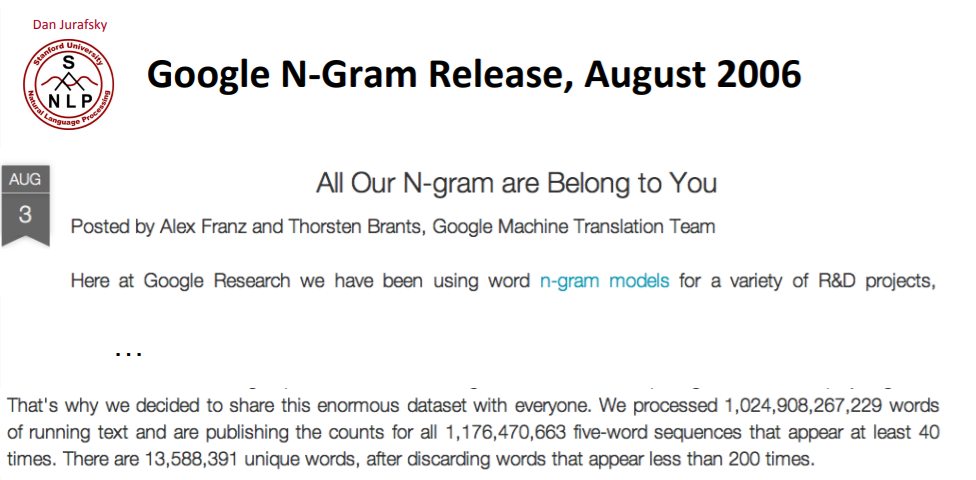
여러 n-gram dataset이 존재한다.

3. Evaluation Perplexity

모든 랭귀지 모델들은 특정한 기준을 사용해 평가를 진행해야 어떤 모델이 좋은 모델인지 판단할 수 있습니다.

대략적인 기준은 아래와 같습니다.

1. 실제 문장(or 그럴듯한 문장)이 나올 확률을 높힌다.
2. 문법적으로 불가능하거나 좀처럼 나오지 않는 문장은 줄인다.

• training set을 이용해 *parameter를 평가해야 합니다.
• 한 번도 보지 못한 test set(unseen data)를 사용해 평가해야 합니다.

Extrinsic evaluation

두 랭귀지 모델을 비교하는 가장 좋은 방법은 오탈자 고치기, 기계번역, 스피치 인식 등 여러 task에 대해 직접 예측을 수행하고, 이로부터 accuracy를 얻어 비교하는 것입니다.

• 즉, task에 따라 accuracy를 얻는 방식은 다를 수 있습니다(문자 단위로 error를 구할 수도, 단어 단위로 error를 구할 수도, 문장 단위로 error를 구할 수도 있습니다).

이런 방식을 Extrinsic evaluation이라 합니다.

N-gram 그 자체를 평가하는 게 아니라 외부(externel) task를 이용해서 간접적으로 평가하므로.

• in-vivo evaluation으로 불리는 외부 평가 방식은 시간이 꽤나 들 수 있습니다.

Intrinsic

그래서, 랭귀지 모델을 그 자체로 평가하는 Intrinsic evaluation을 진행하기도 하며, 대표적으로는 Perplexity가 있습니다.

물론, 학습 데이터에서 자주 보지 못한 데이터에 대해서는 좋지 못한 결과를 보여 extrinsic evaluation을 같이 활용해야 합니다만..

Intuition of Perplexity

랭귀지 모델링의 많은 아이디어가 정보이론의 대가 샤넌으로부터 나왔습니다.
그 중 대표적으로 샤넌 게임(Shannon Game),즉,
다음으로 어떤 단어가 올까?
라는 것이 있습니다.

즉, 아래와 같이 다음으로 올 단어들의 확률 분포를 생각해볼 수 있습니다.

이 때, 좋은 랭귀지 모델은 실제로 다음에 나타날만한 단어들에 높은 확률을 부여하는 모델이라 할 수 있습니다.
뿐만 unseen data에도 좋고, 높은 확률 분포를 예측해주면 더욱 좋겠죠.

아무튼, 이런 확률에 대한 관점으로 본다면, 실제 문장의 확률이 높을수록 좋은 랭귀지 모델이고, Perplexity를 확률의 역수로 정의함으로써 Perplexity를 낮추는 방향으로 모델링을 진행할 수 있습니다.

문장이 길어질수록 확률은 낮아질 수밖에 없기 때문에 길이에 대한 term을 정규화시켜주기 위한 n-th root가 존재합니다.

---

다른 방식으로도 생각해볼 수 있습니다.

Josh Goodman으로부터 나온 Perplexity는 일종의 average related to the average branching factor라 할 수 있습니다.

가능한 분기점들에 대한 평균..?

즉, 문장의 특정 지점에서의 Perplexity는 평균적으로, 얼마나 많은 단어들이 다음에 올지에 따라 결정됩니다.

이는 엔트로피 개념과도 유사한데, 가령 단어 뒤에 특정한 숫자가 오는 것을 예측한다면, 가능한 숫자는 0~9 총 10가지이고, 숫자 간에는 일반적으로 우선순위를 가르기 힘들기 때문에 모두 10%로 같은 확률을 지니고, 따라서 Perplexity는 10입니다.

다만, '인간의 눈은 일반적으로 ( )개이다' 라는 문장 내에서, ( )에 들어올 숫자는 2이고, 만일 랭귀지 모델이 2에 대한 확률을 99.999999%로 반환한다면, 이는 0에 가까운 Perplexity를 반환하겠죠.

즉, 예측한 단어의 개수와는 별개로, 확률을 어떻게 부여하는 지에 따라서 가중치를 부여한, Weighted equivalant branching factor**라 할 수 있습니다.

평균적으로 하나의 단어는 어떤 확률로 발생할까.

• 이런 branching factor를 이용한 Perplexity가 왜 역수&정규화로 정의한 Perplexity와 같은지 알아봅시다.
  

예시로 $N$개의 random digit을 예측하는 sentence를 생각해봅시다.

즉, 위에서도 보다시피 Perplexity를 inversed noramlized probability로 생각하는 것을, 직관적으로, 얼마나 많은 단어들이 나타날 지를 각각의 확률에 따라 가중, 길이에 따라 정규화한 것으로 생각할 수 있습니다.

수식적으로 바라보기 보다는, 그냥 직관적으로 다음에 오게될 단어들이 많을수록 Perplexity가 높다고 생각하면 됩니다.

---

당연히 모델이 좋을수록 Perplexity는 낮겠죠. 다음에 오게될 단어가 비교적 확실하다는 것이니까.