[개념정리] 5. Off-Policy Control and Q-learning

temp·2021년 9월 5일

Off-policy control reinforcement learning

Reinforcement Learning

목록 보기

5/8

이전의 MC와 TD 방법은 모두 on-policy control였습니다. 즉, 현재 action의 기반이 되는 policy와 improve하는 policy가 같습니다.
하지만, 이 on-policy control의 경우 greedy improvement를 진행할 때 한계가 있고, 이를 $\epsilon$ -greedy improvement로 개선할 수 있었습니다.
이외에도 off-policy control(prediction + policy improvement)로 문제를 해결할 수도 있어, 본 글에서는 그에 대해서 다루겠습니다.

action의 기반이 되는 policy를 behavior policy라 하고, improve하는 policy를 target policy라 하자. 이 때, off-policy control는 behavior policy와 target policy를 다르게 취하게 된다.

off-policy control을 진행할 경우 장점은 아래와 같다.

인간이나 다른 agents로부터 학습 가능하다.
이전의 policy들인 $\pi_1, \pi_2, ..., \pi_{t-1}$ 로부터 나온 경험을 재사용할 수 있다.
exploratory(탐험적) policy를 따르는 동안에 Optimal Policy를 학습할 수 있다(Q-learing).
하나의 policy를 따르는 동안에 multiple policies를 학습할 수 있다.

Importance sampling

Importance sampling은 off-policy control이 어떻게 optimal policy를 학습할 수 있는 지를 보여준다.

In statistics, importance sampling is a general technique for estimating properties of a particular distribution, while only having samples generated from a different distribution than the distribution of interest

한 마디로, 알고자하는 모집단 분포의 parameter를 다른 분포의 샘플링을 통해서 추정하는 방법이다. 모집단의 분포를 모를 때에는 Monte-Carlo 방법처럼 random sampling을 통해서 값을 추정할 수 있는데(MC approximation), 이 경우 문제가 생길 수 있다.

보통 많은 응용 분야에서 $\mu =\mathbb{E}(f(X))$ 를 계산할 때가 많습니다. 이 때, 관심이 있는 확률변수 $X\in A$ 에 대해 영역 $A$ 를 제외한 영역에서 $f(x)$ , 즉 확률 값이 거의 0에 가깝다면 어떻게 될까요?
가령, $A$ 가 $X$ 분포의 끝에 위치한다든가, 그냥 $A$ 가 그 자체로 작은 부피를 차지하고 있다든가.
이 때, 일반적인 Monte-Carlo방법을 적용하게 되면 $X$ 에서 나온 몬테카를로 샘플들은 영역 $A$ 한 점도 가지기 힘들 것입니다.
이런 문제는 고에너지 물리, 베이지안 인퍼런스, 희귀 사건 시뮬레이션, CG 렌더링 등 다양한 분야에서 나타난다고 합니다.

또한, 여기서 말하는 $f(X)$ 는 강화학습의 목표가 되는 value function : expected future rewad로 생각하면 됩니다.

이러한 문제를 해결하기 위해, 관심이 있는 확률변수 $X$ 가 속하는 $A$ 의 크기가 너무 작아 $P(X)$ 가 0에 가까울 때, 이를 추정하기 위해 다른 분포를 통해 이를 추정하고, 다시 원래 분포에 맞게 조정해주는 방법이 Importance sampling이다.

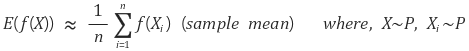
예를 들어, $\mu(\mathbb{E}(f(X)), X~P)$ 를 추정할 때, sampling된 값들을 이용해 sample mean을 이용할 수 있다. 하지만 앞과 같은 문제가 있어 sampling이 어려운 경우 trick으로 새로운, 다른 분포 $Q$ 에서 샘플링을 하고, 기존의 분포 $P$ 에 맞춰줄 수 있다.

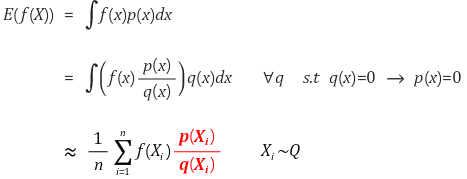
이처럼 $P$ 의 통계량을 구하기 위해 $Q$ 를 이용해 구할 수 있으며, 이 때 ${{p(X_i)}\over{q(X_i}}$ 를 importance weight이라 한다.

이처럼 통계량을 구하기 위해 적분 식을 변형하는 시도는 MC-method의 전형입니다.

수식

MC-method

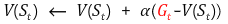
기존의 식에서 문제가 되는 부분인 Reward $G_t$ 인

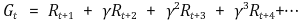
에 대해 아래와 같이 importance weight를 sequential하게 곱해주면 된다.

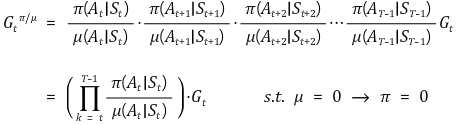
따라서 최종 update는 아래와 같다.

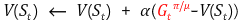
Off-policy TD prediction

TD에서는 target 값인 $R_{t+1}+\gamma V(S_t)$ 에 대해 한 스텝만 importance weight를 구해주면 된다.

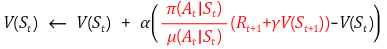
Q-Learning

Importance sampling의 경우 MC에서 q(x)만 잘 설정해준다면 on-policy MC보다 variance를 낮출 수 있다.

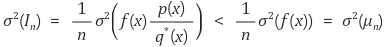
여기서 $p(x)$ 는 샘플링 될 확률이 낮기에, 보통 $q(x)$ 가 더 큽니다.

문제를 이렇게 설정하면, 결국 optimal $q(x)$ 인 $q^{*}(x)$ 를 찾는 문제로 회귀한다. 뿐만 아니라 TD에서도 기존의 on-policy 방법에 비해 off-policy 방법의 variance가 높다.

이를 해결하는 것이 Q-Learning

Q-Learning

1) 현재의 state $S$ 에서 behavior policy인 $\mu$ 에 따라 action $A$ 를 선택한다( $A_{t+1}=\mu(*|S_t)$ ).
2) q-func.을 이용하여 update하는데, 다음 state $S'$ 에서의 action $A$ 는 $\pi$ 에 따라 선택($A'=\pi(*|S_t).

Q-Learning은 Importance sampling을 필요로 하지 않는다.

다음 state $S'$ 에서의 action을 alternative policy에서 취하게 될 경우 Importance sampling이 필요하지 않습니다. 이전의 off-policy 방법에서는 value function을 사용했었지만, 여기서는 action-value function을 사용하기에 다음 action까지 선택하게 됩니다.

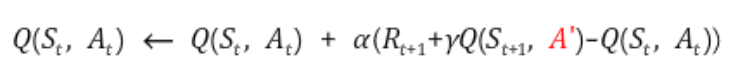
Off-policy Control with Q-Learning

Off-policy의 주된 장점은 explorator(탐험적) policy를 따르면서도 optimal policy를 학습할 수 있다는 것인데, 이를 해낸 것은 아래의 알고리즘이다.

Behavior policy : $\epsilon$ -greedy w.r.t $Q(s,a)$
Target policy(Alternative policy) : greedy w.r.t $Q(s,a)$

Greedy한 policy로 학습을 진행하면 당연하게도 수렴은 빨라지지만, 충분한 탐험을 거치지 않기 때문에 local optima에 빠질 위험이 큽니다.
그렇기 때문에 탐험을 위해 $\epsilon$ -greedy policy를 사용하게 되면 전역적으로 더 좋은 optimal policy를 찾을 수 있지만, 반대로 수렴 속도가 늦어져 학습이 지체됩니다.

위와 같은 Greedy, $\epsilon$ -greedy의 trade-off 관계를 약간이나마 보완하기 위해 $\epsilon$ 을 시간에 따라 decay 시키면서 Q-Learning을 함께 사용할 수 있다.

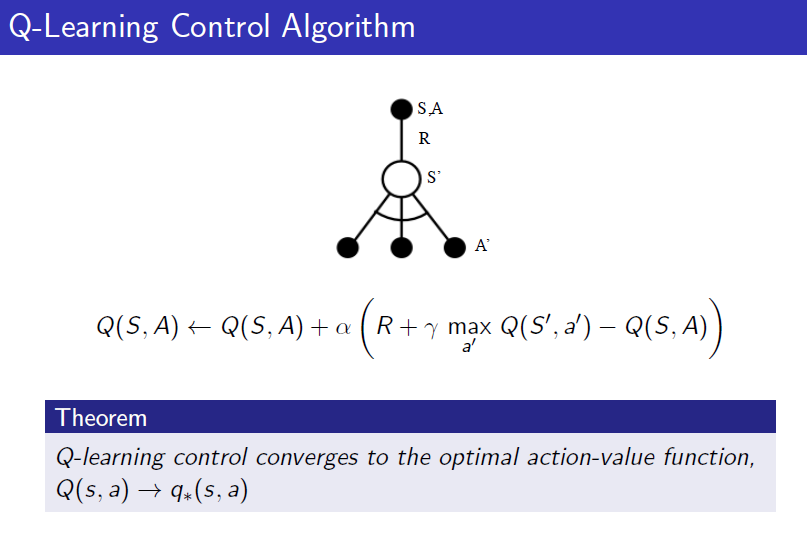
위의 알고리즘은 Bellman Optimality Equation을 사용한 value iteration을 이용한 것이다. optimal value function의 관계식을 이용하기 때문에 optimal action-value function에 수렴하게 되는 것.

SARSA vs Q-Learning

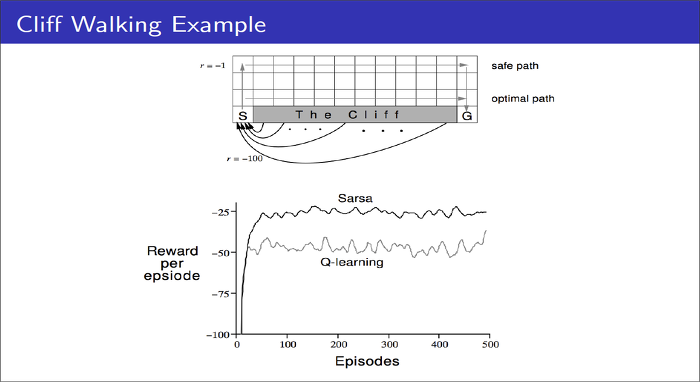
위의 예제인 Cliff Walking를 살펴보자.
목표는 당연히 최대의 Reward(즉, 최소 거리 + 절벽 회피)에 도달하는 것이다. 사람에게는 너무나도 쉬운 문제지만, 이를 강화학습으로 풀게될 경우 마냥 쉽지만은 않다.

SARSA 입장에서, $\epsilon$ -greedy policy를 취할 경우 이곳 저곳 Exploration을 하다가 cliff에 빠질 경우 cliff 주위의 state는 모두 낮은 value function을 갖게 된다.

반면, Q-Learning 입장에서, $\epsilon$ -greedy policy를 취하고, cliff에 빠질 지언정 action-value function만 낮아지기 때문에 cliff 근처의 state에는 도달할 수 있다. 단지, cliff 쪽으로 action만 하지 않으면 된다고 학습하는 것이다. 그렇기에 SARSA보다 효율적으로 optimal path를 찾을 수 있다.

이후 흐름

이전까지의 learning은 state와 action pair 경우의수가 적기 때문에 실측 값으로 계산이 가능했습니다. 하지만 조금 복잡한 게임만 하더라도 모든 경우의수를 고려할 수 없기 때문에 함수화 모델링을 통해 실측 값을 근사하여 사용하자는 아이디어가 자연스레 나왔습니다. 이를 통해 아무리 많은 경우의 수일지라도 모든 data를 저장하지 않고 학습이 가능하며, 이를 value function approximation이라 한다.