[개념정리] 4. Monte Carlo and Temporal-Difference Methods

이전 글에서는 DP의 연산량 문제, 모델 필요성 등의 단점을 해결하기 위해 Sample backup과 관련된 방법들이 쓰인다고 했습니다. 이 중 대표적인 Monte Carlo방법과 Temporal Difference 방법에 대해 간략하게 다루어봅시다.
특히, 위의 두 모델은

Monte Carlo의 경우 episode가 끝날 때 sampling 된 state들을 이용해 value function을 update하는 방법이다. 하지만 Temporal difference의 경우 time-step마다 한 단계씩 update를 진행한다.

아래에서는 terminal state까지 샘플링 된 state들과 reward들을 저장한 다음, 이를 바탕으로 state들의 true value function을 얻는 과정인 Monte-Carlo Prediction에 대해서 간략히 다루어보자.

Monte-Carlo

강화학습에서의 몬테카를로를 다루기 전에 기존의 통계 관련 분야에서 널리 쓰이는 몬테카를로 방법에 대해 간단히 살펴보자.
몬테카를로는 sampling 관련 optimization 기법 정도로 생각하면 된다.
즉, 위 그림과 같이 랜덤 샘플링을 통해 추정하고 싶은 값을 근사하는 것입니다.

실제로 고차원 함수의 최적화를 위해 MCMC를 굉장히 많이 사용하는 데, 이 때 MCMC의 풀네임이 Monte Carlo Markov Chain 입니다.

강화학습에서의 Monte-Carlo는 어떤 개념일까?

The term "Monte Carlo" is often used more broadly for any estimation method whose operation involves a significant random component. Here we use it specifically for methods based on averaging complete returns

Montero Carlo는 연산 과정에서 random한 구성 요소가 많을 경우에 사용할 수 있는 Estimation 방법이다. 강화학습에서는 완전한 return을 평균내는 방법을 기반으로 한다.

Monte-Carlo prediction

Monte-Carlo 방법에서는 episode를 샘플링(즉, terminal state까지 state 진행)을 한 다음, 이 때 받은 reward를 토대로 discount factor를 적용해 value function을 구하면 된다.

DP 문제에서는 이를 Bellman 방정식을 통해 구했지만, Monte-Carlo 방법에서는 이 reward들의 합의 평균을 통해 value function을 근사하게 된다.

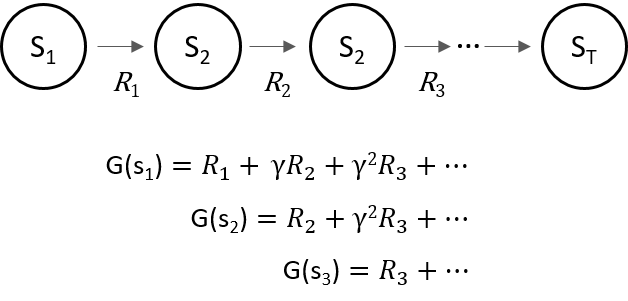
위처럼 임의의 policy에 대해 하나의 episode가 정해졌을 때, 각 state마다 구해진 Reward를 토대로 state별 return 값(여기서 $G(s)$) 를 구할 수 있다.
Monte-Carlo는 이러한 episode를 많이 반복해, 특정 state $s$를 지나는 모든 episode에서 해당 state $s$의 return 값 $G(s)$를 모두 구한 다음 평균을 내줌으로써, true value function으로 근사할 수 있다.

기존에서는 여러 번의 iteration을 통해 value function을 update한다.

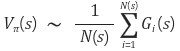
$N(s)$ : 총 episode 동안 state $s$를 방문한 횟수
$G_i(s)$ : episode $i$에서 state $s$의 return 값

실제로, 위의 식에서 $n$개의 return 값을 받은 뒤 추정하게 될 $value function$을 $V_{n+1}$으로, $N(s)$를 편의상 $n$으로, 그리고 state는 $s$ 하나로 고정한다면 아래와 같이 식을 전개할 수 있다.

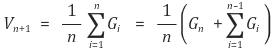
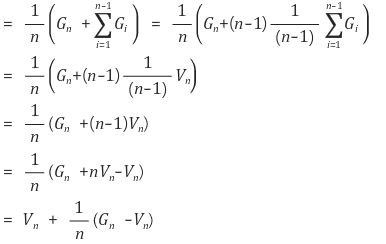
즉, 가장 최근의 value function $V_n$에서, 가장 최근의 Return 값 $G_n$의 차이를 줄이는 방향으로 $n$개의 Return값을 받은 이후의 value function 값인 $V_{n+1}$가 정해진다(즉, update) 할 수 있다.

이처럼 Return 값을 모두 모아 한 번에 평균을 내는 것이 아닌, 새로운 return 값을 얻을 때마다 update하기 때문에 아래처럼 incremental mean의 형태로 나타낼 수 있는 것이다.

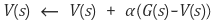
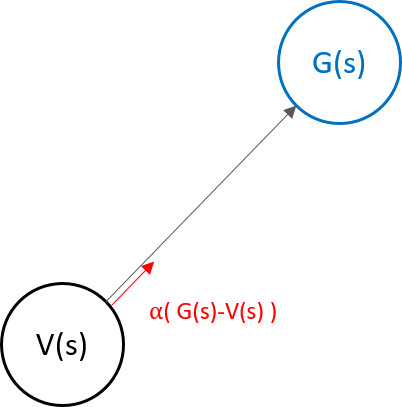
위의 그림에서 Return G의 방향으로 value function V가 업데이트 되는 모양임을 알 수 있다.

위의 업데이트 과정에서, 한 episode 내에서 같은 state를 두 번 이상 방문할 경우, 첫 방문 시의 return 값을 고려할 것인지 방문할 때마다 생긴 모든 return 값을 고려할 것인지에 따라 first-vist MC와 Every visit MC로 나뉩니다.

Monte-Carlo Control

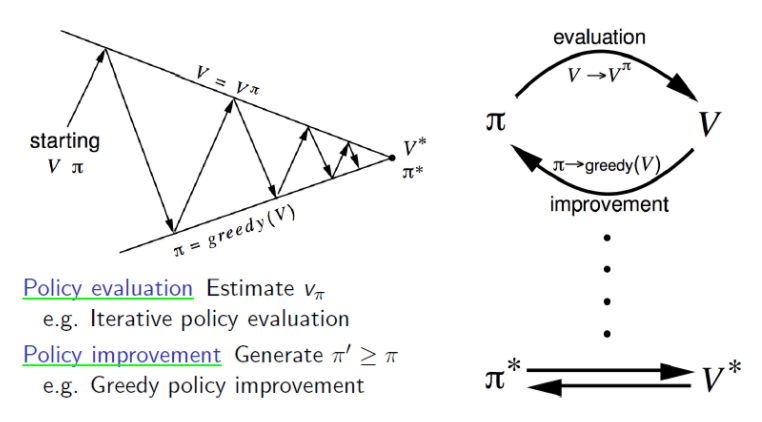
DP에서 Policy iteration은 evaluation과 improvement로 나뉘었었다. 여기서 evaluation 단계에 MC를 이용한다면 Monte-Carlo policy Iteration이라 할 수 있다.

• Policy Iteration = ( policy evaluation + policy improvement )

• Monte-Carlo policy Iteration = ( MC policy evaluation + policy improvement )

하지만, MC policy Iteration에는 아래와 같은 단점이 존재한다.

1. Value func.의 model-based
2. Local optimum
3. Inefficiency of policy evaluation

이를 해결하기 위해 Monte-Carlo Control을 도입한다.

1. value function의 특징, Model-based

MC를 이용해 improvement를 진행하더라도 value function이 필요한데, 이 말은 model을 알아야 한다는 말과 동일하다.

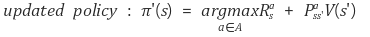
이를 해결하기 위해 value function 대신 action-value function(q-function)을 사용합니다.

자세히 다루어보자.

value-function을 이용할 경우에는, agent가 episode마다 얻은 reward들로 state의 return 값을 게산하고, 이를 평균 내 state마다 value function을 구해놓는다. 하지만 improvement 단계에서 policy를 업데이트 하기 위해 reward와 state transition prob을 알아야 한다. 즉, q-function을 이용해서 policy를 업데이트 하기 위해서,

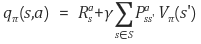
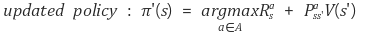
위의 식들처럼 model이 필요하다.

action-value function을 이용할 경우에는, episode마다 random하게 움직이며 얻은 reward들, 그리고 state transition prob을 통해 action-value function을 계산할 수 있다. 이 경우 policy를 improve할 때 model을 모르더라도 이미 전 과정에서 action-value function(q-function)을 계산했기에 모델의 정보가 다 담겨 있다고 할 수 있다.

즉, model-free 하다는 것은 policy를 improvement할 때의 얘기이고, episode를 샘플링하는 과정에서(즉, trail and error의 과정에서) 모든 정보가 q-function에 담겨 있기 때문에 이를 그냥 선택해서 사용하면 된다는 이야기입니다.

Local optimum

이는 웬만한 Optimization(Estimation)하는 과정에서 발생할 수 있는 문제이다. 이전의 글에선 주로 greedy policy improvement를 사용했기에 이 과정을 통해 얻어진 해가 global하게 좋은 해인지는 장담하지 못한다. 이를 해결한 것이 $\epsilon$-greedy policy improvement이다.

요약하면, $\epsilon$의 확률로 exploration(random action)을 하고, $1-\epsilon$의 확률로 최적의 해(optimal policy)를 택하는 방법이다.

이렇게 특정한 확률에 따라 더욱 많은 가능성을 가진 영역을 탐색하는 방법론은 굉장히 다양한 Optimization 기법들에 쓰입니다.(ex, Simulated Annealing).

Inefficiency of policy evaluation

DP에서는 Policy iteration 과정에서 optimal policy라는 전제와 함께 q0function을 이용하여 한 번만 evaluation하는 value iteration이 있었다. 마찬가지로 MC control에서도 Evaluation을 단 한번만 진행하게 된다.

Temporal Difference Method

Temporal Difference Method의 모티베이션 정도만 다루고 넘어가겠습니다.

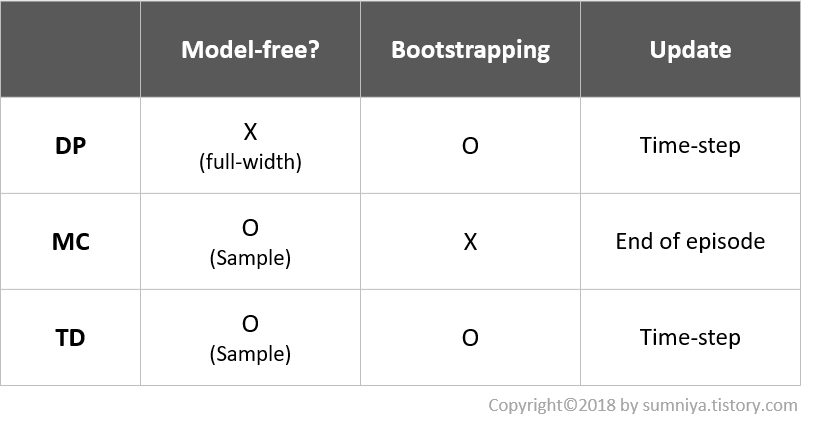
Temporal Difference Methods는 Monte-Carlo와 마찬가지로 model-free한 방법이다. MC는 한 episode가 끝난 후 얻은 return 값을 이용해 각 state의 value function을 업데이트 한다. 반면, atari 게임이나 real-world problem 같은 경우 episode의 끝이 무한대에 가깝도록 길다. 그렇기 때문에 episode가 반드시 끝나야 학습을 하는 MC의 방법으로는 한계가 존재하는 것.

이를 보완하기 위해 DP처럼 time-step마다 학습하는 방법이 TD(Temporal Difference) 방법이다.

TD는 MC와 DP의 아이디어를 조합한 방법으로, MC처럼 model-free하게 순수한 경험만으로 Learning을 할 수 있으며, DP처럼 episode의 끝을 기다리지 않고 update한다. 이 때, Bootstrap이란 단어가 중요하다.

Bootstrap

In statistics, bootstrapping is any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy (defined in terms of bias, variance, confidence intervals, prediction error or some other such measure) to sample estimates. (wikipedia)

Bootstrap은 랜덤 샘플링을 복원추출의 방법으로 진행해 가설 검정을 하거나 metric을 구하는 방법이다. 이 때, 모집단의 분포에 대해 어떠한 가정도 없이 랜덤 샘플링을 진행해 모집단의 metric을 추정할 수 있다. 즉, 사실상 분포를 구하는 게 거의 불가능한 현실 문제들에 대해서도 그 분포의 metric에 대해서 알 수 있는 것이다.

RL 관점에서 볼 때, Bootstrap은 추정에 근거한 update라 할 수 있다. DP나 TD는 time-step 별로 이전의 value function을 통해 현재의 value function을 추정할 수 있다.

sampling은 말 자체가 model-free한 속성과 관련되어 있어 sample backup과도 연관된 개념입니다. 하지만 DP는 full-width backup이였기에 model-free하다고 보기는 어렵습니다.

TD Prediction

가장 기본적인 TD에 대해서만 다루고 넘어갑시다.

아래 식은 우선 MC에서 value function을 update하는 식이다.

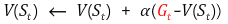
이 때, return $G_t$는 해당 state $S_t$에서 episode의 끝까지 얻은 reward를 시간에따라 discount한 값이다. 이를 1 step에 대한 것으로 바꾸면 TD(0)이 되며, 식은 아래와 같다.

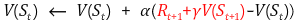
위에서 빨간 색으로 나타난 $R_{t+1}+\gamma V(S_{t+1})$를 TD target이라 하고, $R_{t+1}+\gamma V(S_{t+1})-V(S_t)$를 TD error라 한다. 아래의 알고리즘을 보면 더욱 이해하기 좋다.

MC vs TD

직장에서부터 집까지 운전을 해서 가는 episode에 대한 예측 문제입니다.

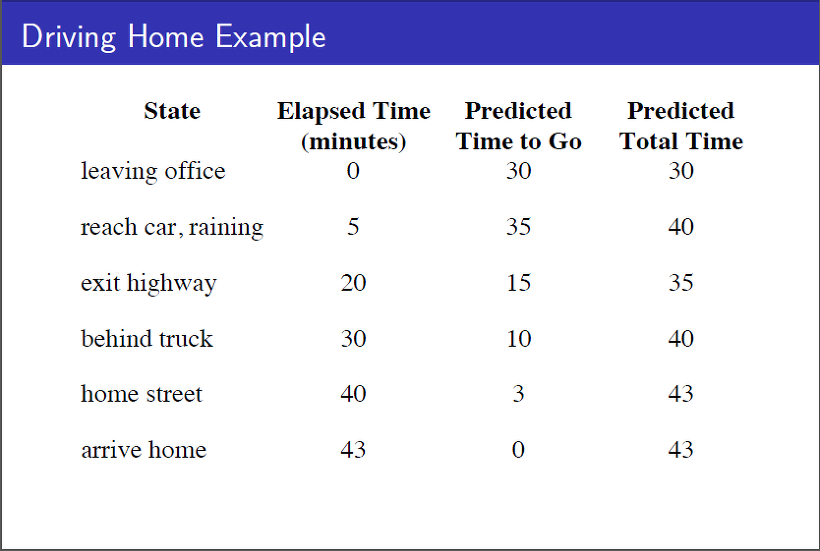
이 때, 각 state에서 집까지 걸릴 시간이 value function이다(value function의 정의). agent는 각 sate에서 다음 state로 이동할 때 실제 걸린 시간을 reward라 가정하고, 이를 바탕으로 value function을 update하는 것이다. 업데이트가 충분히 되고 나면, agent가 total time을 predict하고, 이를 바탕으로 state의 value function을 predict할 것이다.
아래 그림은 agent가 예측한 total time을 state에 따라 plotting한 것이다.

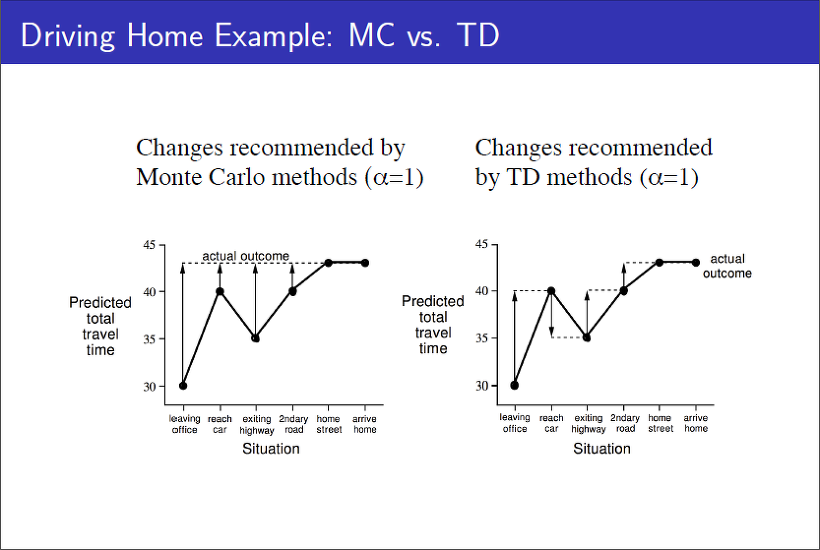
보다시피, MC 방법은 실질적으로 episode가 끝나고 얻은 값인 "actual outcome"을 이용해 각 state별 value function의 update가 일어나는 반면, TD 방법은 바로 이후 state의 value function과 Reward를 이용해 state의 value function을 update하는 것을 알 수 있습니다.

다만, TD는 바로 다음 step의 error만을 고려하기 때문에 학습도 오래 걸리고, 한 쪽으로 치우칠 수 있다.

다음 step의 value function이기에 정의 상 그 뒤의 reward까지 포함하고 있지 않냐? 라고 생각할 수 있지만, 이는 실제로 얻은 reward를 바탕으로 계산한 값이 아닌 "추정"이기 때문에 true value로 update할 "여지"정도로만 보는 것이 좋습니다.

그렇기에, TD는 어느 정도 bias가 높다 할 수 있다.

반면, MC는 episode가 끝나면 update하기 때문에 실제 얻은 reward의 정보를 반영할 수 있습니다. 하지만 episode가 어떤 state sequence로 이루어져 있느냐에 따라서 동일한 state도 각기 다른 value function으로 update될 수 있다.

그러니, MC는 variance가 높다할 수 있다.

위의 bias와 variance는 trade-off 관계이다. 학습에 어느 정도 방해가 되는 요소이기 때문에 이를 줄이기 위해 다양한 방법들이 존재한다.

variance는 학습(특히 Exploration)에 도움이 된다고 할 수 있지 않나?

n-step TD

n-step TD는 update할 때 하나의 step가 아닌, n개의 step을 보고 update하는 것이다.

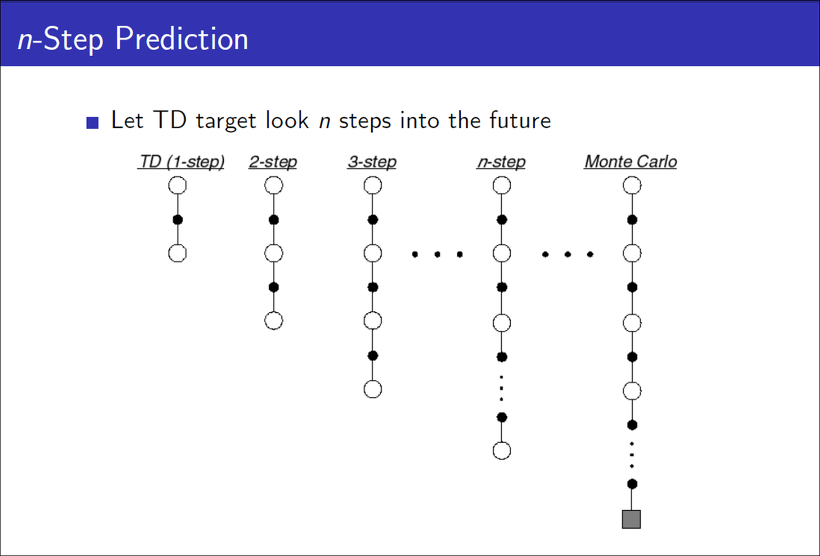
위와 같은 방법으로 MC와 TD의 장점을 부분적으로 취할 수 있습니다.

만약 n이 Terminal state까지 도달할 수 있다면 그건 MC라 할 수 있겠죠.

위와 같은 방법 외에도 TD($\lambda$), forward-view TD($\lambda$), Backward-view TD($\lambda$) 등 방법이 존재한다.

또한, MC Control처럼 TD Control이 존재해 SARSA, n-step SARSA, SARSA($\lambda$) 등이 존재한다.

본 글에서 다룬 방법인 MC와 TD는 강화학습의 대표적인 방법입니다. 이는 모두 on-policy RL인데, 이 모델들의 단점을 해결하기 위해 off-policy 방법인 Q-learning을 다룰 것입니다.
위에서 말하는 단점은 greedy하게 움직일 경우 optimal에 다다르지 못할 확률이 커지는 문제입니다.