Some Note on VAE

용어 정리

• latent(vector): 잠재 벡터. 즉, 데이터를 생성하는 데 관여하는 분포로, feature를 가지는 vector이다. 보통 우리의 목표이다.
• intractable : 문제를 해결하기 위해 필요한 시간이 문제의 크기에 따라 지수적으로(exponential) 증가한다면 그 문제는 난해(intractable) 하다고 한다.
• explicit density model : 샘플링 모델의 구조(분포)를 명확히 정의
• implicit density model : 샘플링 모델의 구조(분포)를 explicit하게 정의하지 않음
• density estimation : $x$라는 데이터만 관찰할 수 있을 때, $x$가 샘플링된 (관찰할 수 없는) 샘플링된 확률밀도함수를 추정하는 것.
• Gaussian distribution : 정규분포
• Bernoulli distribution : 베르누이 분포
• Marginal Probability : 주변 확률 분포
• $KL_D$ : 쿨백-라이블러 발산(Kullback-Leibler Divergence, KLD). 보통 두 확률분포의 차이를 정의하기 위해 사용

용어정리 출처 : https://taeu.github.io/paper/deeplearning-paper-vae/

Idea

• 확률 분포에 대한 parameter를 학습이 제대로 완료되면, 이를 통해 샘플링을 할 수 있기 때문에, 무궁무진한 활용이 가능하다.

  가령, n개의 데이터를 샘플링해서 평균을 낸다든지, 이론적인 Expectation 대신 Sample mean을 사용한다든지..

• original 고차원의 공간을 저차원의 매니폴더를 축소했을 경우, 매니폴드에서의 데이터 좌표가 변함에 따라 original 고차원 데이터 또한 (유의미하게)변화한다(물론, 고차원 데이터의 특징을 잘 모사하는 좋은 매니폴드를 찾았을 경우겠죠?).
  

출처 : https://deepinsight.tistory.com/123

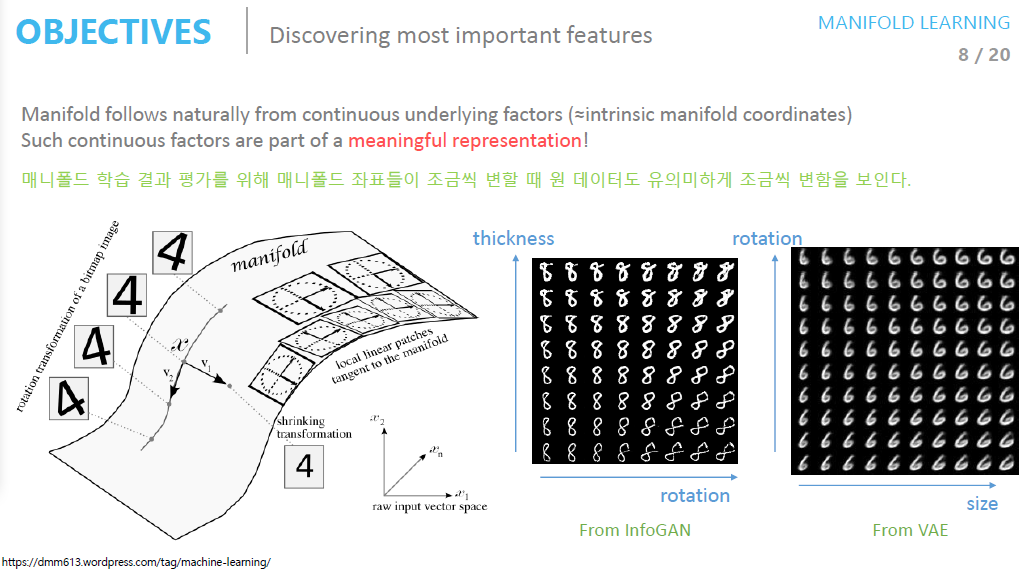
Distribution

• 크로스 엔트로피를 최소화 한다는 것은, 마치 이항분포(혹은 다항분포)를 최대화하는 것과 유사하게 바라볼 수 있다.
  

• 또한, MSE를 최소화 한다는 것은, 가우시안 분포를 최소화 하는 것과 같이 바라볼 수 있다.
  

즉, 정답 값과 예측 값의 차이를 단순히 거리 & 엔트로피 개념(loss)으로 바라볼 것인지, 확률 & 분포의 개념(MLE)으로 바라보는 것은 근본적으로 큰 차이가 없다는 것.

출처 : https://deepinsight.tistory.com/123

Autoencoder

• VAE와 오토인코더(AE)는 목적이 다르다.
• 오토인코더의 목적은 어떤 데이터를 잘 압축하는 것, 데이터의 특징을 잘 뽑아내는 것, 데이터의 차원을 잘 줄이는 것이다.

Encoder

• Input data를 잘 복원할 수 있다.
• 최소한의 성능은 보장한다(GAN은?)
• Input data의 Feature를 추출할 때 많이 사용한다.
• 차원 축소에 자주 사용한다.

Decoder

• Training data를 만들어줄 수 있다.

• 반면, VAE는 생성모델로, 어떤 새로운 $X$를 잘 만드는 것을 목표로 한다.

VAE

• VAE는 Generative Model이다.
• 학습이 잘 됐다는 가정하에, latent vector인 $z$는 original image를 control할 수 있다(특징을 조절할 수 있다).
• 기존의 Train dataset과 유사한 샘플을 생성하기 위해 사전분포로 가우시안분포(정규분포)를 가정하는데, Deep Neural Network의 특성때문에 정규분포로도 저차원의 manifold를 잘 표현할 수 있다고 한다.
• 샘플링 함수를 통해 샘플링을 한 뒤 나온 생성 데이터를 실제 데이터 $x$에 가깝게 하는 것이 VAE의 목표.

1. 의미론 적으로 가까운 sample들을 생성해내는 $z$ 정의
2. $z$를 생성할 수 있는 이상적인 sampling 함수 정의
3. $x$를 given으로 주어 학습 진행.

Vanilla VAE

• $p(z), q(z|x)$를 가우시안으로 하는 이유는 KL 발산이 closed form으로 계산이 되고, 가우시안 분포가 샘플링하기 쉽기 때문에 generate측면에서 좋기 때문이다. 만약 vae with vamp-prior 등 다른 방식의 prior를 사용하는 경우도 있긴 하지만, 이 경우 KL 발산의 term을 근사적으로 계산하게 될 것이다.

• blur문제는 가우시안에 의한 영향이 분명히 있다.
• KL 발산 과정에서 MSE형태로 변하기 때문에, Latent dim이 너무 작으면 복원하는 과정에서 차원의 한계로 blur한 형태로 복원될 수 밖에 없는 것.
  -이 한계를 해결하기 위해 층을 여러 개 쌓아서 활성화함수로 차원을 꺾어줌으로써 더 sharp한 표현을 하고자 구현할 수도 있다.
• 즉, latent vector $z$에 조금 더 계층(hierarchy)이 있는 구조를 부여함으로써 나이브한 가우시안보다 조금 더 유연한 $q(z|x)$를 도출할 수 있는 것?

• Latent sapce의 디멘션과 이미지의 디멘션을 동일하게 설정하는 경우가 있다. augmented normalizing flow는 latent space를 조절하고, 부족한 dimension에 대해 ELBO를 취하는 메소드가 있다. 이는 latent space가 이미지 크기보다 작은 VAE의 일반화 버전으로 여길 수도 있을 것.

VAE loss

• Loss = reconstruction error($||x-\hat{x}||$)+ KLD (latent error)로 구성.

• -ELBO = BCE + KLD로 표현 가능.

• 이미지는 보통 베르누이를 따른다는 가정이 있어 bce loss를 사용한다.

• loss가 mse냐 bce냐 결정하는 것은 $p_\theta (x|z)$가 어떤 분포를 따를 것이냐는 '가정'에 의존한다.
  - 정규분포를 가정하면 mse, 베르누이를 가정하면 bce.

• KL divergence term은 $p(z)$와 $q_\phi (z|x)$ 사이의 거리를 줄이는 것.

• maximize $logp(x|z)$를 하는 것이 reconstruction loss term**이라 할 수 있다.

KL divergence

• KL Divergence에서 $log(p(x|z))$대신 variation과 mean으로 된 수식을 사용할 수 있다(당연히 가우시안 분포를 가정).

  https://leenashekhar.github.io/2019-01-30-KL-Divergence/

• KL 발산의 식은 아래와 같다.
  
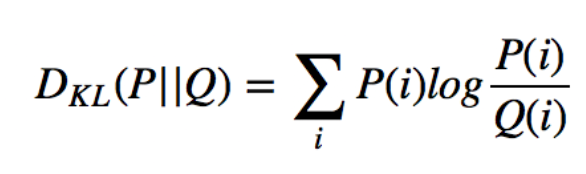
• 이는, 사전확률 $Q$에서 사후확률 $P$로 갈 때 얻는 정보의 양 정도로 해석할 수 있다. 즉, 근사모델 $Q$를 실제 모델 $P$와 가깝게 만들기 위해, KL 발산을 최소화하는 방향으로 학습을 진행하는 것.