참고 논문 : A Modified SIR Model for the COVID-19 Contagion in Italy

본 글은 메모용으로 작성하였기에 참고하기에 적절하지 않을 수 있습니다.

원 글 작성일 : 2020-08-23

SIR 모델에 관한 고찰과, 수학적 이론

A Modified SIR Model for the COVID-19 Contagion in Italy.

• 장,단기 예측을 할 수 있는 Modified SIR 모델은 정책 책임자들이 containment measure, lockdowns, and vaccination compaings(예방접종) 같은 정책을 결정하는데 판단 근거를 준다.
• 전염병의 time evolution을 예측하는 데에는 collective model과 networked model이 존재한다.
• Collective model은 적은 수의 parameter와 적은 수의 collective variables로 전염병 확산을 묘사한다.(ex, growth model, logistic model, Richards model, Generalized Richards model, sub-epidemics wave models 등)
• 거기에 추가로, SIR, SEIR모델까지 포함해서 소위 compartmental(구획,칸막이) models 로 불린다.
• Networked model은 굉장히 많은 수의 parameter와 variables을 사용해야하고,
  network topology는 실 세계의 상황에 있어서 잘 안 알려져있으며 증명 자체가 너무나 어려운 일이다.(전문가를 위한 이론)

고로, 일반적인 사용자에게는 Collective model이 다루기 쉬우며, 이는 비교적 작은 데이터로도 어느정도 믿을 만한 결과를 도출한다.

• Collective model은 보통 Differential equations 또는 discrete-time difference equations으로 나타나며 선험적으로 알려지지 않은(경험하기 이전엔 참,거짓을 판단할 수 없는), 그렇기 때문에 data로부터 식별되어야 할(have to identified) 여러 parameter들로 구성이 된다. 다만 이러한 parameter의 identification은 여러 실전적인 issue를 불러 일으킨다.

identifications of system ?

White-box identifications

• 모델의 parameters를 data로부터 추측한다.

Gray-box identification

• 일반적인 모델 구조가 주어진 상태에서 parameters를 data로부터 추측

Black-box identification

• data로부터 모델 구조를 결정하고, parameters또한 추측한다.

전염병 모델에서 가장 중요한 variable은 감염자인데, 사용 가능한 정보는 오직 “positive”한 cases이고, “실질적인 확진자”는 알 수가 없다(issue 1).

• 이 모델에서는, 우선 Observed cases(어떤 경우를 말 하는건지)도 확진자로 가정한다(잘못 된 결과 도출 될 가능성 있음에도 불구하고).
• 즉, 어느정도 완벽하지 않아도 된다(그리고 그건 불가능하다).

identification of epidemic models은 많은 경우에 non-convex optimization problems을 다루어야 한다(issue 2).

convex optimization problems

• 우선, linear functions이 convex functions이다. (진짜 현실 세계의 문제를 non-linear 방식으로 해결해야 할까?)

• identification은 model의 multi-step prediction error를 최소화 하는 방향으로 수행되어야 한다 (각기 다른 통제 전략의 올바른 비교를 위하여)

  • 그를 위해선 non-convex optimizations problem을 풀어야함.

• SIR모델의 첫번째 장점은 실제 감염자의 수를 묘사하며, 이 수는 epidemiological standpoint(역학적 관점) 에서 굉장히 중요하다(위에서 말했다시피)
• SIR모델의 두번째 장점은, consists in(다음과 같이 구성된다) model identification and predictions frames-work(이는 위에 열거된 issue들을 극복하는데 도움이 된다 (infection evolution of covid-19에 있어서)

SIR모델이 어떻게, 위와 같은 non-convex optimizations과 multi-step predictions error를 해결할 수 있다는 걸까?

• SIR 모델의 Identifications approach는 단순하지만 실전적인 scheme(계획)을 기반으로 두는데, 이는 identified된 일련의 parameters를 가정한다?(해석X)
• nonlinear dependence(전문적 용어(terminology)로는, nonlinear parameters로 불리는) 적은 parameters(여기선 2개)를 다루기 위해서 grid is defined. (grid란 ?)
• grid의 각 지점에서 다른 parameter들은 convex optimizations을 통해서 identified된다.
• 결국, 이러한 접근(convex optimization)은 over the grid, 적절한 목적 함수(objective function)을 최소화하는 optimal한 parameter estimate가 선택된다.
  이는 특히 epidemic collective models에 도움되는데 이는 몇 안되는 개수의 nonlinear parameters로 구성되기 때문이다.
• 물론 변수의 양이 많아지면, 접근법은 컴퓨터적으로 실현할 수 없게 된다.
• 이러한 convex optimization으로 행해진 parameter estimate는 분명히 믿을 만하나, 장기적인 관점에서 예측은 극도로 정확하진 않을 것이다.
  (이는, convex optimization는 one-step prediction error는 최소화하지만 multi-step predction error는 최소화 할 수 없기 때문이다.

어쨌든 , multi-step prediction error를 극복하기 위해서 a novel long-term prediction algorithm을 채택했으며, 이 알고리즘은 가능한 모든 initial conditions에 대하여 simulations을 시작함으로써 수행되는 weighted average of the multi-step predictions을 기반으로 한다.

여러 conditions (parameter, initial conditions)등에 대해 컴퓨터 시뮬레이션을 돌려보고, 현실 세계와 가장 부합한 conditions을 채택하는 접근법과 비슷해보인다.

가중평균 (Weighted average)

• Weighted average is a calculation that takes into account the varying degrees of importance of the numbers in a data set.
• 이 접근법은, noise와 error effects를 감소시키는 쪽으로 작용하고, 이는 장기적인(long-term) 예측 정확성에 도움이 된다.

real-data에 관한 연구가 제시된다.

SIRD MODEL FOR COVID-19 CONTAGION

다른 지역으로부터 지리적으로 고립된 지역이라 가정하자.
S,I,R,D
S : 감염에 허용되어있는 집단.
I : 감염되어있는 집단(바이러스 활성화)
R : 누적 치료자
D : Deceased : 고인(누적)

이에 관한, discrete-time version of the Kermack-McKendrick equations는 다음과 같다.

모델에, 어떻게 parameter가 결정되는 지에 대한 증명.
https://www.cabdirect.org/cabdirect/abstract/19762902036

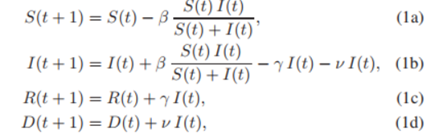
이 모델에 대한 의의는 알겠으나, parameter의 estimate와, 식 자체의 의도가 궁금하긴 하다. (논문에 접근 자체가 안 돼서 아직 확인하지 못함.

β : 감염률
γ : 회복률
ν : 사망률
여기서 t=0,1,2,… 는 days.

-이는 SIR 모델의 discrete-time 버전이다(어떻게 미분방정식에서, discrete-time으로 바꿀 수 있는건지.

모델에 대한 가정

1. 다른 지역으로부터 출,입은 없다고 가정(발전시킨게 중국의 논문)

• containment measure가 실행 된 경우는 고립이 타당하므로

2. 확진자가 다른 지병으로 사망한 경우는 무시한다 (판단 하기 복잡해서)

우선, 이 모델은 I(t)가 실제 확진자 수라고 가정하지만, 실제로는 observations 과정은 오직 일부분인 I ̃(t)만 탐지할 수 있다(무증상감염도 존재하므로 즉

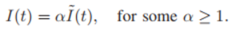
기 때문이다. 이를 모델에 대입하면,

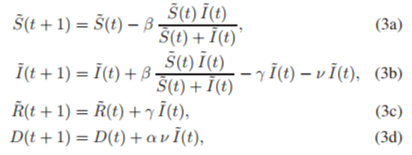
위 식은Weighted된 susceptible라고 보면 되고,
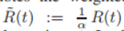는 deteced된 회복자로 보면 된다. 앞으론 이 Equations(3)이 SIRD모델로 불릴 것이다.
(가중치를 줌으로써, observable한 data를 가지고 비교할 수 있다.)
즉, 기초 논문은 “actual number”에 관한 부분이지만, 실제 covid-19 연구에서는 관측되지 않은 cases의 연구는 어렵기 때문에 보정해주는 거라고 볼 수 있다.

또한, 이 모델의 continuous-time 버전의 식을 보려고 했으나 역시 논문에 접근이 안 된다.

아무튼, 이러한 모델들은 initial conditions에 크게 의존한다.
이 두가지는, epidemic peak의 진폭(amplitude)와 위치(location)를 결정한다.
불행하게도, 기본적으로 인구의 일부는 감염에 선천적으로 내성이 있거나, 영향을 받지 않을 수 있기 때문에 그 지역의 총 인구를 S(t0)으로 잡는 것은 실제보다 over-estimation일 수도 있다는 점을 따져보면 , 모델을 설계하는 사람에게 S(t0)에 대한 자료(datum)은 이용 불가능 하다고 볼 수 있다.

이는 따져야 할 추가 변수.

아무튼, 이런 문제들 때문에 모델을 rendering하는건 굉장히 어려운 역할이다.
이 논문의 주 목적은, 대신 S(t0),𝛂,𝛃,𝛄, ν와 같은 parameter를 사용 가능한 data로부터 estimating하는 것이며, 이로 인해 COVID-19의 behavior를 더 정확히 예측할 수 있을 것이다.

MODEL IDENTIFICATION

이 섹션에서는, parameter들을 identifying하는데 쓰이는 과정을 자세하게 설명하겠다.
여기에 쓰인 data는 https://github.com/pcm-dpc/COVID-19 에 서술된 official data를 이용하도록 하겠고, 여기 나온 data는 를 나타내며 discrete time은 전염병의 발병일로 부터의 날짜 수이다. (2월 24일~ 3월30일-이탈리아)

• S집단의 수를 정확하게 나타내기 위하여 새로운 parameter를 도입하였다.
  
  

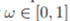
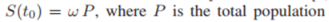
• 추가적인 variable들의 정의
  

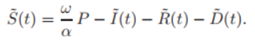
그러므로 , 고정된 값인 ω and α을 고려하면 Model(3)은 다음과 같이 regression(회귀) 형식으로 표현 가능하다.

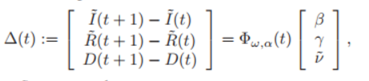
이때, υ ̃=αν이며,

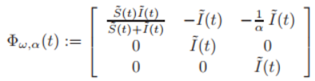
이다.

아래는, 참고하기 쉽게끔 Model(3)을 그대로 가져온 것.

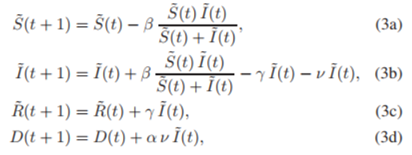
역시, 그저 간단히 나타낸 것 뿐이다.
가능한 Time window 안에서 weighted vectors인
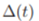와

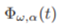
를 쌓음으로써 다음과 같은 행렬을 얻을 수 있다.

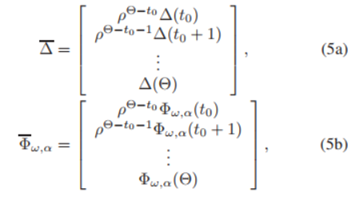
※ Time window : fixed interval of time when the data stream is processed for query and mining purpose
※ Weighting : 가중화 과정

역시, 이 식에서 ρ ∈(0, 1)은 parameter를 가중화하는 exponential decay(지수적 감쇠)라고 볼 수 있는데, 이는 최근 데이터에 더욱 관련성을 주기 위해서 정의 됐으며 θ는 time window의 길이이다(주어진 날짜길이)

그러면, parameter 𝛃,𝛄,ν ̃는 평균제곱최적화(mean square optimaztion)
문제를 품으로써 추정될 수 있다.


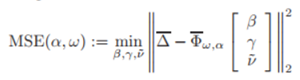
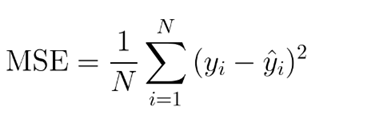
아마, 이는 실제 관측값과 예측값의 차이일 것.
또한 , 고정된 상수인 α,ω가 주어진다면, 이 최적화 문제의 해(parameter)는

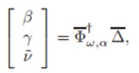
이고

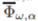
는 Moore-Penrose pseudo-inverse of matrix이다.(유사역행렬)

위의 최적화 문제는 convex하기 때문에 convex optimization method로 해결 가능함과 동시에, 문제

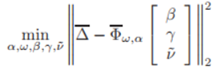
는 convex하지 않아도 된다는 점을 주목해보자.
예를 들면,
(not convex)
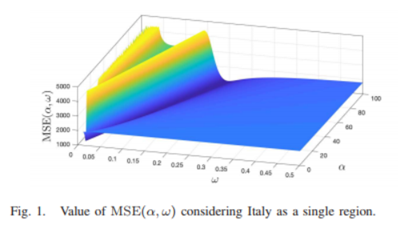
를 보면, ρ 값을 고정했을 때, MSE(α,ω)값이다. (α∈[1,100], ω∈[0,1])
즉, 만약 α,ω가 상수로 고정 됐다면 convex인데, 고정이 안 되어있다면 not convex라는 점이다.
그렇기에 바로 위에 정해진 parameter 5개에 대한 MSE모델은 컴퓨터적 해결이 다소 어려워 진다.(NOT-CONVEX하므로)

그럼에도 불구하고, α, β, γ, υ ̃and ω는 Algorithm 1을 사용함으로써 결정할 수 있고, 이는 model의 parameter를 computes한다(gridding함으로써, 데이터에 더 잘 맞게, 또한 (7)을 사용해서 MSE(α, ω)를 결정하고, 이에 대한 최소화 문제를 품으로써.)

α : 실제 감염자수(관측 불가능)와 관측 된 감염자수(관측 가능)의 차이변수
ω : 실제 지역의 총 인구(P)와 감염 가능한(S)의 차이변수

아래 나와있는 테이블은, 알고리즘1을 이용해 얻은 parameter이며, 단절되어있는 각 지역(region)또는 모든 이탈리아의 cases를 나타냈고, α ̅=100 – α의 최댓값(최대 범위), ρ=0.9로 가정하였다.
ρ=0.9로 가정 : 이는 맨 위의 식(5)와 (6)을 이해해보자.
그렇게 어렵지는 않다.

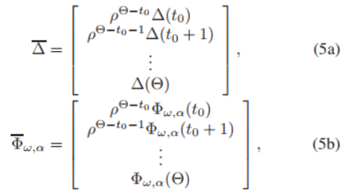
• 1일차는 가중치 ρ(미리 임의로 정해넣음, 여기서는 0.9 등)가 50번 곱해져있고, 2일차는 49번 곱해져있고….
  변수 위의 강조점은, 아마 쌓았다는 의미 인 것 같다(가중치를 주면서 0일부터 50일까지 나열)
• 또한, 아래 MSE 문제의 식도 가만 보면 그저 각 날짜마다 가중치를 주어서
  최소 제곱법을 풀었을 뿐이다.

parameter를 tuning하는 알고리즘을 통해 α,ω을 gridding(너가 아는그 의미)함으로써, MSE(α,ω)문제를 풀어, 나머지 매개변수를 결정할 수 있다.