로지스틱 회귀(Logistic Regression)

로지스틱 회귀란?

로지스틱 회귀 모델은 일종의 확률 모델로서 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계기법이며 종속 변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류(classification) 기법이기도 하다.

다음은 로지스틱 회귀 모델을 사용하는 예시이다.

• 제품이 불량인지 양품인지 분류
• 이메일이 스펨인지 정상메일인지

로지스틱 회귀모델의 이론

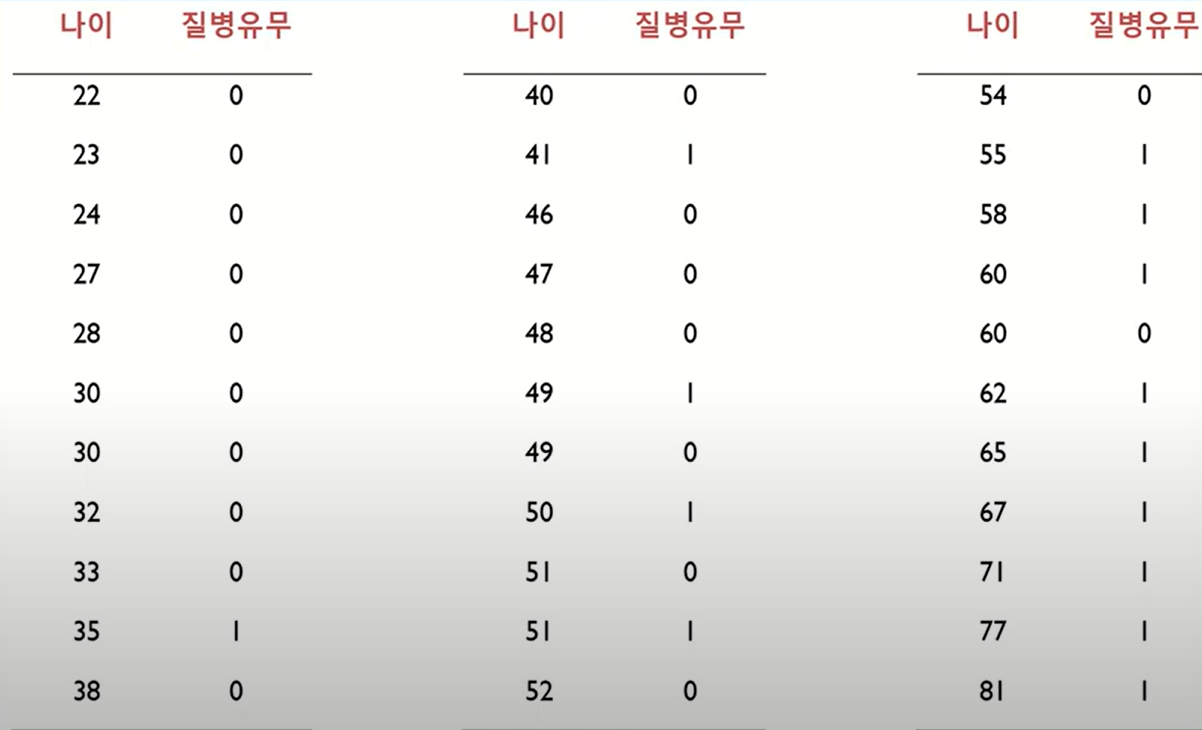
위의 독립변수(나이)에 따른 종속변수(질병유무)에 대한 데이터를 2차원 에 plot하면 다음과 같다.

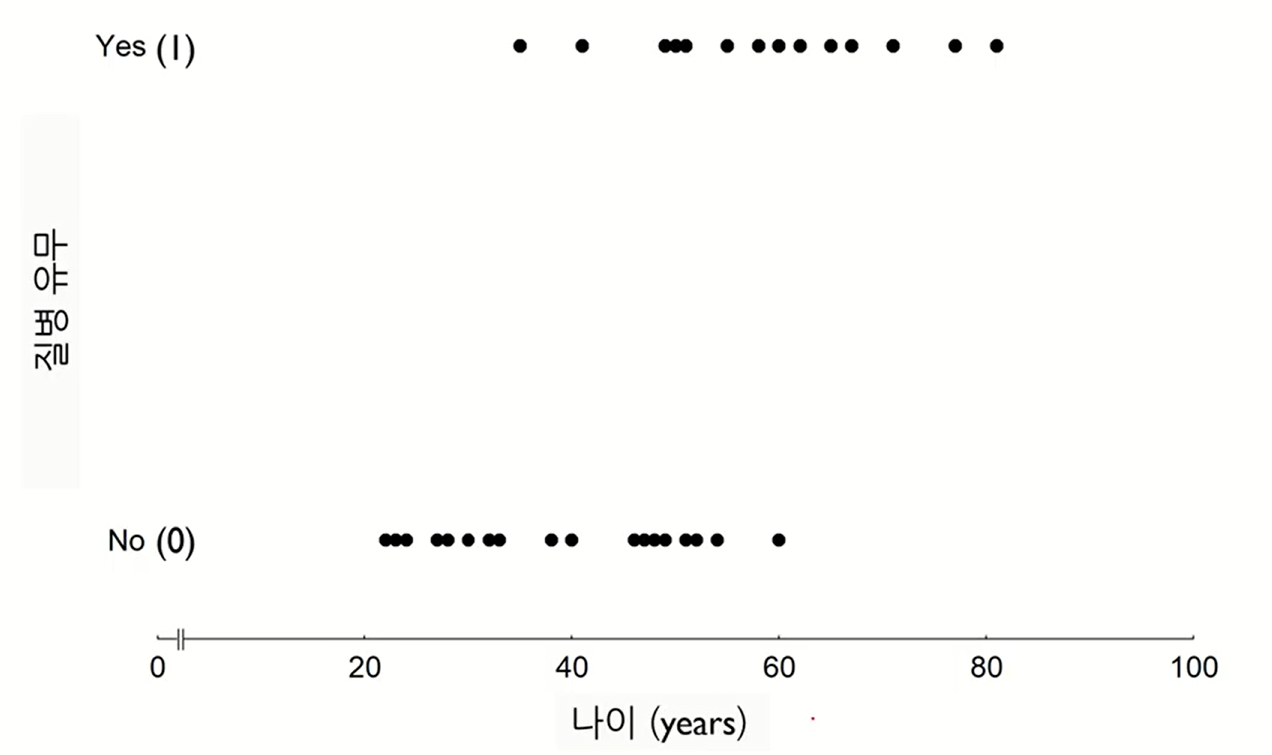
이를 선형 회귀를 이용해서 분류한다면 다음과 같은 직선을 통해 분류해야할 것이다.

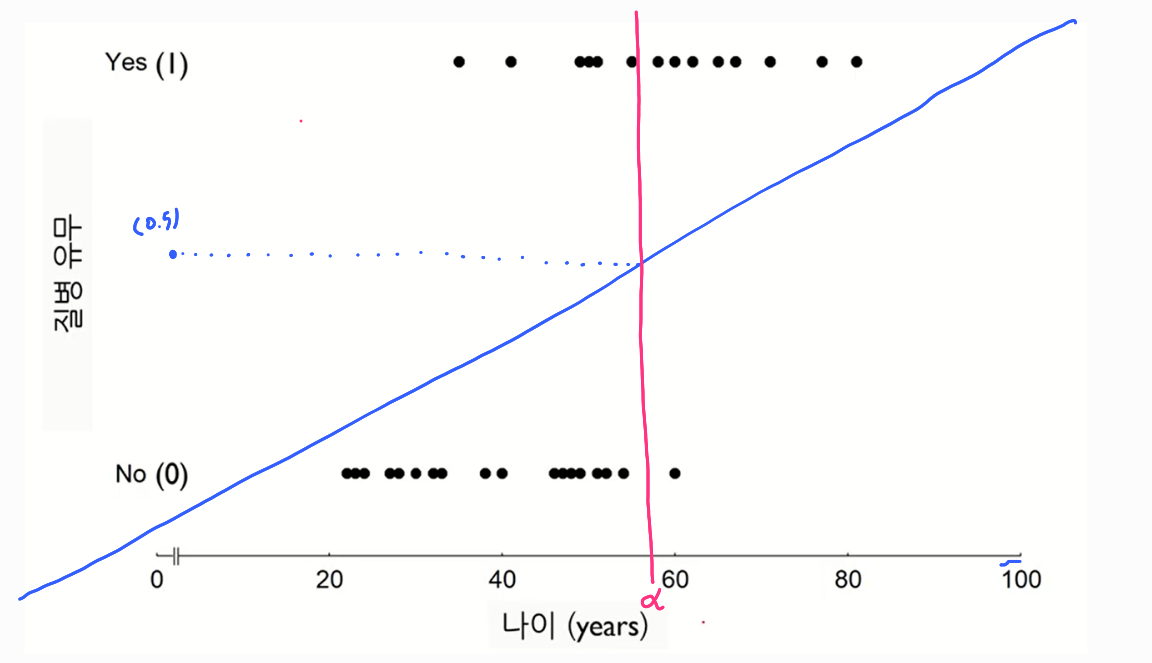
우리는 독립변수(나이) 에 따라서 독립변수(질병의 유무) 가 1인지 0인지를 유추할수있게 하는 모델을 찾아야 된다.
그렇다면 구한 선형 회귀 식에 나이를 대입하여 나온 값이 0.5를 넘으면 1, 넘지 않으면 0이라고 판단하는것이 합리적이다.
따라서 위의 그래프를 보게되면 나이가 $\alpha$ 일때를 기준으로 $\alpha$ 보다 작으면 0, $\alpha$ 보다 크면 1이라는 결론이 나오게된다. 하지만 이렇게 분류하는것은 적합해 보이지 않는다.(classification)

위의 데이터를 확률값으로 바꾸면 다음과 같다.

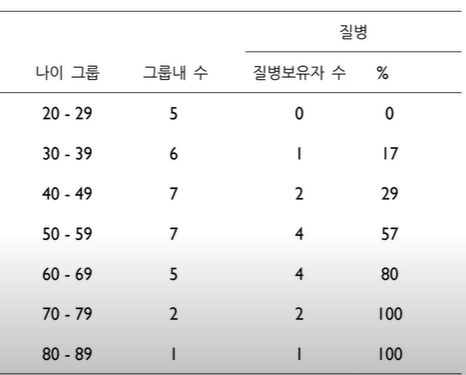
그리고 이 데이터를 2차원에 plot한 그림은 다음과 같다.

plot된 점들을 이어보면 s자 커브인것을 알 수 있을것이다. 이러한 s커브를 나탈낼수 있는 함수를 sigmoid함수라고 한다.
즉, 로지스틱 회귀란 독립변수를 input값으로 받아 종속변수가 1이 될 확률을 결과값으로 하는 sigmoid함수를 찾는 과정이다.

sigmoid 함수

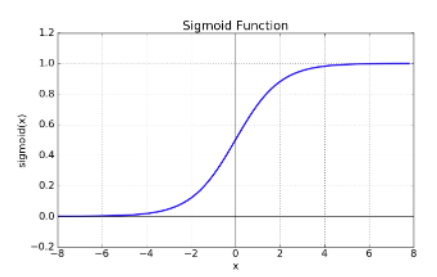
시그모이드 함수의 특징:

• $-\infty$ $<$ $x$ $<$ $\infty$
• $0$ $\leq$ $y$ $\leq$ $1$
• $sigmoid(x)=\displaystyle\frac{1}{1+e^{-x}} = \frac{e^x}{1+e^{x}}$
• $\displaystyle\frac{dsigmoid(x)}{dx} = sigmoid(x)(1-sigmoid(x))$

로짓 변환(Logit Transform) - 로지스틱 모델의 파라미터 해석

로짓 변환을 알기 위해서는 먼저 승산(Odds)이라는 개념을 알아야한다.
승산(Odds) = 성공 확률을 p로 정의할 때, 실패 대비 성공 확률 비율

$Odds$ = $\displaystyle\frac{p}{1-p}$

로지스틱 회귀 모델에서(이진 분류일때)의 Odds

$Odds$ = $\displaystyle\frac{1일 확률}{1-(1이 아닐 확률)}$ = $\displaystyle\frac{1일 확률}{0일 확률}$

로지스틱 모델은 해당 데이터의 최적의 sigmoid함수를 찾아가는 과정이라고 했다. 만약 독립변수가 하나(ex:나이), 종속변수가 하나(ex:질병의 유무) 인 데이터에 대한 sigmoid함수는 다음과 같은것이다.

$sigmoid(x) = \displaystyle\frac{1}{1+e^{-(\beta_0+\beta_1x)}}$
$Odds$ = $\displaystyle\frac{1/1+e^{-(\beta_0+\beta_1x)}}{1 - 1/1+e^{-(\beta_0+\beta_1x)}}$

위의 $Odds$ 에 $log$ 함수를 적용한것을 로짓변환이라고 한다.

$log(Odds) = log(\displaystyle\frac{1/1+e^{-(\beta_0+\beta_1x)}}{1 - 1/1+e^{-(\beta_0+\beta_1x)}}) = \beta_0 + \beta_1x$

로짓변환을 하는이유:

$sigmoid$함수에서는 $\beta_1$의 직관적인 해석이 불가능하다 하지만 로짓변환을 하게 되면 $\beta_0 + \beta_1x$ 의 형태가 되 해석할수 있는 상태가 된다.

로짓변환을 하고난 후 $\beta_0 + \beta_1x$ 일때 파라미터($\beta_1$)의 해석은 다음과 같다.

$\beta_1$의 해석 : x가 한단위 증가 했을 때 $log(Odds)$의 증가량

로지스틱 회귀 모델의 학습

로지스틱 회귀모델은 파라미터($\beta_0,\beta_1,\beta_2,...$)를 학습하기 위해 최대 우도 추정법(Maximum Likelihood Estimation)을 사용한다.
최대 우도 추정법이란 Likelihood Function을 최대로 하는 파라미터($\beta_0,\beta_1,\beta_2,...$)를 찾는것이다.

Likelihood Function:

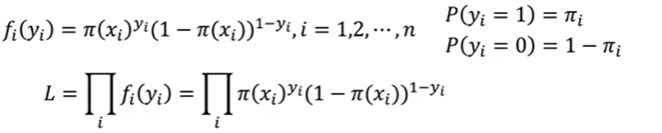
y값이 1이면 class1일 확률을 곱해주고 0이면 class0일 확률을 곱해주는것
즉, likelihood function을 최대화하는것이 1이 1로 분류될 확률, 0이 0으로 분류될 확률을 크게 해준다는 의미이다.

결국 Likelihood Function 은 비선형 함수 이므로 비선형 최적화이다 따라서 log를 취해준 Log-likelihood Function을 사용하면 최적화 문제를 풀기 더 쉬워진다.

Log-likelihood Function:

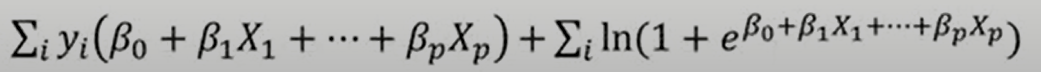
Likelihood함수에 log를 취한것

로지스틱 회귀 모델의 해석:

1.회귀 계수:
회귀 계수란 회귀 모델의 파라미터 ($\beta_0,\beta_1,\beta_2,...$)를 말하며 회귀 계수를 다음과 같이 해석할 수 있다.

회귀 계수가 양수이다. -> 해당 회귀계수에 해당하는 독립변수가 증가하면 성공할 확률이 증가한다.
회귀 계수가 음수이다. -> 해당 회귀계수에 해당하는 독립변수가 증가하면 성공할 확률이 떨어진다.

2.승산 비율(Odds ratio)

승산비란 나머지 입력변수는 모두 고정시킨 상태에서 한 변수를 1단위 증가시켰을 때 변화하는 Odds의 비율이다.

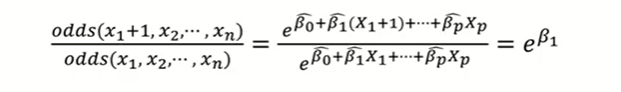
$X_1$이 1단위 증가하면 성공에 대한 승산비가 $e^{\beta_1}$만큼 변하게 된다.
$Odds Ratio$가 1보다 크다 = $e^{\beta_i}$가 1보다 크다 = $\beta_0$가 0보다 크다(즉, 회귀 계수가 양수)
$Odds Ratio$가 1보다 작다 = $e^{\beta_i}$가 1보다 작다 = $\beta_0$가 0보다 크다(즉, 회귀 계수가 음수)