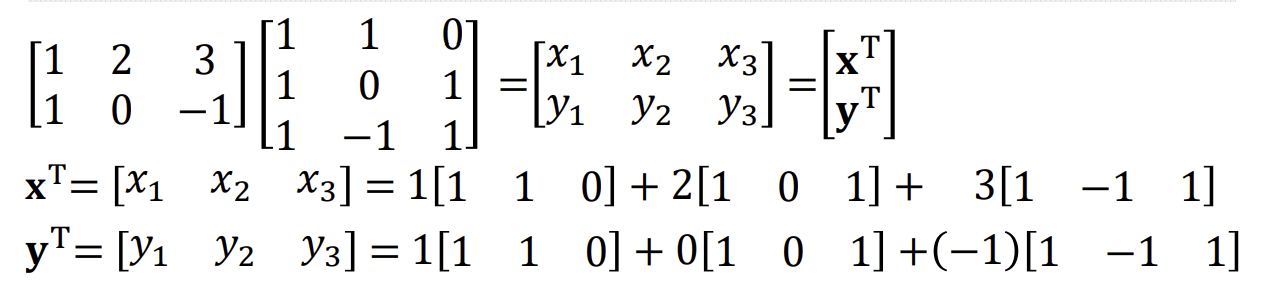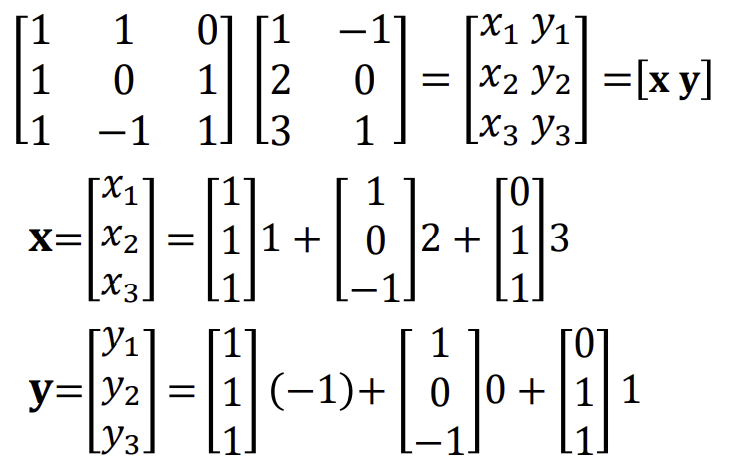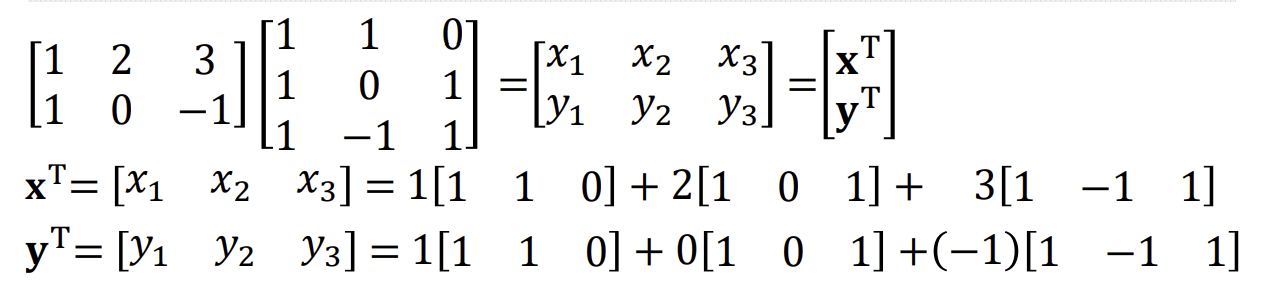행렬의 곲(Matrix Multiplication)은 선형 결합(Linear Combinations)이다.

선형 결합

$n$차원 공간의 벡터($v_1, v_2, v_3, ......v_n$) 과 스칼라 ($c_1, c_2, ...c_p$) 가 있을 때

를 벡터($v_1, v_2, v_3, ......v_n$)의 선형결합이라 한다.(이때 $c$는 0을 포함한 실수이다.)

선형 결합의 이용

행렬 방정식$Ax = b$를 선형 결합을 이용하여 나타낼 수 있다.

선형 결합을 이용한 방정식의 해는 b가 Span($a_1, a_2, a_3$) 안에 있어야 존재한다.

Span설명:https://velog.io/@skkumin/Span%EC%83%9D%EC%84%B1

행렬의 곲을 선형결합으로 표현하기

두행렬 $A, B$가 있을때 행렬의 곲 $AB$는 열벡터와 행벡터의 선형 결합으로 표현할 수 있다.

1. 왼쪽 행렬$A$의 열벡터의 선형결합
2. 오른쪽 행렬$B$의 행벡터의 선형결합

• 열벡터의 선형 결합으로 표현하기
  

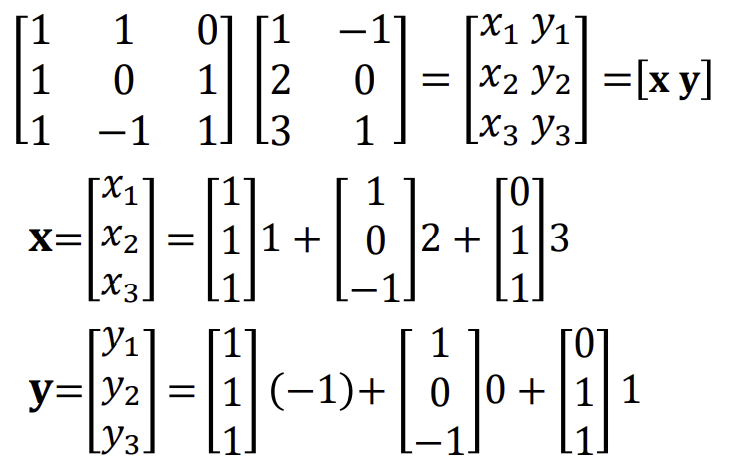
• 행벡터의 선형 결합으로 표현하기