styleGAN : 고화질 이미지 생성에 적합한 아키텍쳐 제안
- PGGAN 베이스라인 아키텍처의 성능을 향상시킴
- style transfer에서 아이디어를 얻음
- Discriminator와 loss function은 수정하지 x
- Disentanglement 특성을 향상시킴
- 고해상도 얼굴 데이터셋(FFHQ)를 발표함
PGGAN
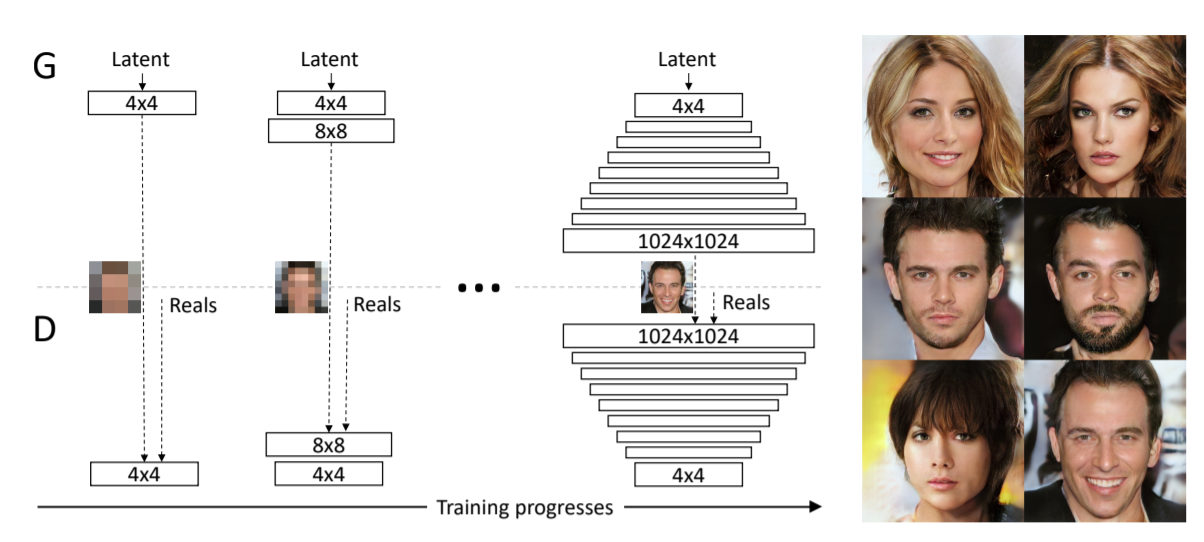
- 학습 과정에서 레이어를 추가(점차 해상도를 높힘) → 고해상도 이미지 학습 성공
- 생성자(Generator)와 판별자(Discriminator)가 정확히 대칭
- 한계점 : 이미지의 특징 제어가 어려움 (다양한 특징들이 분류되어 있지 않아서)
⇒ styleGAN에서 이를 개선!
StyleGAN
- Mapping network
: 가우시안 분포에서 샘플링한 z벡터를 사용하지 x, FC(fully convolutional)를 거쳐 만들어진 w 벡터를 사용! (상대적으로 특정분포를 따라야하는 제약이 사라지기 때문에 더 linear한 space에서 특징들이 분류되는 형태로 학습 가능).
- AdaIN
: 다른 데이터로부터 스타일 정보를 가져올 수 있음.

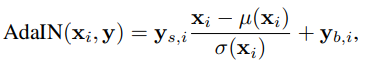
x_i = feature map이고 이를 normalization
여기에 style y의 scaling과 bias 적용
- Affine transformer : w는 512개로 AdaIN을 적용하기엔 채널 개수와 사이즈가 다르기 때문에 이곳에서 아핀 변환(affine transformation)을 적용 → 1024차원(y가 scale, bias 두개로 들어가서)
- 학습시킬 파라미터가 필요하지 x (감마(r)와 베타(B)를 사용하지 않음) → style의 scale과 bias를 사용하기 때문에
- 생성자 네트워크(Synthesis Network) : 9개의 블록(각각 2개의 Convolution Layer, 2개의 AdaIN Layer로 구성)
- 다양한 style에 대한 정보가 layer를 거치는 과정에서 적용될 수 있게 하여 스타일 정보에 의해 이미지 다양성이 보장됨
- 초기 입력을 상수로 대체
(Synthesis Network의 첫번째가 const 4x4x512임) → 경험적으로 성능이 향상됨
(이전에 생성자에 latent vector를 넣을 땐 latent vector에 따라 다양한 이미지가 생성될 수 있도록 했는데, 본 논문에서는 별도의 style 정보를 layer를 거칠 때마다 따로 넣어주기 때문에 굳이 맨처음에 latent code로부터 시작하지 않아도 됨)
- stochastic variation(확률적 측면)
: 주근깨, 머리카락의 배치 등
한 사람의 이미지를 여러번 찍었다고 해도, 바람의 세기에 따라 머리카락의 배치가 조금씩 달라지거나 컨디션에 따라 여드름이나 주근깨 등 다양한 확률적인 feature가 개입될 수 있음
→ 별도의 Noise를 입력으로 넣어서 각각의 layer마다 Noise벡터가 들어가게 함
-Coarse noise : 큰 크기의 머리 곱슬거림, 배경 등
-Fine noise : 세밀한 머리 곱슬거림, 배경 등
⇒이를 통해 더욱 세세한 부분을 바꿀수 있어 사실적인 이미지를 다양하게 생성할 수 있다.

a는 noise를 모든 layer에 적용한 것
b는 noise를 적용 안한 것
c는 64x64~1024x1024 레이어(fine layer)에만 노이즈를 적용한 것
d는 4x4~32x32 layer(coarse layer)에만 노이즈를 적용한 것
→ a가 가장 잘 만들어짐을 확인할 수 있다.
StyleGAN의 생성자는 더욱 linear하며 덜 entangled되어 있다.
- Style Mixing(Mixing Regularization)
: 인접한 레이어 간의 스타일 상관관계를 줄인다.
1. 두개의 입력 벡터를 준비
2. 크로스오버 포인트를 설정
3. 크로스오버 이전은 w_1, 이후는 w_2를 사용
스타일은 각 레이어에 대해 지역화된다.

→ 각각의 style 정보가 입력되는 layer의 위치에 따라 해당 style이 미치는 영향의 크기가 달라질 수 있다.
- Coarse styles : 얼굴형, 얼굴 포즈, 안경 유/무 등 전반적인 큼지막한 정보
- Middle styles : 헤어스타일, 눈을 떴는지 감았는지 등 좀 더 세밀한 정보
- Fine styles : 색상적인 측면, 세밀한 구조같이 훨씬 더 세밀한 정보를 컨트롤
- Disentanglement 관련 성능 측정 지표
1. Path Length
: 두 벡터를 보간(interpolation)할 때 얼마나 급격하게 이미지 특징이 바뀌는지

slerp : 구면 선형 보간 / learp : 선형 보간
1-1. z1와 z2를 뽑아서 interpolation 진행, 바로 옆 지점에서도 interpolation 진행
1-2. 각각 지점의 결과 이미지를 만들어냄
1-3. 사전 학습된 VGG에 넣어서 feature 간의 거리가 얼마나 먼지 측정
→ 거리가 클수록 interpolation이 제대로 안되고 있다=entanglement하다
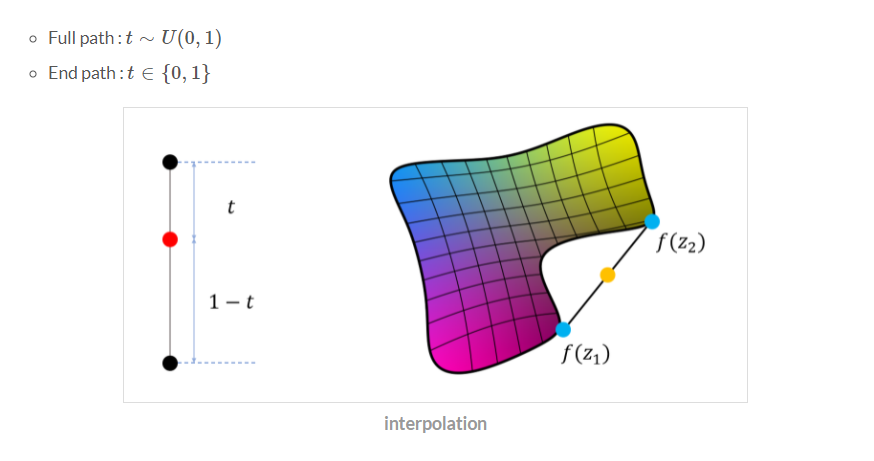
z - slerp(z가 가우시안분포를 따르기 때문에) : t는 0과 1사이의 유니폼 분포를 따릅니다.
w - lerp(이미 mapping function을 거친 W는 normalized 된 상태가 아니기 때문에) : t가 0 또는 1의 값으로 고정합니다. 그냥 똑같이 유니폼 분포를 따르게 한다면 아래 오른쪽 그림의 노란색 원처럼 실제 존재하지 않는 벡터 부분이 interpolation 됩니다. 이러면 W에서 구한 path가 아무래도 Z에서 구한 path보다는 더 불리한 수치가 나오기 마련입니다. 따라서 0 또는 1의 값으로 w 근처의 값만 가지고 계산
2. Separability
: latent space에서 attributes(속성)가 얼마나 선형적으로 분류될 수 있는지 평가
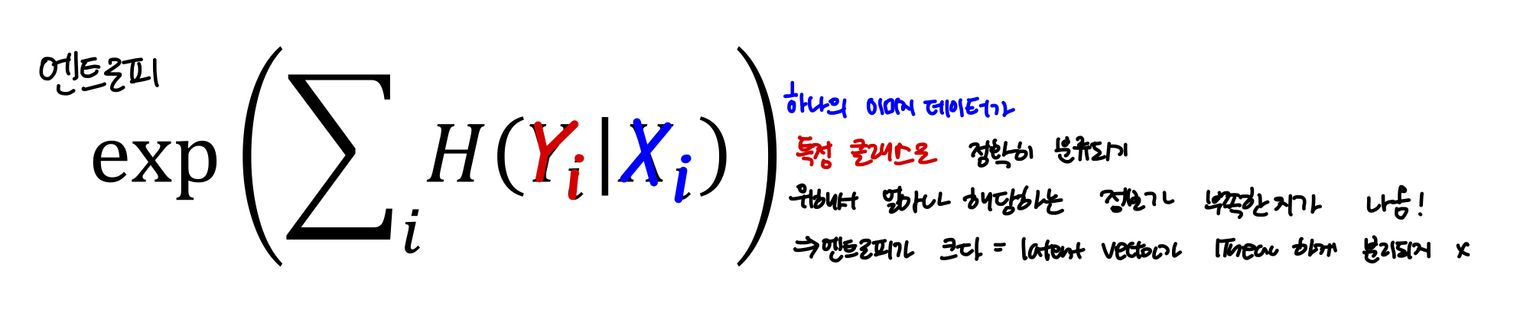
Entropy란?
:무작위성으로 볼 수 있음
랜덤 변수 x의 값이 예측가능하면 엔트로피가 낮음 / 예측하기 어렵다면 엔트로피는 높음
2-1. CelebA-HQ라는 얼굴마다 성별 등의 40 개의 binary attributes가 명시되어있는 데이터셋을 이용하여 40개의 분류 모델을 학습시킴.
2-2. 하나의 속성마다 20만개의 이미지를 생성하여 분류 모델에 넣는다.
2-3. 분류모델에서 confidence가 낮은 절반은 제거하여 10만개의 레이블이 명시된 latent vector를 생성한다. 즉, 높은 confidence를 가진 잘 만들어진 이미지만 남겨놓음
2-4. 이를 새로운 데이터셋으로 활용한다.(성별 등의 40개의 binary 속성에 대한 label 값이 포함된 데이터셋)
2-5. 이 데이터 셋에서 각각의 attributes 마다 linear SVM 모델을 학습하고 이 모델에서 엔트로피를 계산한다.
⇒ 측정 결과 = w space가 z보다 이상적인 성질을 가짐
+) Truncation trick in W
실제 학습 데이터의 분포를 고려하면, 밀도(density)가 낮은 부분의 경우 불안정한 학습이 된다. 이를 방지하기 위해 쓰는 방법이 truncation trick이다.
상대적으로 low density 영역에서 Sampling을 진행하면 덜 그럴싸한 이미지가 나올 확률이 높아지기 때문에 평균 latent vector에 가까워질수 있도록해서(=trucation) 보다 그럴싸한 이미지를 만들수 있도록함 ! = W의 중간값을 구해 중간값에 가까울수 있도록 잘라내겠다!
ψ는 0~1 사이 값으로 설정하고 1이면 truncation trick 사용하지 않는 결과랑 동일하고 0이면 평균적인 결과물이 나온다.
용어
- entangle
서로 얽혀 있는 상태여서 특징 구분이 어려운 상태. 즉, 각 특징들이 서로 얽혀있어서 구분이 안됨- disentangle
각 style들이 잘 구분 되어있는 상태여서 어느 방향으로 가면 A라는 특징이 변하고 B라는 특징이 변하게 되어서 특징들이 잘 분리가 되어있다는 의미.
선형적으로 변수를 변경했을 때 어떤 결과물의 feature인지 예측할 수 있는 상태.

