데이터베이스 인덱스

smc2315·2024년 3월 13일

목록 보기

3/4

1. 인덱스

1-1. 인덱스란?

인덱스는 데이터베이스에서 테이블에 대한 동작의 속도를 높여주는 자료 구조이다. 인덱스를 책의 맨 끝에 있는 "찾아보기"로 비유할 수 있다. 책에서는 맨 뒤에 존재하는 "찾아보기"를 활용하여 원하는 정보에 쉽게 접근할 수 있다. DBMS도 데이터베이스 테이블의 모든 데이터를 검색해서 원하는 결과를 가져오기에는 시간이 오래 걸리기 때문에 칼럼의 값과 해당 레코드가 저장된 주소를 키와 값의 쌍으로 삼아 인덱스를 만들어 둘 수 있다.

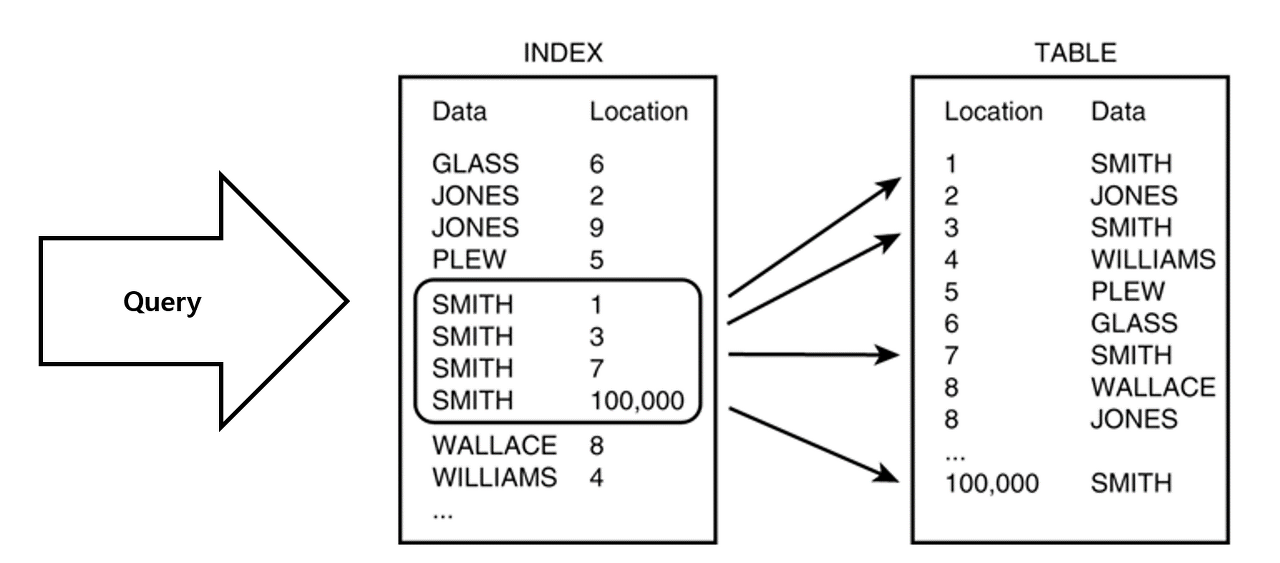
1-2. 인덱스의 장단점

장점

인덱스의 가장 큰 특징은 데이터들이 정렬이 되어있다는 점이다. 인덱스를 사용하는 경우 다음과 같이 데이터가 정렬되어 있으면 효율성이 증가하는 경우에 장점을 발휘한다.

조건 검색 WHERE 절의 효율성
정렬 ORDER BY 절의 효율성
MIN, MAX의 효율적인 처리가 가능

단점

인덱스의 가장 큰 문제점은 정렬된 상태를 계속 유지시켜줘야 한다는 점이다. 이 때문에 레코드 내에 데이터 값이 바뀌는 부분이라면 악영향을 미친다.

INSERT, UPDATE, DELETE를 통해 데이터가 추가되거나 값이 바뀐다면 인덱스 테이블 내에 있는 값들을 다시 정렬을 해야 한다.
인덱스는 테이블의 전체 데이터 중에서 10~15% 이하의 데이터를 처리하는 경우에만 효율적이고 그 이상의 데이터를 처리할 땐 인덱스를 사용하지 않는 것이 더 낫다.
인덱스를 관리하기 위해서는 데이터베이스의 약 10%에 해당하는 저장공간이 추가로 필요하다.

1-3. 인덱스의 관리

인덱스는 항상 최신의 데이터를 정렬된 상태로 유지해야 원하는 값을 빠르게 탐색할 수 있다. 그렇기 때문에 인덱스가 적용된 컬럼에 INSERT, UPDATE, DELETE가 수행된다면 계속 정렬을 해주어야 하고 그에 따른 부하가 발생한다. 이런 부하를 최소화하기 위해 인덱스는 데이터를 삭제하는 대신 삭제 마크 처리만 한다.

INSERT : 새로운 데이터에 대한 인덱스를 추가한다.
DELETE : 삭제하는 데이터의 인덱스를 사용하지 않는다는 작업을 진행한다.
UPDATE : 기존의 인덱스를 사용하지 않음 처리하고, 갱신된 데이터에 대해 인덱스를 추가한다.

1-4. 인덱스를 쓰면 좋은 경우

다음과 같은 경우에 인덱스를 활용하는 것이 좋다.

규모가 작지 않은 테이블
DML(INSERT, UPDATE, DELETE) 작업이 자주 발생하지 않는 컬럼
JOIN이나 WHERE 또는 ORDER BY에 자주 사용되는 컬럼
카디날리티(cardinality)가 높은(중복도가 낮은) 컬럼

2. 인덱스의 자료구조

인덱스를 구현하는 자료구조는 대표적으로 해시 테이블, B-Tree, B+Tree 등이 있다. 각 자료구조를 하나씩 살펴보자.

2-1. 해시 테이블

해시 테이블은 Key-Value 쌍으로 데이터를 저장하는 자료구조이다. 데이터의 Key를 알고 있으면, 데이터에 O(1)의 시간 복잡도로 접근할 수 있다.

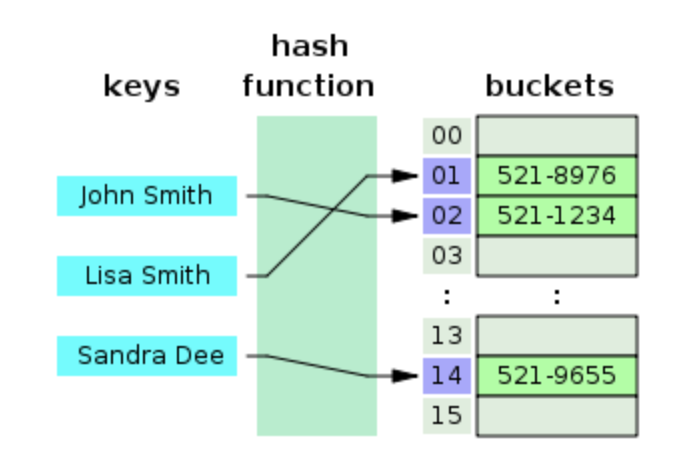
하지만, 해시 테이블은 부등호 연산에 부적합하기 때문에 실제로 DBMS의 인덱스로는 많이 쓰이지 않는다. 해시 테이블의 데이터는 정렬되어 있지 않으므로, 부등호 연산이 많이 발생하는 데이터베이스에서는 적합하지 않다.

2-2. B-Tree

B-Tree는 Balanced Tree의 약자로 이름에서도 알 수 있듯이 일반적인 트리와는 달리 언제나 같은 높이를 유지하는 균형된 트리를 유지하여 검색 성능을 유지시킬 수 있다.

B-Tree의 핵심은 데이터가 정렬된 상태로 유지되어 있다는 것이다.

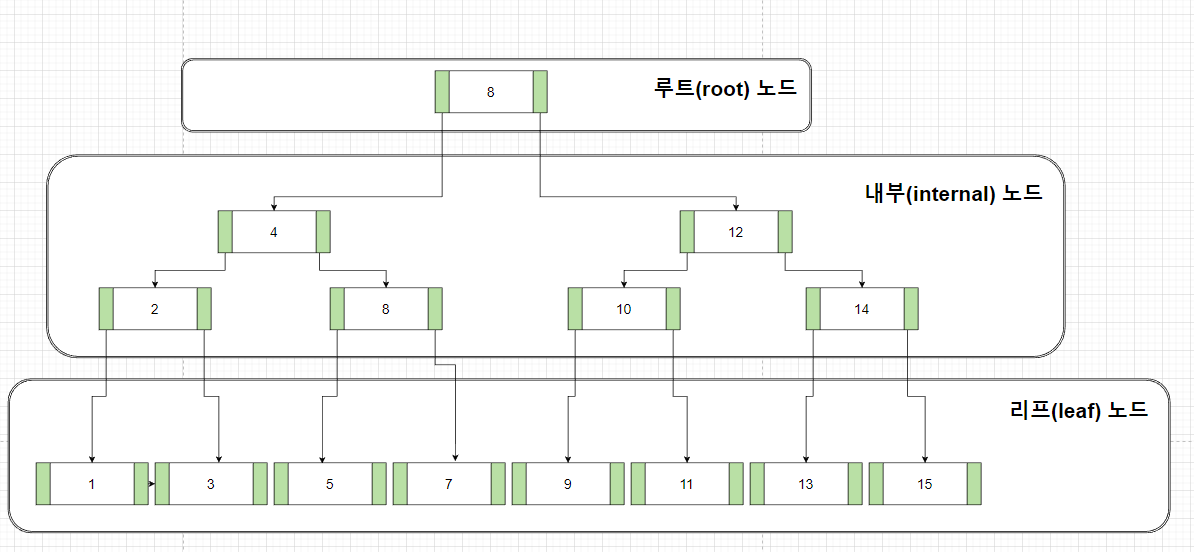
루트(root) 노드
최상단에 위치한 노드
리프(leaf) 노드
자식이 없는 최하단에 위치한 노드
내부(internal) 노드
루트노드와 리프노드를 제외한 모든 노드

B-tree는 Binary search tree와 유사하지만, 한 노드 당 자식 노드가 2개 이상 가능하다. key 값을 이용해 찾고자 하는 데이터를 트리 구조를 이용해 찾는 것이다.

B-Tree는 최상위에 루트 노드가 존재하고 중간노드인 브랜치 노드를 거쳐 가장 하위에 리프 노드가 존재한다.

B-Tree는 어떤 값에 대해서도 같은 시간에 결과를 얻을 수 있다. 즉, 균일성을 가지고 있다.
B-Tree 처음 생성 당시는 균형 트리이지만 테이블 갱신(INSERT/UPDATE/DELETE)의 반복을 통해 서서히 균형이 깨지고, 성능도 악화된다. 어느 정도 자동으로 균형을 회복하는 기능이 있지만, 갱신 빈도가 높은 테이블에 작성되는 인덱스 같은 경우 인덱스 재구성을 해서 트리의 균형을 되찾는 작업이 필요하다.

2-3. B+Tree

B+Tree는 B-Tree의 확장된 개념으로 MySQL의 InnoDB에서 사용된다.

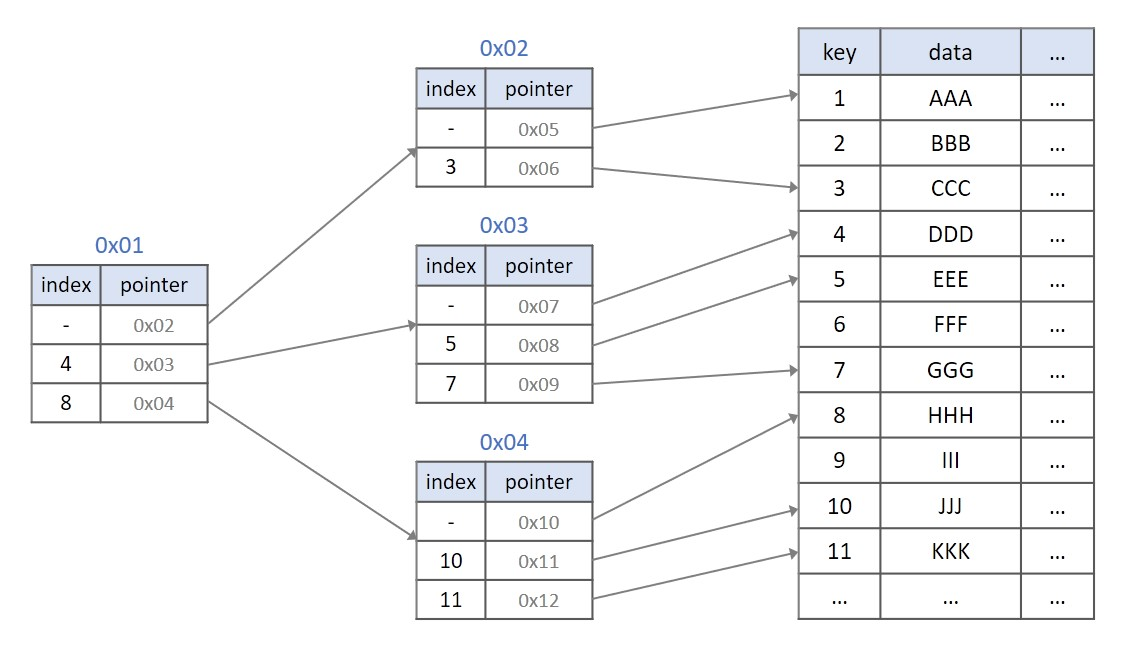
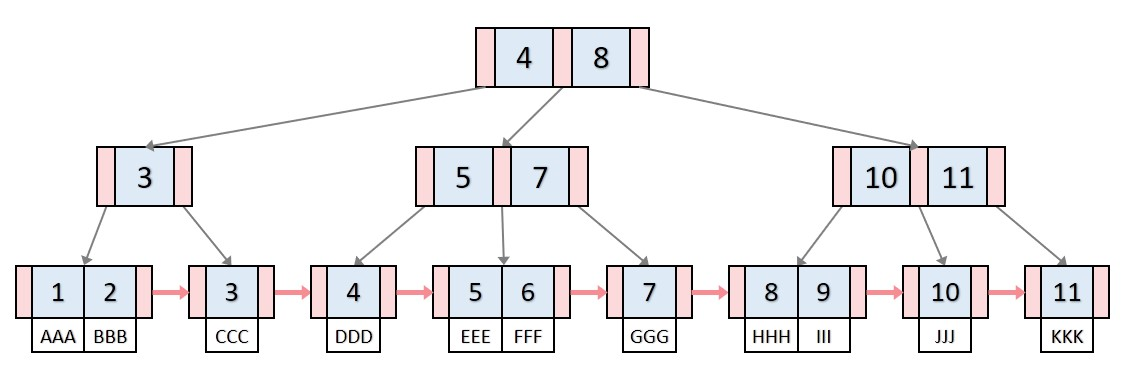
B+Tree는 다음과 같은 특징을 가지고 있다.

모든 key, data가 리프노드에 모여있다. B트리는 리프노드가 아닌 각자 key마다 data를 가진다면, B+트리는 리프 노드에 모든 data를 가진다.
모든 리프노드가 연결리스트의 형태를 띄고 있다. B+트리는 리프노드에서 선형검사를 수행할 수 있어 시간복잡도가 굉장히 줄어든다.
리프노드의 부모 key는 리프노드의 첫번째 key보다 작거나 같다.