스트라이드는 필터가 입력 이미지를 가로지르며 이동하는 스텝 사이즈를 나타내며,
출력 특징 맵의 크기와 연산 효율성을 조절하는 중요한 파라미터이고,
Stride = 스텝 사이즈 로 보여진다.
Stride는 번역하면 "~을 성큼 넘어서다"
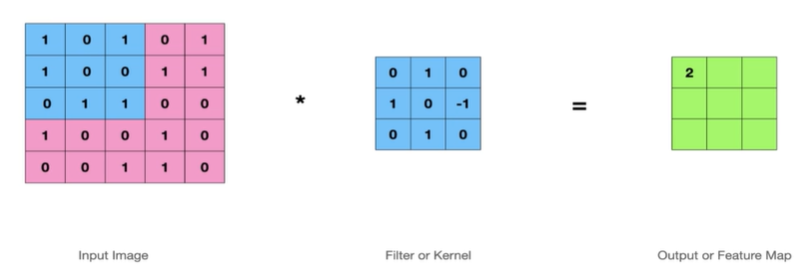
Stride = 1 일때,
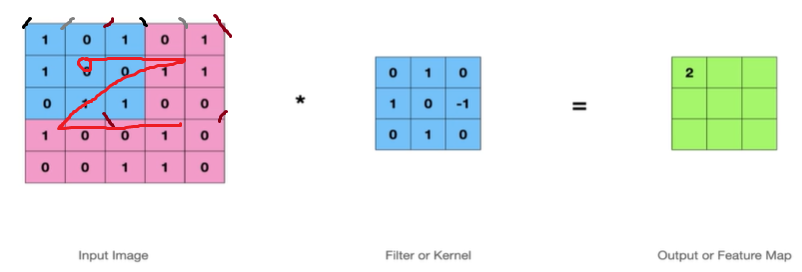
한칸씩 이동하면서 연산을 하며 기능맵을 만들어낸다.
Stride = 2 일때는 말그대로 2칸씩 넘어가게 된다.
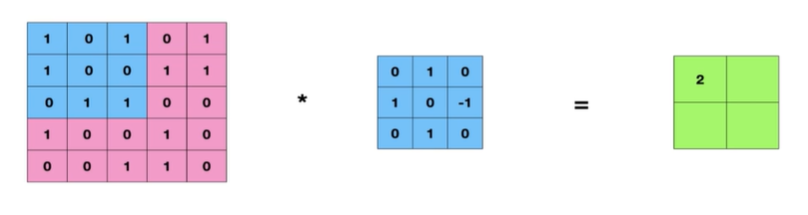
오른쪽으로 2칸 이동해서 연산
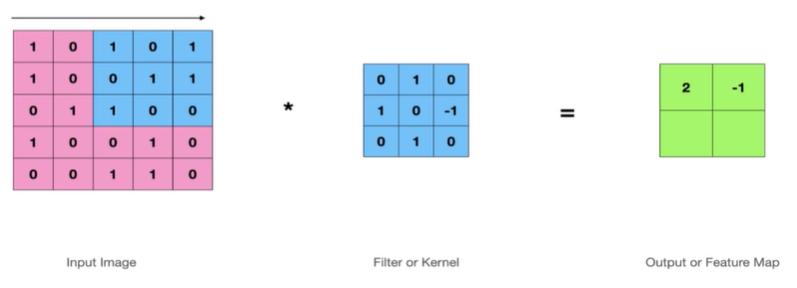
에지 연산이 끝났으므로 아래로 2칸 내려와서 연산
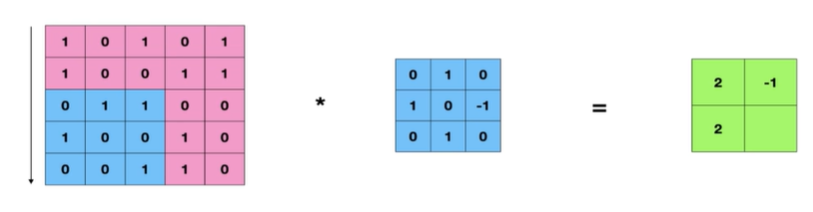
다시 두칸 이동해서 연산
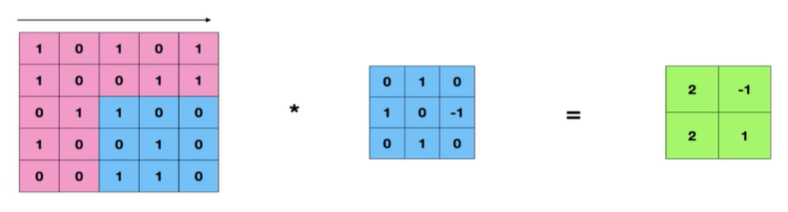
이처럼 Stride는 연산을 할때 몇 칸 이동하면서 연산할지에 대한 숫자, 즉 스텝 사이즈를 나타낸다.
여기서 기능 맵이나 출력 크기가 작아진 걸 확인 할 수 있다.
즉 큰 보폭(stride 값이 큰)으로 이동할수록 output, 기능맵의 크기가 줄어든다.
stride = 1, 2의 결과를 보았을때 Stride를 사용하면 아래 3가지를 알수있다.
- 스트라이드가 클수록 피쳐 맵 출력이 작아진다.
- 스트라이드가 클수록 겹침이 적음(여러번 사용되는 픽셀의 수가 줄어듬)
- 스트라이드를 사용하여 피쳐 맵 출력의 크기를 제어할 수 있다.
여기서 3번이 중요한데 왜 중요할까?
Big Network(딥러닝 모델)에서 출력의 크기를 조절할 수 있다는것은
연산 효율성을 높이고, 메모리 사용량을 줄이며, 특징 맵의 크기를
효과적으로 조절하는 데 중요한 역할을 한다.
효율적인 부분도 있고,
핵심은 스트라이드의 크기를 조절하여 네트워크가 입력 이미지의
다양한 특징을 효과적으로 학습할 수 있도록 설계하는 것이다.
Calculating Output Size
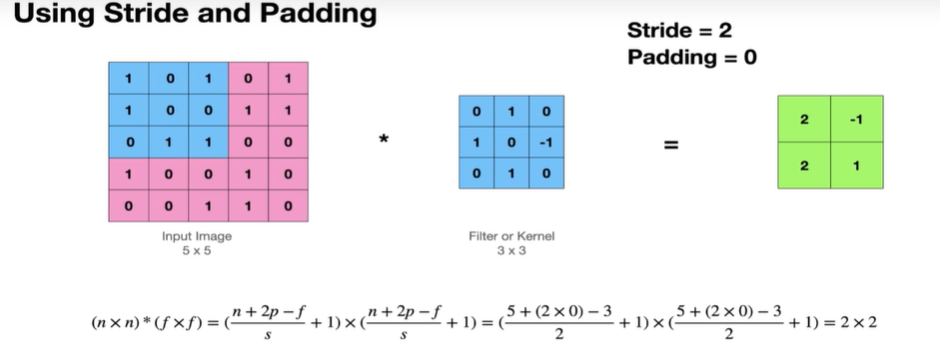
Stride, Padding에 대해서 알았으니 연산에 대해서도 확인해보면
위의 이미지는 Stride =2, Padding(입력이미지를 둘러싸서 에지데이터를 여러번 학습시키기 위함, 입력 크기 보존) = 0 일때의 출력 사이즈를 계산한것이다.
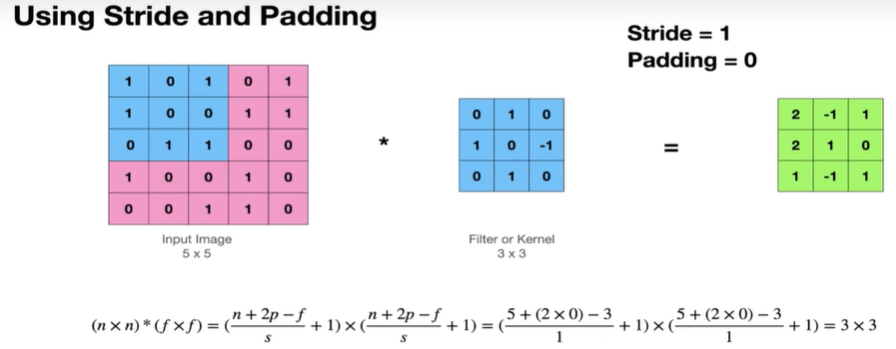
Stride = 1 , Padding = 0일때, 스트라이드가 작아졌으니 출력의 크기가 증가할것을 알면된다.
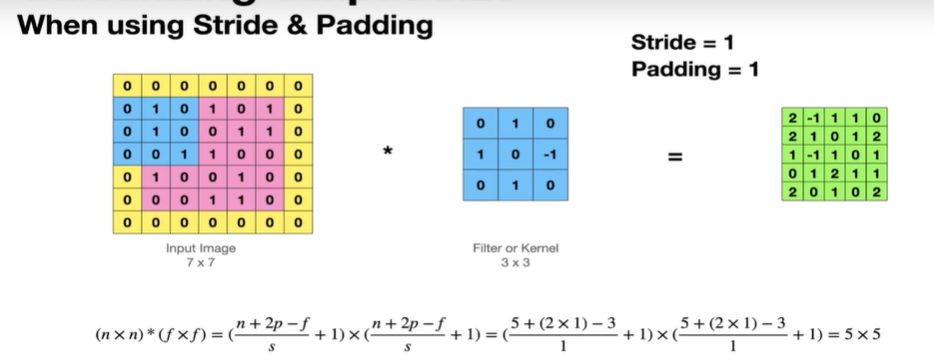
padding = 1일때, 출력의 크기가 보존되고, 패딩의 크기가 커질수록 더 큰 기능맵이 나온다.
우리가 아는 뉴럴네트워크나 CNN의 경우 stride, padding = 1로 Pooling 한다.
이렇게만 확인하기엔 이해하기 힘드니까 하나의 흐름을 확인해보자.
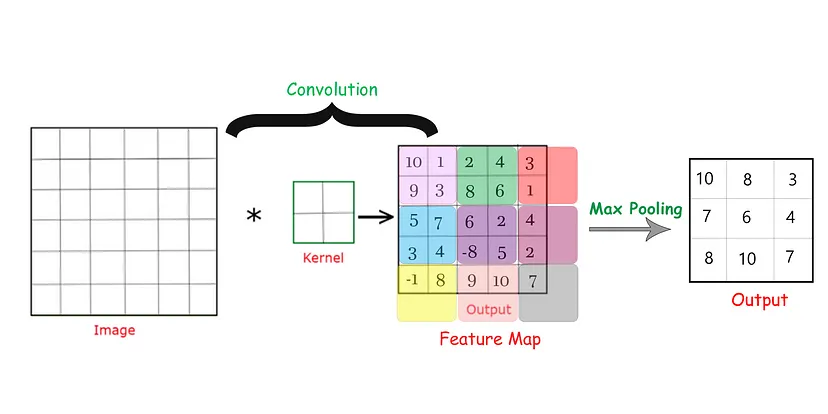
최대 풀링 과정
여기 위의 이미지는 합성곱 신경망(CNN)의 컨볼루션 및 최대 풀링(Max Pooling) 과정을 시각적으로 설명한 것이다.
필터를 이미지에 적용하여 컨볼루션 연산으로 특징 맵(Feature Map) 을 만들었고,
원본 이미지 크기: 7x7
커널 크기: 3x3
컨볼루션 연산 후
출력 특징 맵 크기: 5x5
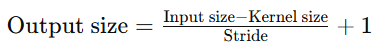
아래 공식을 계산해 Stride = 1인것을 알수있다.
한칸씩 이동하면서 컨볼루션 연산을 했다는것이다.
그리고 Max pooling을 할때, Feature Map에서 2x2씩 색칠을 한것을 확인할 수 있다.
특징 맵에서 2x2 크기의 창을 사용하여 최대 풀링으로
겹치지 않고 한번에 2칸씩 이동하는 스트라이드 2를 사용해 새로운 Feature Map을
만들어낸 과정이다.
이론은 이해가 됐지만, 실제로 어떻게 사용하는지 확인을 하면서
습득을 하는것이 중요해 보인다.