[Paper Review] DCN

본 글은 2017년 발표된 Deep & Cross Network for Ad Click Predictions을 읽고 요약 및 정리한 글입니다.
논문
직접 구현 DCN 모델 코드 (Pytorch)
직접 구현 DCN Movielens100k 학습 코드 (Jupyter)

---

0. Summary

• Wide & Deep vs DeepFM VS DCN

항목	Wide & Deep	DeepFM	DCN
구성	Wide (Linear model) + Deep (MLP)	FM (low-order interactions) + Deep (high-order interactions)	Cross Network(feature crossing) + Deep (MLP)
Feature Engineering	수동 Feature Cross 필요	자동 Feature Factorization Machines 학습 (2차)	자동 Feature Cross 학습 (교차층으로 다양한 차수)
Embedding 공유	❌ (Wide와 Deep 입력 분리)	✅ (FM과 Deep이 Embedding Layer 공유)	✅ (Cross와 Deep이 Embedding을 공유)
Interaction Modeling	- Wide: 1차(선형), 수동 조합	- FM: 2차 pairwise interaction 자동 학습	- Cross: 입력과 이전층의 외적 기반 명시적 교차
모델 수식	$\hat{y} = \sigma(W_{wide}^T x + W_{deep}^T a^{(L)} + b)$	$\hat{y} = \sigma(\hat{y}_{FM} + \hat{y}_{Deep})$	$x^{(l+1)} = x^{(0)} (x^{(l)})^T w^{(l)} + b^{(l)} + x^{(l)}$ 최종: $\hat{y} = \sigma(W_{out}^T [x_{cross}^{(L)}; a^{(L)}_{deep}] + b)$

• DCN

구분	Cross Component	Deep Component
역할	저차원 명시적 feature crossing	고차원 비선형 관계 학습
목적	저차원 상호작용(feature cross) 자동 학습	고차원의 복잡한 비선형 표현 학습
특징	원본 입력과 이전층의 내적/외적을 통해 교차 특징 포착	비선형 특징 포착
모델 수식	$\mathbf{x_{l+1}} = \mathbf{x_0 x_l^T w_l + b_l + x_l}$	$a^{(l+1)} = \sigma(W^{(l)} a^{(l)} + b^{(l)})$ $\hat{y}_{deep} = \sigma(W_{out} a^{(L)} + b_{out})$

1. Introduction

• CTR Prediction은 광고 시장에서 중요
• Cross features는 모델의 표현력을 향상
  • 빈번하게 예상되는 피처
  • 사용되지 않은 피처
  • Large-scale에서 이를 파악하는게 어려움
    • manual feature engineering
    • exhaustive search
• DCN
  • NO manual feature engineering & exhaustive search
  • Cross network
    • feature cross를 명시적으로 적용
    • 네트워크 내부에서 자동으로 적용
  • DNN
    • Higher order interactions를 모델링

2. Deep & Cross Network(DCN)

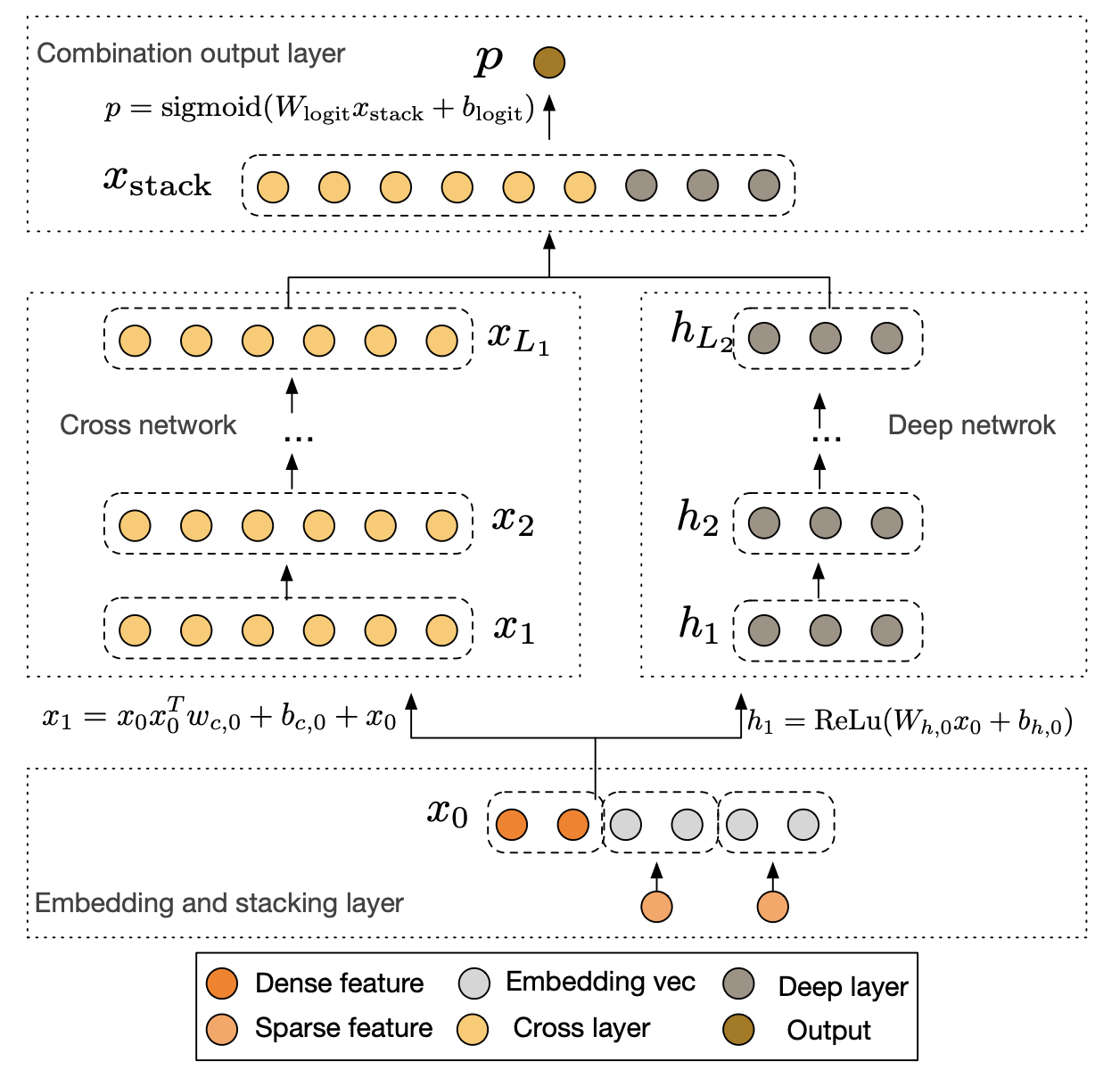
2-1. Embedding and Stacking Layer

• Web-scale에서는 주로 Sparse Categorical Feature 사용됨
  • Embedding Procedure
  • $\mathbf{x}_{embed, i}=W_{embed,i}\mathbf{x}_i$
• $\mathbf{x_0} = \left [ \mathbf{x^\top_{embed,1}}, ... ,\mathbf{x^\top_{embed,k}}, \mathbf{x^\top_{dense}} \right ]$

2-2. Cross Network

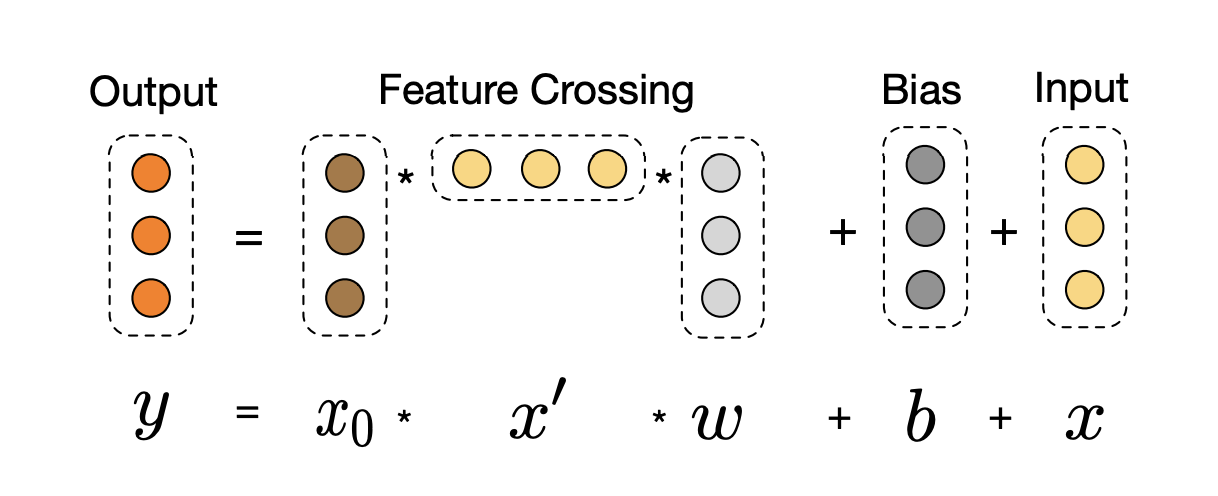
• cross layer
  • 효과적인 방법으로 명시적인 피처 cross를 적용
  • $\mathbf{x}_{l+1} = \mathbf{x}_0 \mathbf{x}^\top_l \mathbf{w}_l + \mathbf{b}_l + \mathbf{x}_l = f(\mathbf{x}_l,\mathbf{w}_l,\mathbf{b}_l)+\mathbf{x}_l$
    • Weight, Bias: ${\mathbf{w}_l, \mathbf{b}_l \in \mathbb{R}^d}$
    • Residual: $\mathbf{x_0}$를 각 layer마다 더함
• High-degree interaction
  • Layer depth에 따라 cross 차원이 증가
• Complexity Analysis
  • $L_c$: cross layer의 수
  • cross network의 parameter 수는 $d \times L_c \times 2$
  • time, space는 input dimension에 선형 비례
  • DNN에 비해 굉장히 작기 때문에 무시할 수 있는 크기

2-3. Deep Network

• DNN
  • $\mathbf{h}_{l+1} = f(W_l\mathbf{h}_l + \mathbf{b}_l)$
• Complexity Analysis
  • $d \times m + m + (m^2 + m) \times (L_d-1)$
  • $L_d$: deep layer의 수
  • $m$: deep layer의 size

2-4. Combination Layer

• Joint Train
  • cross network의 output
  • neep network의 output
  • sigmoid를 이용하여 학습
  • $p = sigmoid(W_{logit}x_{stack} + b_{logit})$
• Logloss를 이용해서 학습

3. Cross Network Analysis

3.1 Polynomial Approximation

• cross network
  • Weierstrass: 모든 연속 함수는 polynomial로 근사 가능
  • 실제 세상의 데이터를 더 잘 일반화하고 설명 가능
  • l-layer cross network를 이용하면 (l+1) degree인 polynomial까지 표현 가능
    • Parameter는 $O(d)$에 비례
    • 입력이 3차원(d=3)
    • cross layer는 2층
      • 입력 $x_0 = [x_1, x_2, x_3]$
      • 차수 1항: $x_1, x_2, x_3$
      • 차수 2항: $x_1x_2, x_1x_3, x_2x_3, x^2_1, x^2_2, x^2_3$
    • $x^{l+1} = x^0(x^l)^{\top}w^l + b^l + x^l$
  • 이와 같이 이전 층 $x^l$과 원 입력 $x^0$의 내적/외적 형식을 이용해서 교차항 자동 생성
  • Parameter: O(d) - 입력 차원에 비례

3.2 Generalization of FMs

• FM의 장점
  • Parameter sharing
    • 효율성(Efficient): 추천 시스템의 sparse feature에 대한 특성
    • 일반화(Generalization): unseen or rarely seen feature interactions
• DCN
  • FM은 shallow structure(cross term degree 2)
  • DCN은 degree $\alpha$의 모든 cross term을 생성
    • 3.1에 따라 layer의 크기를 조절
  • FM과 달리 parameter의 수도 input dimension에 선형 비례

3.3 Efficient Projection

• Cost efficient
  • 원래의 직접 계산법은 cubic cost(세제곱)
  • cross layer는 효율적으로 계산을 하여 input dimension d에 선형 비례
  • $x^{\top}_lw_l$에서 집중
    • projection matrix는 block diagonal structure
    • $w \in \mathbb{R}^d$
    • 따라서 input의 dimension O(d)에 비례

4. Experimental Results

• Dataset
  • Criteo Display Ads Data
    • Continuous features: 13
    • Categorical features: 26
  • Train: 6일
  • Validation & Test: 1일
• Implementation Details
  • Continuous features $\rightarrow$ log transform
  • Categorical features $\rightarrow$ embedding $\rightarrow$ concatenation(1026)

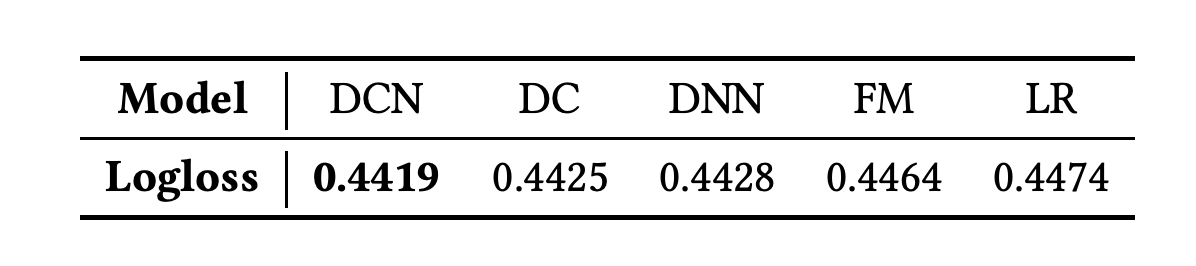
• DCN이 다른 model들을 상회
• DNN에 비해 DCN은 메모리 소비가 40% 적음

• DCN은 다른 모델에 비해 적은 파라미터로 이상적인 logloss를 달성

• 다양한 메모리에서 사용에서 비교해도 DCN이 DNN을 상회

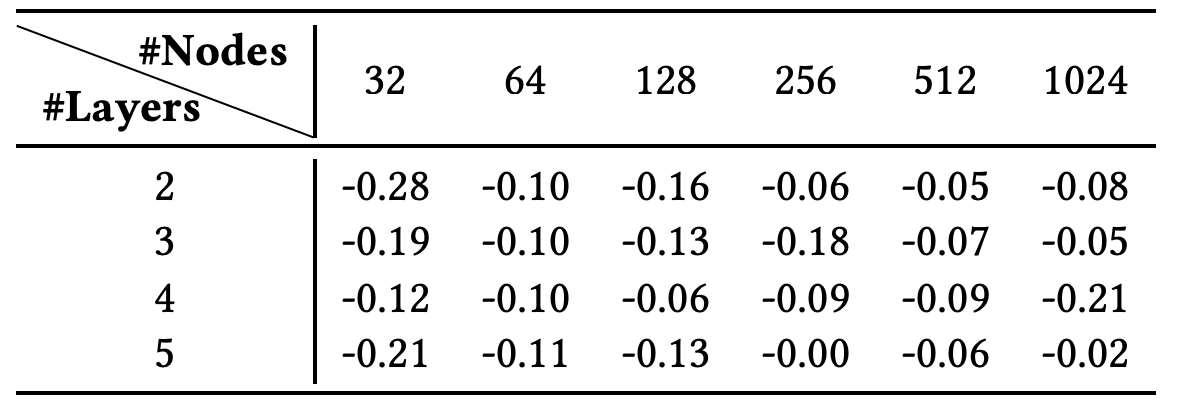
• Node와 Layer 수를 바꿔서 DNN과 DCN 비교
• DCN이 모든 범위에서 DNN을 상회

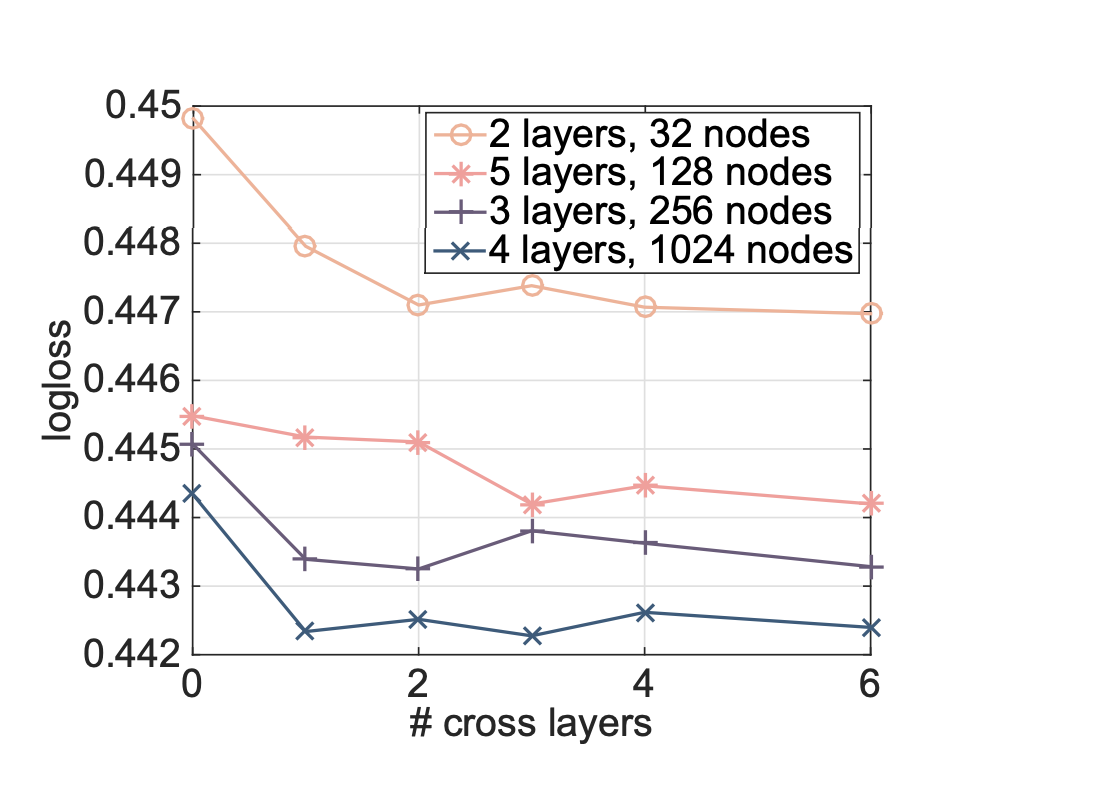
• cross layer의 개수에 따른 성능 변화
• layer가 많아진다고 꼭 성능이 좋아지지는 않음
  • 일정 수준 이후에는 좋아질수도 좋아지지 않을 수도 있음