[Study] Optimizer Functions

1. 7가지 Optimizer Function Notebook
2. Optimizer 함수 numpy 구현
3. 목적
   그 동안 아무 생각 없이 최적화 함수를 사용한 것 같다
   특히 Adam만 default로 사용하고 그 의미를 깊이 고민해본 적 없었다
   이번 기회에 다른 optimizer를 공부하고 구현하며 결과를 비교해보자
   (SGD, Momentum, NAG, Adagrad, RMSProp, Adam, AdamW)

1. 7가지 Optimizers

이름	정의	수식	장점	단점
SGD	미니배치 단위로 기울기를 계산해 단순히 가중치를 갱신	$w := w - \eta \nabla_w L(w)$	1. 단순하고 계산 효율적 2. 작은 데이터셋에서 빠르게 학습 가능	1. 진동 심함 2. 수렴이 느림
Momentum	이전 이동 방향(속도)을 일정 부분 유지해 진동을 줄이고 빠른 수렴 유도	$v_t = \beta v_{t-1} + (1-\beta)\nabla_w L(w)$ $w:= w - \eta v_t$	1. 빠른 수렴 2. 진동 감소	Overshoot(넘침)
NAG	앞으로 이동할 위치를 미리 예측(lookahead)하여 gradient를 계산	$v_t = \beta v_{t-1} + (1-\beta)\nabla_w L(w - \eta\beta v_{t-1})$ $w := w - \eta v_t$	Momentum보다 overshoot 줄임 더 빠르고 안정적 수렴	구현 복잡
Adagrad	파라미터별로 학습률을 조정(gradient 제곱을 누적)	$G_t = G_{t-1} + [\nabla_w L(w)]^2$ $w := w - \frac{\eta}{\sqrt{G_t}+\epsilon}\nabla_w L(w)$	1. 자동 학습률 조정 2. 희소 데이터(sparse)에서 강력	학습률이 점점 빠르게 줄어 수렴 정지 가능
RMSProp	지수이동평균(EMA) 으로 파라미터별 학습률 조정	$s_t = \beta s_{t-1} + (1-\beta) g_t^2$ $w := w - \frac{\eta}{\sqrt{s_t}+\epsilon} g_t$	Adagrad보다 안정적	β에 민감
Adam	Momentum + RMSProp	$m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t$ $v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2$ $\hat{m}_t = \frac{m_t}{1-\beta_1^t}, \hat{v}_t = \frac{v_t}{1-\beta_2^t}$ $w := w - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t}+\epsilon}$	1. 학습 안정적 2. 빠른 수렴 3. 하이퍼파라미터 튜닝 덜 민감	종종 일반화 성능 낮음
AdamW	Adam + Weight Decay(L2 규제)	$w := w - \eta \left( \frac{\hat{m}_t}{\sqrt{\hat{v}_t}+\epsilon} + \lambda w \right)$	일반화 성능 향상 정규화 효과	λ(감쇠 계수) 튜닝 필요

2. 수식 기호 정리

기호	의미
$w$	학습 중인 파라미터
$\eta$	learning rate (학습률)
$m_t$	1차 모멘트(gradient의 지수이동평균)
$v_t$	2차 모멘트(gradient 제곱의 지수이동평균)
$\hat{m}_t, \hat{v}_t$	bias correction된 모멘트
$\beta_1, \beta_2$	각각 1차, 2차 모멘트의 decay rate(보통0.9, 0.999)
$\epsilon$	0으로 나누기 방지용 작은 상수(보통1e-8)

---

3. Logistic Regression 최적화 실험

3-1. 실험 시나리오

• 공통의 예측 함수를 정의
• 임의의 데이터를 생성하여 예측 함수를 학습
• 학습 과정의 최적화 함수를 비교

3-2. 공통 예측 함수

• Logistic Regression
  • binary classification
  • $x \rightarrow p(y=1\mid x)$
  • 출력은 0과 1 사이의 확률
• 모델 구조
  • predict함수로 구현
  • 선형 조합: $z=w^{\top}X + b$
  • 확률 변환: $\hat{y}=\sigma(z)=\frac{1}{1+e^{-z}}$
• 손실함수
  • Binary Cross-Entropy
  • $L = -\frac{1}{m} \sum^m_{i=1}[y_i log(\hat{y}_i) + (1-y_i) log(1-\hat{y}_i) ]$
• 학습
  • 손실 함수를 w, b에 대해 미분해서 gradient 계산
  • optimizer update에 사용
  • weight: $dw = \frac{1}{m} \sum_i(\hat{y}_i - y_i)x_i$
  • bias: $db = \frac{1}{m} \sum_i(\hat{y}_i - y_i)$

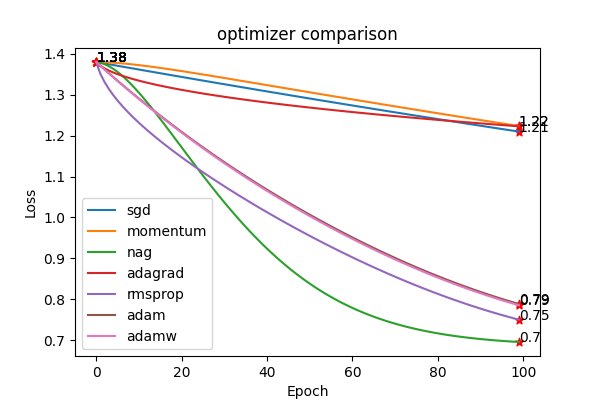
3.3 결과비교

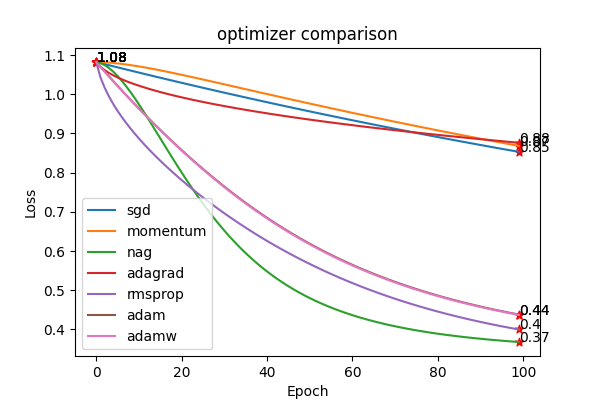
SGD	Momentum	NAG	Adagrad	RMSProp	Adam	AdamW
0.85	0.87	0.37	0.88	0.40	0.44	0.44

from src.optimizers import SGD, Momentum, NAG, Adagrad, RMSProp, Adam, AdamW
from tqdm import tqdm


optimizers = {
    SGD.name: SGD(lr),
    Momentum.name: Momentum(lr),
    NAG.name: NAG(lr),
    Adagrad.name: Adagrad(lr),
    RMSProp.name: RMSProp(lr),
    Adam.name: Adam(lr),
    AdamW.name: AdamW(lr),
}

losses = {}
for name, optimizer in optimizers.items():
    w = _w.copy()
    b = _b.copy()
    loss = []
    
    for epoch in tqdm(range(n_epochs), desc=name):
        y_pred = predict(X, w, b)
        _loss = binary_cross_entropy(y, y_pred)
        dw, db = gradient(X, y, y_pred)

        # update
        w = optimizer.update(w, dw)
        b -= lr * db
    
        loss.append(_loss)

    losses[name] = loss

• optimizer마다 최적화 방법이 다르다
• 최신 optimizer가 최선의 성능을 보장하지 않음
• 실험 단계에서 중요한 hyperparameter로 작용할 수 있음
  • Adam만 사용하지 말고 optimizer를 변경하며 실험
  • 각 optimizer의 hyperparameter를 변경하며 실험