1. 5가지 Loss Function Notebook
2. Loss 함수 numpy 구현
3. 목적
   그 동안 아무 생각 없이 회귀 함수와 분류 함수를 사용한 것 같다
   특히 내부적으로 어떻게 구현되어 있는지 모른채 회귀는 mse, 분류는 cross entropy를 사용하였다
   이번 기회에 어떻게 loss를 구하는지 파악해보자
   (mse, mae, huber, bce, cce)

---

1. 5가지 Losses

1-1. MSE(Mean Squared Error)

• 정의
  • 예측값과 실제값의 차이를 제곱해서 평균낸 값
  • 모델이 얼마나 틀렸는지를 평균 제곱 오차로 나타낸 지표
• 수식
  • $MSE = \frac{1}{m} \sum_i(y_i - \hat{y}_i)^2$
  • $\frac{\partial{L}}{\partial{\hat{y}}} = - \frac{2}{m}(y_i - \hat{y}_i)$
• 장점
  • 오차가 0을 중심으로 매끄럽게 변하므로 gradient descent에 적합
  • 오차가 클 수록 패널티가 크게 부여
• 단점
  • 이상치에 매우 민감 $\rightarrow$ 소수의 이상치가 큰 오차를 유발할 수 있음
  • 단위가 제곱이어여서 해석이 용이하지 않음
• 사용 예시
  • 가격 예측, 수요 예측, 딥러닝 회귀 모델

1-2. MAE(Mean Absolute Error)

• 정의
  • 예측값과 실제값의 차이를 절댓값으로 하여 평균낸 값
  • 모델이 얼마나 틀렸는지를 평균 절대 오차로 나타낸 지표
• 수식
  • $MAE = \frac{1}{m} \sum_i \left\vert y_i - \hat{y}_i \right\vert$
  • $\frac{\partial{L}}{\partial{\hat{y}}} = -\frac{1}{m}\text{sign}(y_i - \hat{y}_i)$
    • $f^{\prime}(x)= \begin{cases} 1 & x > 0 \\ -1 & x \leq0 \end{cases} = \text{sign}(x)$
• 장점
  • 이상치(outlier)에 상대적으로 강건함
    • MSE는 오차의 제곱이기 때문에 상대적으로 적은 penalty
  • 실제 오차 단위와 동일하여 직관적으로 해석 가능
• 단점
  • 절댓값 때문에 gradient가 일정하여 학습 초반 속도가 느릴 수 있음
    • gradient에서 sign 함수는 -1 ~ +1로 오차가 커도 gradient가 커지지 않음
  • gradient가 0이 되는 구간에서 미분 불연속 $\rightarrow$ 일부 optimizer와 학습 불안정 가능
    • momentum, adam, rmsprop 등 gradient의 연속성 가정 $\rightarrow$ 불연속이면 oscillation 발생
    • gradient가 불연속(sign 함수) $\rightarrow$ 미분이 0이 되는 지점에서 값이 튀거나 정의되지 않음
• 사용 예시
  • 집값 예측, 의료 데이터 예측, 이상치가 있는 데이터 회귀

1-3. Huber Loss

• 정의
  • MSE와 MAE의 장점을 결함한 손실 함수(이상치에 덜 민감)
    • 작은 오차일 때 MSE처럼 작동
    • 큰 오차에서는 MAE처럼 작동
  • $\delta$ 라는 하이퍼파라미터를 기준으로 구분
• 수식
  • $L_{\delta}(y, \hat{y}) = \begin{cases} \frac{1}{2}(y-\hat{y})^2 & \text{if} \vert y - \hat{y} \vert \leq \delta \\ \delta(\vert y - \hat{y} \vert - \frac{1}{2} \delta) & \text{if} \vert y - \hat{y} \vert > \delta \end{cases}$
  • $\frac{\partial{L}}{\partial{\hat{y}}} = \begin{cases} -(y-\hat{y}) & \text{if} \vert y-\hat{y} \vert \leq \delta \\ - \delta \cdot \text{sign}(y-\hat{y}) & \text{if} \vert y-\hat{y} \vert > \delta \end{cases}$
• 장점
  • MSE처럼 작은 오차 구간에서는 gradient가 부드러워 학습이 안정적
  • MAE처럼 큰 오차 구간에서는 이상치(outlier)에 덜 민감함
  • $\delta$값을 조정해서 MSE, MAE 중간 정도로 조절 가능
  • 미분이 연속적이어서 gradient 기반 optimizer와 잘 호환됨
• 단점
  • $\delta$ 값을 적절히 설정해야 함
    • 너무 작으면 MAE처럼 느리게 학습
    • 너무 크면 MSE처럼 이상치에 민감
• 사용 예시
  • 이상치가 섞인 회귀 문제(가격 예측, 수요 예측 등)
  • 딥러닝 회귀 모델에서 안정적 학습을 원할 때

1-4. BCE(Binary Cross-Entropy Loss)

• 정의
  • 이진 분류 문제
  • 모델의 예측 확률이 실제 정답 분포와 얼마나 다른지 측정
    • 0 혹은 1
• 수식
  • $L = - \frac{1}{m} \sum_i(y_i \text{log}(\hat{y}_i) - (1-y_i)\text{log}(1-\hat{y}_i))$
  • $\frac{\partial{L}}{\partial{\hat{y}}} = -\frac{y}{\hat{y}}+\frac{1-y}{1-\hat{y}}$
• 장점
  • 확률을 직접 다루므로 출력값 해석이 쉬움(0~1)
  • 예측값이 정답에서 멀수록 손실이 커져 정확한 확률 학습
• 단점
  • Outlier에 민감함 $\rightarrow$ 큰 loss
  • $\text{log}(0) \rightarrow \inf$
    • $\epsilon$을 더하여 해결(1e-7)
• 사용 예시
  • 스팸 메일 분류, 질병 여부 예측, 광고 클릭 여부

1-5. CCE(Categorical Cross-Entropy Loss)

• 정의
  • 다중 분류 문제
  • 모델의 예측 확률이 실제 정답 분포와 얼마나 다른지 측정
    • 여러 개의 클래스
    • 정답 클래스의 확률을 최대화하고 나머지 클래스의 확률은 최소화
• 수식
  • $L = - \frac{1}{m} \sum_i \sum_c y_{(i, c)} \text{log}(\hat{y}_{(i,c)})$
  • $\frac{\partial{L}}{\partial{\hat{y}}} = \frac{y}{\hat{y}}$
• 장점
  • 확률 기반 손실로 출력 해석이 직관적
  • softmax와 함께 사용하면 분류 확률을 자연스레 학습
• 단점
  • 클래스 불균형이 심하면 성능 저하
    • weighted cross entropy 사용 가능
• 사용 예시
  • 이미지 분류, 감정 분류, 제품 카테고리 분류, 텍스트 분류 등

---

2. 선형 회귀 모델

• 분류 모델의 경의 optimizer 실험 참고

2-1. 실험 시나리오

• 공통의 예측 함수를 정의
• 임의의 데이터를 생성하여 예측 함수를 학습
• 학습 시 loss 함수를 비교하여 경과 비교

2-2. 공통 예측 함수

• 선형 회귀 분석
  • Linear Regression
  • $y = x^{\top}X + b$
• Chain Rule
  • $\frac{\partial{L}}{\partial{w}} = \frac{\partial{L}}{\partial{y_{pred}}} \cdot \frac{\partial{y_{pred}}}{\partial{w}}$
  • 따라서 backward $\rightarrow$ 손실함수는 $y_{pred}$에 대한 미분만 계산하면 됨

---

3. 회귀 모형 실험

• Noise를 추가한 회귀 데이터

from sklearn.datasets import make_regression

# regression dataset with noise
X, y = make_regression(n_samples=n_samples, n_features=n_features, noise=1, random_state=42)
y = y.reshape(-1, 1)

• 선형 회귀 모델 학습

from src.optimizers import NAG
from src.losses.regression import MSE, MAE, Huber
from tqdm import tqdm


criterions = {
    MSE.name: MSE(),
    MAE.name: MAE(),
    Huber.name: Huber(),
}

results = {}
for name, criterion in criterions.items():
    # linear regression model
    w = _w.copy()
    b = _b.copy()
    optimizer = NAG(lr) 
    loss = []
    
    for epoch in tqdm(range(n_epochs), desc=name):
        y_pred = predict(X, w, b)
    
        # loss
        _loss = criterion.forward(y, y_pred)
    
        # chain rule
        grad = criterion.backward(y, y_pred)
        dw, db = gradient(X, grad)
    
        # update
        w = optimizer.update(w, dw)
        b -= lr * db

        loss.append(_loss)

    results[name] = {
        "w":w,
        "b":b,
        "loss":loss,
        "criterion":criterion,
    }

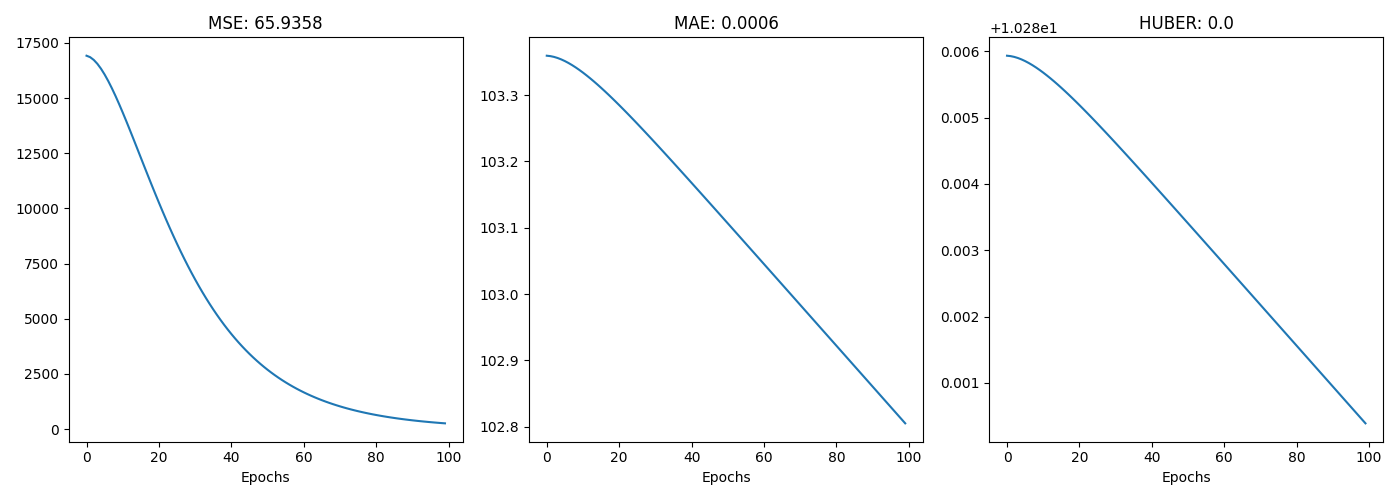
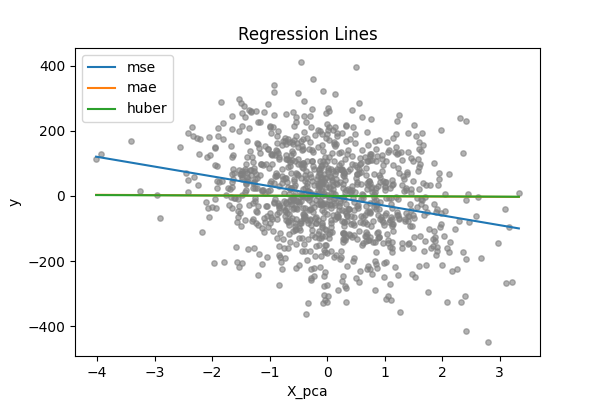
• 의도적으로 noise를 만든 데이터에서 회귀 실험
• MSE와 달리 MAE, Huber loss는 변화가 크지 않는 것을 알 수 있다
  • MSE가 이상치에 예민한 loss임을 확인할 수 있다