Computational graph

• 계산 그래프는 수식의 계산 과정을 노드(Node) 와 엣지(Edge) 로 표현한 것.
• 노드는 연산자 또는 변수 (ex. x, +, *) 를 나타내고, 엣지는 데이터(값)가 흐르는 방향을 나타냄.

예시:

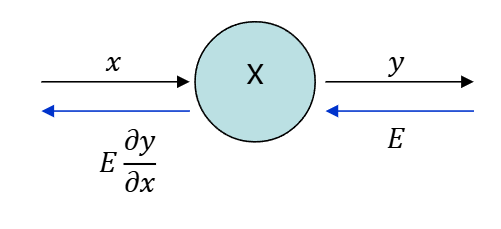
x ----> (*) ----> y  
         ↑  
        3  

• x에 3을 곱해서 y를 만든다면, x, 3은 입력, *는 곱셈 노드, y는 출력.
• 이 흐름을 왼쪽에서 오른쪽으로 계산하는 걸 순전파 (forward),
• 결과로부터 각 입력의 변화율을 오른쪽에서 왼쪽으로 전달하는 걸 역전파 (backward) 라고 함.

---

왜 계산 그래프로 문제를 풀어야 하는가?

• 중간 계산 결과를 저장해둠으로써, 나중에 역전파 시 재계산 없이 바로 미분 계산 가능.
• **역전파 알고리즘(backpropagation)**은 계산 그래프 기반이기 때문에, 효율적인 미분 계산이 가능함.
• 나중에 보게 될 MulLayer, AddLayer는 각각 계산 그래프의 노드를 클래스로 구현한 것.

---

Chain rule (연쇄법칙)

$y = f(x)$

• 합성 함수일 경우, 미분을 각 단계로 나눠서 미분 가능
• 예: $y = f(g(x))$
• 이 경우 $\frac{dy}{dx} = \frac{dy}{dg} \cdot \frac{dg}{dx}$
• 이 방식으로 역전파 때 각 노드별로 "국소적 미분"을 구하고, 이를 연쇄적으로 곱함.

---

덧셈/곱셈 계층 구현

덧셈노드

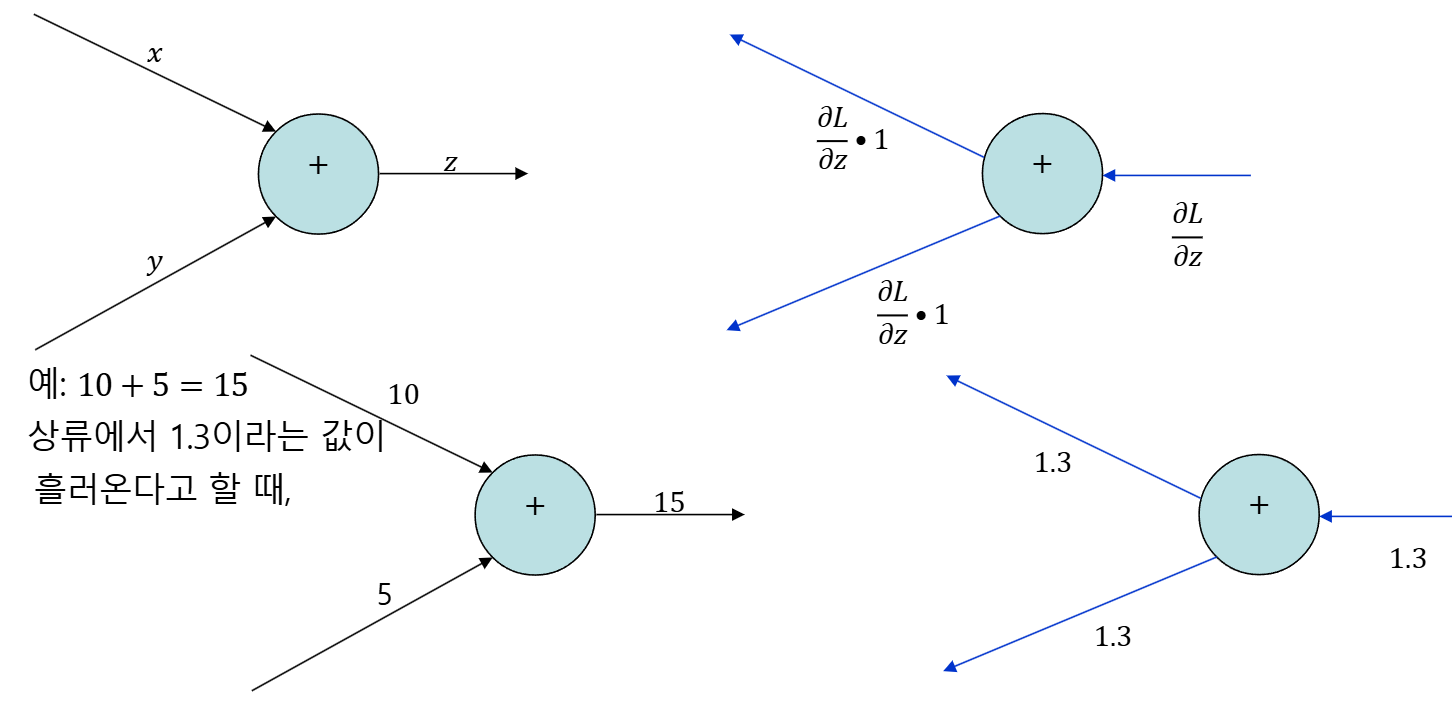
class AddLayer:
	def __init__(self):
		pass  # 덧셈은 중간값 저장 안 해도 되기 때문에 변수 없음
    
	def forward(self, x, y):
		out = x + y
		return out

	def backward(self, dout):
		# 상류로부터 받은 미분(dout)을 그대로 x와 y 양쪽으로 전달
		dx = dout * 1
		dy = dout * 1
		return dx, dy

• forward에서는 단순히 x + y 한 값을 출력
• backward에서는 상류에서 넘어온 기울기(dout)를 그대로 x, y로 나눠줌
  (∂z/∂x = 1, ∂z/∂y = 1)

---

곱셈노드

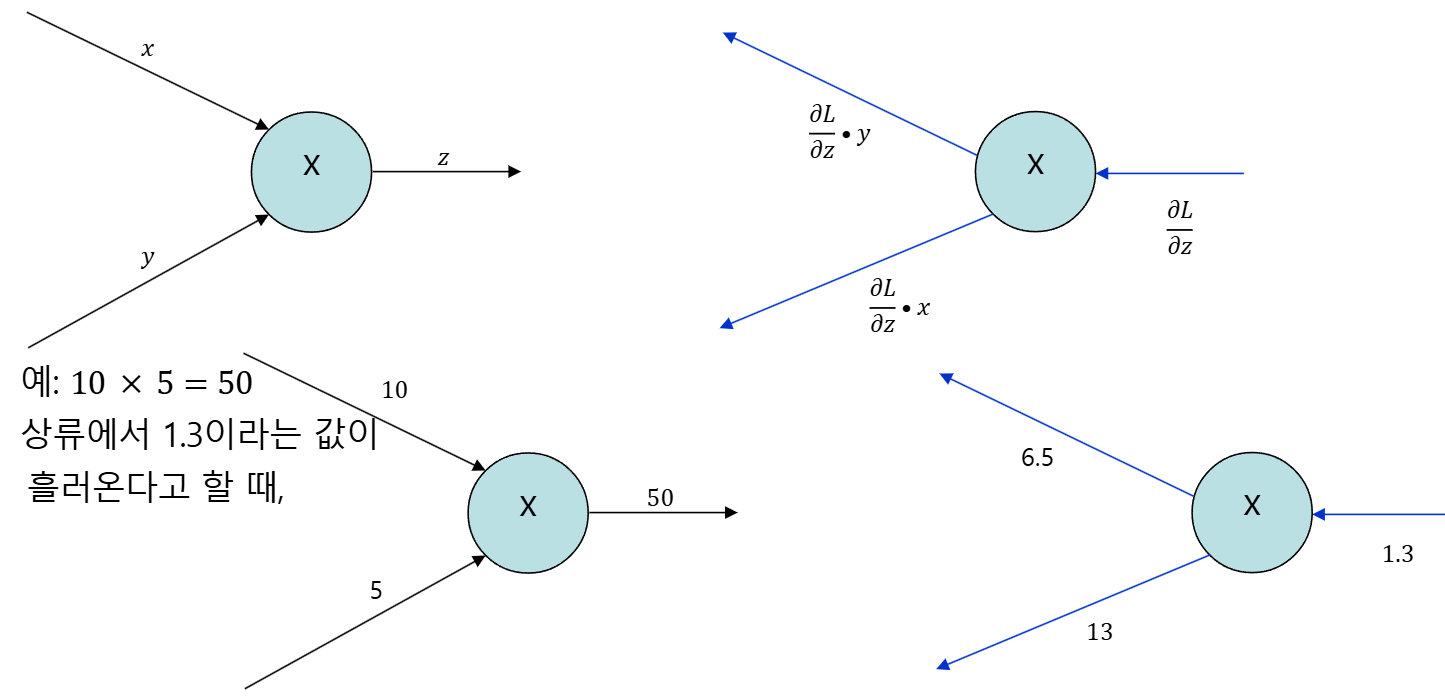
class MulLayer:
	def __init__(self):
		self.x = None
		self.y = None  # 역전파 계산을 위해 x, y를 저장해둠

	def forward(self, x, y):
		self.x = x
		self.y = y
		out = x * y
		return out

	def backward(self, dout):
		# ∂z/∂x = y, ∂z/∂y = x → 상류 미분에 곱해서 전달
		dx = dout * self.y
		dy = dout * self.x
		return dx, dy

• 순전파 시 x * y 계산하고, 두 값은 저장해둠 → 역전파에서 필요
• 역전파에서는 상류 미분(dout)에 y와 x를 각각 곱해서 dx, dy를 구함

---

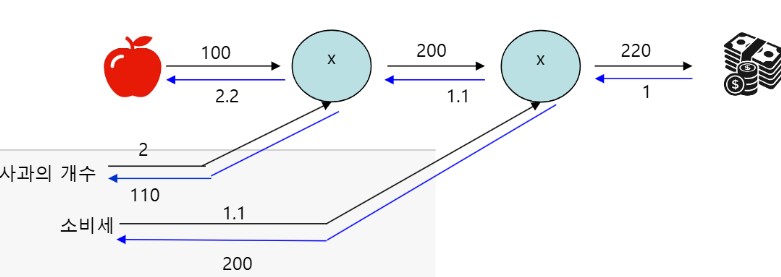
예제 1: 사과 2개 사서 세금 붙은 최종 가격 구하기

price_apple = 100
apple_num = 2
tax = 1.1

계층 구성

mul_apple_layer = MulLayer()  # 사과 개수만큼 곱함
mul_tax_layer = MulLayer()    # 세금 계산

순전파

price_apple_num = mul_apple_layer.forward(price_apple, apple_num)  # 100 * 2 = 200
price_apple_tax = mul_tax_layer.forward(price_apple_num, tax)      # 200 * 1.1 = 220.0

price_apple_num이 먼저 계산되고, 이 값과 tax가 곱해져 price_apple_tax가 됨.
중간 결과값 저장 덕분에 역전파에서 효율적 계산 가능.

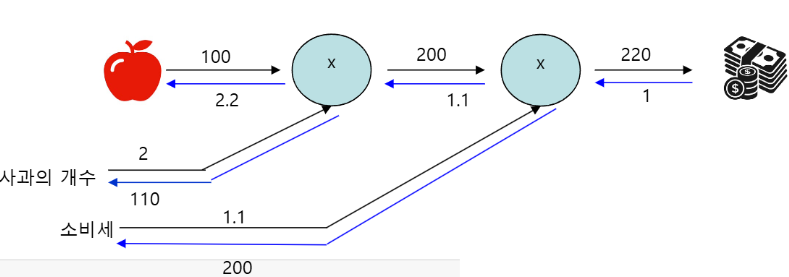
역전파

dprice = 1  # 최종 출력값에 대한 미분 1부터 시작
dprice_apple_num, dtax = mul_tax_layer.backward(dprice)      # tax 방향으로 200, apple_num 방향으로 1.1
dprice_apple, dapple_num = mul_apple_layer.backward(dprice_apple_num)

• dprice = 1은 ∂L/∂L = 1 (출력에 대한 미분은 자기 자신 기준으로 1)
• MulLayer의 역전파는 입력 값을 기억해두었다가, dout에 곱해서 각각의 입력에 대한 미분을 구함.

---

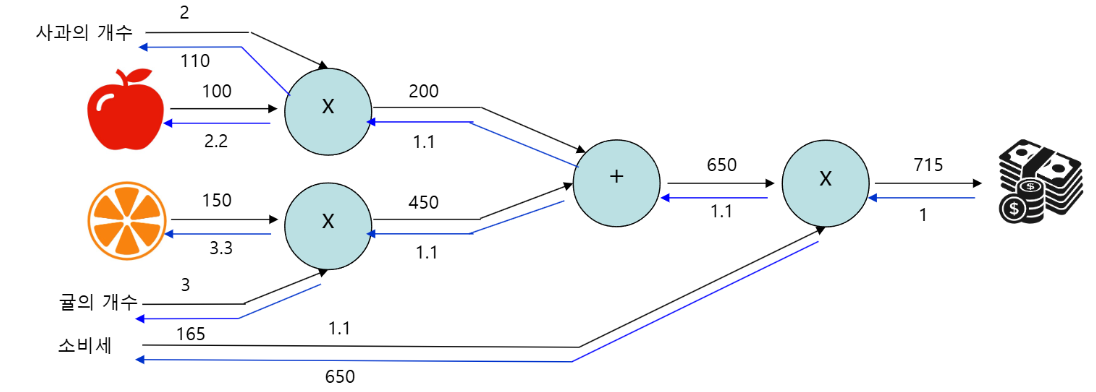
예제 2: 사과 2개, 오렌지 3개, 세금 포함된 전체 가격 계산

price_apple = 100
apple_num = 2
price_orange = 150
orange_num = 3
tax = 1.1

계층 구성

mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

순전파 흐름

price_apple_num = mul_apple_layer.forward(price_apple, apple_num)        # 100 * 2 = 200
price_orange_num = mul_orange_layer.forward(price_orange, orange_num)    # 150 * 3 = 450
price_all_num = add_apple_orange_layer.forward(price_apple_num, price_orange_num)  # 200 + 450 = 650
price_all_tax = mul_tax_layer.forward(price_all_num, tax)                # 650 * 1.1 = 715.0

역전파 흐름

dprice = 1
dprice_all_num, dtax = mul_tax_layer.backward(dprice)   # dprice_all_num=1.1, dtax=650
dprice_apple_num, dprice_orange_num = add_apple_orange_layer.backward(dprice_all_num)  # 1.1씩 나눠짐
dprice_orange, dorange_num = mul_orange_layer.backward(dprice_orange_num)
dprice_apple, dapple_num = mul_apple_layer.backward(dprice_apple_num)

• 역전파 흐름 핵심 포인트: 각 노드가 자신의 입력값과 출력 기울기를 기억하고, 입력 기울기만 계산해서 전달함.
• 각 backward 함수는 자신에게 들어온 미분을 받아, 입력값 저장해둔 거 활용해서 역으로 전달함.

---

정리: 전체 학습 반복 구조

1. 미니배치 선택: 전체 데이터 중 일부만 뽑아 학습 진행
2. 순전파: 입력을 받아 계산 그래프를 따라 출력값까지 계산
3. 오차 계산: 출력과 정답 비교해서 손실 계산
4. 역전파: 손실의 출력에 대한 미분을 시작으로, 각 매개변수의 미분을 구함
5. 매개변수 갱신: 기울기를 기반으로 학습률만큼 매개변수 조정
6. 반복: 이 모든 과정을 여러 epoch 동안 반복