Neural Network

Perceptron의 장단점

• 장점: 복잡한 함수의 표현이 가능하며, 이론적으로 컴퓨터가 수행하는 처리까지 가능
• 단점: 가중치를 설정하는 작업이 수동임

---

퍼셉트론에서 신경망으로

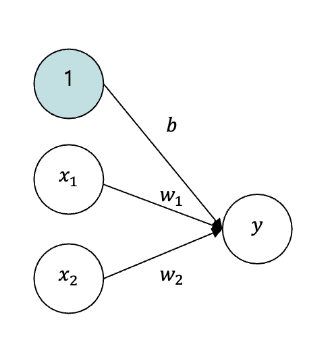
• 가중치가 b이고 input이 1인 뉴런을 추가
• x1, x2, 1 세 개의 input이 뉴런에 입력되고, 입력값에 가중치를 곱한 후 그 합이 0을 넘으면 1, 아니면 0을 출력

---

Activation Function (활성화 함수)

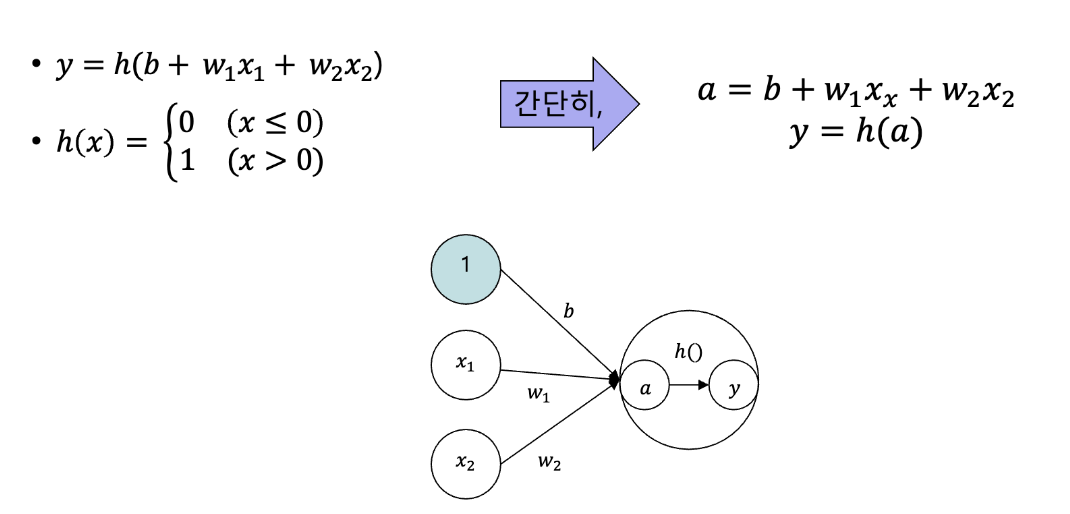
• 입력 신호의 총합을 출력 신호로 변환하는 함수 h(x)

Step Function (계단 함수)

• 입력이 0보다 크면 1, 그렇지 않으면 0

def step_function_basic(x):
    if x > 0:
        return 1
    else:
        return 0

• 넘파이 기반 벡터화 구현 및 그래프:

def step_function(x):
    y = x > 0
    return y.astype(int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)

import matplotlib.pyplot as plt
plt.plot(x, y)
plt.show()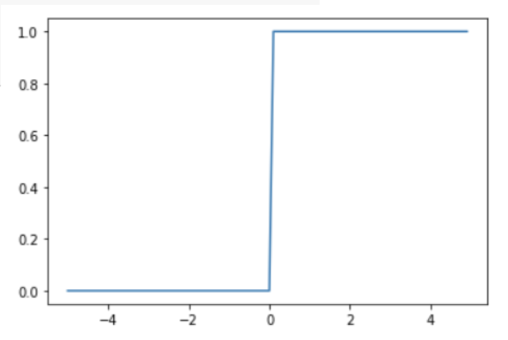

---

Sigmoid Function

• S자 곡선 형태, 연속적이며 미분 가능

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.array([-2, -1.5, -0.5, 0, 0.5, 1.5, 2])
y = sigmoid(x)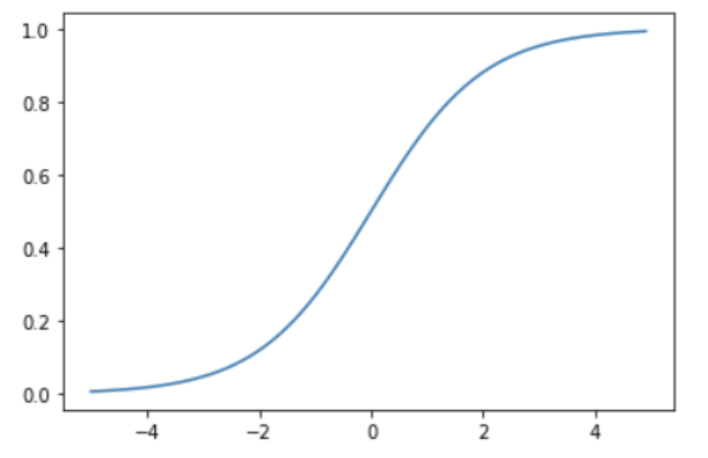

Sigmoid vs Step Function

• 차이점:

  • Sigmoid는 출력이 부드럽게 변화
  • Step은 0 기준으로 급격한 변화

• 공통점:

  • 둘 다 비선형 함수
  • 중요한 입력에는 큰 출력, 그렇지 않으면 작은 출력

---

ReLU Function

• 입력이 0을 넘으면 그대로 출력, 0 이하면 0

def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)

plt.plot(x, y)
plt.show()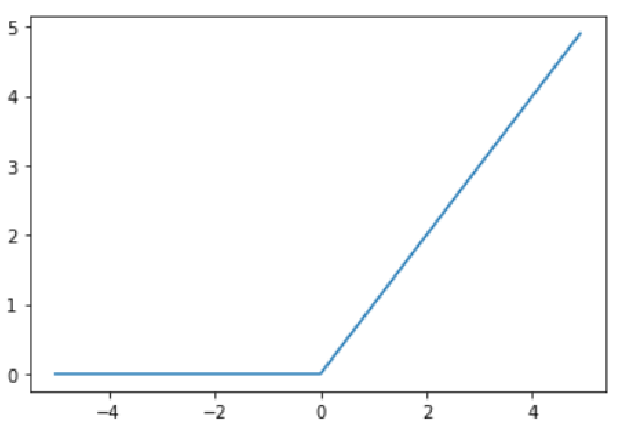

---

Numpy Array 기초

1차원 배열

import numpy as np
arr = np.array([1, 2, 3, 4])
print(arr.ndim)  # 1
print(arr.shape) # (4,)

2차원 배열 (행렬)

n_arr = np.array([[1, 2], [3, 4], [5, 6]])
print(n_arr.ndim)  # 2
print(n_arr.shape) # (3, 2)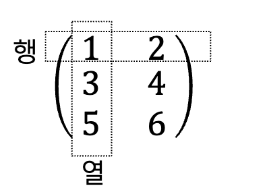

---

행렬의 내적 (Dot Product)

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

result = np.dot(A, B)  # (2,2)

• 내적 조건: A의 열 수 = B의 행 수

---

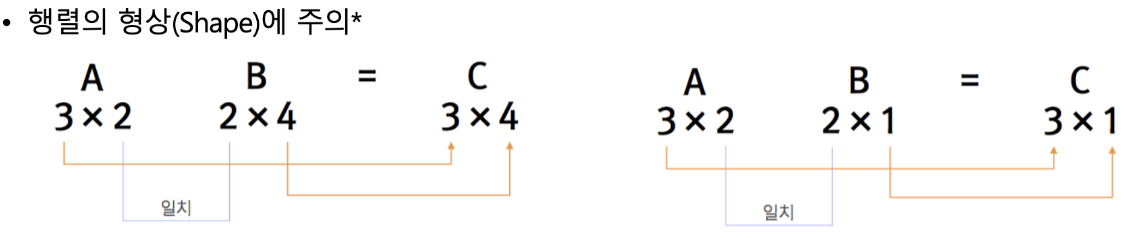
신경망의 내적

---

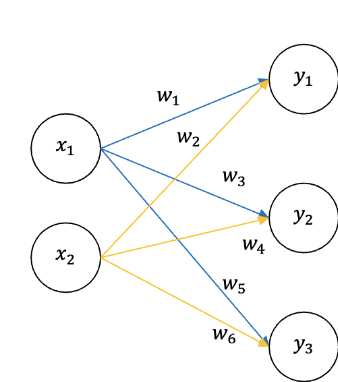
신경망 구현하기 (2개의 은닉층)

초기 설정

import numpy as np

X = np.array([1.0, 0.5])  # (2,)
w1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])  # (2,3)
B1 = np.array([0.1, 0.2, 0.3])  # (3,)

1층

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

a1 = np.dot(X, w1) + B1
z1 = sigmoid(a1)

---

2층

W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])

a2 = np.dot(z1, W2) + B2
z2 = sigmoid(a2)

---

출력층

def identity_function(x):
    return x

W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])

a3 = np.dot(z2, W3) + B3
y = identity_function(a3)

---

전체 신경망 구조 함수화

def init_network():
    network = {
        "weight1": np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]),
        "bias1": np.array([0.1, 0.2, 0.3]),
        "weight2": np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]),
        "bias2": np.array([0.1, 0.2]),
        "weight3": np.array([[0.1, 0.3], [0.2, 0.4]]),
        "bias3": np.array([0.1, 0.2]),
    }
    return network

def forward(network, x):
    W1, W2, W3 = network["weight1"], network["weight2"], network["weight3"]
    B1, B2, B3 = network["bias1"], network["bias2"], network["bias3"]

    a1 = np.dot(x, W1) + B1
    z1 = sigmoid(a1)

    a2 = np.dot(z1, W2) + B2
    z2 = sigmoid(a2)

    a3 = np.dot(z2, W3) + B3
    y = identity_function(a3)
    return y

network = init_network()
X = np.array([1.0, 0.5])
output = forward(network, X)

print(output)

MNIST 손글씨 숫자 인식

MNIST는 손으로 쓴 숫자 이미지(0~9)를 모아 놓은 데이터셋으로, 딥러닝 입문에 자주 사용됩니다.

데이터셋 구성

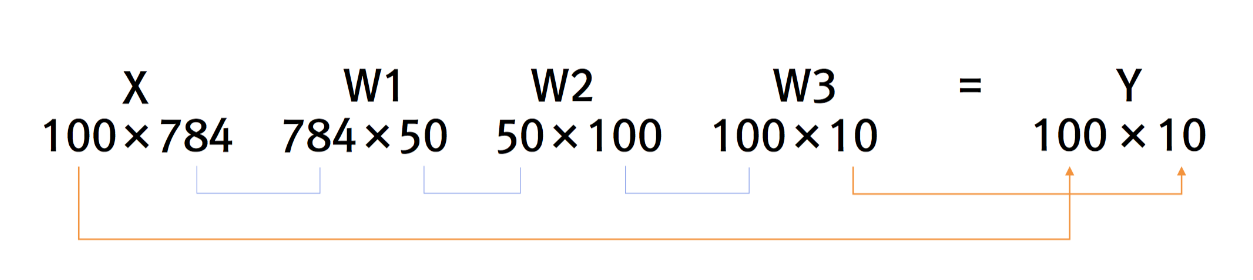
• 28x28 픽셀 흑백 이미지 (784차원 벡터)
• 훈련 데이터: 60,000개
• 테스트 데이터: 10,000개

데이터 로드

import sys, os
import numpy as np
from mnist import load_mnist
from PIL import Image

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

print(x_train.shape)  # (60000, 784)
print(t_train.shape)  # (60000,)
print(x_test.shape)   # (10000, 784)
print(t_test.shape)   # (10000,)

• flatten=True: 이미지를 1차원 배열로 변환
• normalize=False: 정규화하지 않음

이미지 시각화

import matplotlib.pyplot as plt

def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()

img = x_train[0]
label = t_train[0]
print(label)  # 5

img = img.reshape(28, 28)  # 28x28로 reshape
img_show(img)

신경망 추론하기

신경망 구조는 앞서 만든 3층 구조를 그대로 사용합니다.

import pickle

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    def sigmoid(x):
        return 1 / (1 + np.exp(-x))

    def softmax(a):
        c = np.max(a)
        exp_a = np.exp(a - c)
        sum_exp_a = np.sum(exp_a)
        y = exp_a / sum_exp_a
        return y

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)

    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)

    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y

정확도 계산

x, t = get_data()
network = init_network()

accuracy_cnt = 0

for i in range(len(x)):
    y = predict(network, x[i])
    p = np.argmax(y)  # 확률이 가장 높은 인덱스를 예측값으로 사용
    if p == t[i]:
        accuracy_cnt += 1

print("Accuracy:", float(accuracy_cnt) / len(x))  # 예: 0.9352

배치 처리 (한 번에 여러 개 추론)

batch_size = 100  # 배치 크기
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:", float(accuracy_cnt) / len(x))  # 예: 0.9352

요약

• 퍼셉트론에서 출발해 활성화 함수(Sigmoid, ReLU), 행렬 내적을 이용한 신경망 구성
• 층을 쌓아 은닉층이 있는 다층 신경망 구현
• 출력층에서는 항등함수 또는 소프트맥스 사용
• 실제 손글씨 데이터인 MNIST를 이용한 신경망 예측을 통해 실습
• 정확도는 약 93% 이상