Linear

• 선형 모델은 전체 데이터셋에서의 중심선을 찾는다
• 직선의 형태를 갖기 때문에 선형 모델
  

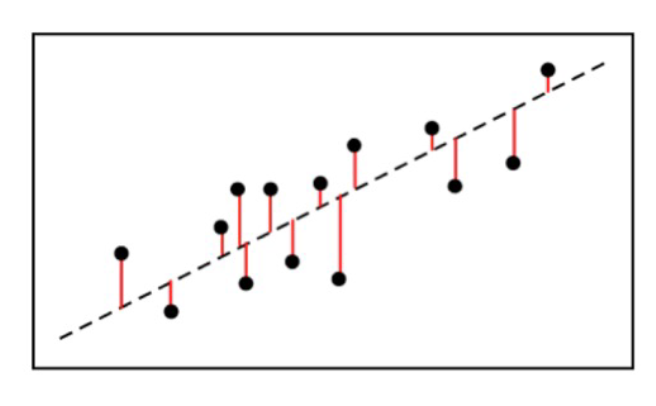
중심선은 잔차(오차)의 제곱의 합이 최소가 되게 하는 선

• 잔차 = 참값 - 예측값
  MSE(mean squared error) 평균제곱오차

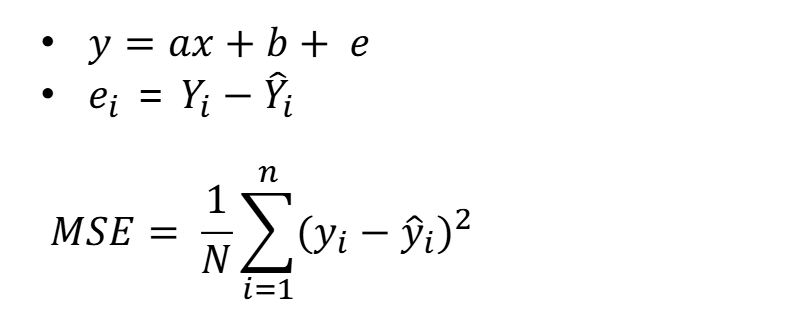
경사하강법

• 어떤 계수가 최소 MSE를 형성하는지는 경사하강법을 통하여 알 수 있다
• 모델의 성능이 좋아질수록 오차가 작아진다
• 오차가 커지면 변곡점 부분의 기울기는 0이 된다

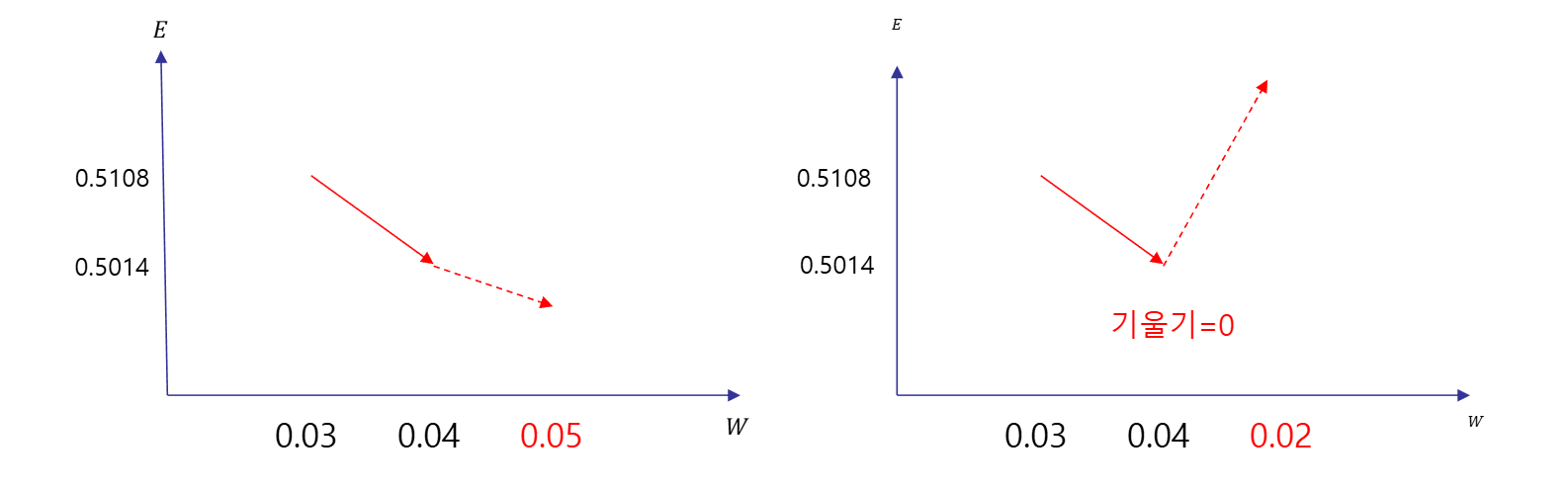
• 기울기가 0이 되는 지점을 찾는 것이 경사하강법의 기본개념
  

특징

• 1차 방정식으로 구성되므로 직선 형태
• 특정 변수가 결과에 미치는 영향을 파악하고자 할때 자주 사용

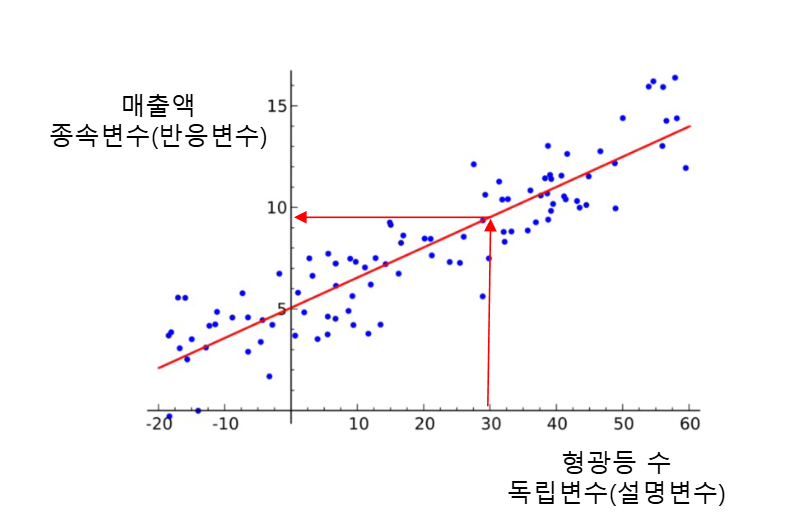
• 독립변수가 하나인 것을 단순 선형회귀 모델, 둘 이상인 것을 다중 선형회귀 모델이라고 한다
  

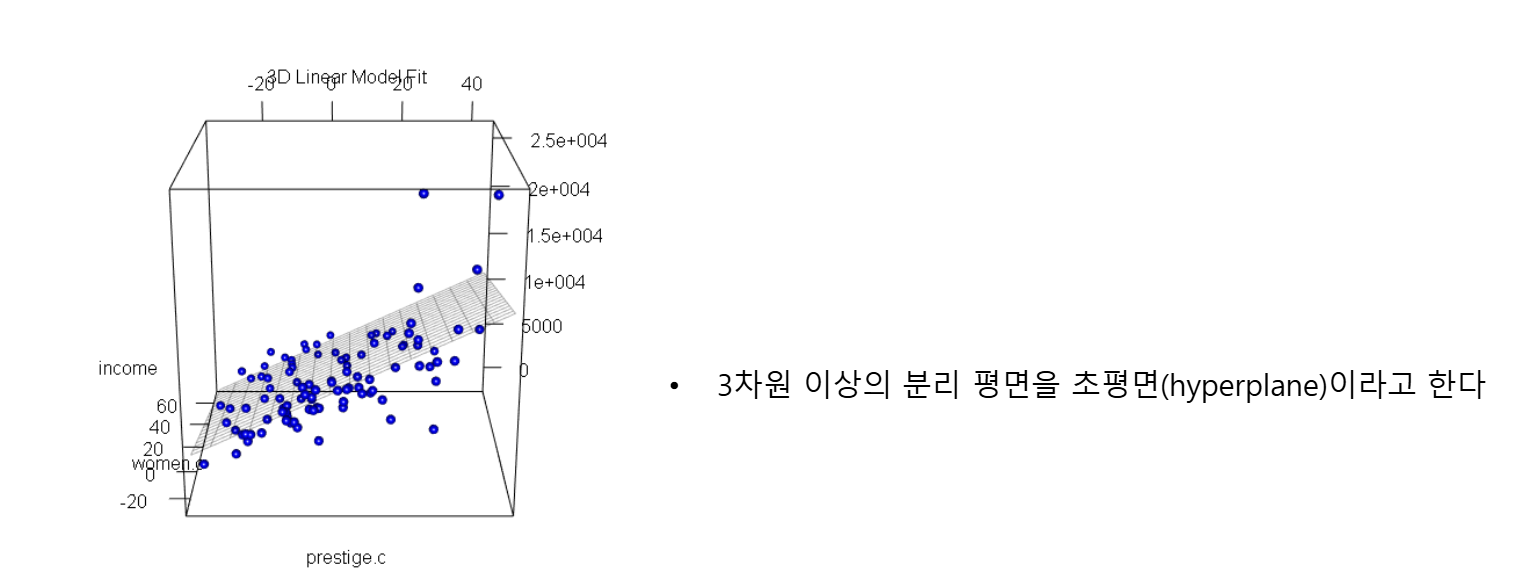
• 1차 방정식이므로 기울기와 절편을 알면 직선을 그릴 수 있다

  • y= ax + b
  • 기울기 = 가중치(weight)
  • 기울기가 클수록 해당 변수의 영향력이 큼

훈련 과정

from sklearn.linear_model import LinearRegression
lr = LinearRegression().fit(X_train, y_train)

새로운 데이터 예측

import numpy as np
print(X_train.shape)

X_new = np.array([[2,9]]) # 다차원 배열로 만든다

result = lr.predict(X_new)

가중치 규제

• 과대적합을 피하기 위하여 모델의 복잡도를 낮출 수 있다

• 가중치(weight)가 작은 값을 갖도록 하는 것 -> 가중치 규제 (Weight Regularization)

• 손실값에 penalty를 추가하여 가중치를 낮춘다

• L1 규제: 가중치의 절댓값에 비례하는 패널티 추가
  

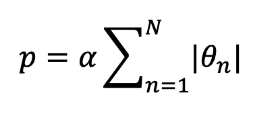
• L2 규제: 가중치의 제곱에 비례하는 패널티 추가
  

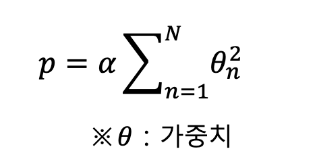
Ridge Regression 리지 회귀

• L2 규제를 사용하는 선형 회귀 모델
• 가중치를 작게 만들어 과대적합을 피한다
• 가중치의 제곱을 사용하므로 아주 작은 가중치는 충분히 제약 효과가 있으므로 가중치가 0이 되는 일은 드물다

from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)

• 훈련 데이터에서 성능은 떨어졌지만, 모델이 일반화되어 테스트 데이터에서는 성능이 올라감
• 모델 단순화를 alpha 매개변수로 조절 가능 (기본값 = 10)
• alpha가 클수록 모델이 단순해진다

from sklearn.linear_model import Ridge
ridge = Ridge(alpha=10).fit(X_train, y_train)

• 선형 회귀와 리지 회귀 모두 훈련 데이터 크기가 클수록 성능이 좋아진다

Lasso Regression 라소 회귀

• L1 규제를 사용
  • L1 규제는 중요 독립변수만 남는 효과를 더 기대할 수 있다
  • 독립변수가 많지만, 일부는 중요 변수인 경우! 좋은 성능을 낼 수 있다
• 비용 계산에 절댓값을 사용하므로 작은 가중치를 가지고 있는 독립변수도 제거하면 효과를 기대할 수 있다

from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)

• alpha 값을 줄여서 모델을 복잡하게 만들면 성능이 좋아진다 (기본값 = 1.0)

from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.1).fit(X_train, y_train)

ElasticNet 엘라스틱넷

• 라지와 라소를 혼합
• l1_ratio 는 L1과 L2의 비율을 조절
  • 0에 가까울수록 L2규제에 가까워지고, 1에 가까울수록 L1에 가까워진다

from sklearn.linear_model import ElasticNet
elasticnet = ElasticNet(alpha=0.2, l1_ratio=0.2).fit(X_train,y_train)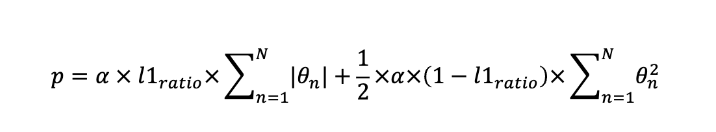

Logistic Regression

• 선형 회귀를 분류 모델로 변환한 것이 로지스틱 회귀이다

장점

• 빠른 학습속도와 빠른 예측속도를 갖는다
• 대용량 데이터셋에서도 잘 작동한다
  • 매우 큰 데이터셋은 물론 값에 0이 많은 희소 데이터에서도 잘 작동
  • 수십만 샘플 이상의 대용량 데이터셋은 계산한 단순화 알고리즘 사용
• 고차원 데이터에서 잘 작동
  • 저차원 데이터에서는 svm등의 성능이 더 낫다

선형 회귀식의 한계

• 선형 회귀식으로 바로 분류 모델을 만들 수는 없다
• 선형 회귀식은 범주형 데이터에 대하여 한계를 갖는다

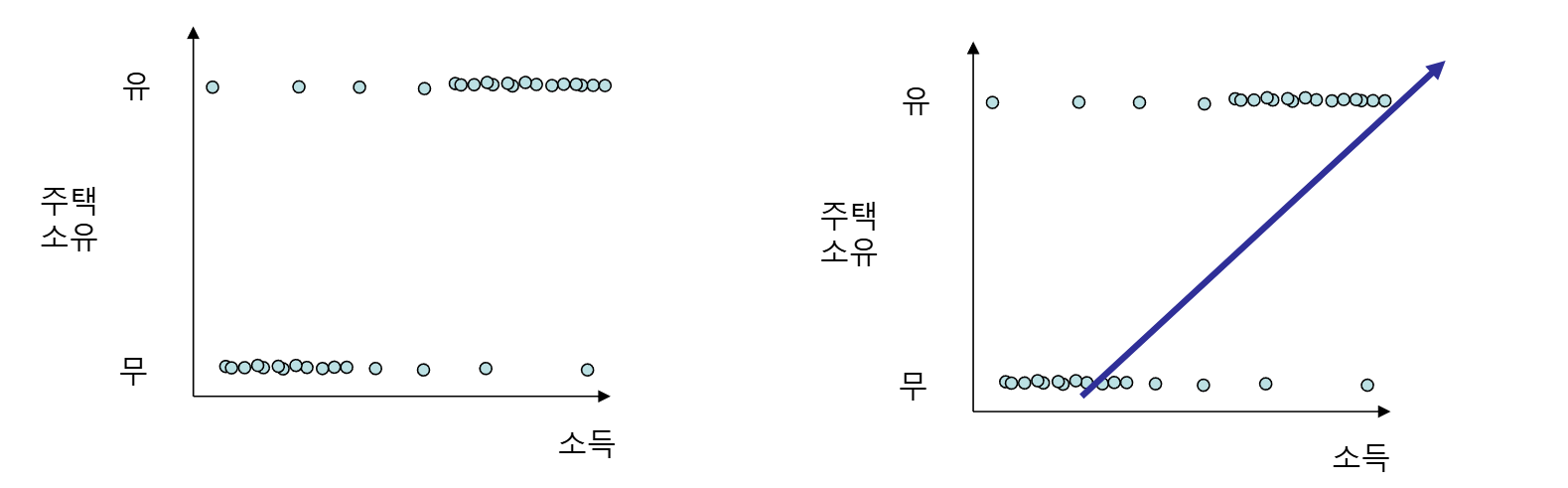
• 매우 많은 데이터를 큰 차이로 예측하지 못하게 된다

확률 변환

• 주택소유를 유/무가 아닌 확률로 보면 경향성 있는 곡선이 그려질 수 있다
  
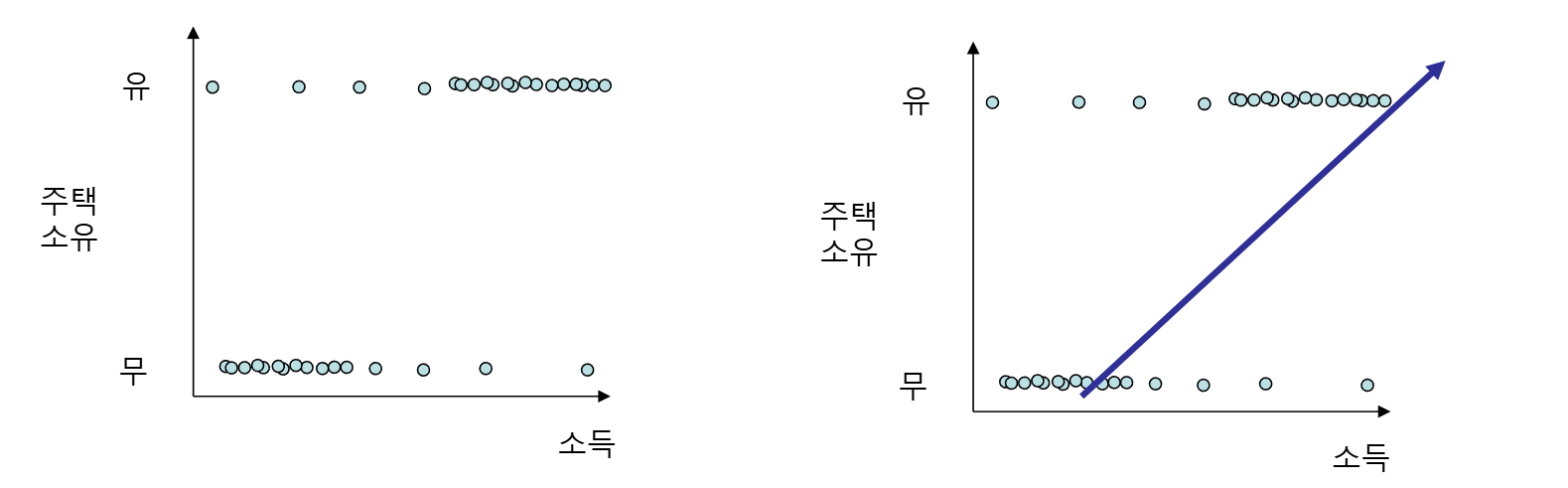
• 이 곡선을 일반 회귀식으로 예측하면 이후 소득이 더 큰 집단이 나타났을때 y축 값이 100% 즉, 1이 넘을 수 있다.

Odds Ratio

• y를 단순 확률이 아닌, 두 확률의 비율로 변환
• y값은 1를 넘을 수 있어 선형 회귀식으로 예측이 가능

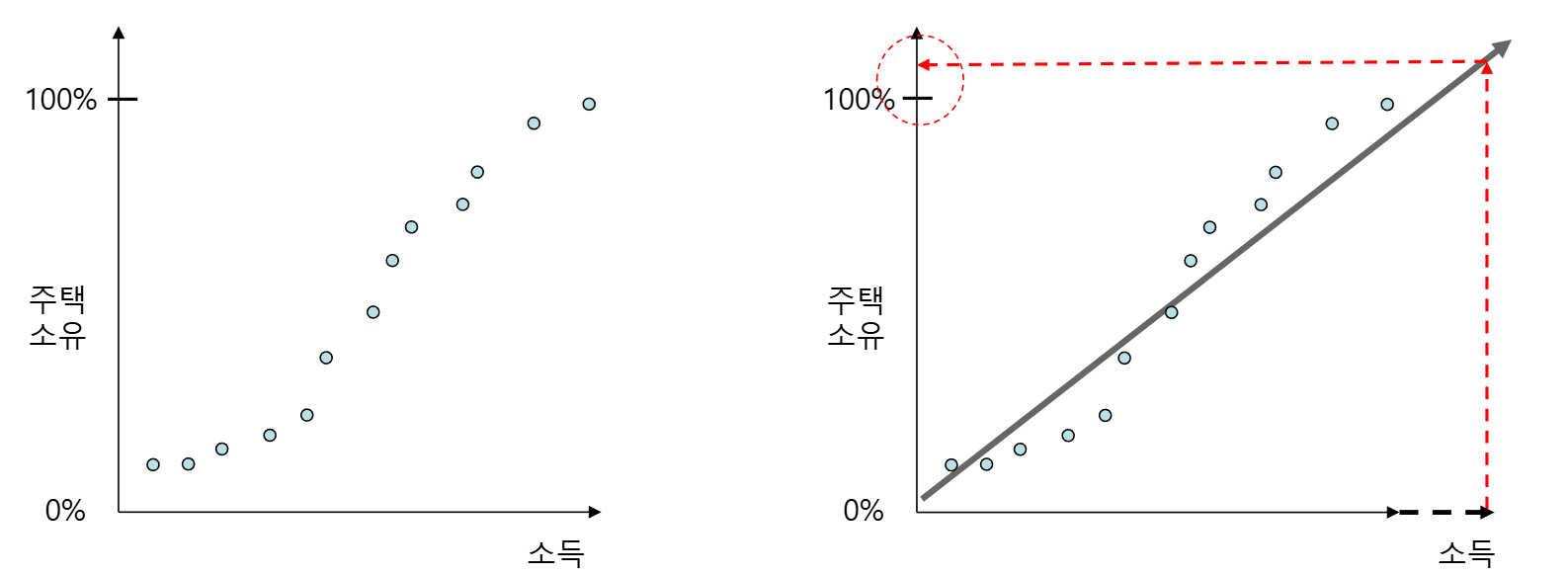
• 즉 독립변수 X에 대하여 종속변수가 1이 될 확률과 0이 될 확률의 비율.

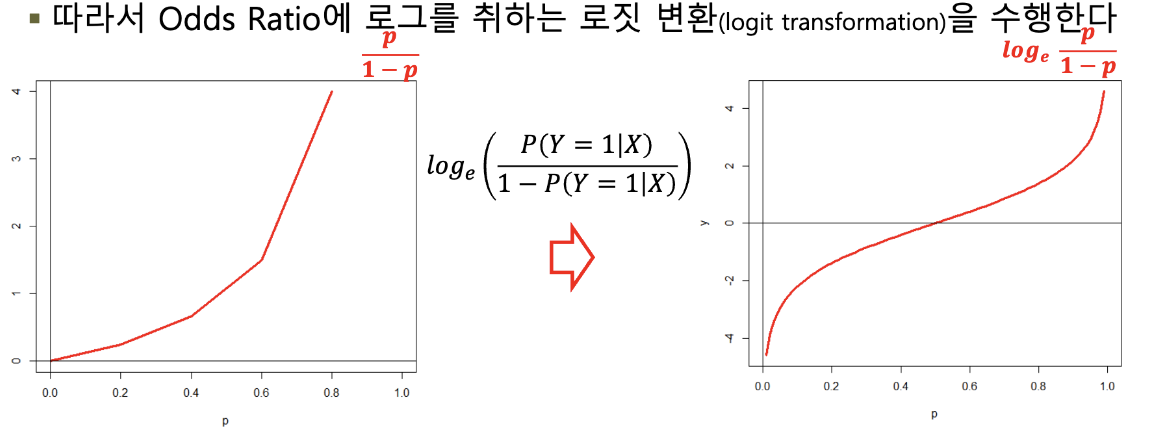
로짓변환

• Odds Ratio 값을 선형 회귀식으로 예측
• 그래프를 최대한 직선식에 맞추기 위해 Odds Ratio에 로그를 취한다
  - 확률 0.5가 넘어서면 곡선이 급격히 상승하여 예측 정확도 떨어짐
  - Odds Ratio는 항상 양수
  

타겟 컬럼 계층화

• 분류 모델이므로 타겟 컬럼화를 계층화 해야함 -> stratify 옵션 사용, 종속변수 지정

X_train, X_test, y_train, y_test= train_test_split(X,y,stratify=y)

• 모델 생성

from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(solver="liblinear")
logreg.fit(X_train, y_train)

규제 낮추기

• 모델의 규제를 낮추기 위하여 매개변수 C값을 높여준다
• C값을 높여주면 모델은 복잡해지고 훈련 데이터에 더 맞추게 된다 (기본값 = 1.0)

logreg = LogisticRegression(C=100, solver="liblinear")
logreg.fit(X_train,y_train)

• C는 cost로서 클수록 비용을 감수하더라도 규제를 완화해 모델을 복잡하게 하겠다는 뜻
  • C가 너무 크면 과적합 너무 작으면 과소적합

최대 훈련 횟수 변경

logreg = LogisticRegression(C=100, solver="liblinear", penalty= "l1", max_iter=150)
logreg.fit(X_train,y_train)

최적화(Optimization)는 모델의 예측값과 실제값 사이의 오차를 줄이기 위해 모델의 매개변수 (가중치, weight)를 조정하는 과정

Naive Bayes

• 통계적 기법을 사용하는 알고리즘
• 훈련 속도가 빠르지만, 일반화 성능은 조금 떨어진다

베이즈 정리

• 베이즈 정리는 조건부 확률을 기초로 한다
• 특정 조건 내에서 어떠한 사건이 발생할 확률
• A사건이 발생했을 때 B사건이 일어날 확률 또는 B사건이 발생했을때 A사건이 일어날 확률

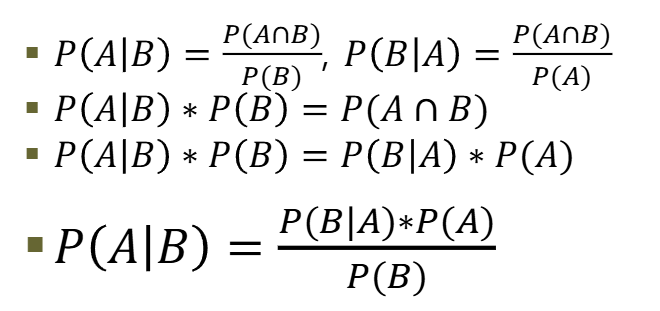
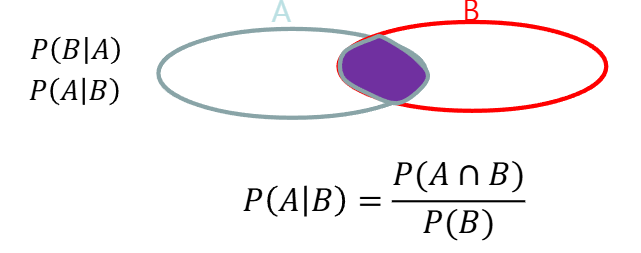
어떤 노트북이 고성능 노트북일때, 그것이 팔릴 가능성

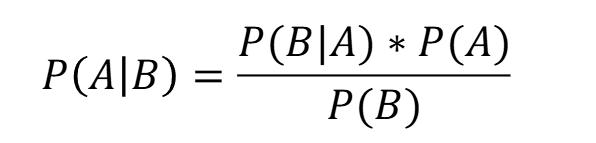
• P(A)는 일반적으로 노트북 판매가 이루어질 확률 (사전확률)
• P(B)는 고성능 노트북일 확률
• P(B|A)는 노트북이 판매될 때 그것이 고성능 노트북일 확률

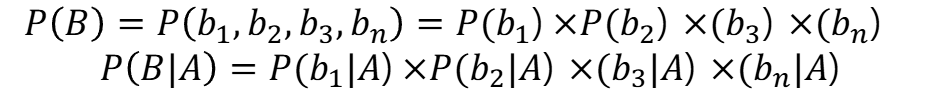
훈련

from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X,y)

GaussianNB & BernoulliNB & MultinomialNB

독립변수가

• 실수형으로 된 경우에는 GaussianNB,
• 0과1의 이진수로 된 경우에는 BernoulliNB,
• 0~K개로 빈도 계산이 된 경우는 MultinomialNB를 사용

BernoulliNB와 MultinomialNB는 텍스트 분류에서 많이 사용되었다

# Bernoulli
from sklearn.naive_bayes import BernoulliNB
bnb = BernoulliNB()
bnb.fit(X,y)

# MultinomialNB
from sklearn.feature_extraction import DictVectorizer
data = [{'house': 100, 'street':50, 'shop': 25, 'car':100, 'tree': 20}, {'house':5,'street':5,'shop':0,'car':10, 'tree':500, 'river': 1}]

dv = DicVectorizer(sparse=False) # 순서에 상관없이 key와 value의 행렬을 구성
X = dv.fit_transform(data)
Y = np.array([1,0])

from sklearn.naive_bayes import MultinomialNB

mnb = MultinomialNB()
mnb.fit(X,Y)

X_test = X_data = [{'house': 80, 'street': 20, 'shop': 15, 'car':70, 'tree': 10, 'river':1}, {'house': 10,'street':5,'shop':1,'car':8, 'tree':300, 'river': 0}]

mnb.predict(dv.fit_transform(X_test))