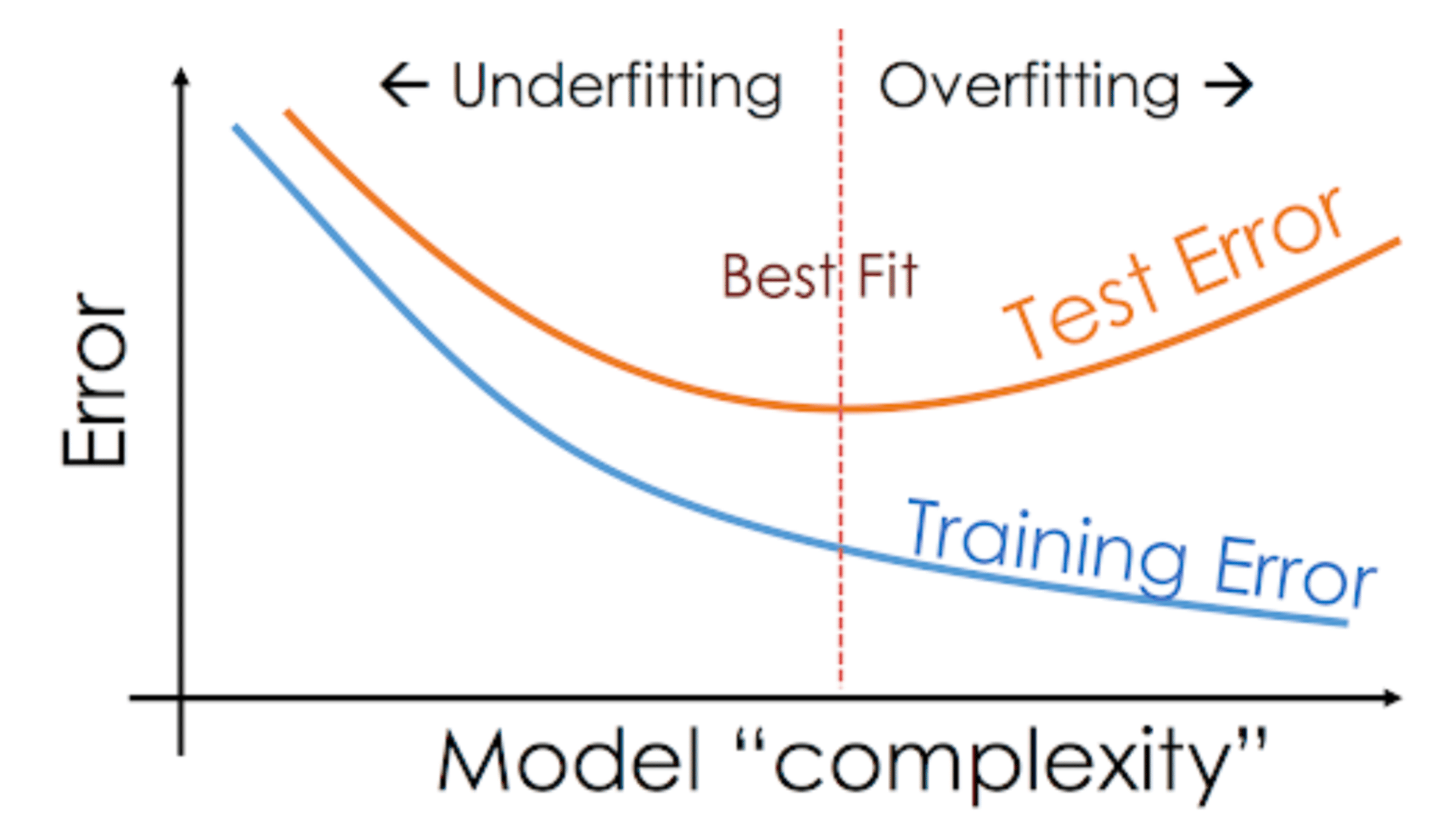
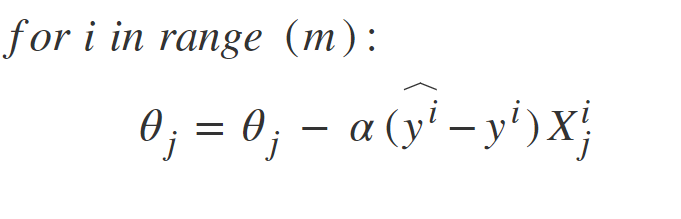- Machine Learning

• 컴퓨터 과학 및 인공지능의 하위 분야로, 프로그램된 명령만 따르는 대신 데이터를 통해 학습할 수 있는 시스템의 구축 및 연구를 다룸
• 샘플(또는 예시 데이터)을 사용하여 성능 기준을 최적화하기 위해 컴퓨터를 프로그래밍하는 것
• 목표: 데이터를 잘 근사하고 유용한 모델을 구축하는 것

- GIGO (Garbage In, Garbage Out)

• 출력의 품질은 입력 데이터의 품질에 직접적으로 의존

- Supervised Learning

• 알고리즘을 훈련하여 결과를 예측하고 패턴을 인식하도록 하는 데에 라벨이 지정된 데이터셋을 사용하는 머신러닝의 한 범주

- Classification

• 이산적인 값을 예측/분류
  ex) 얼굴 인식, 음성 인식, 의학 진단 등

- Regression

• 가격, 급여, 나이 등과 같은 연속적인 값을 예측
  ex) 이미지 생성, 음성 합성

- Unsupervised Learning

• 사람의 감독 없이 데이터를 통해 학습하는 머신러닝의 한 유형

• 지도 학습과 달리, 비지도 머신러닝 모델은 라벨이 없는 데이터를 제공받고 명시적인 지침이나 안내 없이 패턴과 통찰을 스스로 발견

• 클러스터링 (Clustering)
  : 라벨이 없는 원시 데이터를 탐색하고 유사성 또는 차이에 따라 그룹(또는 클러스터)으로 나누는 기법

• 연관 (Association)
  : 대규모 데이터셋에서 데이터 포인트 간의 흥미로운 관계를 밝히는 규칙 기반 접근법

• 차원 축소 (Dimensionality reduction)
  : 데이터셋에서 특징 또는 차원의 수를 줄이는 비지도 학습 기법

- Reinforcement Learning

• AI 기반 시스템(에이전트)이 행동에 대한 피드백을 사용하여 시행착오를 통해 학습할 수 있게 하는 머신러닝의 한 부분

• 탐색 (Exploration)
  : 역동적인 환경에서 잠재적으로 더 우수한 전략을 발견하기 위해 위험을 감수하는 것

• 활용 (Exploitation)
  : 이미 알려진 전략을 통해 즉각적인 보상을 최대화하는 것

---

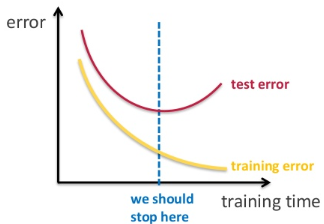
- Dataset의 종류

-> 보통 6:2:2 비율로 나눔

- Training Data

- Validation Data

: Training Set과 별도로 분리된 data set으로, 훈련 중 모델의 성능을 검증하는 데 사용됨

- Test Data

: 학습과 검증이 완료된 모델의 최종 성능을 평가하기 위해 사용됨

-> Validation Set과 Test Set은 모델을 학습시키지 않음!
그렇지만, Validation Set은 학습에 관여함.

-> Training set으로 학습 시에 너무 높은 epoch으로 학습시키면 overfitting될 수 O
-> Validation set을 사용하여 적절한 epoch(위 그림의 파란 선)을 찾음!
-> epoch뿐만 아니라, hyperparameter, hidden layer를 조정할 때에도 사용됨

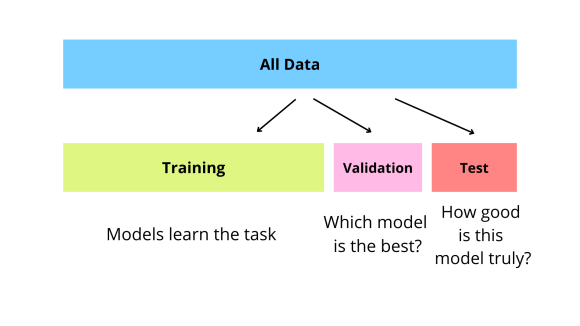
- Overfitting

: Validation Dataset에서의 예측 오류(Prediction error)가 상당히 높거나, Training Dataset에서의 오류보다 높을 때, 모델이 과적합(Overfitting)되었다고 말함

- Machine Learning Process

1. 문제 정의 (Problem Identification)

2. 데이터 수집 (Data Collection)

3. 데이터 전처리 (Data Pre-processing)

4. 모델 선택 및 하이퍼파라미터 설정 (Model selection, Hyper-parameters Configuration)

5. 모델 훈련 -> 하이퍼파라미터 튜닝 (Model Training → Hyper-parameter Tuning)

6. 모델 평가 (Evaluation)

- Data Preprocessing

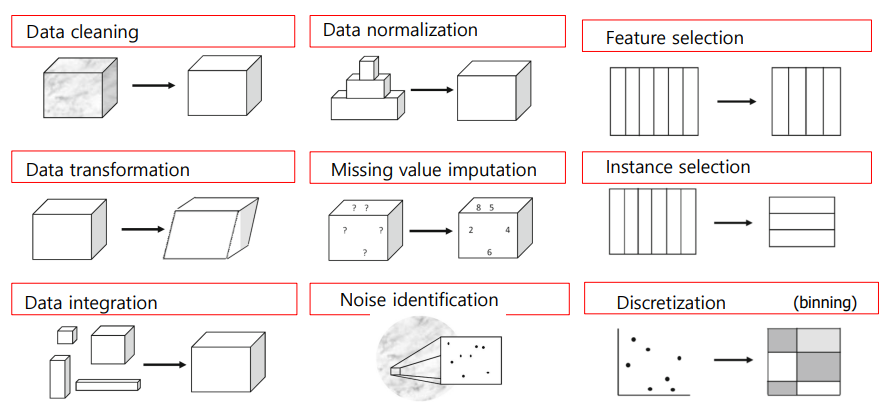
- Data Cleaning

• Missing data
• Invalid data
• Outlier

- Data Transformation

• Discretization
• Normalization
  -> Scale Norm / Z-score Norm / Log-scale Norm
• Reciprocal Transformation
• Data Reduction

---

- Artificial Neural Networks(ANN)

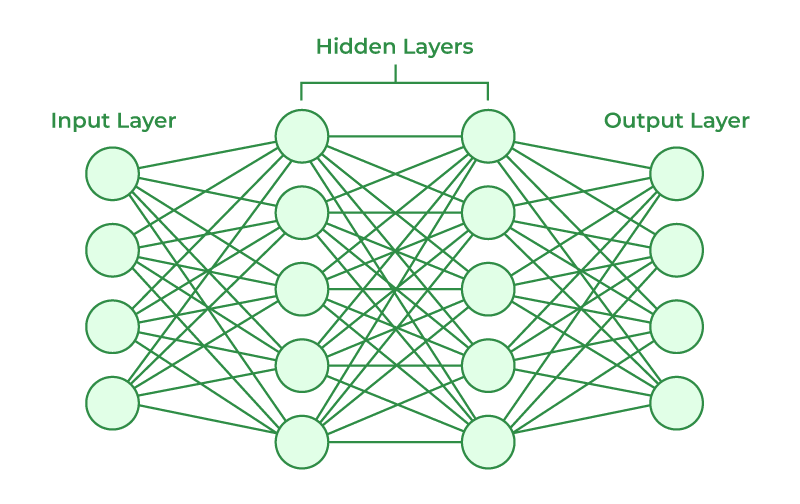
• Input : 벡터 (데이터의 값 -> 벡터의 n_input 차원)
• Output : 벡터 (벡터의 n_output 차원)
  -> ANN의 층(layer)은 가중치(weight), 편향(bias), 활성화 함수(activation function)으로 구성
  

---

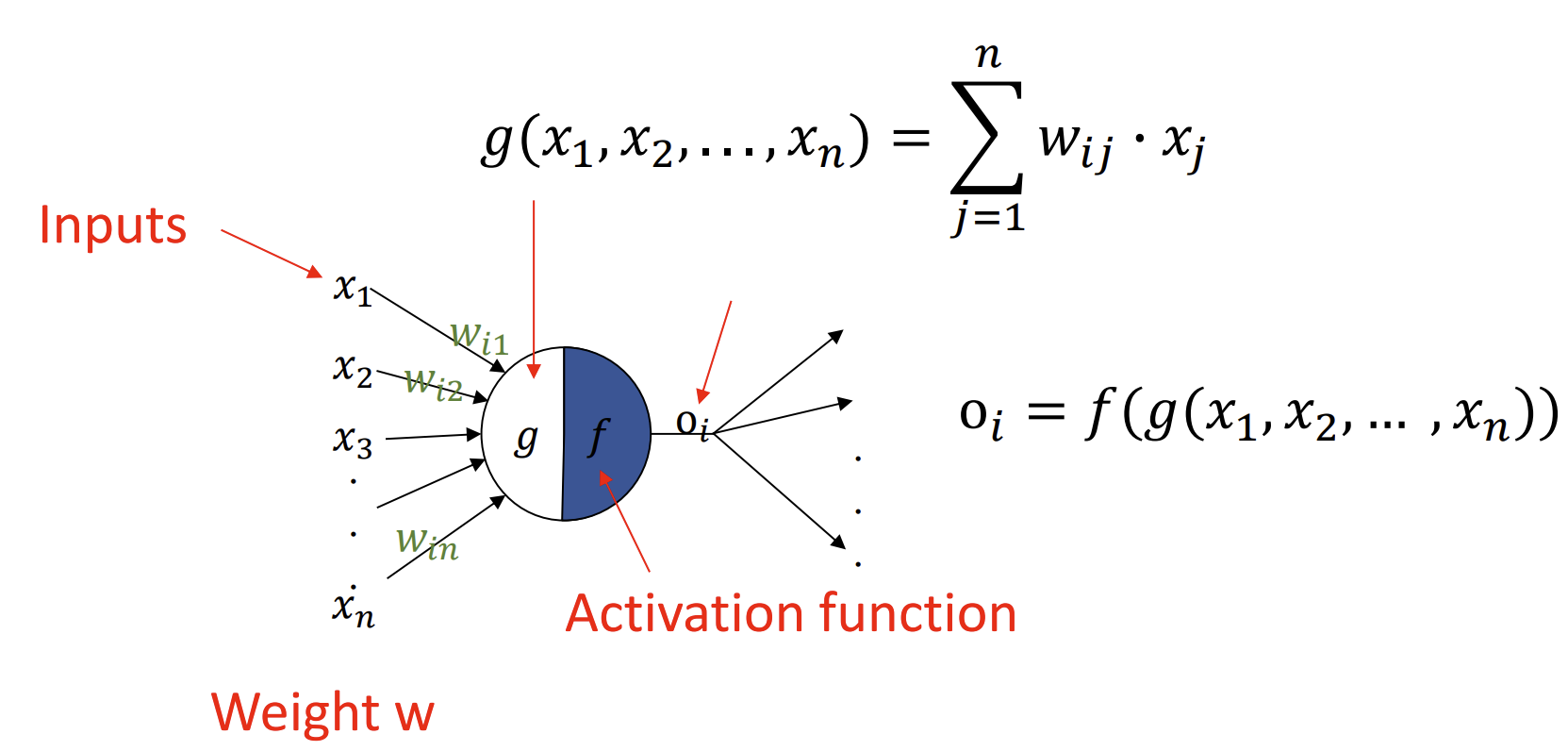
- Perceptron

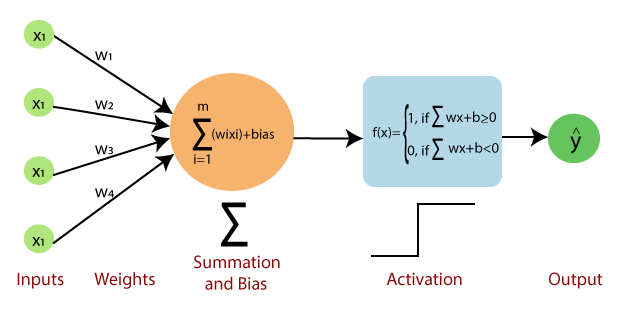
* Perceptron = Perception + neuron
: 인공 신경망의 기본적인 구성 요소이자, 가장 단순한 형태의 신경망 모델
: Input을 가중치와 함께 선형 결합한 후, 이 값에 활성화 함수를 적용해 출력함

-> Single-Layer Perceptron의 경우, 이진 분류 문제를 해결하는 데 사용됨 (선형 분류기 역할, 선형적으로 구분할 수 있는 문제에서만 사용)

• Input : vectors
• Weights(가중치) : 각 Input에 곱해지는 값(학습하면서 조정됨)
• Bias(편향) : 가중치 합에 더해지는 상수 -> 결정 경계의 위치를 조정함!
  * Activation function(활성화 함수) : 입력 값의 선형 결합 결과를 이진 출력으로 변환하는 함수
  -> 가장 기본은 계단 함수(Step function)로, 출력값을 0 or 1로 반환함

<과정>

1. 무작위 가중치를 가진 퍼셉트론과 training set을 준비
2. training set에서 하나의 예제에 대해 입력을 받아 퍼셉트론의 출력을 계산
3. 퍼셉트론의 출력이 예제의 정답 출력과 일치하지 않는 경우:

   <학습 과정>
   -> 출력이 0이어야 하지만 1이 나온 경우, 입력이 1인 가중치를 감소시킴
   -> 출력이 1이어야 하지만 0이 나온 경우, 입력이 1인 가중치를 증가시킴

4. training set의 다음 예제로 이동한 후, 퍼셉트론이 더 이상 오류를 범하지 않을 때까지 2~4단계를 반복

<Logic Gates - AND>

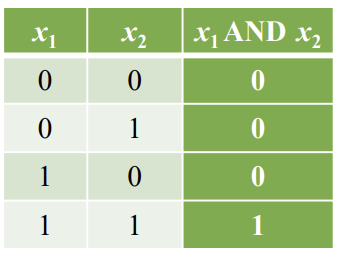
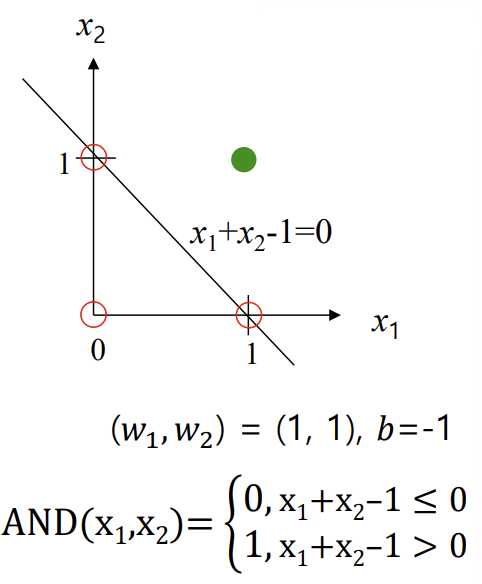
<Logic Gates - OR>

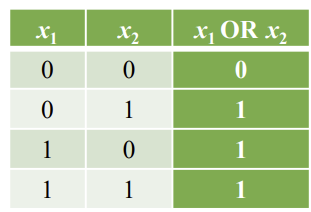
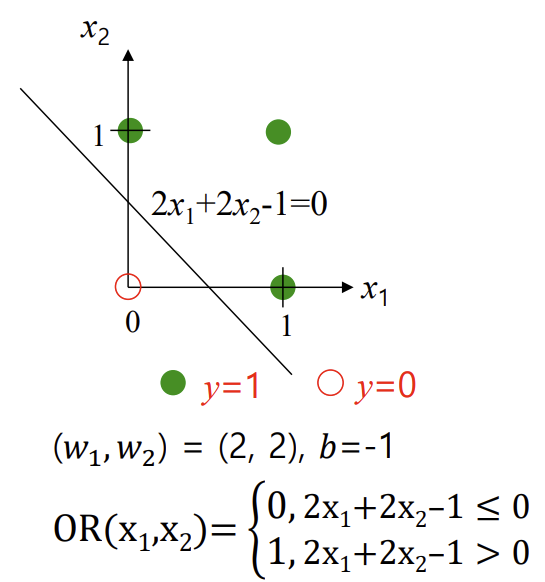
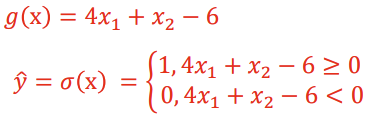
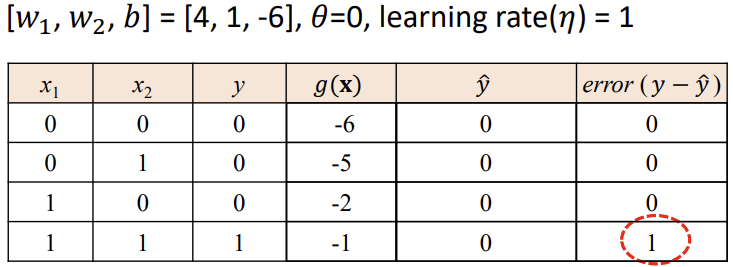
-> 에러 발생 시 weights와 b 업데이트 (g(x) 바뀜)

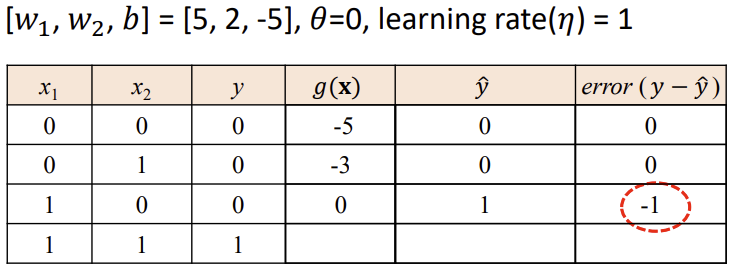
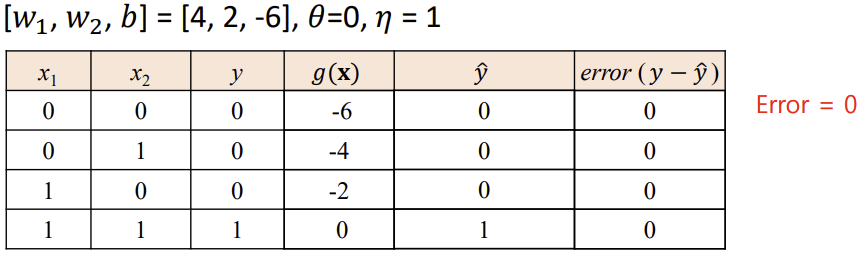
-> 위와 같이 Error = 0이 되면 해당 퍼셉트론은 "Convergence" 라고 표현

- Convergence (수렴)

: 수렴은 학습 과정이 안정된 상태에 도달하여 네트워크의 매개변수(가중치, 편향)가 훈련 데이터에 대해 정확한 예측을 생성하는 값으로 설정된 지점을 의미

---

- Multi-layer Perceptron (MLP)

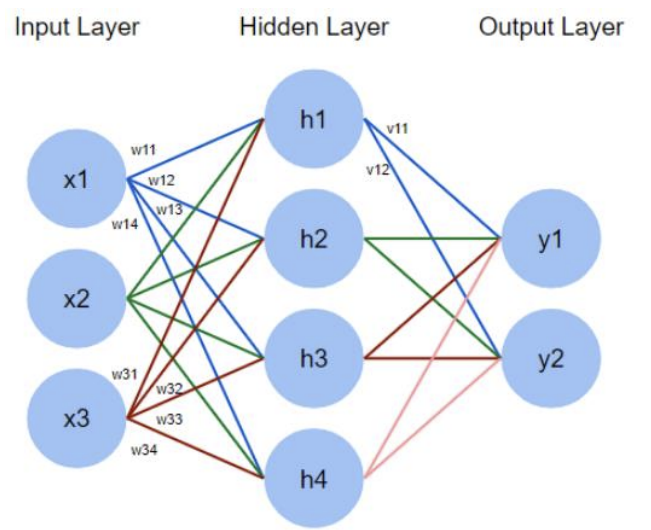
: 다층 퍼셉트론(MLP)은 현대적인 feedforward* 인공 신경망의 명칭으로, 비선형 활성화 함수를 가진 fully connected* 뉴런들로 구성되며, 최소한 3개의 층(Input Layer, Hidden Layer, Output Layer)으로 조직됨

-> 선형적으로 분리할 수 없는 데이터를 구분할 수 있음!

• Feedforward : 데이터가 네트워크의 입력층에서 출력층으로 한 방향으로만 흐르는 구조(단방향 진행)
• Fully connected : 한 층의 모든 뉴런이 다음 층의 모든 뉴런과 연결되어 있음
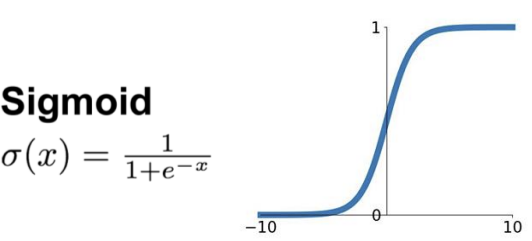
  -> Activation Function : Sigmoid
  
  -> input layer에서 hidden layer로 갈 때의 weight와 hidden layer에서 output layer로 갈 때의 weight는 다름

- Activation functions (활성화 함수)

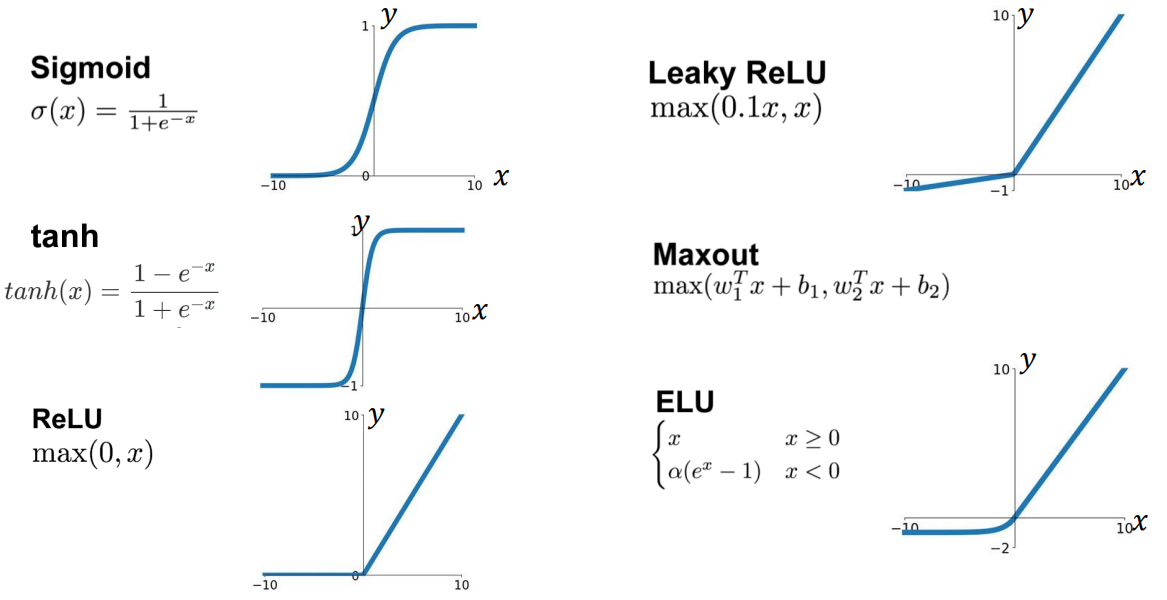
: 인공 신경망의 노드에서 활성화 함수는 각 입력과 그 가중치에 따라 노드의 출력을 계산하는 함수

- Binary Classification with MLP

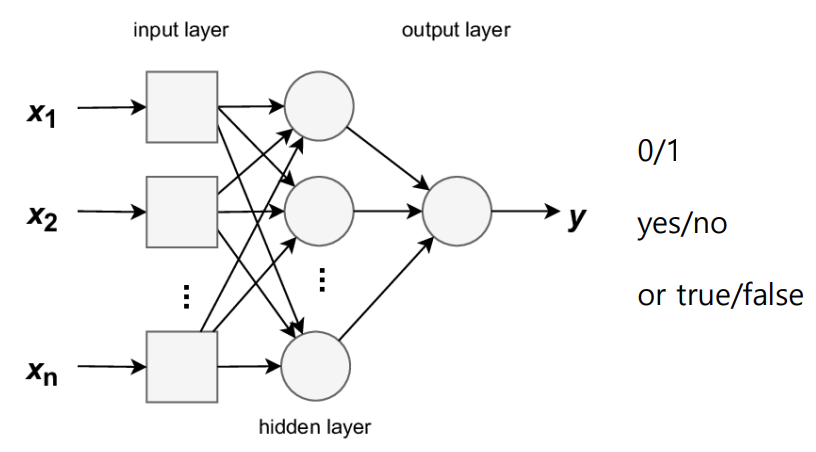
* Logistic Regression

: 특정 결과, 사건 또는 관찰의 확률을 예측하여 이진 분류 작업을 수행하는 지도 학습 알고리즘
: 0/1, 예/아니오, 참/거짓과 같이 2가지의 가능한 결과로 제한된 이진 or 양자 선택의 결과를 제공

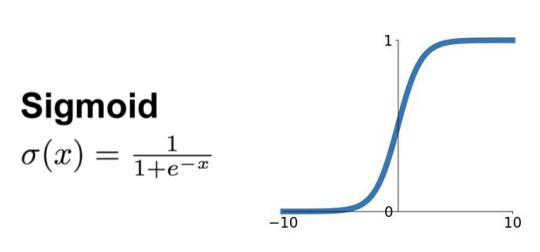
* Sigmoid Activation

: 확률(Probability)을 생성하기 위해 z = w * x + b 를 Sigmoid 함수에 넣음
: 이 함수는 실수 값을 받아 (0,1)범위로 변환함

Sigmoid 함수는 Logistic 함수라고도 불림!

• P(y=1) + P(y=0) = 1 이어야 함
  -> P(y=1) 은 입력값 x가 y=1로 분류될 확률
  -> P(y=0) 은 입력값 x가 y=0으로 분류될 확률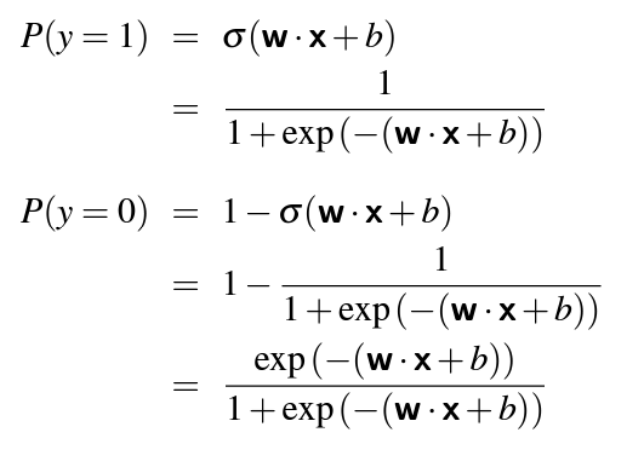

  

-> Sigmoid 함수의 성질:

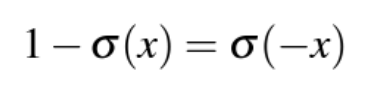
이므로, P(y=0)을 아래와 같이 나타낼 수 O

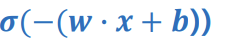
* Logit

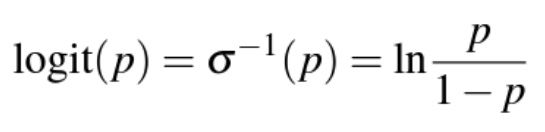
: Logit 함수는 Sigmoid 함수의 역함수
: Odds에 자연로그를 씌운 것

-> Sigmoid함수의 출력값(확률, 0~1사이의 값)을 Logit함수에 넣음으로서 확률을 선형적 공간(-무한대 ~ 무한대)으로 되돌려 가중치와 특성의 기여도를 더 잘 해석하기 위함 (모델의 해석 및 확률의 선형화를 위해)

-> 값이 0보다 큰지 작은지로 판단

* Odds(승산)

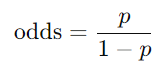
: 확률의 다른 표현법, 실패 비율 대비 성공 비율(성공 확률이 실패 확률에 비해 얼마나 더 큰지를 나타냄)
-> Odds가 크면, 성공확률이 크다는 의미

-> 값이 1보다 큰지 작은지로 판단

* Decision Boundary

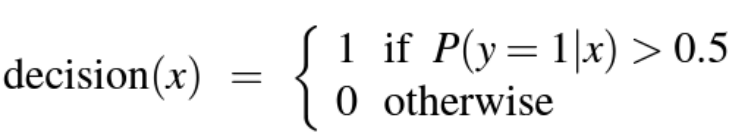
: 두 클래스 간의 경계, 분류 모델이 데이터를 어느 클래스에 속할지 예측할 때 기준이 되는 경계

* Classification with Logistic regression

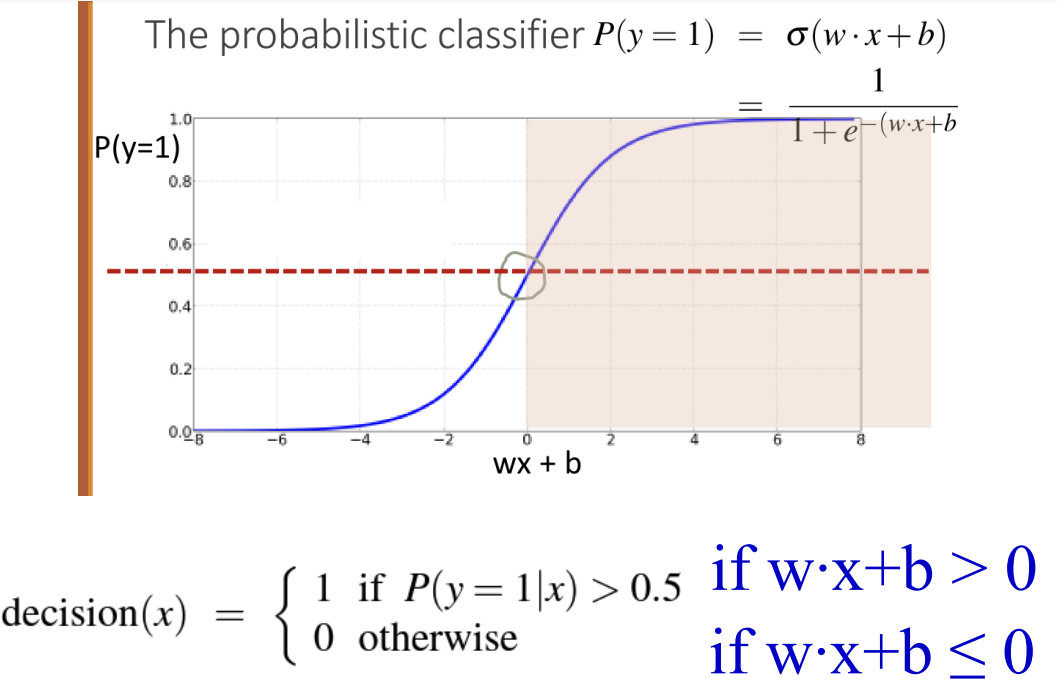
-> 예측된 y^가 실제 y와 최대한 가까워지도록 파라미터(w, b)를 학습하는 것이 목표
-> 손실 함수의 값을 최소화하기 위해 w와 b를 업데이트하는 최적화 알고리즘이 필요함

---

- Optimizing the Neural Networks

• 손실 함수로는 Cross-entropy loss
• 최적화 알고리즘으로는 Stochastic gradient descent 를 사용

* Cross-entrophy loss function (로그 손실 함수)

: 주로 Classification 문제(이진 분류, 다중 클래스 분류)에서 사용되는 손실 함수
: 모델이 예측한 확률 분포와 실제 정답 사이의 차이를 측정하는 용도

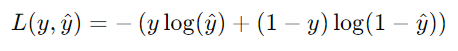
<계산 예시>

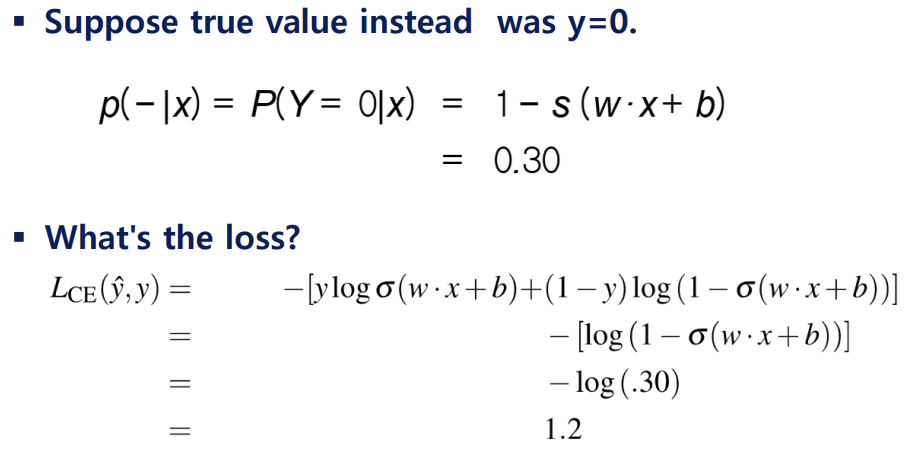
-> 모델이 잘못된 예측을 하면 큰 손실값을 반환함!

*Stochastic Gradient Descent (SGD) 확률적 경사 하강법

: 머신러닝 모델을 학습시키기 위해 사용하는 최적화 알고리즘 중 하나
: 손실 함수 최소화 및 모델의 파라미터(가중치, 편향)를 학습하기 위해 사용됨
: 경사 하강법의 변형된 형태 (손실 함수의 기울기를 계산하여 손실을 최소화하는 방향으로 파라미터를 업데이트 함)
: online algorithm (모든 데이터를 한 번에 처리X, 데이터가 순차적으로 들어올 때마다 실시간으로 처리하는 알고리즘)
-> 각 샘플에 대해 기울기를 계산하고 즉시 모델 파라미터를 업데이트하는 방식이기 때문에 온라인 알고리즘에 해당

<기본 경사 하강법과 차이점>
-> 전체 데이터셋을 사용하지 않고, 하나의 데이터 포인트(샘플) 또는 소규모 미니배치를 사용하여 파라미터를 업데이트함 (고로 더 빠른 업데이트 가능)

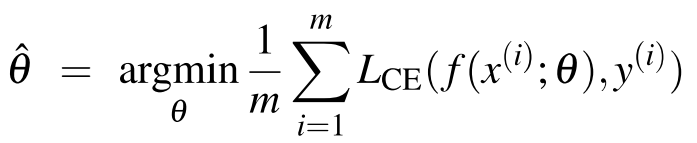
-> theta = (w, b)
-> 예측값 y^ 를 f(x; theta)로 나타냄 (theta에 의존함을 표현)

Logistic Regression에서의 손실 함수는 convex(볼록)

-> 하나의 최소값만 가짐 (최소값 찾는 것이 보장됨)

Neural Networks에서의 손실 함수는 non-convex

-> 지역 최소값(local minima)에 갇혀 global optimum을 찾지 못할 수 O

• Gradients(기울기)
  : 함수 값이 가장 크게 증가하는 방향을 가리키는 벡터
• Gradient Descent
  : 현재 지점에서 손실 함수의 기울기를 찾아 반대 방향으로 이동함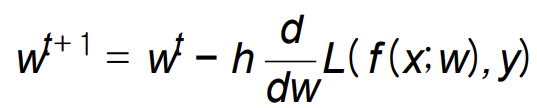
  -> n : learning rate
  learning rate값이 클수록 가중치 w가 더 빠르게 이동함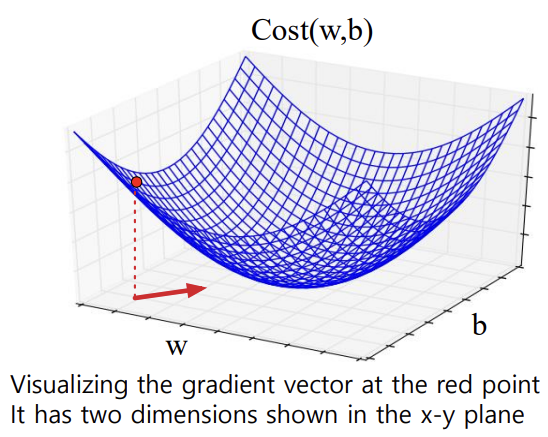

-> 각 차원 wi에 대해, 기울기의 성분 i는 해당 변수에 대한 경사를 나타냄
-> 기울기는 편미분들로 이루어진 벡터로 정의됨

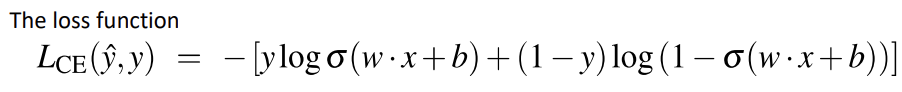
<도함수(derivative)>

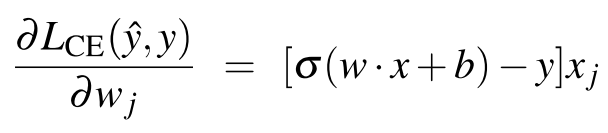
-> 손실 함수 편미분 식을 사용하여 다시 표현하면,