- Multi-class Classification

• 2개보다 더 많은 class를 사용해야 할 땐, multinomial(다항) logistic regression을 사용함
  -> Softmax regression
  -> Multinomial logit

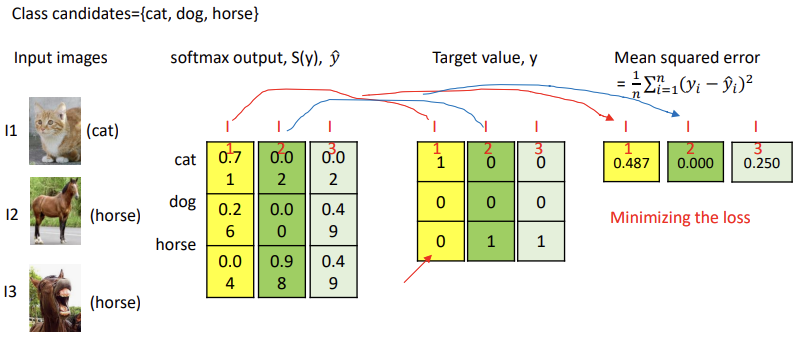
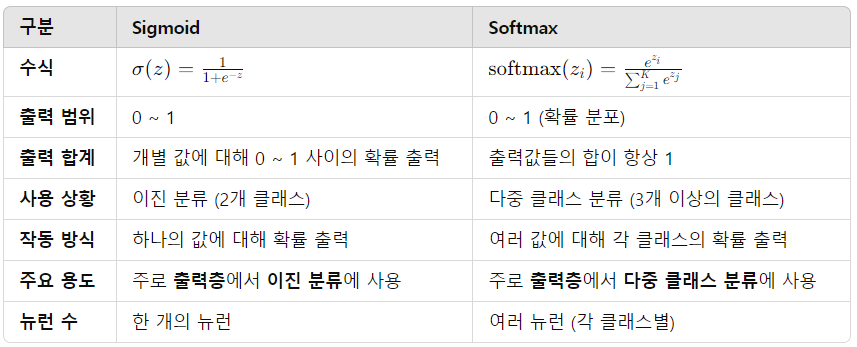
* Softmax function

: 다중 클래스 분류 문제에서 주로 사용됨
: 입력된 값들을 확률 분포로 변환함 (0~1 범위), 모든 값들의 합 = 1
: 입력으로 K개의 실수로 이루어진 벡터 z를 받아, 해당 입력 숫자의 지수에 비례하는 K개의 확률로 이루어진 확률 분포로 정규화함

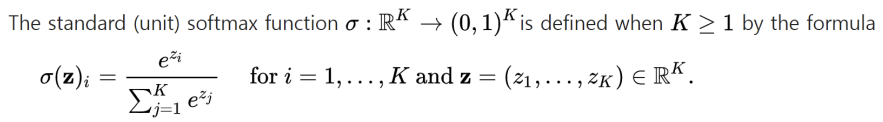
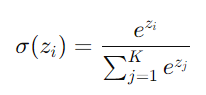
-> 입력값 zi를 각각의 클래스가 선택될 확률로 변환해줌

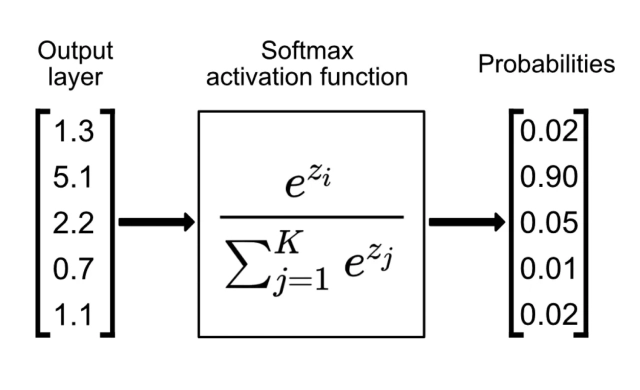
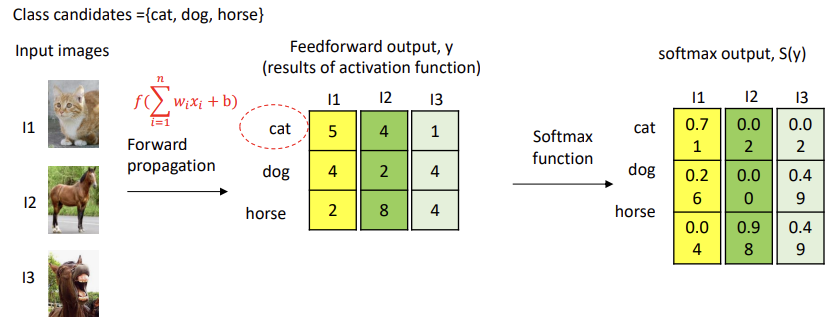
- Regression

: 연속적인 target data 값 추정

• L1 distance = |y-y^|
• MSE : Mean Squared Error
  
  

---

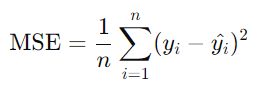
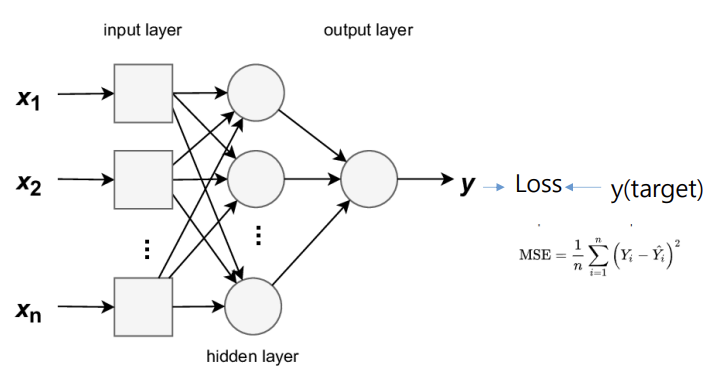
- MLP Learning: Error backpropagation

• Backward error propagation(역전파 오류 수정)은 신경망 학습 과정에서 오류율을 신경망을 통해 다시 전달하여 더욱 정확하게 만드는 과정
  

-> Gradient descent : 오류의 반대 방향으로 가중치를 업데이트함

<V ih의 변화량 구하는 과정>

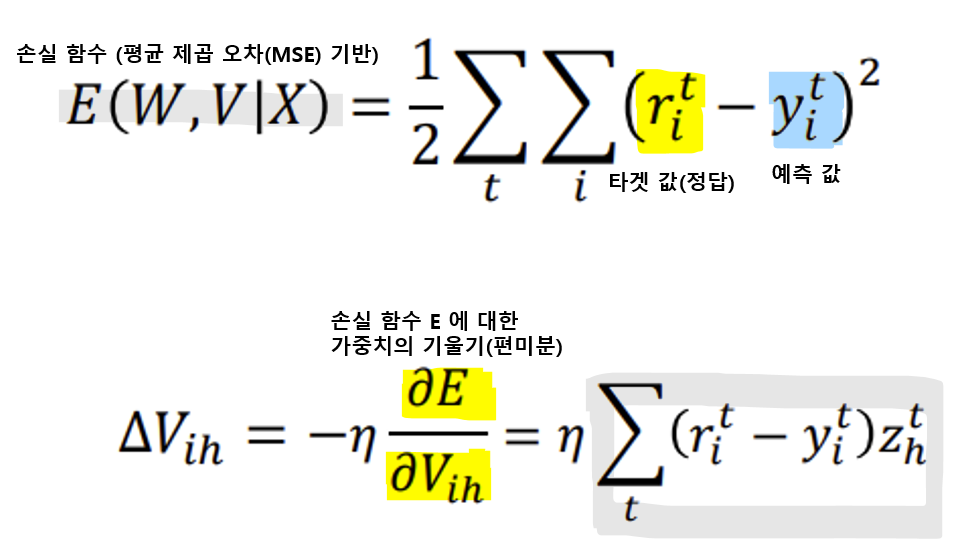
<W hj의 변화량 구하는 과정>

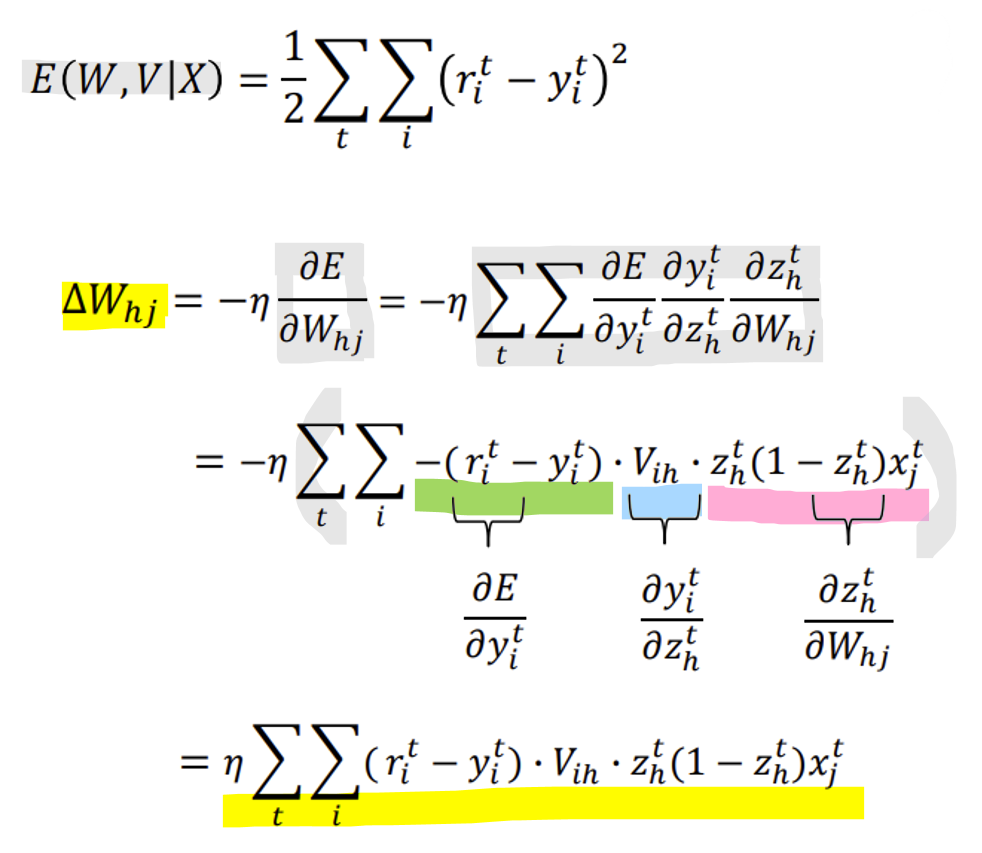
<가중치 업데이트 식>

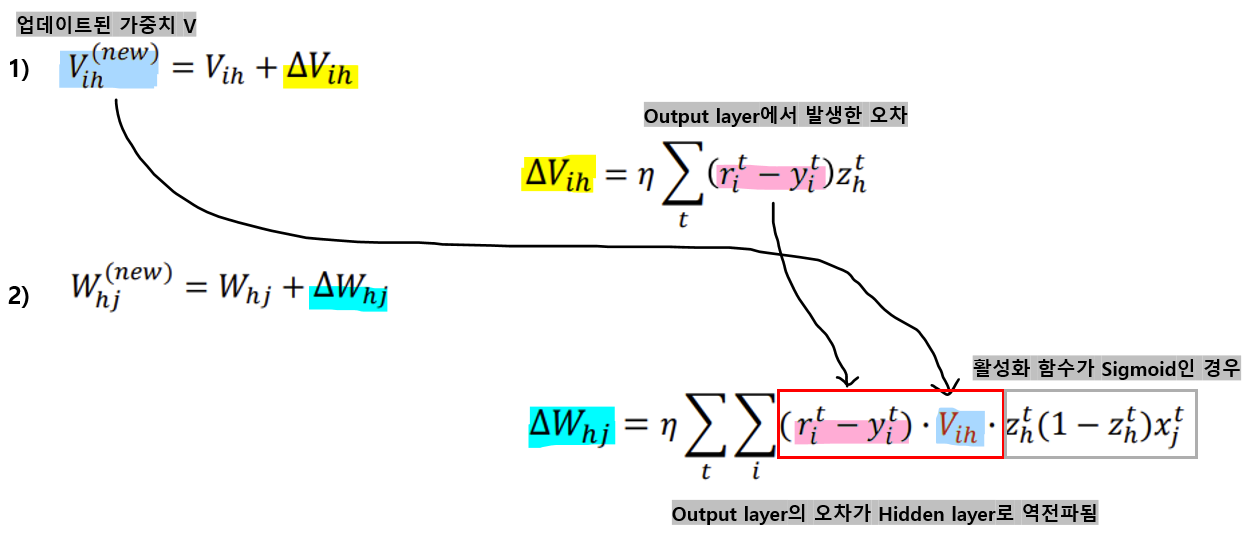
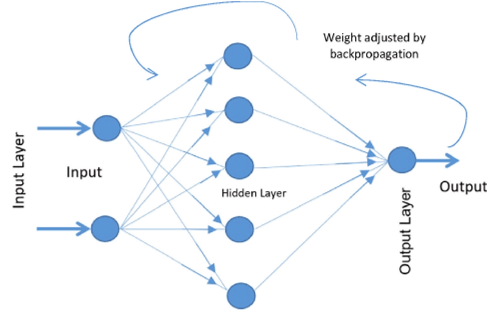
<Error backpropagation(역전파)의 과정>

1. Output layer의 가중치 V ih를 먼저 업데이트
   -> Output layer에서 계산된 오차를 바탕으로, Hidden layer에서 Output layer로 가는 가중치 V를 먼저 수정한다.
2. 업데이트된 V(new)를 사용하여 Hidden layer에서 발생한 오차를 계산하고, 그 오차를 바탕으로 Input layer와 Hidden layer 사이의 가중치 W hj를 업데이트

---

- Error Backpropagation - tanh

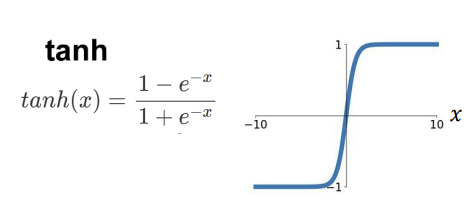
<tanh의 미분 과정>

---

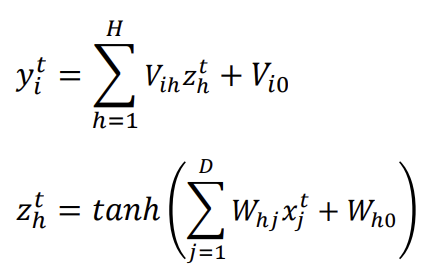
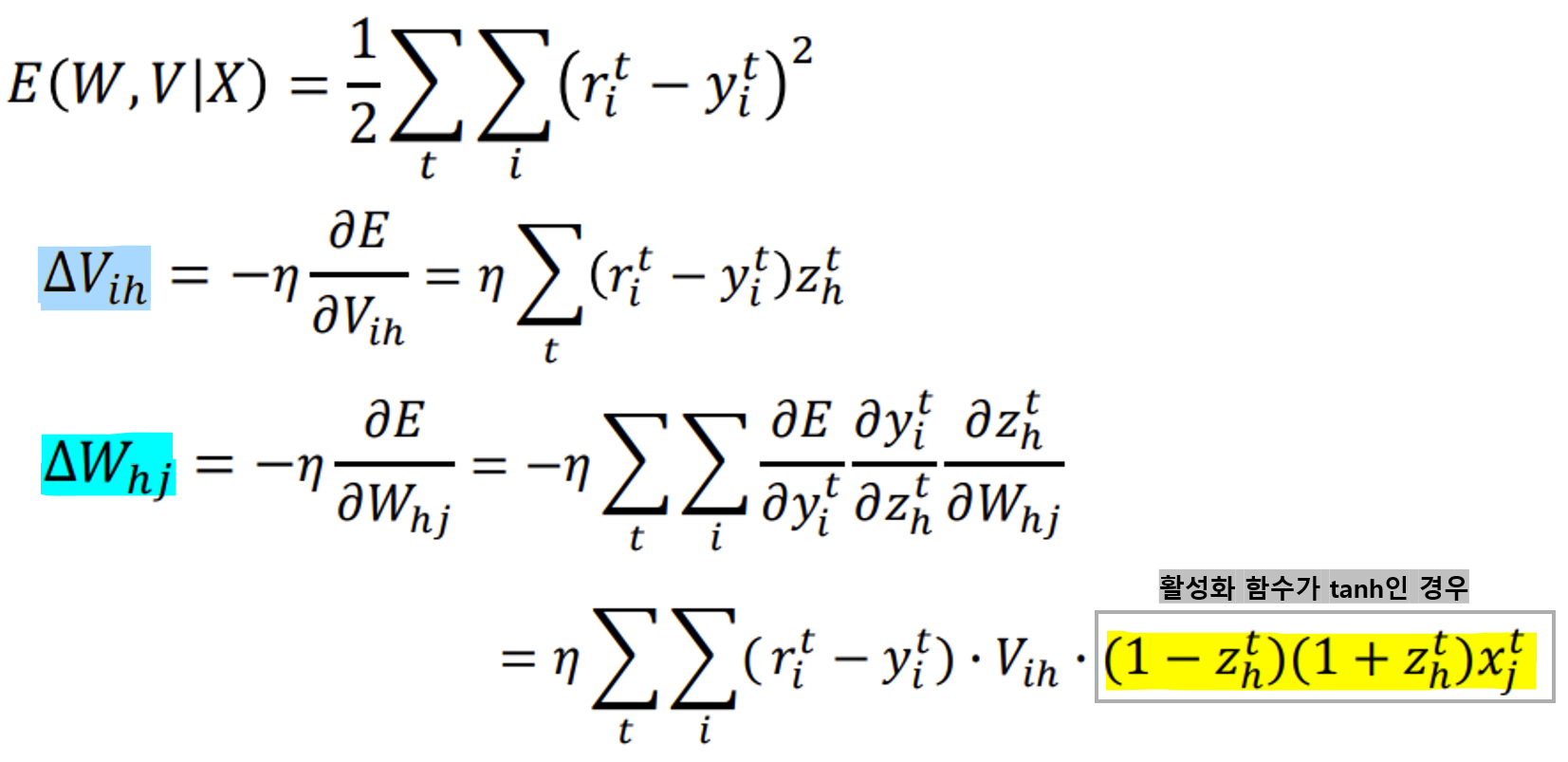
- Error Backpropagation - ReLU

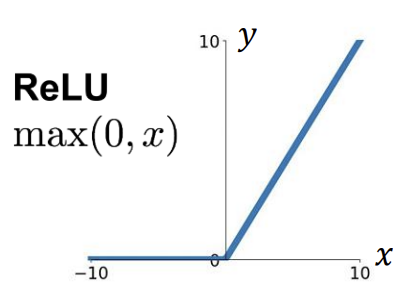
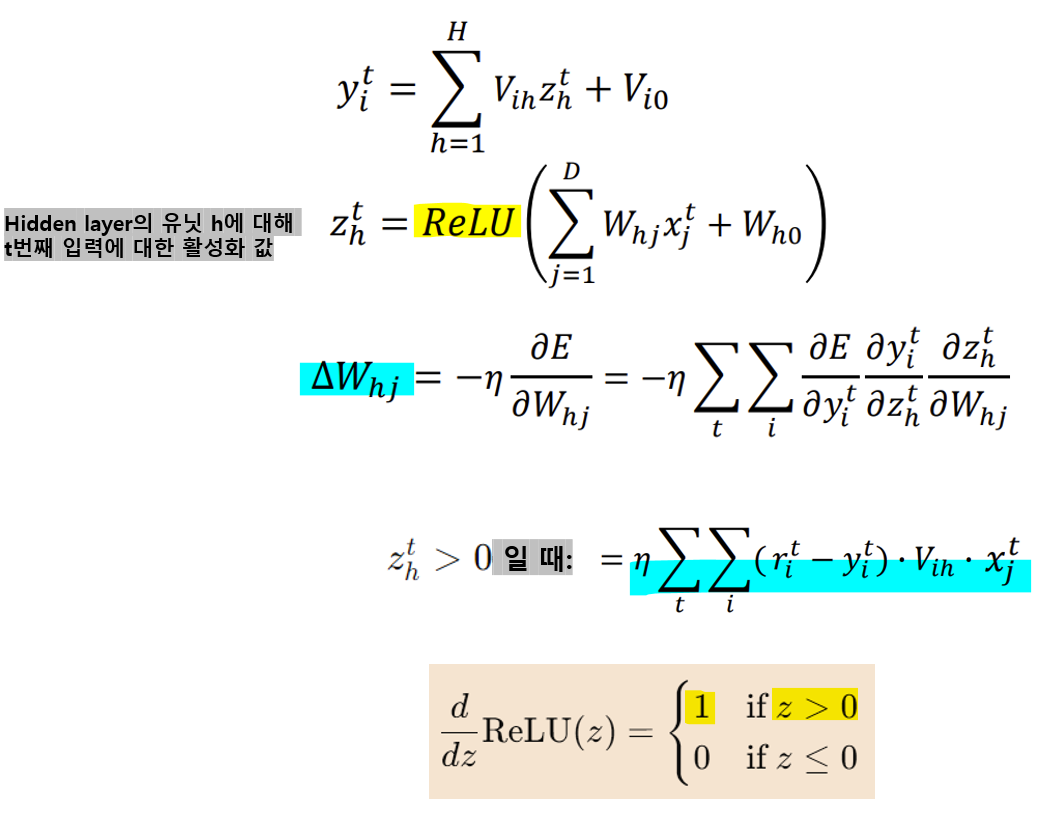
-> ReLU 미분 시, z>0일 때 1이므로 W의 변화량은 위와 같다!

활성화 함수가 출력층에서 항상 필요한 것은 아니며, 출력층에서 사용되는 활성화 함수는 문제의 종류에 따라 다릅니다.

• 회귀 문제: 출력층에서 활성화 함수를 사용하지 않는 경우가 많음. 회귀 문제에서는 출력값이 연속적인 숫자여야 하므로, 굳이 비선형 변환을 적용하지 않고 그대로 출력함. 이 경우 손실 함수로는 보통 평균 제곱 오차(MSE)가 사용됨.
• 분류 문제: 이 경우에는 출력층에서 활성화 함수가 사용됨. 예를 들어, 이진 분류에서는 시그모이드 함수를, 다중 클래스 분류에서는 소프트맥스 함수를 적용해 각 클래스에 대한 확률을 계산함.
  주어진 수식에서, 출력층은 회귀 문제를 해결할 가능성이 높으며, 이 경우 활성화 함수를 적용하지 않고 예측 값을 직접 계산하는 방식으로 이어질 수 있음.

---

- Learning Rate

: 머신러닝 모델이 학습하는 속도를 나타냄

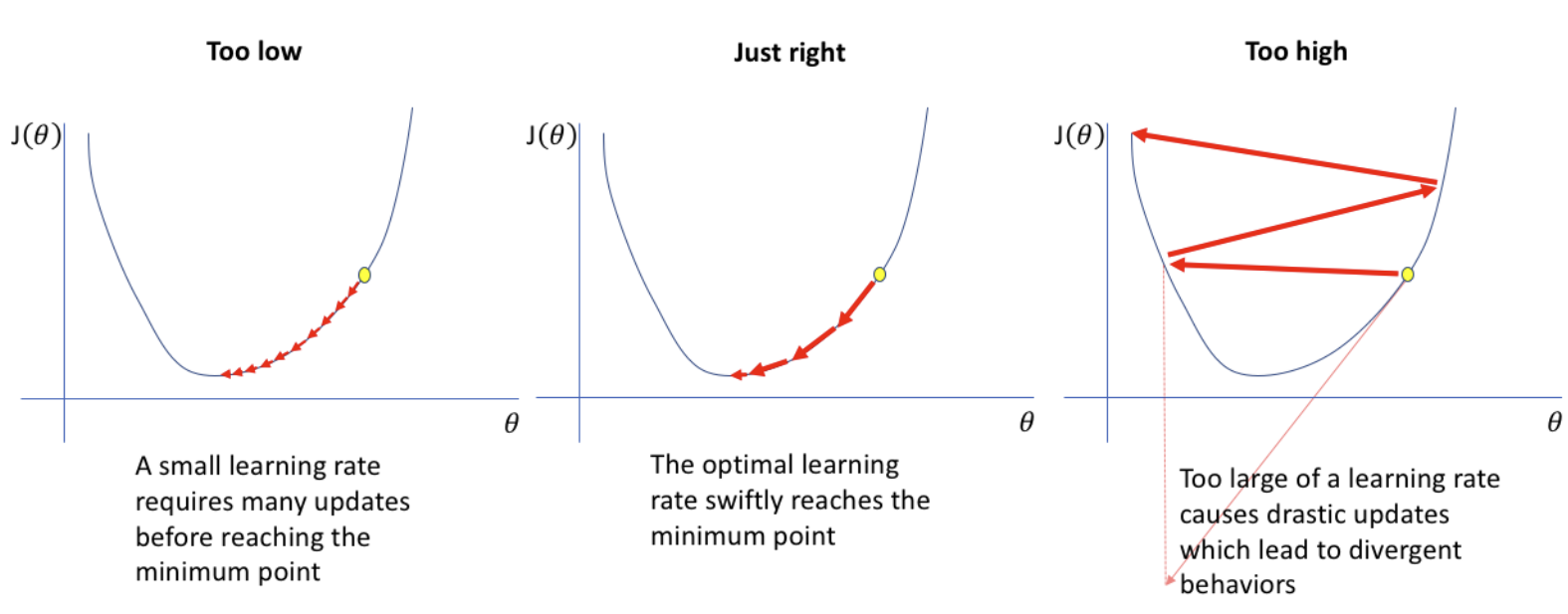
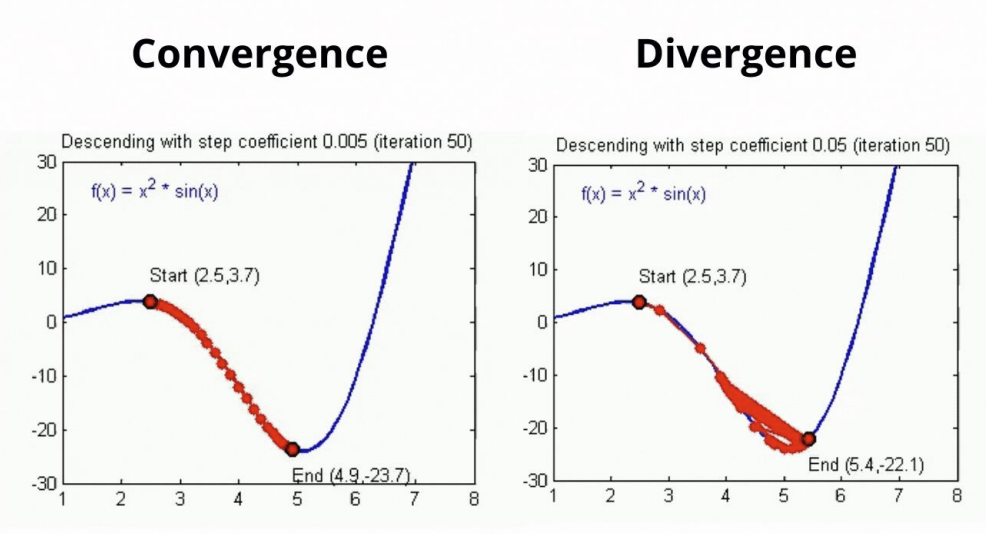
• 초기 단계
  -> 초기 파라미터는 최적 값에서 멀리 떨어져 있으므로 파라미터에 큰 변화를 줘도 OK
  -> Larger learning rate
• 중간 단계
  -> training이 진행됨에 따라 파라미터가 점점 최적 값에 가까워지므로, learning rate을 점차 줄여나감
  -> Learning rate Decay(학습률 감소)
• 최종 단계
  -> training이 끝날 때는 최소값에 수렴하고자 하므로, learning rate을 계속 줄여서 더 작은 변화를 줌

< 1. Step Decay >

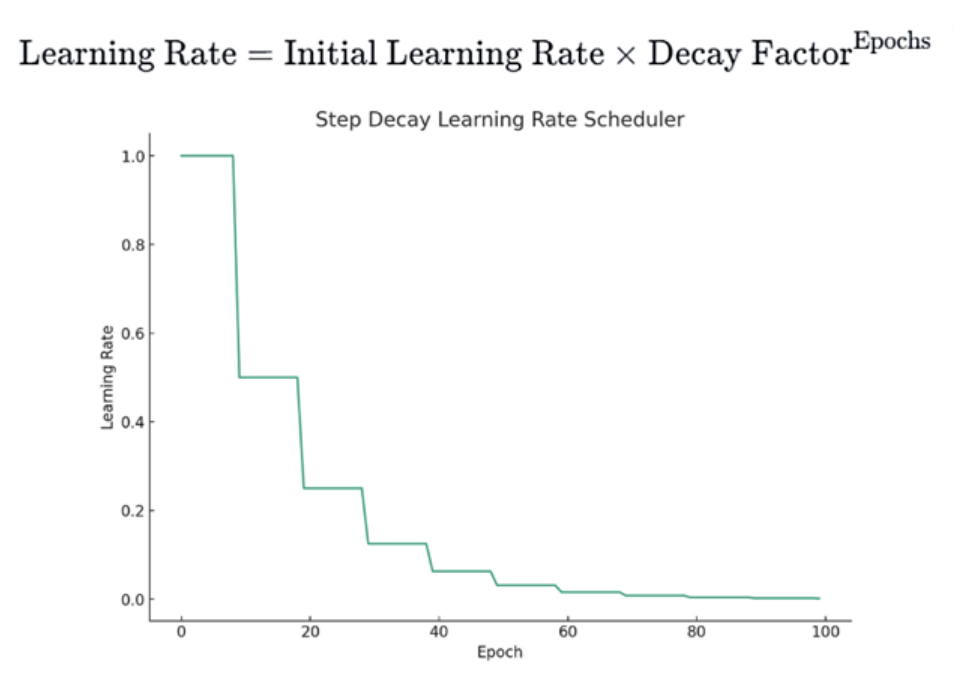
-> 몇 Epoch마다 learning rate을 일정 비율로 감소시키는 방식

< 2. Exponential Decay >

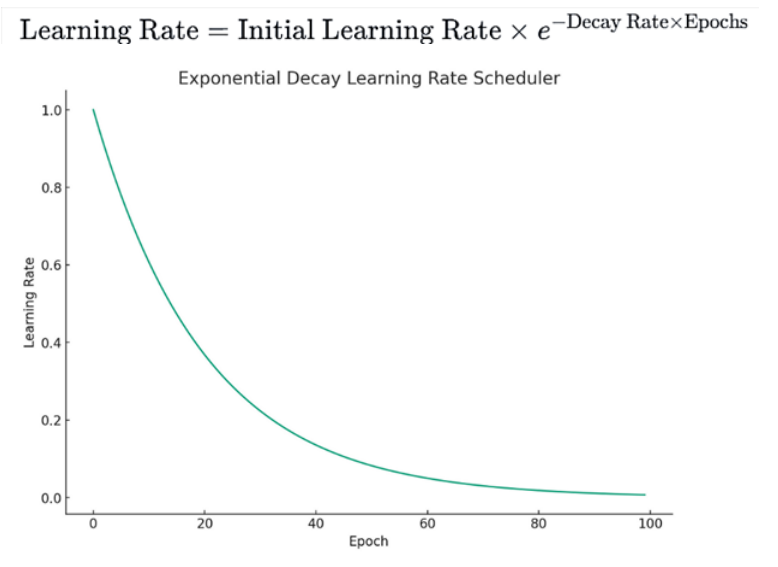
-> 지수 감소 함수를 따르는 방식

---

- Saddle Point

: Cost function의 최적화 지형에서 기울기(gradient)가 0이지만 그 점이 최소값도 최대값도 아닌 특정 지점


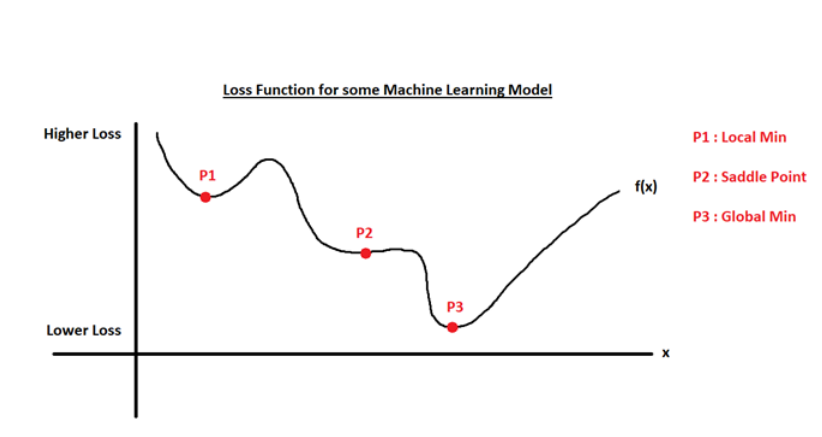
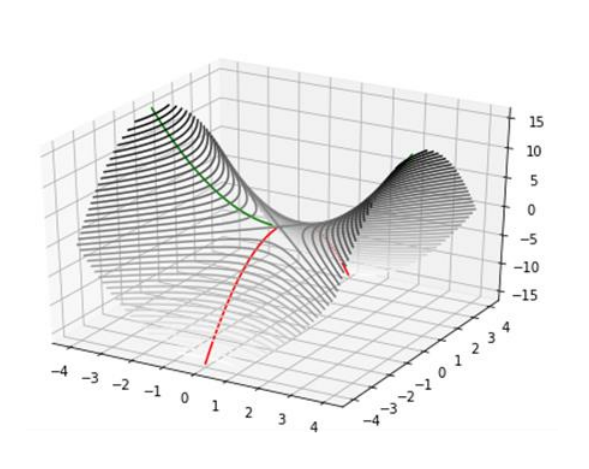
-> 이 점은 Cost function의 표면이 안장 모양을 닮은 지점으로, 일부 차원에서는 위로 휘어지고 다른 차원에서는 아래로 휘어짐
빨간색과 초록색 곡선은 2차원에서 일반적인 안장점에서 교차함
초록색 곡선을 따라 안장점은 local minimum처럼 보이지만, 빨간색 곡선을 따라서는 local maximum처럼 보임

-> Gradient descent는 saddle point에서 매우 느리게 진행됨(기울기가 매우 작아져서)

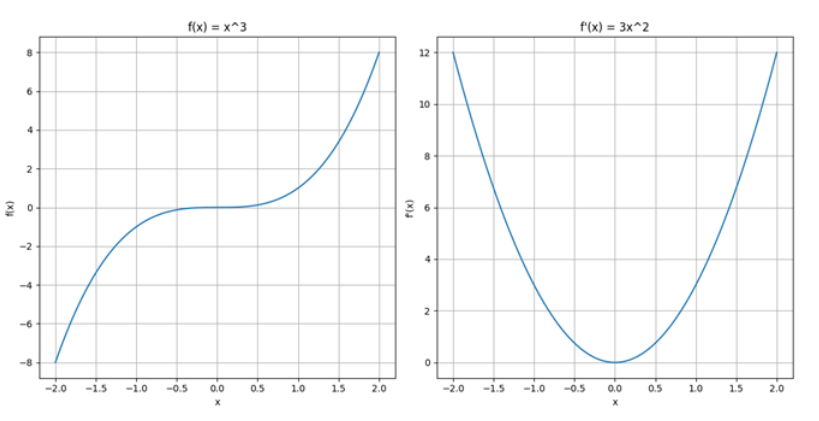
-> 입력값이 매우 크거나 매우 작을 때, 함수가 이러한 극단적인 값에서 포화(saturate)상태에 이르며, 기울기가 거의 0에 가까워짐
-> 이로 인해, 역전파(back propagation) 과정에서 평탄화 현상(plateau effect)이 발생하며, 가중치와 바이어스가 효과적으로 업데이트되지 X

- Deep Learning

* Gradient Vanishing Problem

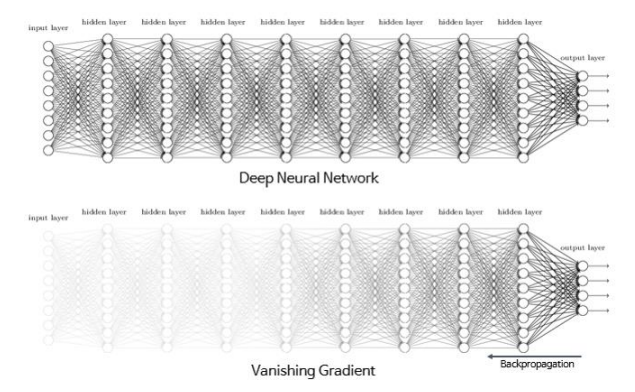
: 신경망 학습 과정에서 기울기가 점점 작아져서 0에 가까워지는 현상, 주로 Deep neural networks에서 발생

- 원인

-> 역전파(Backpropagation) 과정에서 발생, 역전파는 연쇄 법칙(chain rule)을 사용하여 각 층의 기울기를 계산하므로, 기울기는 출력층에서부터 입력층까지 전달되는데, 신경망의 깊이가 깊어질수록 기울기가 계속 곱해지면서 점점 작아질 수 있기 때문!
-> 특히 Sigmoid나 Tanh 같은 비선형 활성화 함수를 사용할 때
-Sigmoid 함수: 출력 범위가 0에서 1 사이이기 때문에, 입력이 매우 크거나 작을 때 출력이 포화(saturate) 상태에 도달하여 기울기 값이 매우 작아짐
-Tanh 함수: 출력 범위가 −1에서 1 사이이므로, 입력이 극단적인 경우 기울기 값이 작아지는 포화 상태가 발생할 수 있음

- 해결 방법

1) ReLU (Rectified Linear Unit) 사용: ReLU 함수는 입력이 양수일 때 기울기가 1이므로, 기울기가 소실되지 않고 깊은 네트워크에서도 학습이 잘 이루어짐

2) 가중치 초기화 기법: He 초기화나 Xavier 초기화와 같은 가중치 초기화 기법은 네트워크 초기 단계에서 기울기 소실 문제를 줄이는 데 도움됨

3) 배치 정규화(Batch Normalization): 각 층의 입력을 정규화함. 배치 정규화는 신경망의 각 층에서 입력 값의 분포를 조정해 학습이 안정적이도록 만듦

4) 심층 신경망의 대체 구조: LSTM(Long Short-Term Memory)이나 GRU(Gated Recurrent Unit)와 같은 구조는 기울기 소실 문제를 완화할 수 있는 설계로, 주로 순환 신경망(RNN)에서 사용됨

* AlexNet

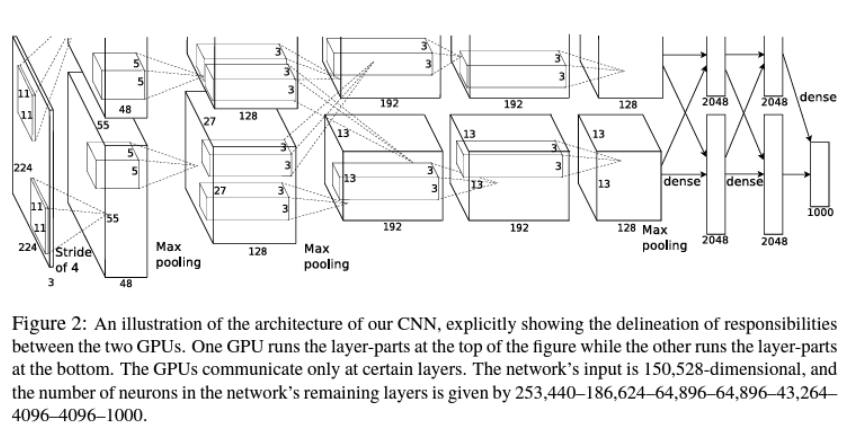
: 딥러닝 기반의 합성곱 신경망(CNN)
: Convolution Layer (5)+ Fully-Connected Layer (2) + Classification

* CNN (Convolutional Neural Network), 합성곱 신경망

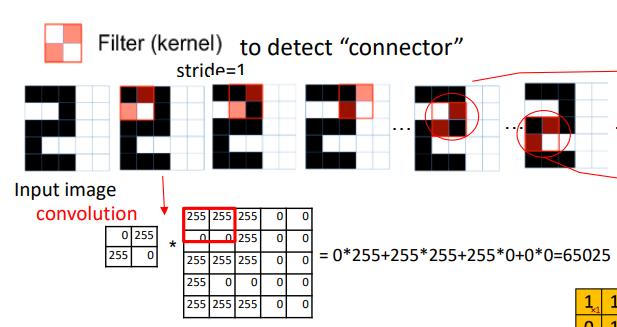
: CNN은 필터를 왼쪽 위에서 오른쪽 아래로 슬라이딩하며 이미지에서 특징을 추출함

• Filter(혹은 Kernel) : Feature를 식별하는 역할
• Stride : 필터가 한 방향으로 한 번에 이동하는 거리(필터가 매 단계에서 얼마나 많이 이동하는지)
• Receptive Field(수용 영역) : 필터가 위치하는 영역(필터가 현재 살펴보는 이미지의 특정 부분을 의미)

* Dying ReLU Problem

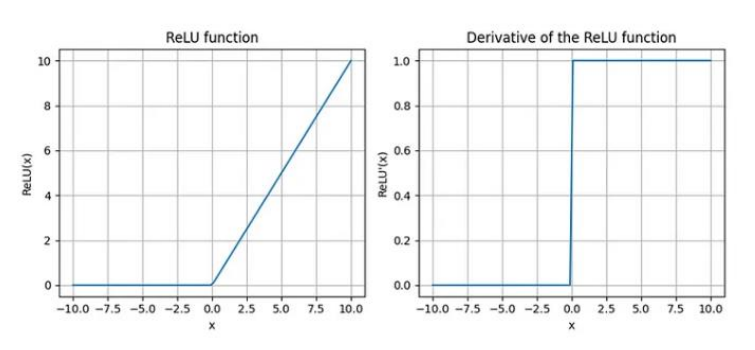
-> 제한점 : Dying ReLU 문제 -> 입력에 대해 0을 출력하기 시작하면, 뉴런이 더 이상 학습하지 않음

* Leaky ReLU (Leaky Rectified Linear Unit)

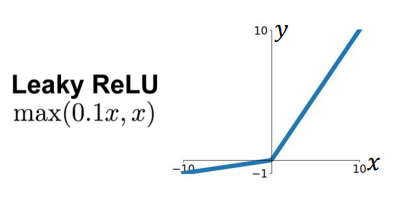
: ReLU 기반의 활성화 함수로, 음수 값에 대해 작은 기울기를 가짐
-> Dying ReLU 문제를 완화함!
: 이 작은 기울기의 계수는 훈련 전에 미리 정해지며, 훈련 중에 학습되지 X
: sparse gradients(희소한 기울기) 문제*를 겪을 수 있는 작업에서 많이 사용되는 활성화 함수

• Sparse Gradient Problem : 주로 ReLU와 같은 함수에서 음수 입력에 대해 기울기가 0이 되는 상황에서 발생하고, 이로 인해 신경망의 일부 뉴런들이 죽어(Dying ReLU) 기여하지 않게 되는 현상

* Dropout

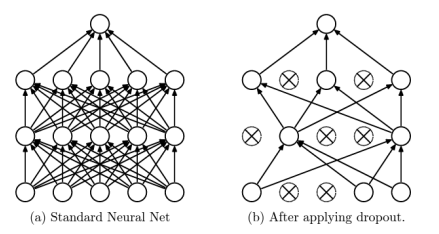
: 훈련 중에 신경망의 유닛(노드)와 그 연결을 무작위로 제거함
-> Overfitting을 크게 줄여줌, 다른 정규화 방법들에 비해 큰 성능 향상을 제공함
-> 신경망이 훈련 중 특정 유닛에 과도하게 의존하는 것을 막아서 모델이 더 일반화된 형태로 학습되도록 함

* Epoch

: 신경망을 전체 훈련 데이터로 한 번 훈련시키는 주기
: 하나 이상의 배치(Batch)로 구성됨

* Batch : 신경망 훈련 시 한 번에 처리하는 데이터 샘플의 묶음

-> 전체 데이터셋을 1번 돌면 1 epoch!

* Iteration : Batch 에 있는 traning example을 처리하는 것

• 역전파 과정은 Batch 단위로 수행됨

• 평균 제곱 오차(MSE)나 교차 엔트로피(Cross-entrophy)가 역전파 과정에 사용됨

• Gradient descent 알고리즘에서는 역전파 과정 중 모든 뉴런의 활성화 결과가 필요하므로, GPU 메모리가 많이 사용됨
  -> GPU 메모리가 작기 때문에 training data를 나눠서 시킴(여러 batch로)