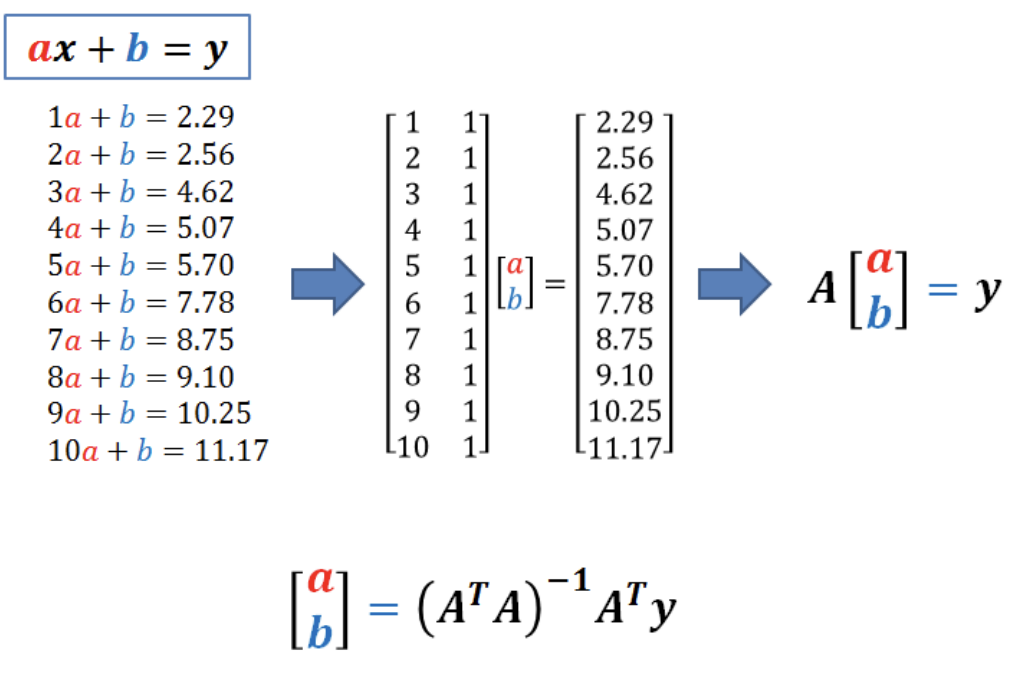
- Feature = 1일때 가설함수
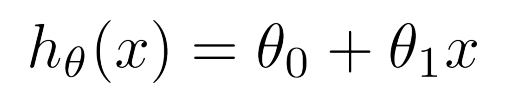
< Multiple Variables>
- Feature = 4일때 가설함수 (n = 4)
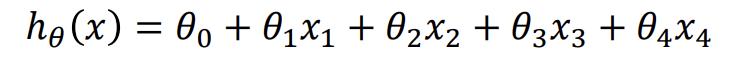
- Multivariate Linear regression
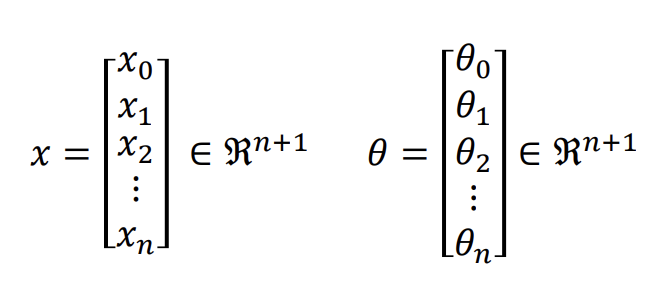
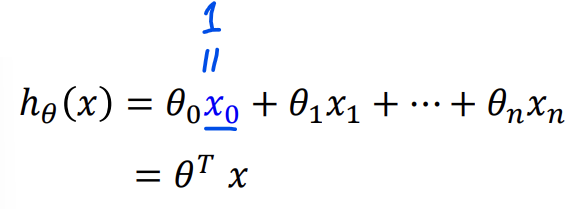
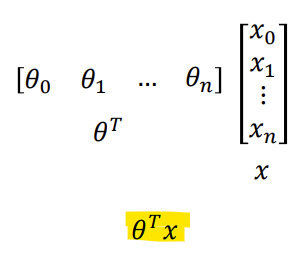
-> 계산 편의를 위해 x0 = 1을 추가함
- Gradient descent for multiple variables


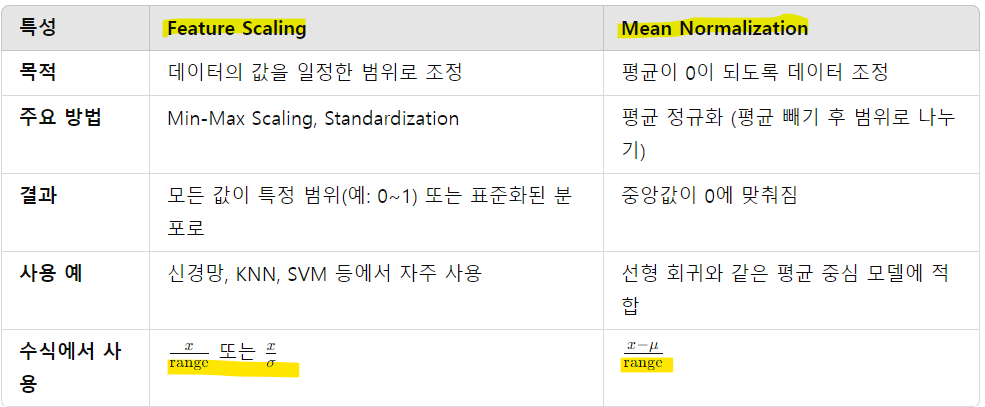
- Feature Scaling
- normalization하지 않으면 각 변수마다 범위가 달라서 특정 변수에 민감해짐
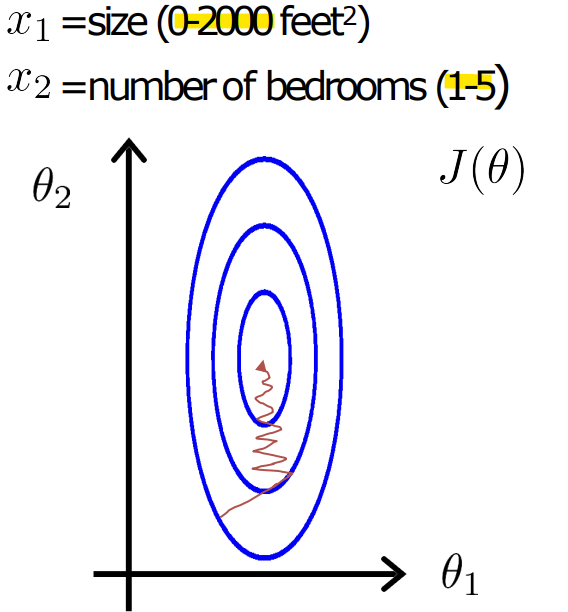
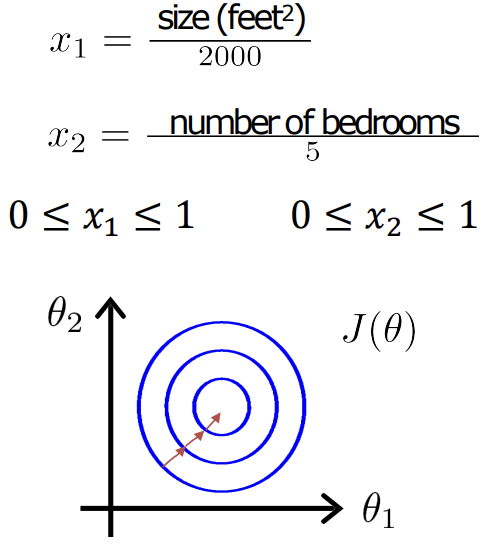
- 이상적인 범위
: -1 ~ 1
: -3 ~ 3
: -1/3 ~ 1/3
ex)
0 <= x <= 3 : 괜찮음
-2 <= x <= 0.5 : 괜찮음
-100 <= x <= 100 : scaling 필요
-0.0001 <= x <= 0.0001 : scaling 필요
* Mean normalization
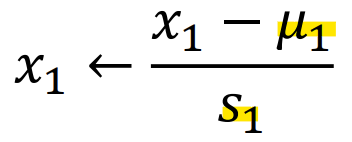
-> u는 평균
-> S는 범위(최대값 - 최소값) 혹은 표준편차(Standard deviation)
(x - 평균) / 표준편차 로 normalization
-> x0에는 normalization하면 안 됨
-> Training할 때 적용한 normalization은 Test할 때도 꼭 해줘야 함!
- Learning rate
- Gradient descent
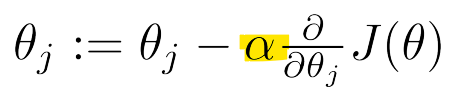
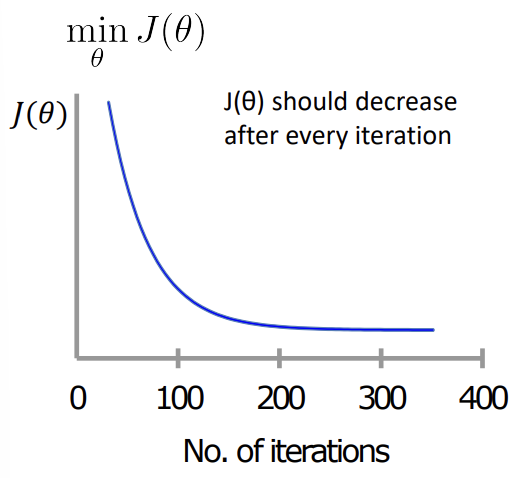
- J가 발산(diverge)하는 경우
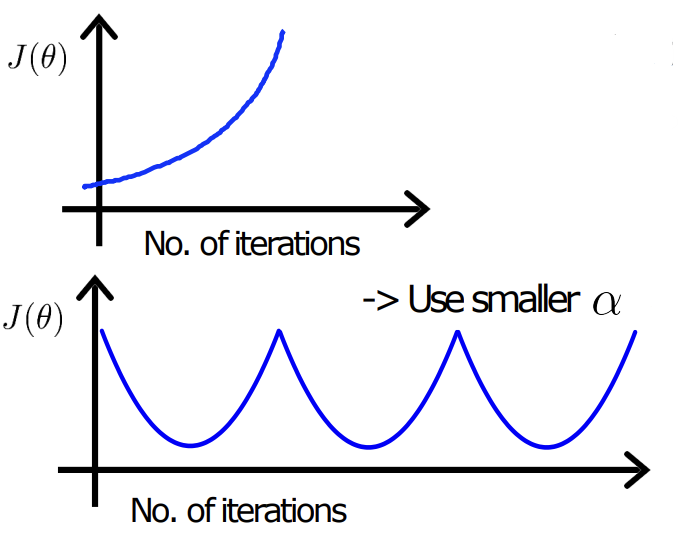
-> learning rate 줄이기
- learning rate가 너무 작으면, converge(수렴)까지 너무 느림
-
learning rate와 theta를 학습으로 구하려면 -> divide and conquer로 하나씩 구하면 됨
-
learning rate은 보통 0.001, 0.01, 0.1, 1 중에서 선택
- Features and polynomial regression
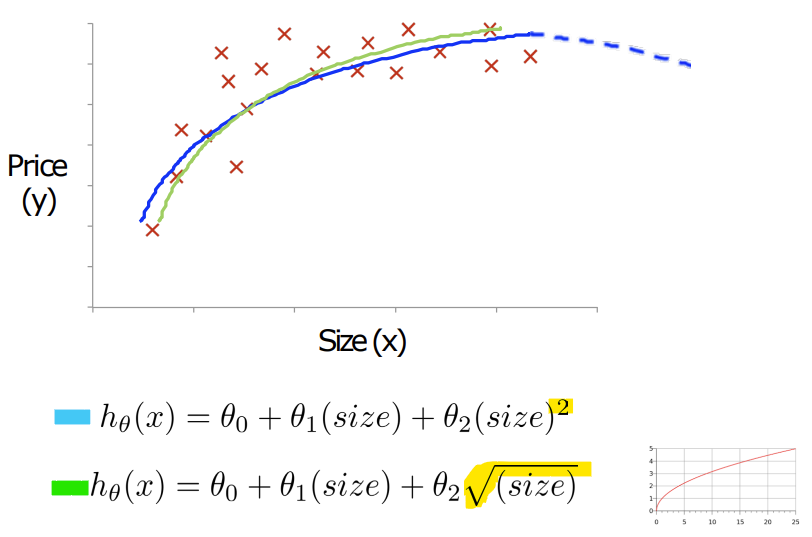
- Polynomial Regression, 다항 회귀
-> Dimension Extension을 통해 다항식 형태로 모델링
-> 데이터가 선형 회귀 모델로 적합하지 않을 때 (데이터가 곡선 형태로 분포할 경우 사용)
-> 주택 가격, 주식 시장 분석, 또는 날씨 변화 등 비선형적인 패턴을 학습할 때 적합
- Linear regression: 직선
- Polynomial regression: 곡선
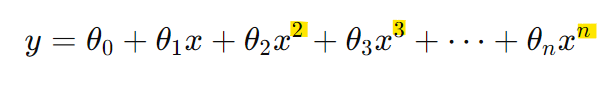
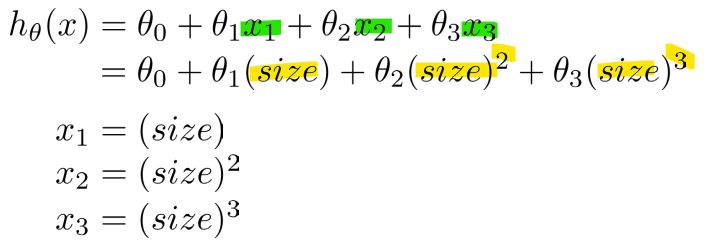
-> 위 식: 새로운 feature data x2, x3를 추가
-> 아래 식: 하나의 feature로 dimension을 증가시킴 (1차 -> 3차)
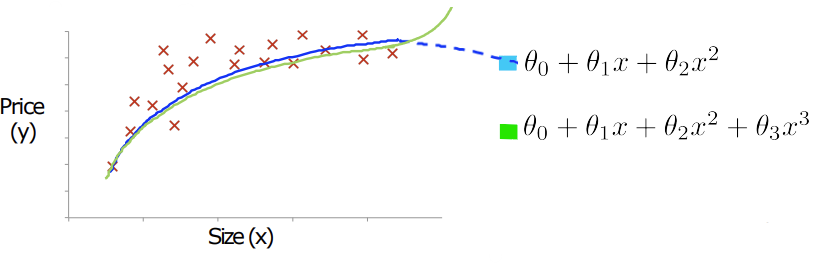
* Dimension extension, 차원 확장
- 장점: error가 감소됨
- 단점: overfitting될 가능성 증가, 차원이 증가하면 계산 복잡도가 커지고, 데이터가 부족할 경우 학습 성능이 떨어질 수 있음
- 주의할 점: dimension extension에 따라서 Feature Scaling해줘야 함
<여러 개의 feature가 있을 때의 polynomial regression>

- Normal equation(vs Gradient descent)
* Normal equation, 정규 방정식
: Linear regression에서 비용 함수를 최적화하여 최적의 매개변수(theta)를 계산하는 해석적 방법(Analytical Solution)
-> 경사 하강법과 달리, 반복 과정을 거치지 않고 한 번에 최적의 해를 구함
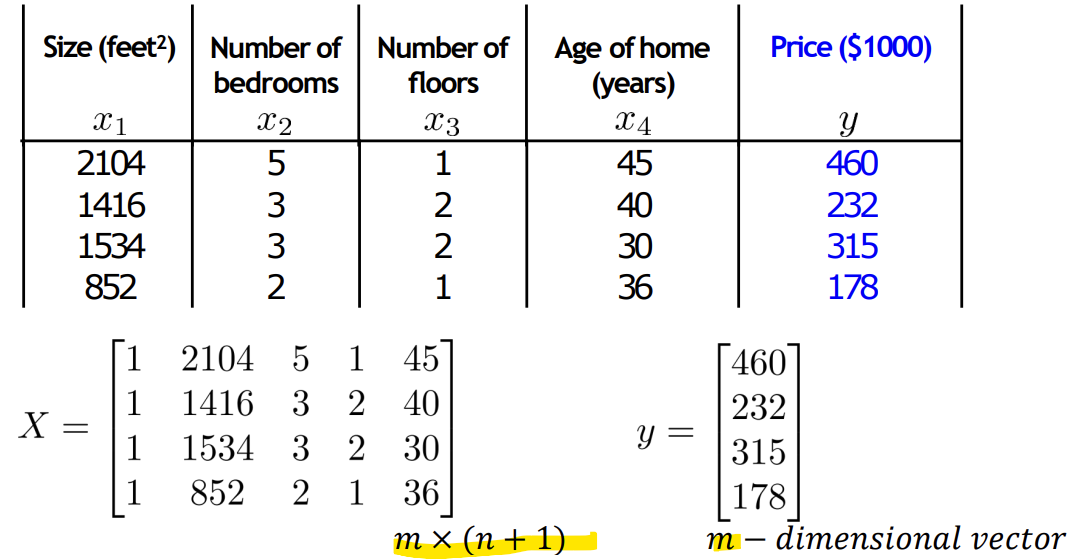

-> 식 유도과정
-> m은 무시되므로 n에 dependency가 있음

- 매트랩의 inverse 함수 사용
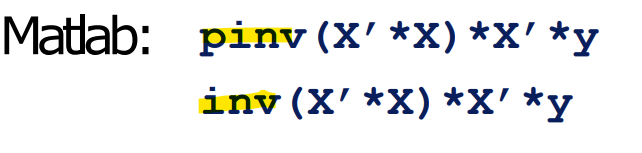
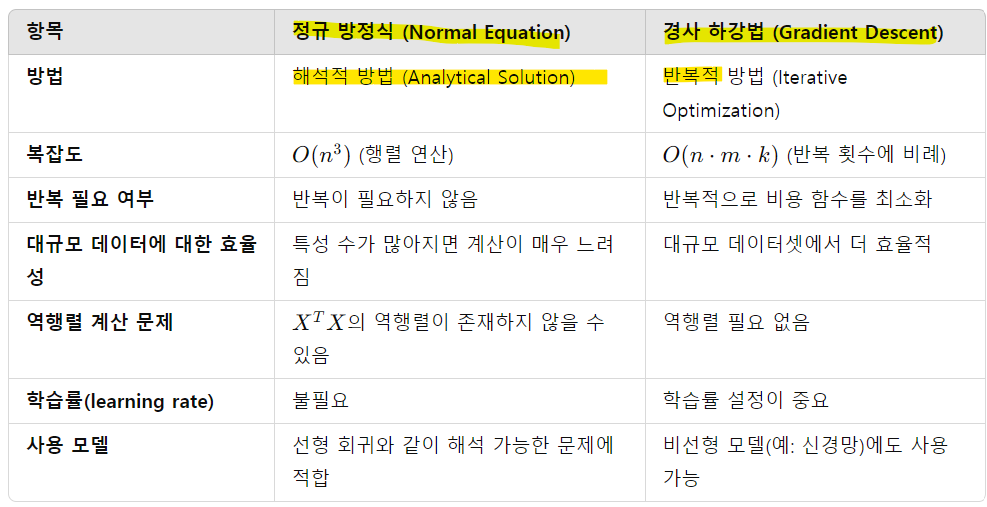
-> Normal Equation은 대규모 데이터 및 특성 수가 많은 경우에는 적합하지 X
-> Gradient descent는 start point에 따라 결과가 달라짐, GPU에 최적화됨
-> Normal Equation에서 m은 뭉게지고 n만 남기 때문에 n에 의해 속도가 느려짐, 결과가 항상 일정함
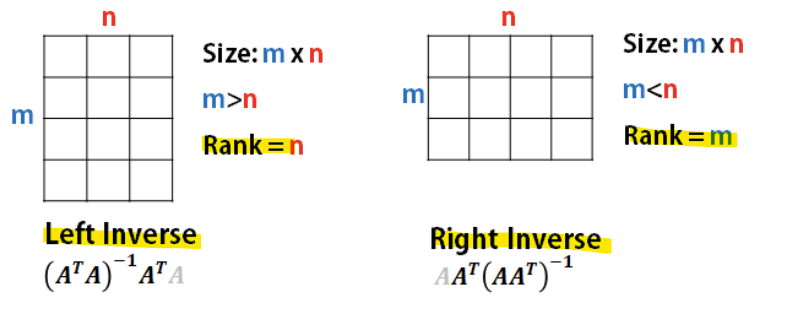
-> m < n인 경우(sample 수가 feature 수보다 적은 경우) Singularity 문제 발생
-> XT*X 행렬이 역행렬을 구할 수 없는 단수 행렬(singular matrix)이 됨