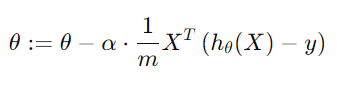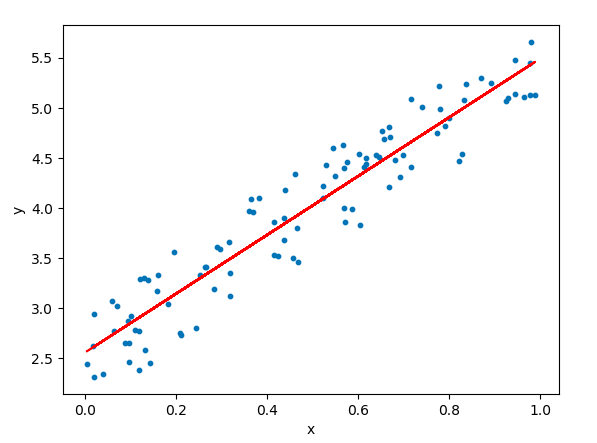
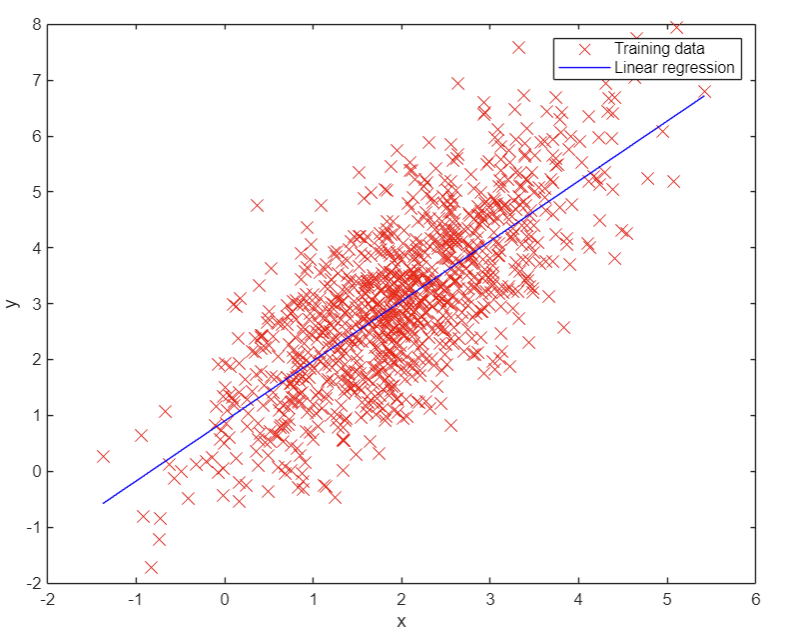
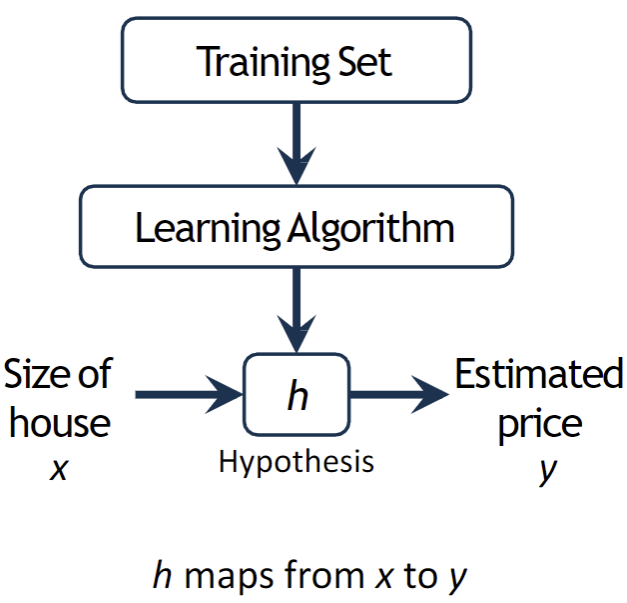
가설함수(hypothesis function) h에 x값을 넣으면 예측값 y가 나옴
1. 선형 회귀 모델의 가설 함수
* 가설 함수 : 입력 데이터에 대한 예측을 수행하는 함수
1) 다중 선형 회귀 모델의 가설 함수
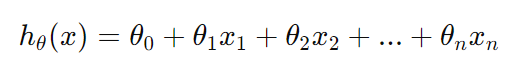

위 함수를 간단하게 벡터 형태로 표현 시,
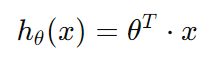

2) 단순 선형 회귀의 가설 함수
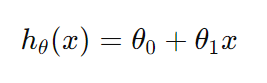

하나의 독립 변수만 있을 경우 사용됨
* 가중치 (Weights)
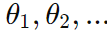
: 각 입력 변수 x1, x2, ...가 종속 변수 y에 얼마나 큰 영향을 미치는지를 나타냄
-> 가중치가 클수록 해당 입력 변수는 예측값에 더 큰 영향을 줌!
2. 비용 함수 (Cost Function)
https://www.kdnuggets.com/2020/05/5-concepts-gradient-descent-cost-function.html
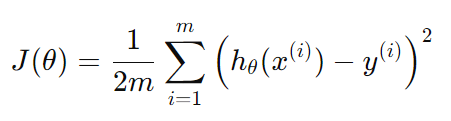

: 비용 함수(손실 함수)는 보통 평균 제곱 오차(MSE, Mean Squared Error)로 정의되며, 가설 함수가 반환한 예측값과 실제 값의 차이 제곱의 합으로 구함
-> 비용 함수 J 의 값을 최소화하는 방향으로 가설 함수의 theta값을 조정하는 것이 학습의 목표!
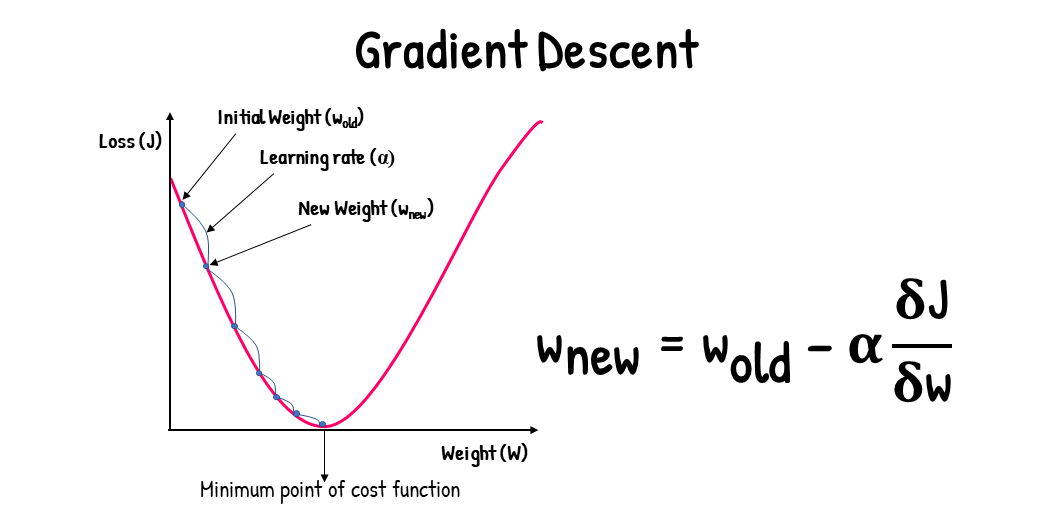
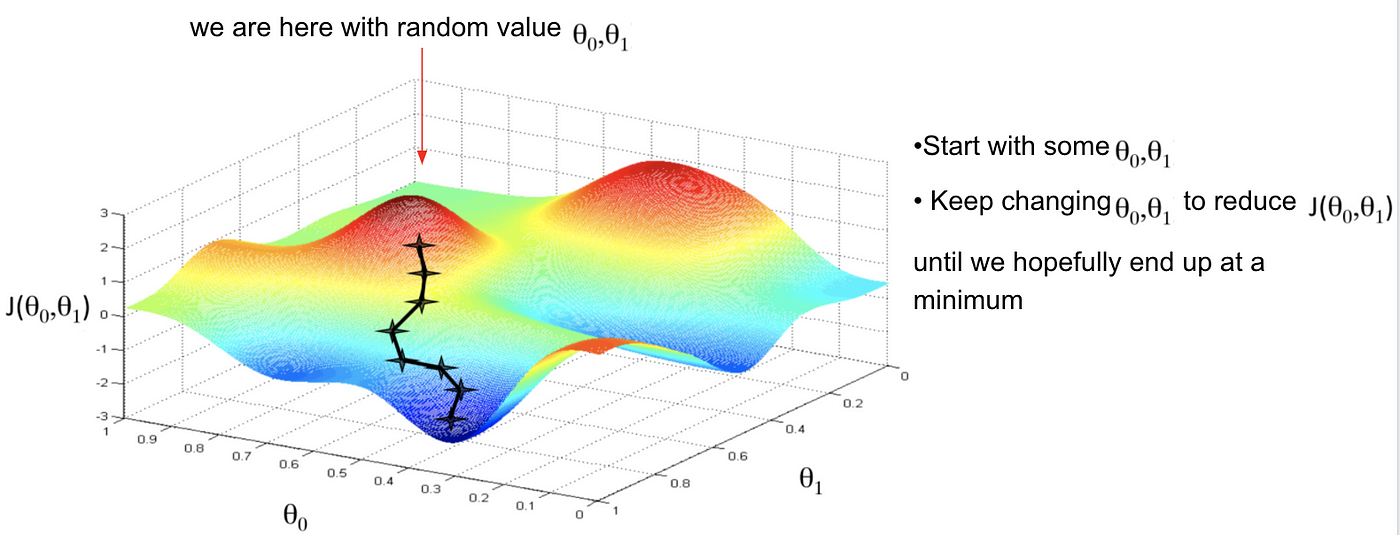
3. 경사 하강법 (Gradient Descent)
: 머신러닝 및 딥러닝에서 최적화 알고리즘으로 사용되는 방법
: 비용 함수의 기울기(Gradient)를 계산하고, 그 기울기를 따라가며 비용 함수의 최소값을 찾는 알고리즘
모델의 비용 함수를 최소화하는 데 사용됨 -> 모델의 가중치(theta)를 최적의 값으로 업데이트 함!
<경사 하강법의 과정>
1) 초기화
: 가중치 theta를 임의의 값(0 또는 난수)로 설정
2) 비용 함수 계산
: 현재 theta값으로 비용 함수 J를 계산
3) 기울기 계산
: 현재 theta값에서 비용 함수의 기울기를 계산
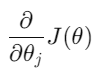
-> 비용 함수 J에 대한 기울기는 각 가중치 theta j 에 대한 편미분으로 계산함
4) 가중치 업데이트
: theta는 기울기가 가리키는 방향으로 업데이트
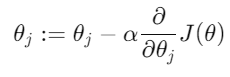
J의 기울기를 계산하여 대입하면,
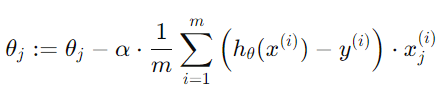
* 벡터화된 가중치 업데이트 공식
-> 실제 코드 구현 시 해당 과정을 벡터화하여 한 번에 계산함

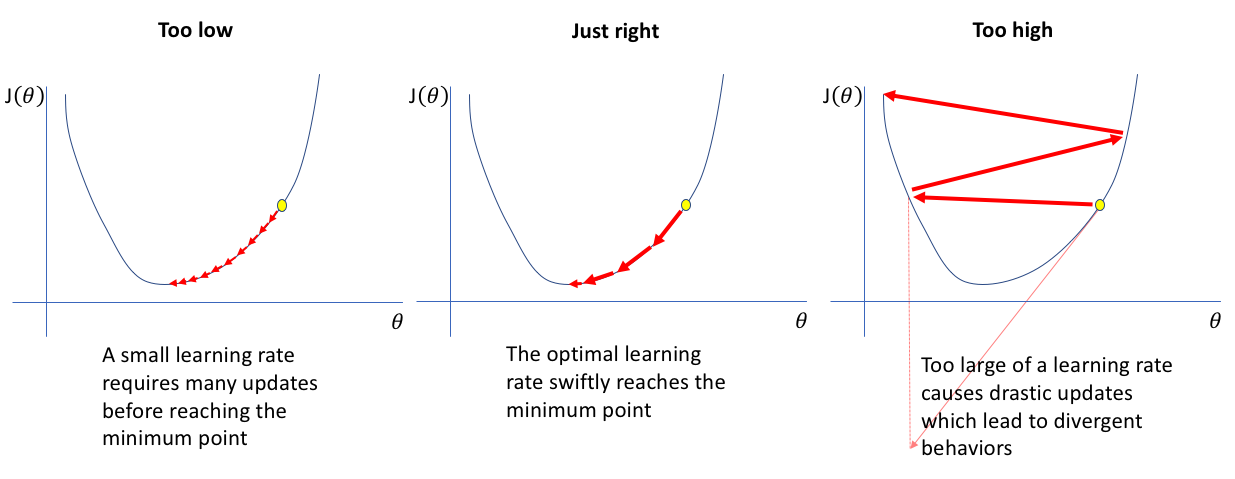
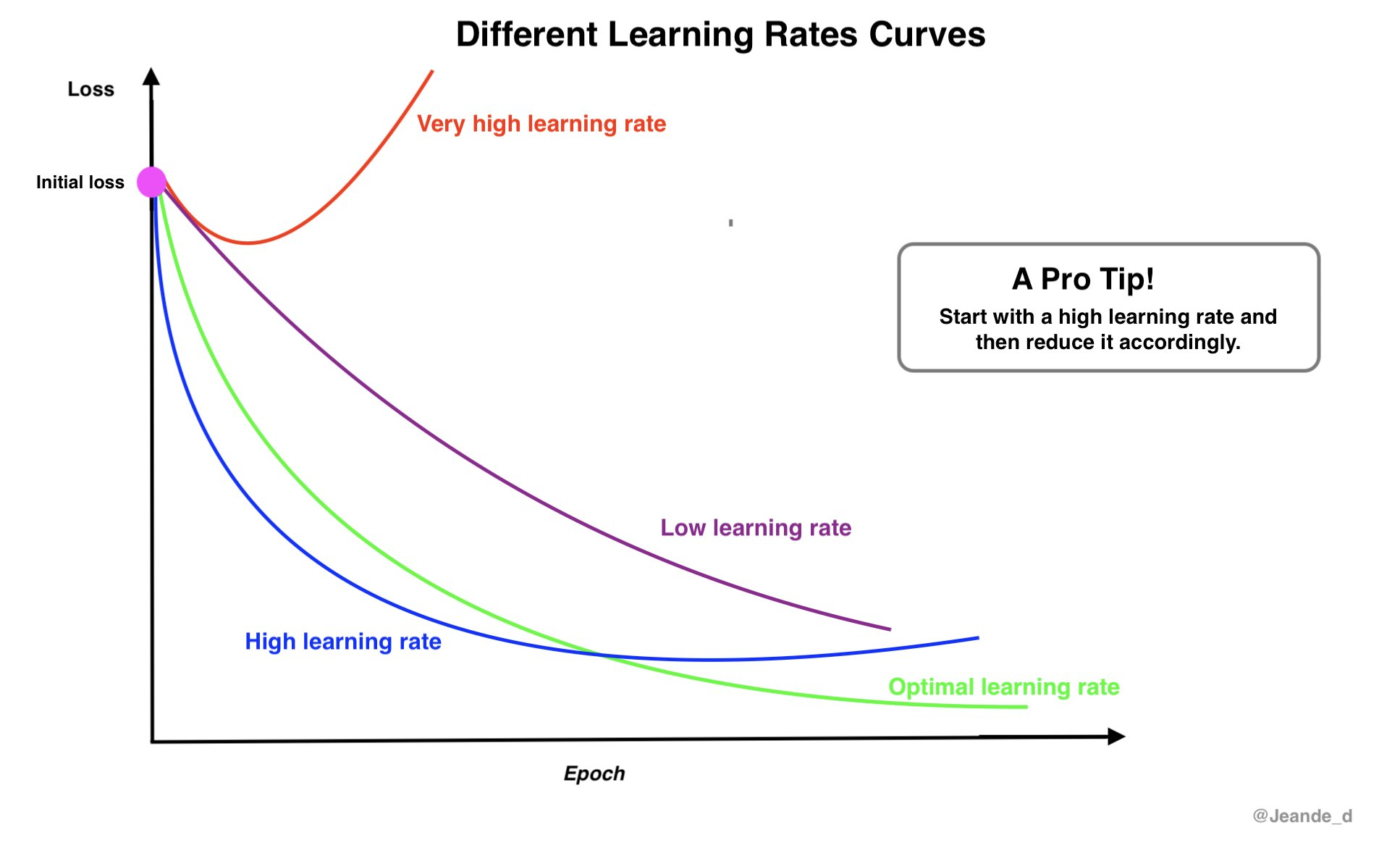
* 학습률(Learning Rate)
: 위 업데이트 수식에서의 alpha값은 Learning Rate로, 한 번의 업데이트에서 가중치를 얼마나 변경할지를 결정함
https://www.jeremyjordan.me/nn-learning-rate/
5) 반복
: 비용 함수가 더 이상 감소하지 않거나, 기울기가 매우 작아져서 가중치 theta의 변화가 작아질 때까지 위 과정을 반복
<경사 하강법의 유형>
1) 배치 경사하강법(Batch Gradient Descent)
: 전체 데이터셋을 사용하여 기울기를 계산하고 파라미터를 업데이트함
2) 확률적 경사하강법(Stochastic Gradient Descent, SGD)
: 하나의 데이터 포인트에 대해 기울기를 계산하고 즉시 파라미터를 업데이트함
3) 미니배치 경사하강법(Mini-batch Gradient Descent)
: 데이터셋을 작은 배치로 나눠, 각 배치에 대해 기울기를 계산하고 파라미터를 업데이트함
* 배치(Batch) : 데이터를 처리하는 단위
-> 모든 데이터셋을 한번에 처리하면 메모리 사용량이 매우 커지므로, 데이터셋을 작은 배치로 나누어 처리하여 성능을 향상시킴
- 작은 배치 크기 : 가중치 업데이트가 자주 되어 더 빠르게 수렴됨 / But, 기울기 불안정
- 큰 배치 크기 : 기울기 더 정확 / But, 메모리 사용량 많고 학습 속도 느림