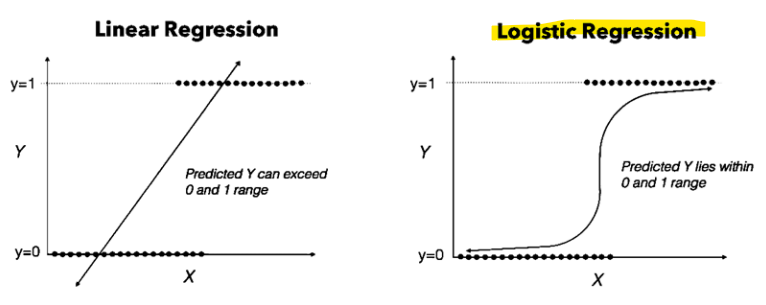
- Hypothesis Representation
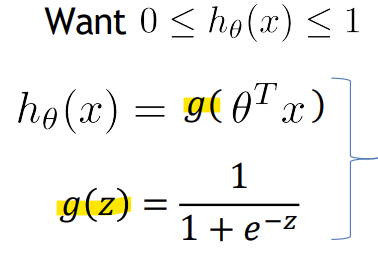
-> 활성화 함수 중 Sigmoid (= Logistic) function을 사용
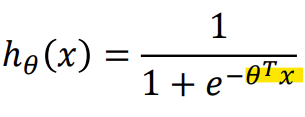
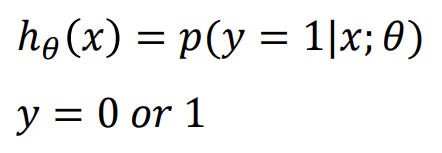
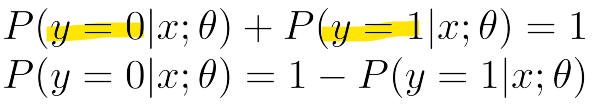
-> y = 0일 확률 + y = 1일 확률의 합은 1
- Decision boundary
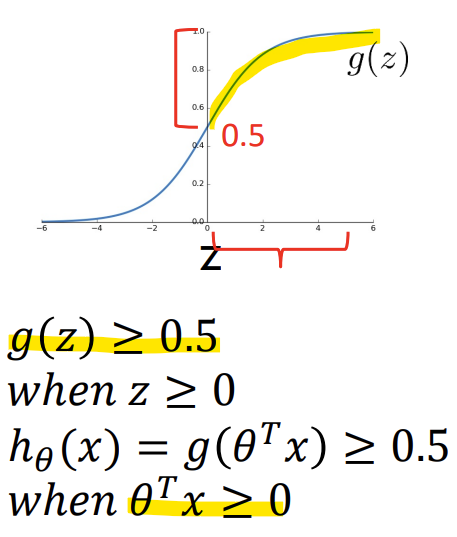
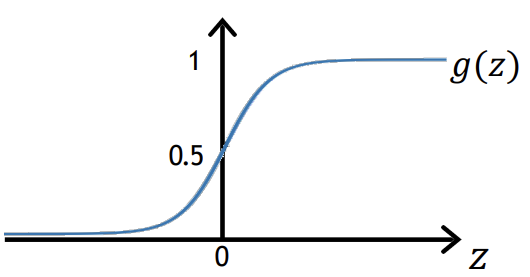
-> z가 0보다 크거나 같을 때 g(z)가 0.5보다 크거나 같음
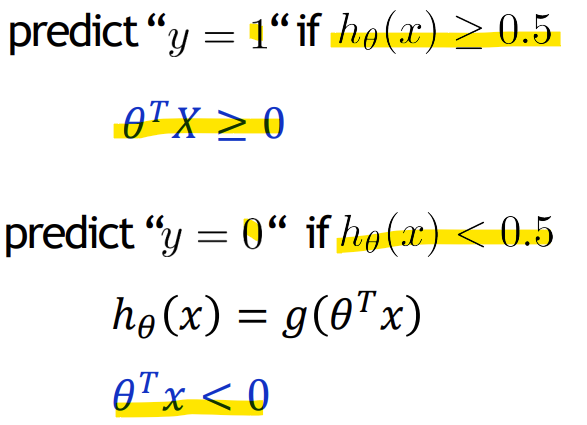
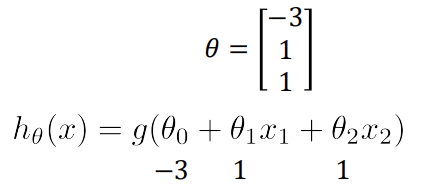
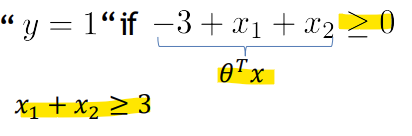
-> x1 + x2 >= 3의 경우, y = 1
-> x1 + x2 < 3의 경우, y = 0이 됨
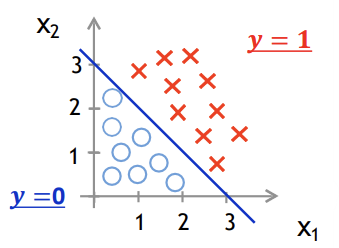
-> x1 + x2 = 3이 Decision boundary가 됨
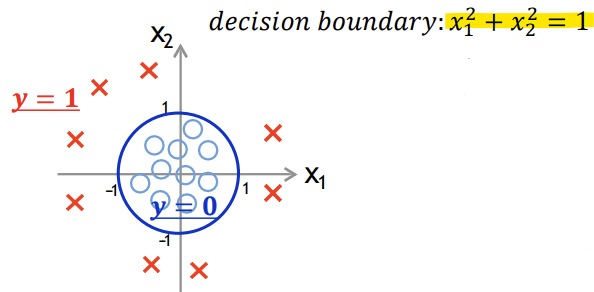
- Non-linear decision boundaries
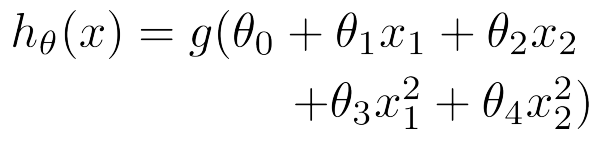
-> Polynomial regression
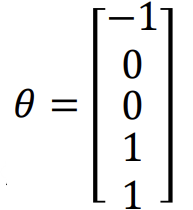
theta값을 식에 대입 시
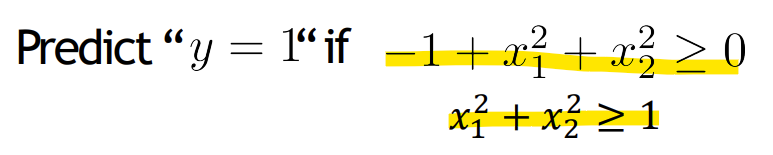
- Cost function
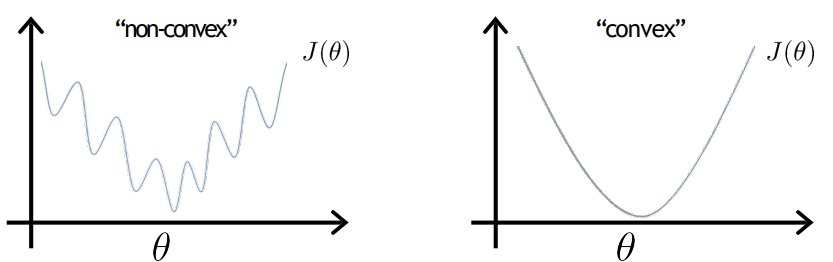
- Convex: 곡선이 아래로 볼록하거나 함수의 최솟값이 하나만 존재하는 상태
- Logistic regression cost function
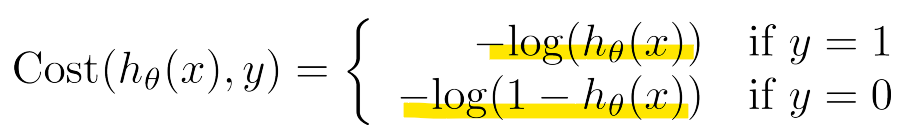
-
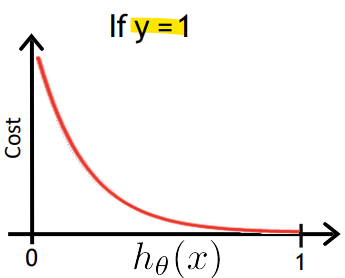
y = 1인 경우
: 예측 값 h(x)가 1에 가까울수록 손실이 0에 가까워짐
: 예측 값이 0에 가까워질수록(잘못된 예측) 손실이 커져 무한대에 수렴함
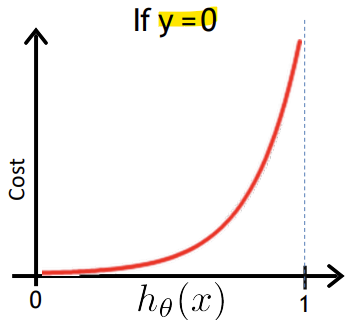
-
y = 0인 경우
: 예측 값 h(x)가 0에 가까울수록 손실이 0에 가까워짐
: 예측 값이 1에 가까워질수록(잘못된 예측) 손실이 무한대로 증가함
-> 잘못된 예측에 대해 큰 페널티를 부과하여 모델이 정확한 예측을 하도록 강제함
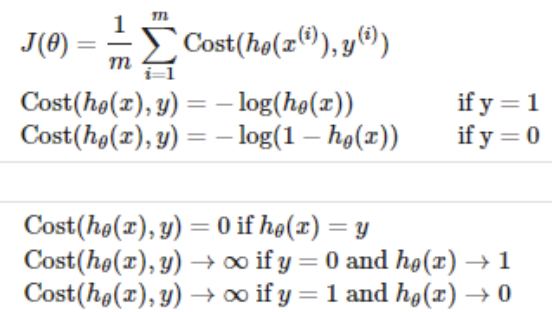
- Simplified cost function and gradient descent
- Logistic regression cost function
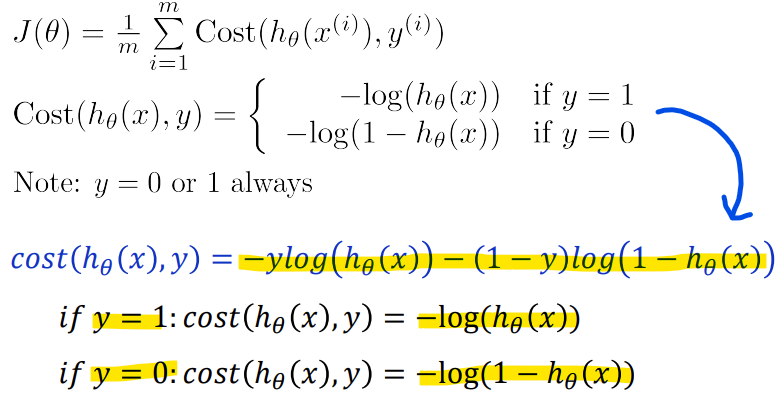
-> y = 0이거나 y = 1뿐이므로 하나의 식으로 합칠 수 있음(linear가 아닌 classification이라서)
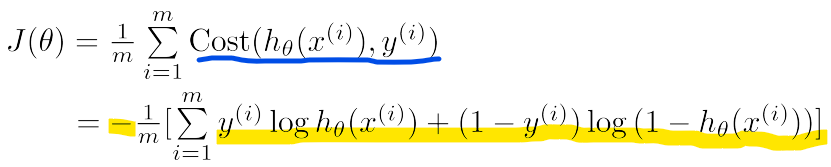
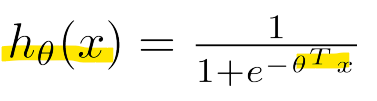
- Gradient descent
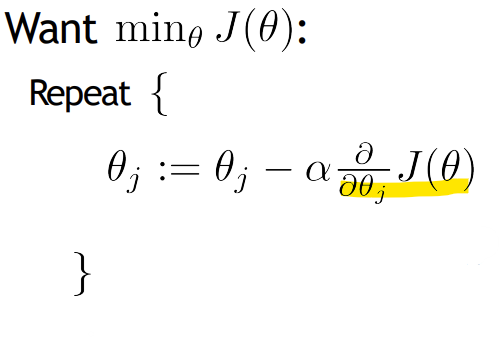
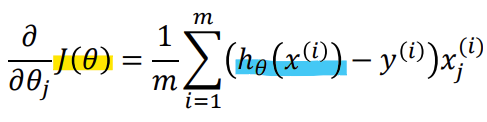
-> Logistic regression 의 J(theta)의 미분한 식이 Linear regression 과 동일함!
-> 개별 Cost function과 가설함수(h(x))만 다름
- J(theta): 모델 전체에 대한 평균 비용을 나타내는 Cost Function
- Cost(h(x), y): 하나의 샘플에 대한 손실을 측정하는 개별 Cost function
-
Sigmoid function의 미분 유도과정
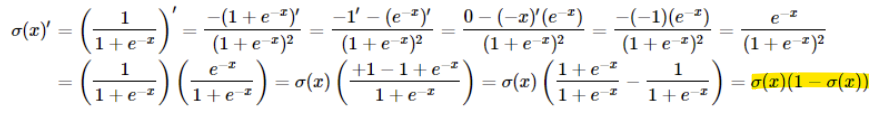
-
logistic regression의 Cost function 미분 과정
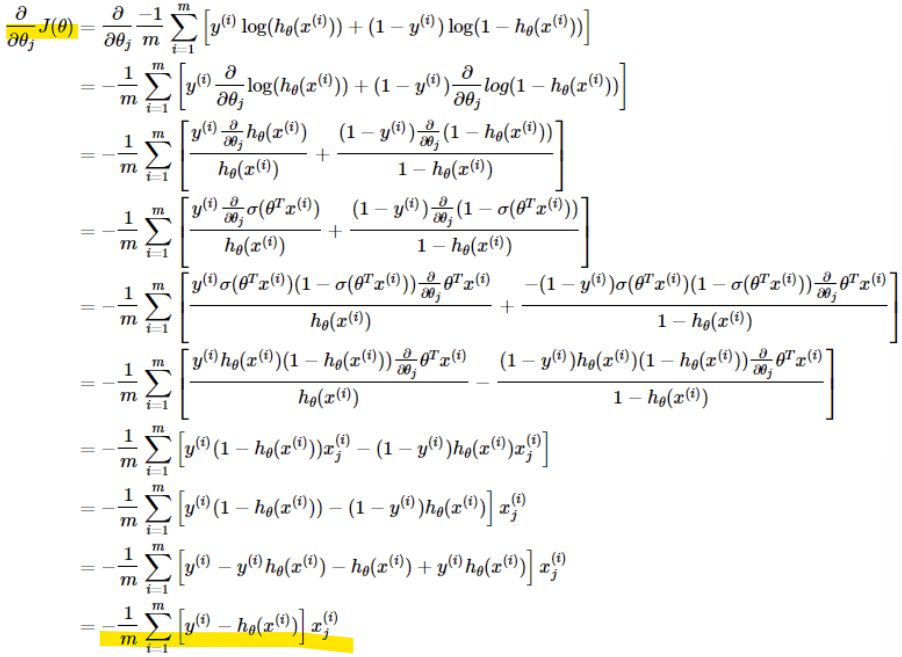
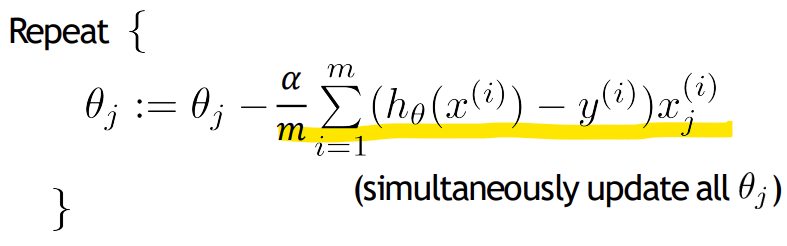
-> 미분한 J(theta) 대입
-> 알고리즘이 linear regression과 동일함
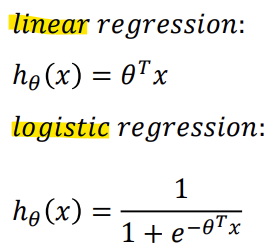


- Advanced optimization
- Optimization algorithms
- Gradient descent
- Conjugate gradient
- BFGS
- L-BFGS
<장점>
- 직접 learning rate값을 정할 필요 없음(수식에 learning rate가 없음)
- gradient descent보다 종종 빠름
<단점>
- 더 복잡함

-> optimset(): Matlab의 Optimization용 내장 함수
- Multi-class classification: One-vs-all
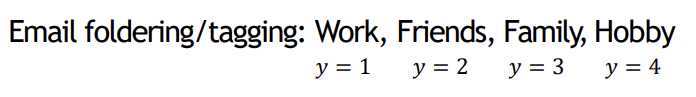
-> 여러 클래스로 나눠야 할 경우
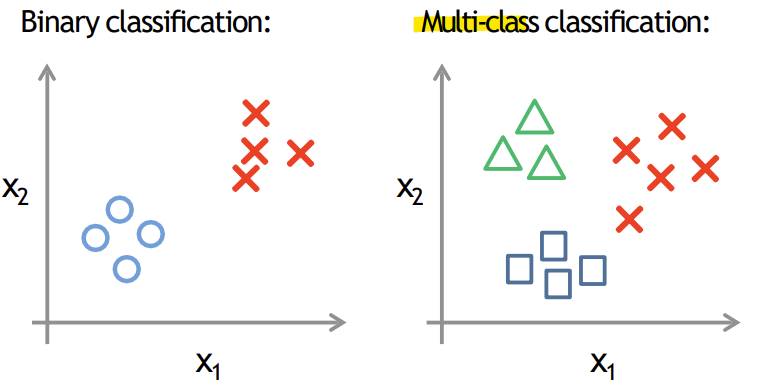
- One-vs-all(one-vs-rest)
: 각 클래스에 대해 개별 이진 분류기 학습함 (각 분류기는 해당 클래스 vs 나머지 클래스를 구분하도록 학습)
: 새로운 입력 x가 주어지면, 모든 분류기 hi(x)의 예측 확률을 계산함 -> 그 중 가장 높은 확률을 반환한 클래스 i를 최종 예측으로 선택함
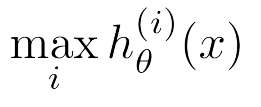
<장점>
- 간단함
<단점>
- class 개수만큼 classifier가 있어야 함
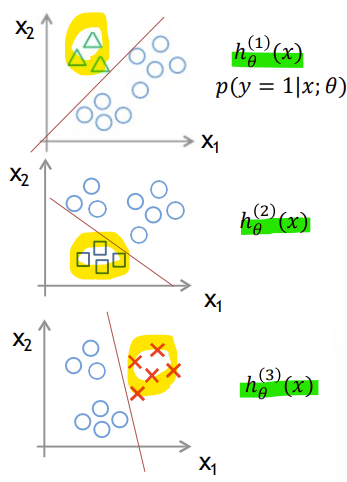
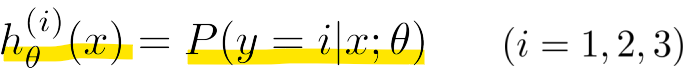
-> 각각의 h(1), h(2), h(3)의 확률을 계산하여 확률이 가장 높은 클래스에 속한다고 봄
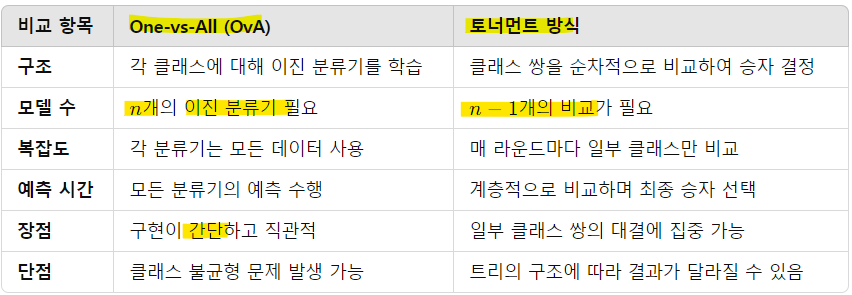
- Tournament-style Classification, 토너먼트 방식
: one-vs-all에 비해 class가 많아지면 좀 더 빠르게 결과가 나옴
: 그러나, 모든 combination을 학습시켜야함 (모델 크기가 커짐)