* Overfitting
: 너무 많은 features를 가지게 되면, 학습된 가설이 training set에서는 매우 잘 맞을 수 있지만, 새로운 예시들에 대해서는 일반화하지 못할 수 있음
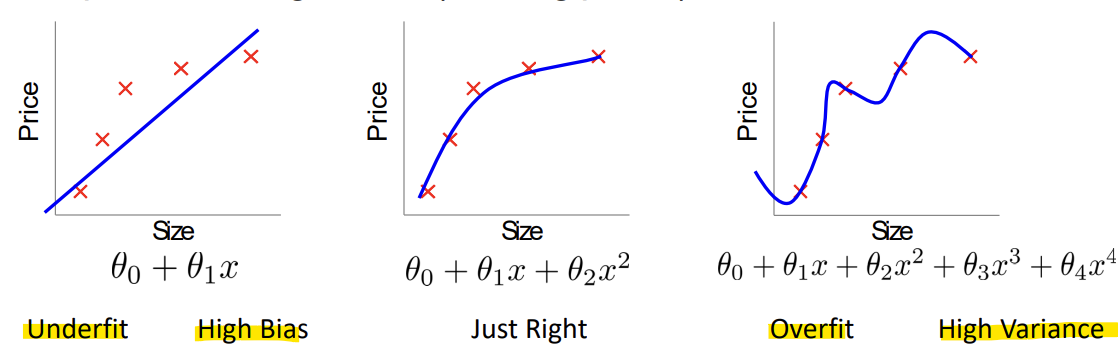
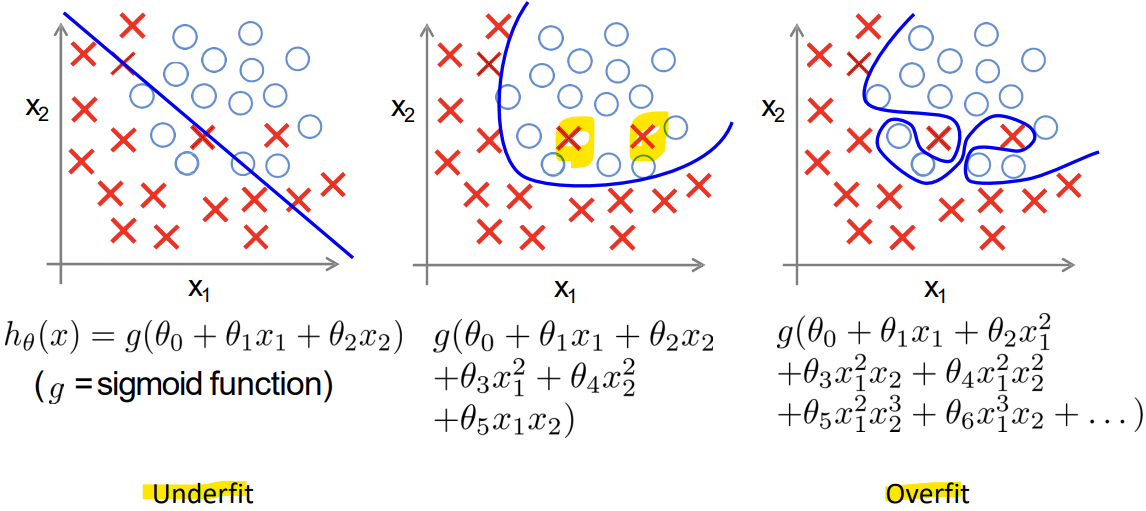
- Underfit (High Bias): 문제 복잡도보다 파라미터 수가 적음
- Overfit (High Variance): 문제 복잡도보다 파라미터 수가 너무 많음 -> Generality가 없음
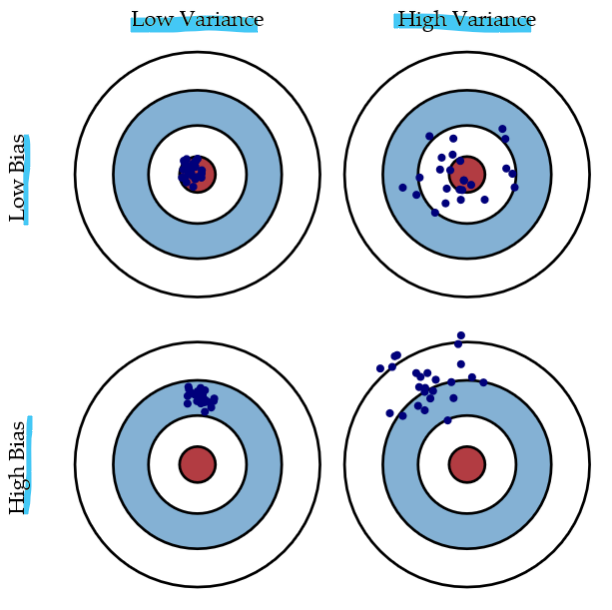
Bias ~ accuracy
Variance ~ precision- Bias (편향)
: 모델이 얼마나 단순하게 데이터의 패턴을 학습했는지를 나타냄- Variance (분산)
: 모델이 훈련 데이터의 세부적인 부분까지 지나치게 학습했는지를 나타냄
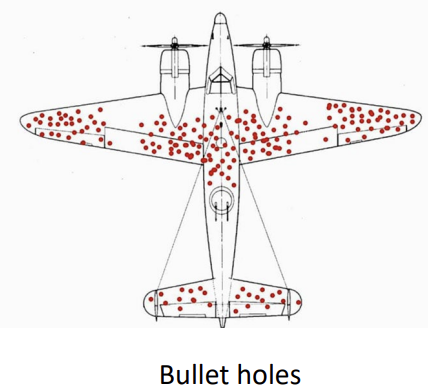
-> 살아돌아온 비행기가 공격당한 부분을 강화하는게 아닌, 공격당하지 않은 부분(중요한 부분이 공격당하지 않아서 살아돌아왔기 때문)을 강화해야 함
- Survivorship Bias(생존자 편향)
: 데이터에서 성공하거나 살아남은 대상만을 고려하는 오류
-> 실패 사례는 배제되기 때문에, 전체적인 관점을 왜곡할 수 있음
-> 사람이 data labeling을 하기 때문에, labeling 오류가 있을 수 있다는 것을 고려해야 함
< Addressing overfitting >
1) feature 수를 줄이기
- 직접 어떤 feature를 유지할지 선택해야 함 -> 잘못 선택할 가능성이 있음
- 모델 선택 알고리즘을 사용함
2) Regularization - 모든 feature를 유지하지만, 파라미터의 크기/값을 줄임
- 특징이 많고, 각각의 특징이 예측에 조금씩 기여하는 경우에 효과적
-> 2번이 더 좋음
- Regularization Cost function
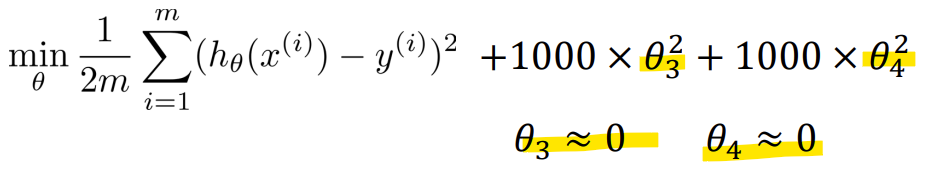
-> theta값을 0에 가깝게 만들면, 영향이 감소함
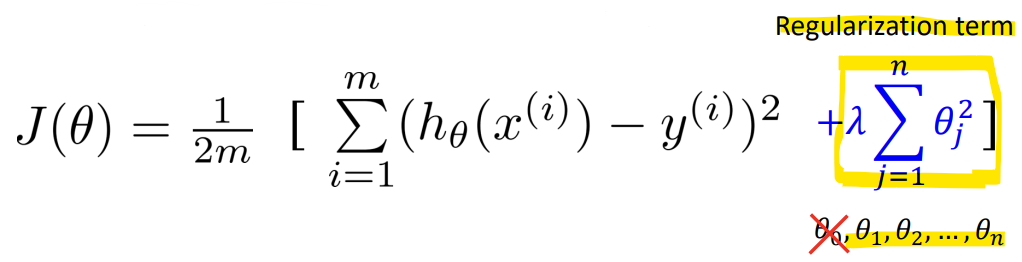
-> 손실함수 J(theta)에 Regularization term을 더해줌
-> 람다: Regularization parameter
-> theta0은 Bias term이므로 Regularization에서 제외!
<lambda 값의 크기 설정>
- lambda가 너무 작으면: Overfitting
- lambda가 너무 크면: Underfitting
- Regularized linear regression
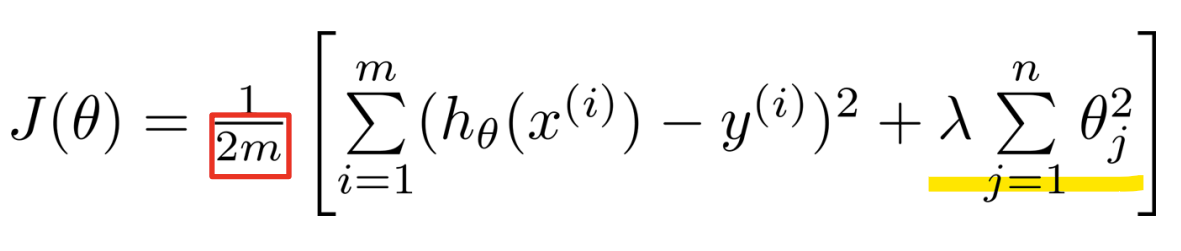
- Gradient descent(Regularized)
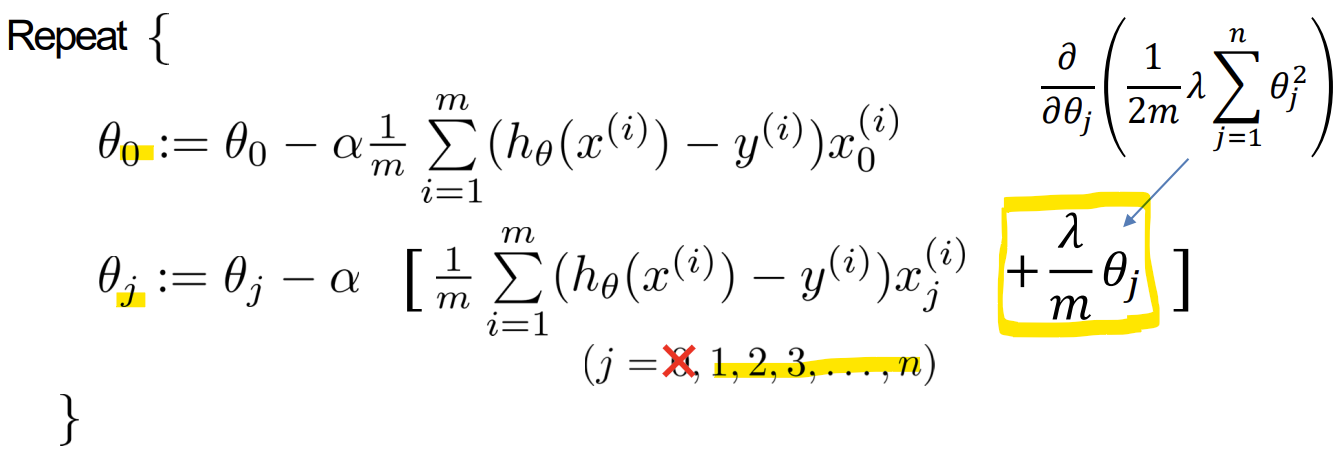
-> theta 0은 bias term이므로 theta 1부터 정규화 term 추가하여 업데이트 (범위 주의)

-> theta를 계속 업데이트하면, alpha * lambda / m가 항상 양수이므로 계속 theta가 줄어들게 됨
-> 1 - 양수 < 1
- Normal Equation(Regularized)
-
기존 Normal Equation
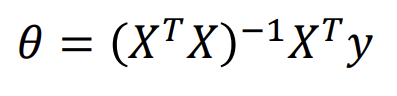
-
정규화된 Normal Equation
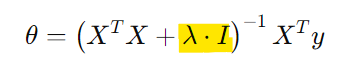
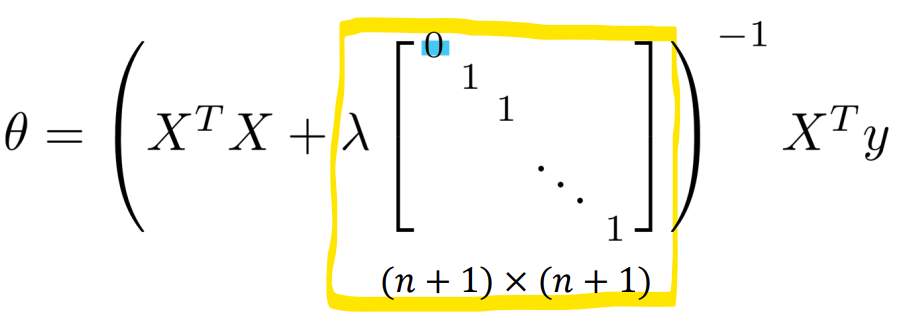
- Non-invertibility (optional/advanced)
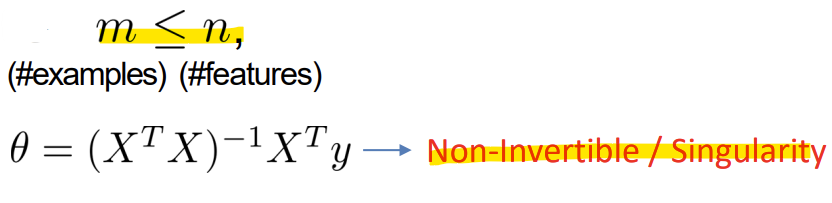
- m <= n 일 때 (샘플 수가 feature 수보다 적을 때), XT X는 역행렬 계산 불가함 (Non-Invertible)
-> 문제 해결을 위해 Regularization을 사용
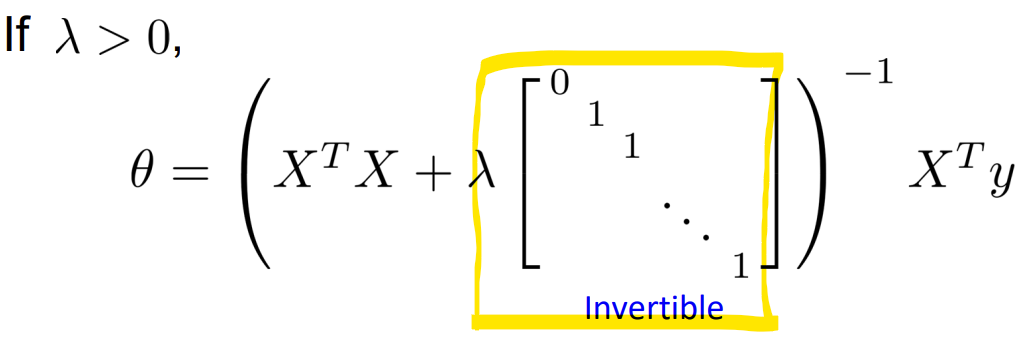
-> XT X에 lambda * I를 더하여 역행렬이 가능하게 만듦 (Invertible)
- Regularized logistic regression
-
Cost function
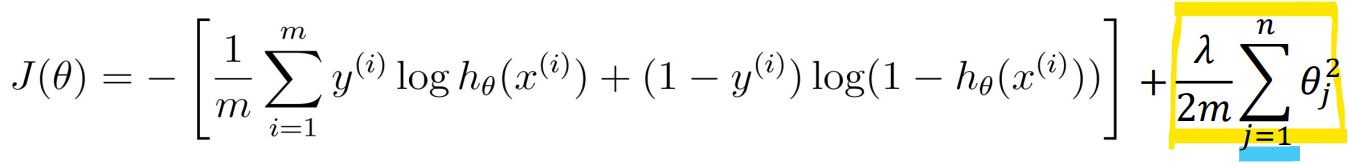
-> 정규화 항은 j = 1부터 시작 -
Gradient descent
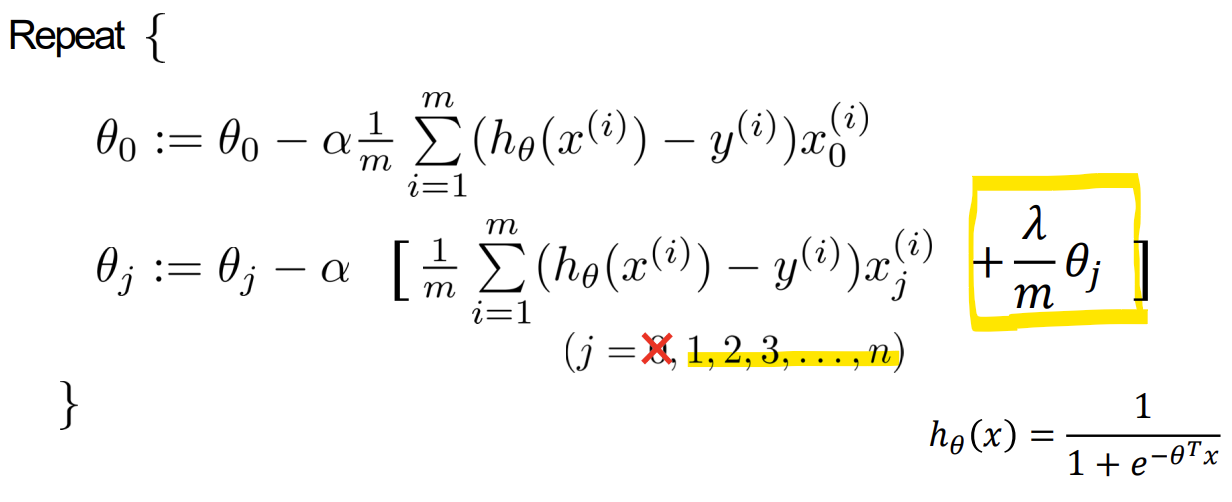
-> h(x)함수: Sigmoid

-> theta 0 은 bias term이라 정규화 안함 주의