Scientific Python 2

Scipy

• Scipy is a collection of packages that provide useful mathematical functions commonly used for scientific computing.

List of subpackages

• interpolate : Interpolation and smoothing splines
  → 보간법: 몇 개의 샘플 포인트들로 추정하여 인접한 점들 사이를 다항식 함수로 이어준 것에서 미싱포인트(추정)들을 계산/추정하는 방법이다.
  - interp.interp1d vs. interp.interp2d: 입력 데이터 차원이 다르고 서로 다른 보간 방식을 지원함(interp2d는 바이리니얼(bi-linear) 보간 방법을 사용)
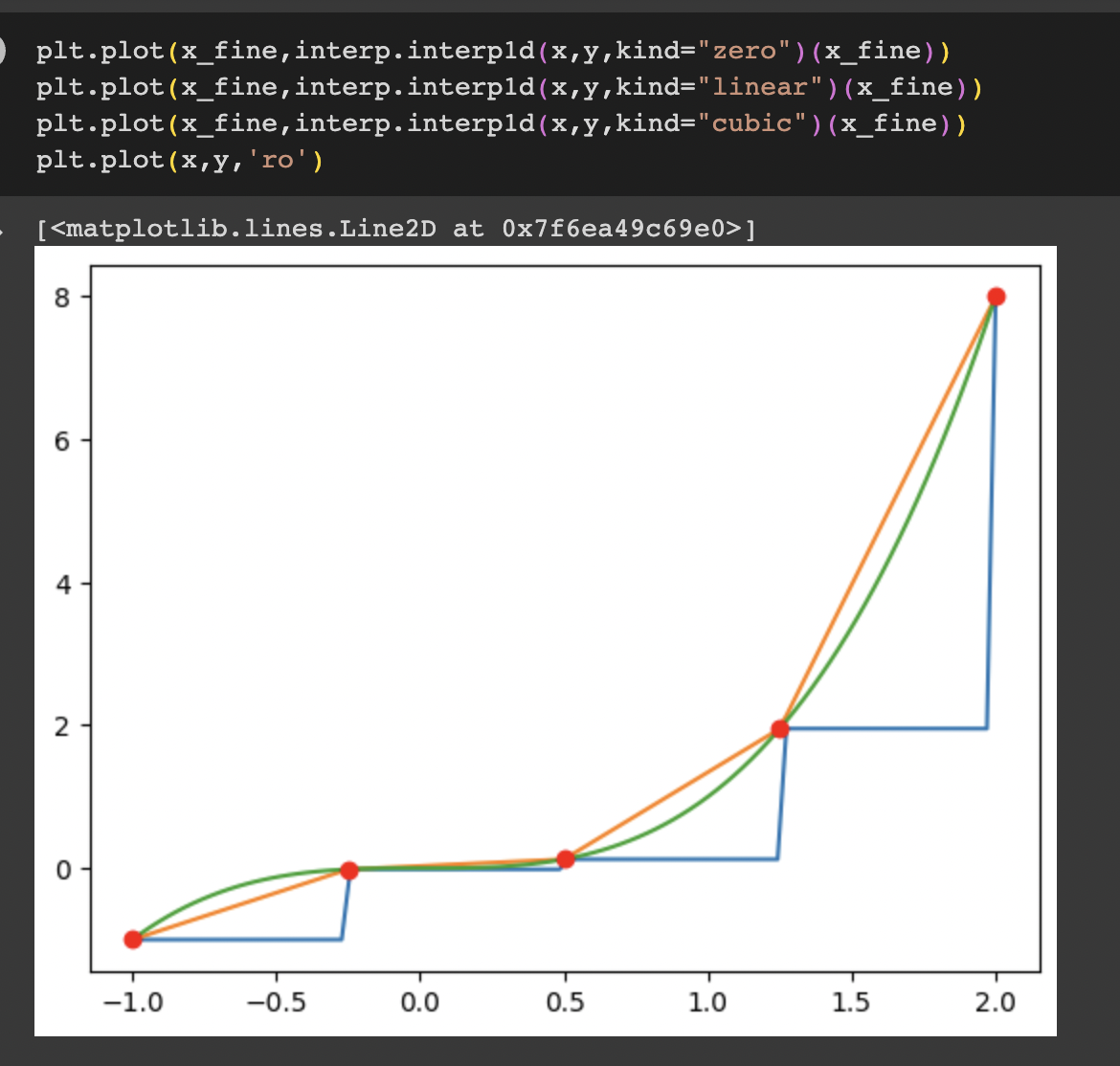
  - interp1d의 kind 옵션: 보간법을 선택할때 사용
  1) linear: 선형보정 → 데이터를 직선으로 연결
  2) nearest: 가장 가까운 이웃 값
  3) zero: 0차 다항식(0차 스플라인)
  4) slinear: 선형 스플라인(1차 다항식)
  5) quadratic: 2차 스프라인(다항식)
  6) cubic: 3차 스플라인(다항식)
  7) previous: 주어진 데이터 포인트 중 바로 앞의 값
  8) next: 주어진 데이터 포인트 중 바로 뒤의 값
  

• optimize : Optimization and root-finding routines
  → 다양한 최적화 알고리즘과 관련 도구를 제공하는 모듈: 그래디언트 계산, 자코비안 행렬 계산, Hessian 행렬 계산, 함수 값 캐싱 등 가능
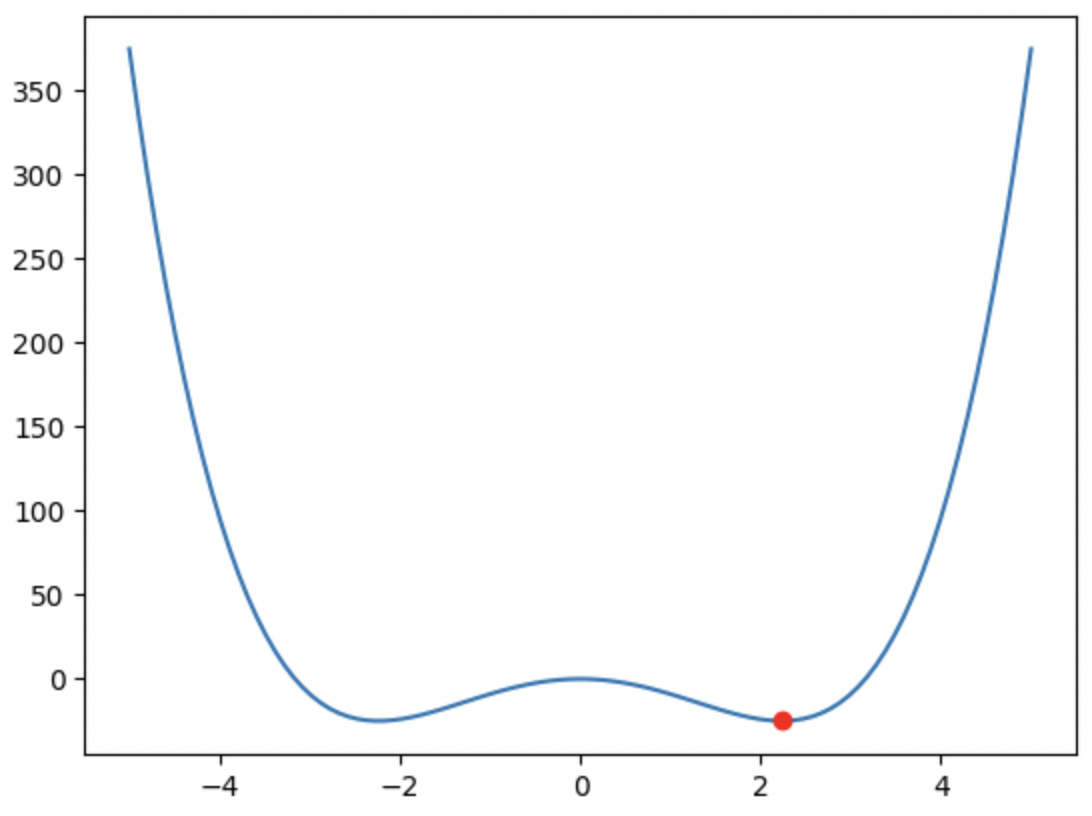
  1) minimize_scalar: 단일 변수 최적화
  2) minimize: 다변수 최적화 / constraint 변수를 사용해 제약 조건 최적화를 가능케 함
  3) basinhopping: 전역 최적화

  import matplotlib.pyplot as plt
  
  def f(x):
      return x**4 -10*x**2
  
  plt.plot(x,f(x));
  plt.plot(x_opt,f(x_opt),'ro');

  위와 같은 코드를 돌리면 아래와 같이 다변수 최적화가 된다.
  
  - optimize.curve_fit(): 주어진 모델 함수와 데이터를 기반으로 파라미터 추정(parameter estimation)을 수행

  import matplotlib.pyplot as plt
  
  def f(x,a,b):
    return a*x +b
    
  x_fine = np.linspace(-2,2,200)
  plt.plot(x_fine,f(x_fine,a,b))
  plt.plot(x,y,'ro')
  
  def g(x,a,b):
      return a*x +b*np.sin(6.5*x)
  
  x_fine = np.linspace(-2,2,200)
  plt.plot(x_fine,g(x_fine,a,b))
  plt.plot(x,y,'ro')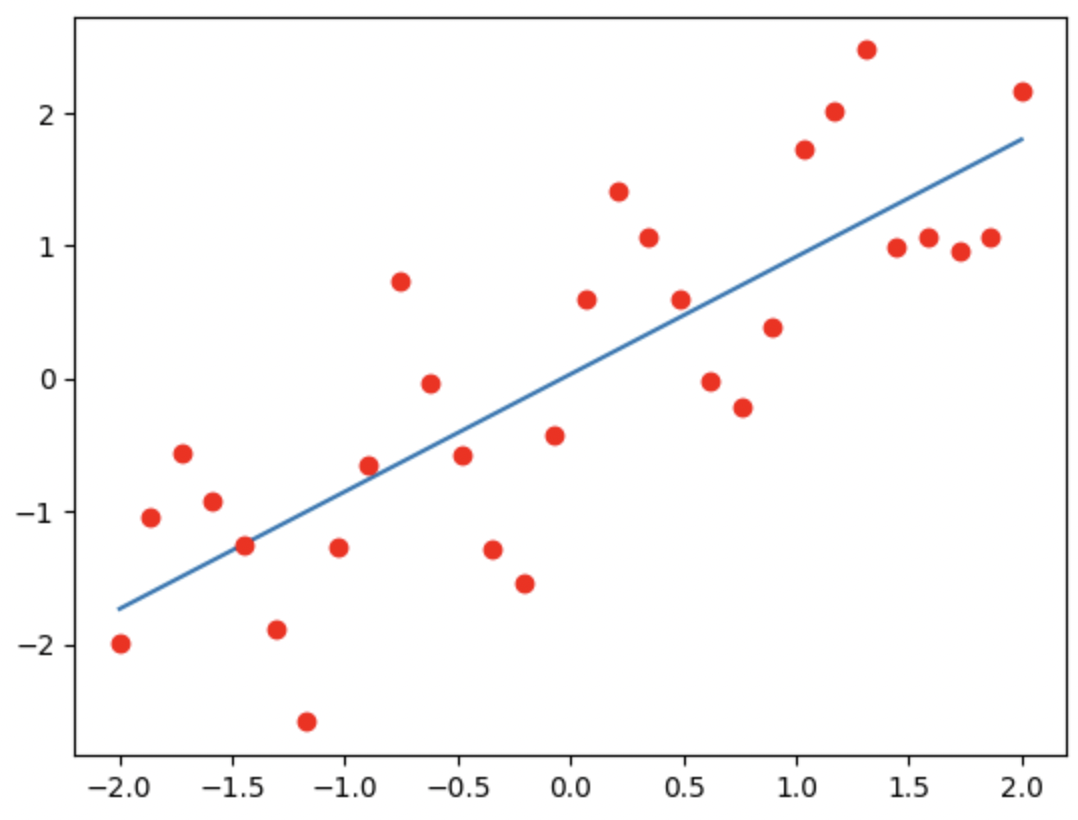

  
  
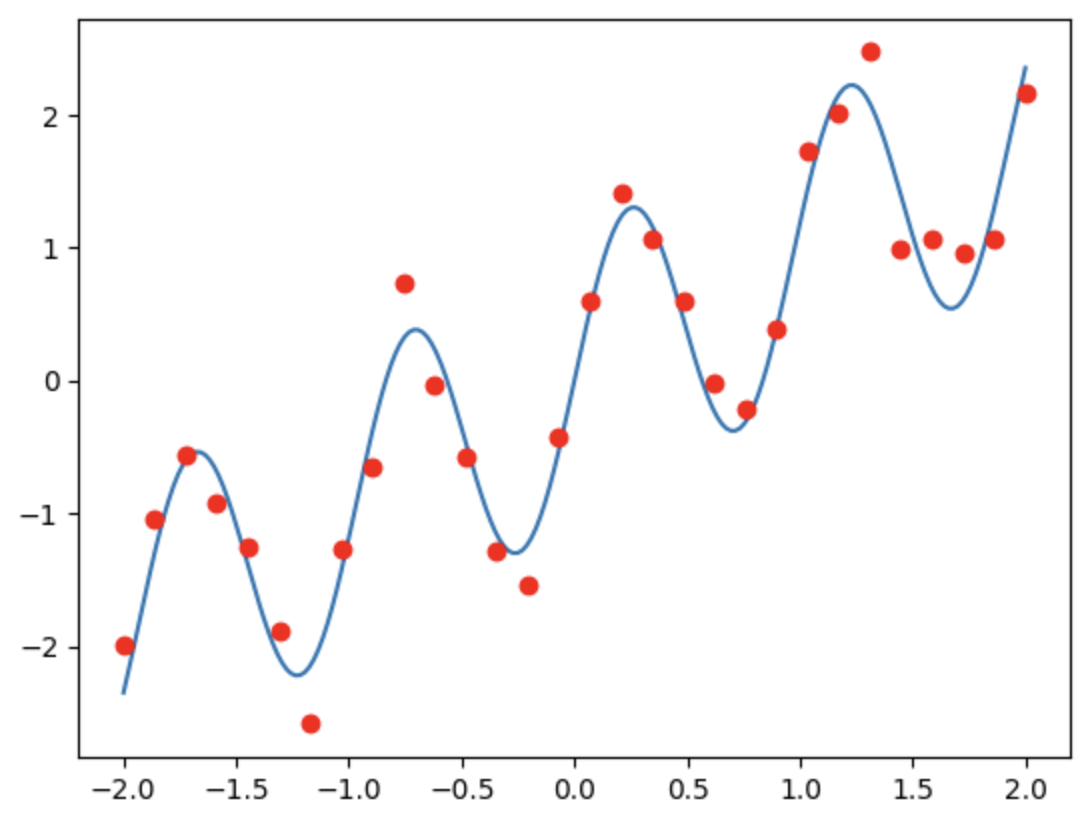
  순서대로 출력 값을 정리하였는데, 함수에 따라 추정이 달라짐을 알 수 있다.

• stats : Statistical distributions
  → 다양한 확률 분포와 통계적 함수를 제공
  - stats.kde.gaussian_kde(): 커널 밀도 추정(Kernel Density Estimation, KDE)을 수행하는 기능을 제공

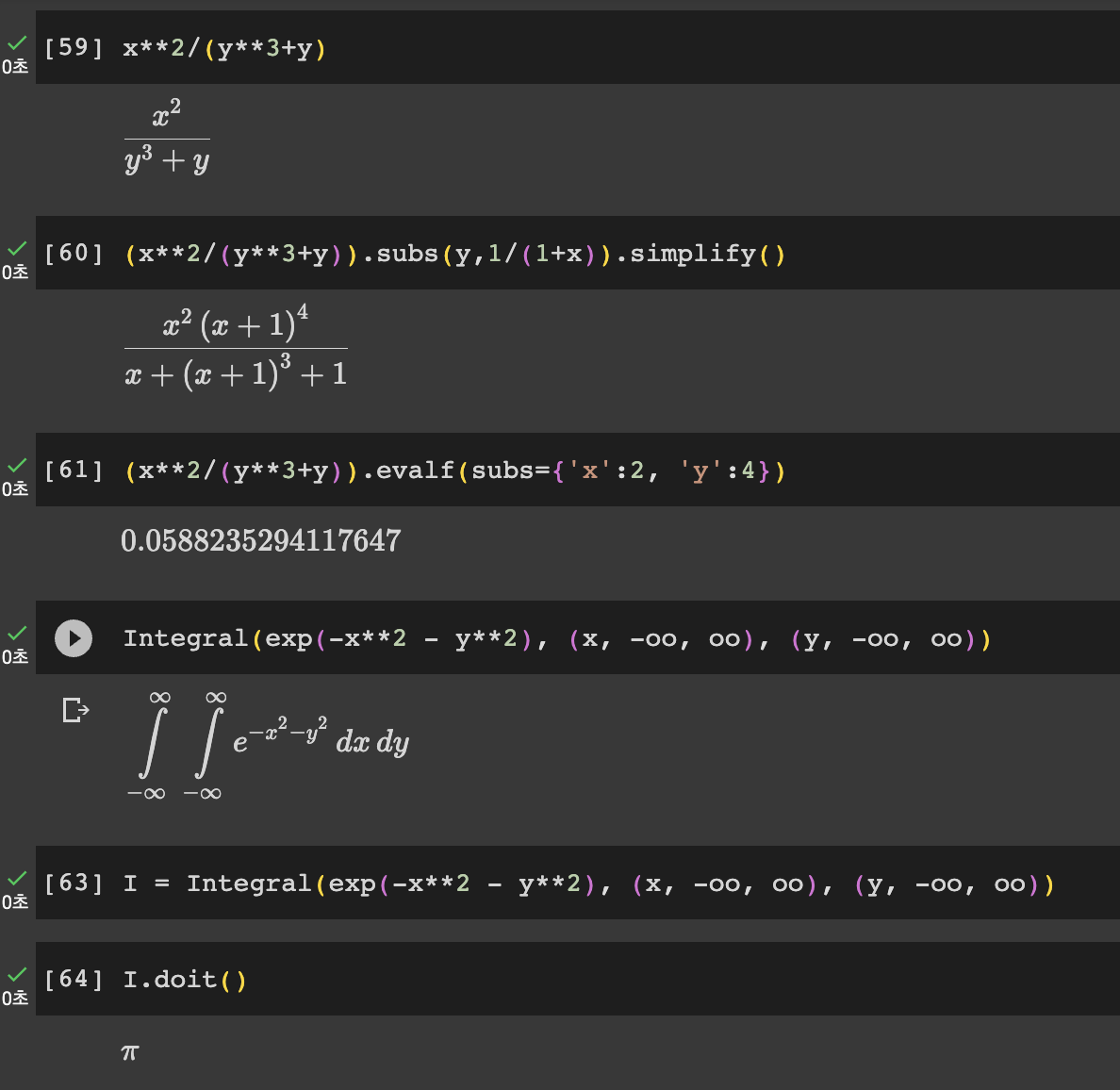
• integrate : Integration and ordinary differential equation solvers
  → 수치적 적분(numerical integration)을 수행하는 함수와 도구를 제공
  - quad: 단일 변수 정적분
  - dblquad: 다변수 정적분
  - quadpack: 수치 적분 도구
  - odein: 미분방정식 초기값 문제를 수치적으로 해결하는 함수
  - fft/ifft: 푸리에 변환과 역변환을 수행하는 함수

• networkx: 그래프와 네트워크를 구축하고 분석하기 위한 강력한 라이브러리
  - 노드와 엣지를 추가하여 유향 그래프, 무향 그래프, 가중치 그래프 등 다양한 유형의 그래프를 생성하고 조작할 수 있다.
  - 네트워크 구조를 분석하고 특성을 추출하는데 유용
  - 시각화 기능 제공

import networkx as nx

G = nx.Graph()
G.add_nodes_from([1,2,3,4])
G.add_edge(1,2)
G.add_edge(2,3)
G.add_edge(3,1)
G.add_edge(3,4)

G = nx.complete_graph(10)
nx.draw(G)

• sympy: 심볼릭 수학 라이브러리(파이썬으로 수식을 표현하고 조작할 수 있다.)
  

Pandas

for idx,val in s.iteritems(): #python3에서는 .items() 사용
    print(idx,val)

'''
결과값:
a -0.8467049357276993
b 0.7257672552631623
c 0.3685608531494231
d -0.8934624479869832
e 12.0
'''

• iteritems(): 딕셔너리의 키-값 쌍을 반복적으로 반환하는 반복자(iterator)를 생성

s = pd.Series([0,0,0,1,1,1,2,2,2,2])
sct = s.value_counts() # what is the type of sct?
print(sct)
type(sct)

'''
결과값:
2    4
0    3
1    3
dtype: int64
pandas.core.series.Series
'''

• value_counts(): 빈도수 체크 → 내림차순으로 정렬된 시리즈 반환
• Series.mode(): 시리즈 객체의 최빈값(mode)을 계산하는 함수
• Series.nsmallest(num): 시리즈에서 가장 작은 값을 반환하는 함수

# Create a dictionary of series
d = {'one': pd.Series([1,2,3], index  = ['a', 'b', 'c']), 
     'two': pd.Series(list(range(4)), index = ['a','b', 'c', 'd'])}
df = pd.DataFrame(d)
print(df, end = end_string)
'''
   one  two
a  1.0    0
b  2.0    1
c  3.0    2
d  NaN    3
'''

d= {'one': {'a': 1, 'b': 2, 'c':3}, 
     'two': pd.Series(list(range(4)), index = ['a','b', 'c', 'd'])}
# Columns are dictionary keys, indices and values obtained from series
df = pd.DataFrame(d)
# Notice how it fills the column one with NaN for d
print(df, end = end_string)
'''
one  two
a  1.0    0
b  2.0    1
c  3.0    2
d  NaN    3
'''

d = {'one': pd.Series([1,2,3], index  = ['a', 'b', 'c']), 
     'two': pd.Series(list(range(4)), index = ['a','b', 'c', 'd'])}

print(pd.DataFrame(d, index = ['d', 'b', 'a']), end = end_string)
print(pd.DataFrame(d, index = ['d', 'b', 'a'], columns = ['two', 'three']),
      end = end_string)
'''
one  two
d  NaN    3
b  2.0    1
a  1.0    0
-------------
   two three
d    3   NaN
b    1   NaN
a    0   NaN
'''

• 비어있는 부분은 NaN으로 처리하여 출력해준다. 열이 없어도 NaN으로 채워서 출력해준다.

pd.date_range('1/1/2000', periods=8)

• 2000년 1월 1일부터 8개의 기간(periods)을 포함하는 날짜 범위를 생성

Scikit Learn

X = df[['weight']].to_numpy() #2차원 리스트
y = df['rings'].to_numpy()

from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)
print(model.coef_, model.intercept_)
''' 출력
[3.55290921] 6.989238807755703
'''

print(model.score(X, y))
''' 출력
0.29202100292591804
'''

• 입력 변수(X)는 보통 2차원 배열 형태로 표현되는 데이터: 각 행은 개별 샘플을 나타내며, 각 열은 해당 샘플의 특성값을 나타낸다.
• model.score(): 회귀 모델의 경우 결정 계수(coefficient of determination)로 계산 → 데이터가 얼마나 적합한지 확인

for name in iris.target_names:
    plt.scatter(X[y == name, 0], X[y == name, 1], label=name)

• X[y == name, 0]은 첫 번째 특성인 꽃받침 길이(Sepal Length)를 나타내며, X[y == name, 1]은 두 번째 특성인 꽃받침 너비(Sepal Width)를 나타낸다.
• 5폴드 교차검증: 데이터셋을 5개의 폴드로 나누고, 각각의 폴드를 테스트 세트로 사용하고 나머지 폴드를 훈련 세트로 사용하여 모델을 학습하고 평가하는 방법
  → 폴드 중 하나를 테스트 셋으로 선정, 나머지는 훈련 세트

Dimensionality reduction

• 주성분 분석(Principal Component Analysis, PCA): PCA는 데이터의 분산을 최대로 보존하는 주요한 축을 찾아서 차원을 축소한다.
  

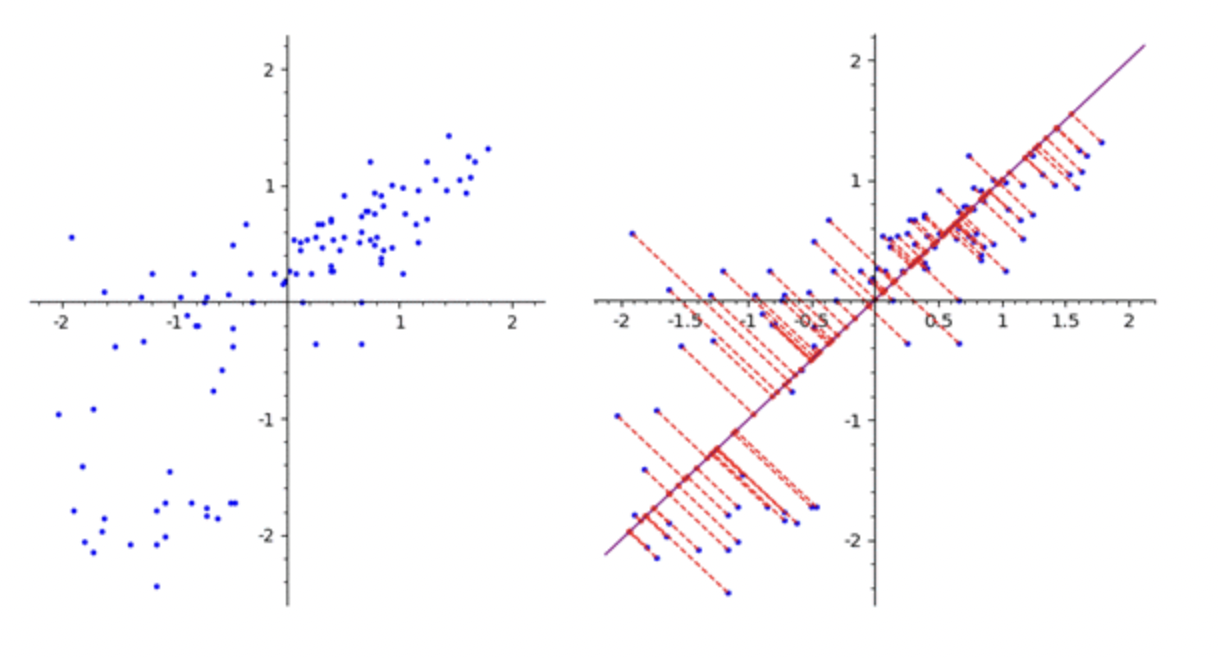
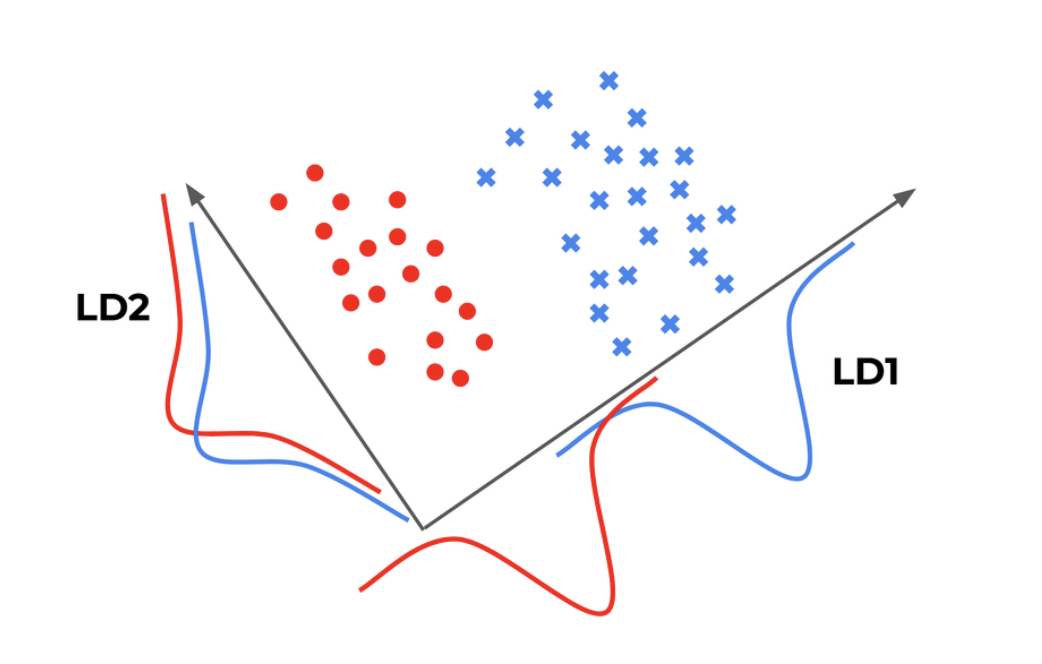
• 선형 판별 분석(Linear Discriminant Analysis, LDA): LDA는 지도학습에서 차원 축소를 수행하는 방법으로 클래스 간 분산과 클래스 내 분산의 비율을 최대화하는 축을 찾아서 데이터를 변환한다.
  → 데이터를 특정 한 축에 사영(projection)한 후에 두 범주(빨간색, 파란색)을 잘 구분할 수 있는 직선을 찾는 것이 목표
  

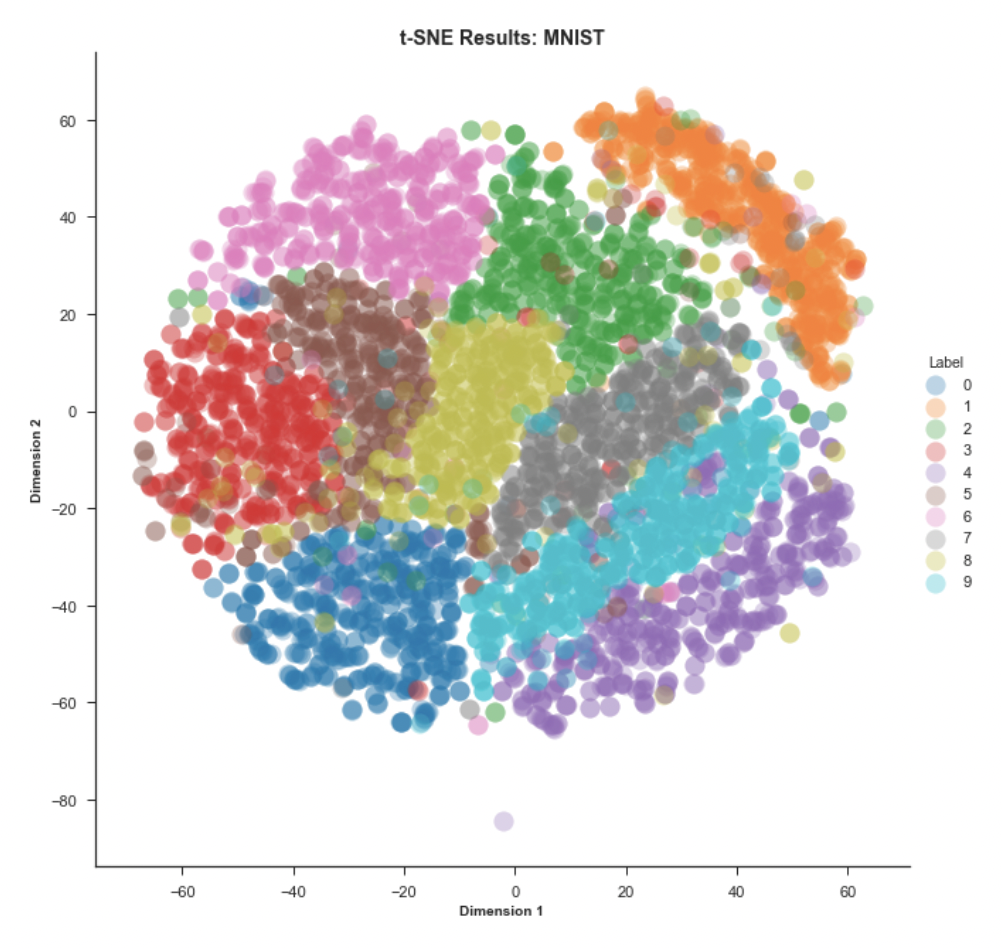
• t-SNE(t-Distributed Stochastic Neighbor Embedding): t-SNE는 고차원 데이터의 시각화를 위해 사용되는 비선형 차원 축소 알고리즘이다.
  

• 특이값 분해(Singular Value Decomposition, SVD): SVD는 행렬을 저차원의 근사 행렬로 분해하는 기법으로 행렬 분해를 통해 주요한 특성을 추출한다.
  → 특이값 분해는 정방 행렬뿐만 아니라 행과 열의 크기가 다른 행렬에 대해서도 적용
  
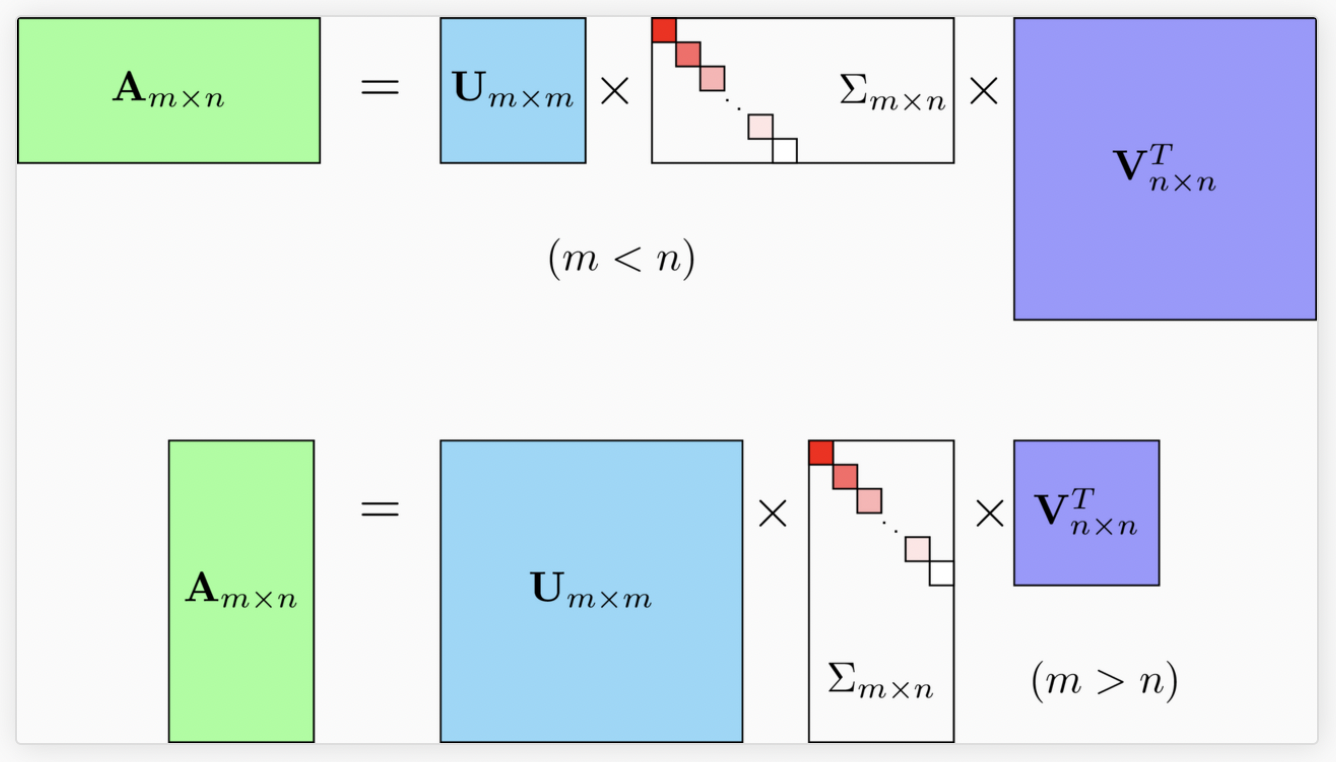
  - 행렬 U와 V에 속한 벡터를 특이 벡터(Singular Vector)라 한다. 모든 특이 벡터는 서로 직교한다.
  - ∑는 직사각 대각 행렬이며, 행렬의 대각에 위치한 값만 0이 아니고 나머지 위치의 값은 모두 0이다. ∑의 0이 아닌 대각 원소값을 특이값(Singular Value)이라고 한다.
  - U와 V에 속한 열 벡터를 특이 벡터(Singular Vector)라 한다. U에 속한 벡터를 Left Singular Vector, V에 속한 벡터를 Right Singular Vector라고 한다.

  → 선형 변환 A 후에도 그 크기는 ∑만큼 변하지만 여전히 직교하는 벡터를 만든다.

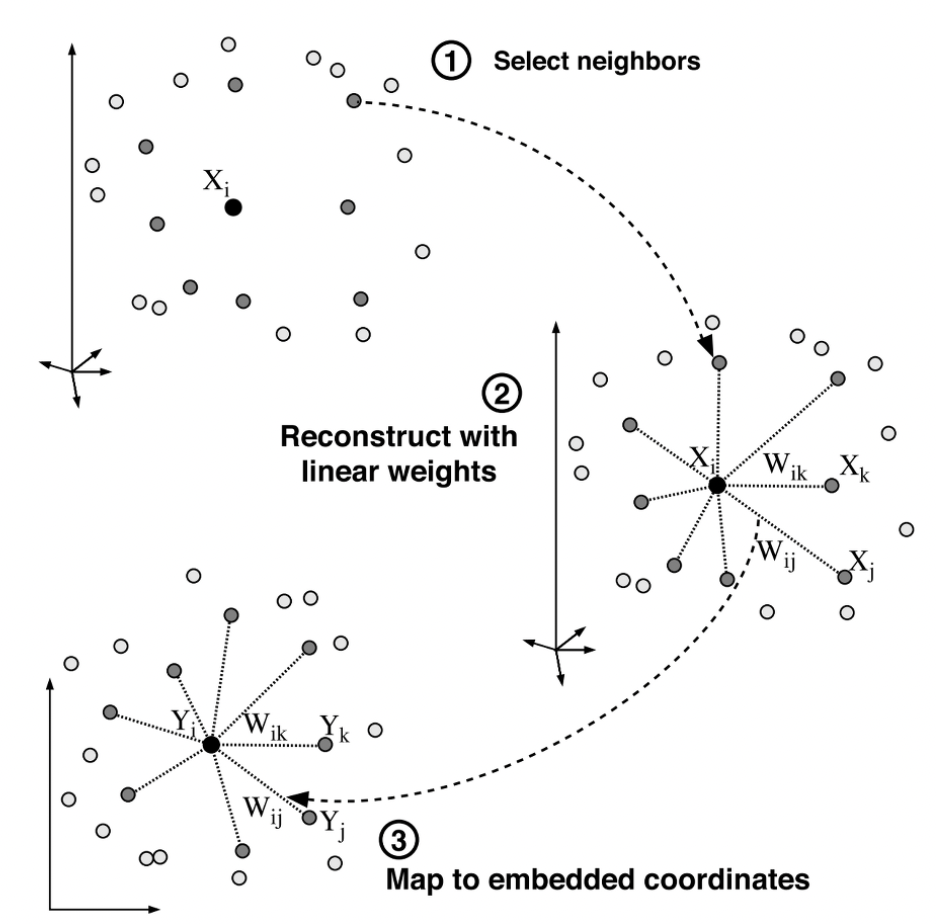
• LLE(Locally Linear Embedding): LLE는 비선형 차원 축소 알고리즘으로, 지역적으로 선형인 패턴을 보존하는 방식으로 데이터를 저차원으로 매핑한다.
  → 거리를 추정할 필요가 없고, 국소적인 선형 적합으로 부터 전역적인 비선형 구조를 복원한다.

  (1단계) 각 데이터 점의 이웃을 선택 (Select neighbors)
  (2단계) 이웃으로부터 선형적으로 가장 잘 재구성하는 가중치를 계산 (Reconstruct with linear weights)
  (3단계) 가중치를 사용해 저차원의 임베딩 좌표로 매핑 (Map to embedded coordinates)
  

Pytorch

A_gpu = A.to(gpu) #데이터를 GPU로 보냄: 데이터를 GPU로 복사
B_gpu = B.to(gpu)

A_gpu@B_gpu
'''출력
tensor([[22.1136, 23.1953, 23.0761,  ..., 22.0609, 22.9691, 22.4580],
        [22.3957, 22.2071, 23.4089,  ..., 22.1435, 23.8955, 24.0480],
        [25.7805, 23.3261, 24.7989,  ..., 22.4402, 25.1166, 24.7828],
        ...,
        [21.5669, 22.1809, 21.5585,  ..., 22.0518, 23.5019, 23.3384],
        [26.2310, 27.7557, 26.9037,  ..., 25.7191, 25.0999, 26.4186],
        [26.2045, 26.5745, 25.8596,  ..., 24.5887, 22.8976, 25.9937]],
       device='cuda:0')
'''

A@B_gpu
'''출력
---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
<ipython-input-7-c90cee74ed92> in <cell line: 1>()
----> 1 A@B_gpu

RuntimeError: Expected all tensors to be on the same device, but found at least two devices, cpu and cuda:0! (when checking argument for argument mat2 in method wrapper_CUDA_mm)
'''

• 데이터를 GPU로 이동하는 이유는 GPU의 병렬 처리 능력을 활용하여 연산을 가속화하기 위함이다.
• GPU끼리만 @연산 가능

x = torch.tensor([2.0])
m = torch.tensor([5.0], requires_grad = True)
c = torch.tensor([2.0], requires_grad = True)

y = m*x + c

loss = torch.norm( y - 13)

loss.backward()

• 임의의 텐서에서 x.backward()를 호출하면 pytorch가 requires_grad 플래그가 True로 설정된 x를 계산하는 데 사용되는 텐서의 모든 그레이디언트를 계산한다. 계산된 기울기는 텐서의 .grad 속성에 저장된다.

Neural Network Intro

• Activation function

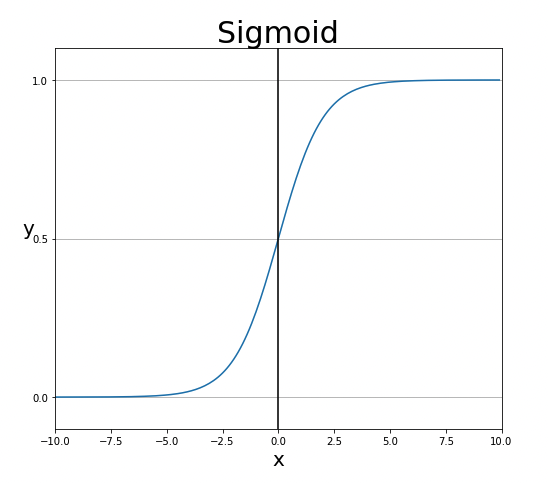
  1) 시그모이드 함수(Sigmoid function): 시그모이드 함수는 실수 입력을 0과 1 사이의 값으로 압축하는 S자 모양의 함수이며 주로 이진 분류 문제에서 사용된다.
  → torch.sigmoid()로 구현가능
  

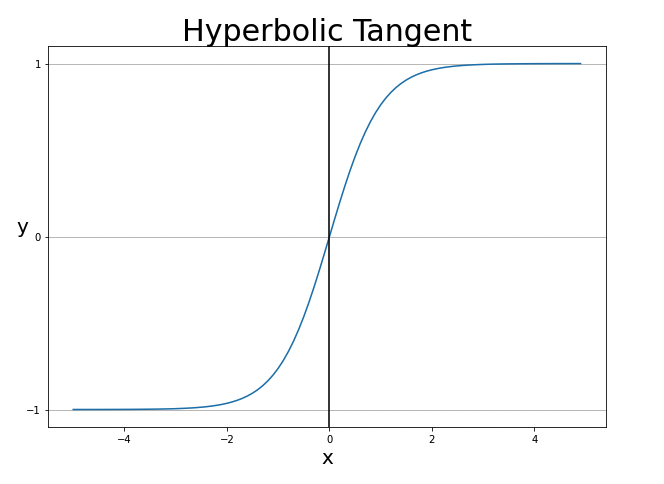
2) 하이퍼볼릭 탄젠트 함수(Hyperbolic tangent function): 하이퍼볼릭 탄젠트 함수는 실수 입력을 -1과 1 사이의 값으로 압축하는 함수이며 다양한 종류의 신경망에서 사용된다.
→ torch.tanh()로 구현가능

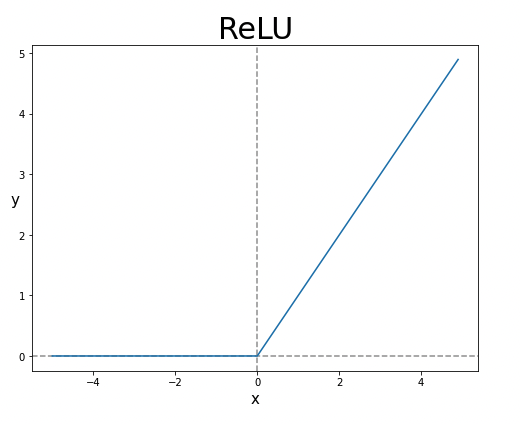
3) ReLU 함수(Rectified Linear Unit, ReLU): ReLU 함수는 음수 입력을 0으로 변환하고 양수 입력은 그대로 유지하는 함수로 주로 은닉층에서 사용되며, 비선형성을 추가하면서도 연산이 간단하고 계산량이 작기 때문에 많이 쓰인다.
→ torch.relu()로 구현가능

4) 소프트맥스 함수(Softmax function): 소프트맥스 함수는 주로 다중 클래스 분류 문제에서 사용되며, 각 클래스에 대한 확률 분포를 출력하기 위해 사용된다. 소프트맥스 함수는 입력 벡터의 각 요소를 양수로 변환하고, 합이 1이 되도록 정규화한다.
→ torch.softmax()로 구현가능