[머신러닝] ✨모델 (회귀 vs 분류)✨

✏️ 회귀 (Regression)

• 임의의 수치(연속적인 값)를 예측하는 문제
• score 확인시, "결정 계수(R2)"로 평가
• 손실 함수 확인시, '평균 제곱 오차mean squared error'사용
• mean_absolute_error() : 회귀 모델에의 평균 절댓값 오차 계산

from sklearn.metrics import mean_absolute_error
test_prediction = knr.predict(test_input) #예측값
mae = mean_absolute_error(test_target,test_prediction) #test_target : 정답값, test_prediction : 예측값
print(mae)
>>
19.157142857142862
#예측이 타깃값과 19 정도 차이가 난다는 뜻

💡 K-최근접 이웃 회귀

• 사례 기반 학습
• 학습된 범위 이상 예측이 어려움
• 데이터 스케일링 필요할 수도 있음

from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()

💡 선형 회귀 (Linear Reg.)

from sklearn.linear_model import LinearRegression
lr = LinearRegression()

• 모델 기반 학습
• 특성 & 타깃간 관계를 가장 잘 나타내는 선형 방정식을 구함 (a=기울기, b= y절편)
  $y=ax×b$

# a & b 구하기
print(lr.coef_, lr.intercept_)

# a = lr.coef_ / 특성에 대한 계수를 포함한 배열 = 특성의 개수
# b = lr.intercept_ / 절편

• 선형 회귀가 찾은 특성 & 타깃 관계는 선형 방정식의 '계수' 혹은 '가중치'에 저장
• 잔차 (residue)
  • 에러 값
  • 어떤 모델이 데이터의 정보를 적절하게 잡아냈는지 여부를 확인할 때 유용
  • 잔차의 평균이 0인 정규 분포를 따라야 함
  • 잔차 평가 : 잔차의 평균이 0이고 정규분포를 따르는지 확인
• 2차방정식 (다항회귀/곡선형/비선형) : 혼공머신 139p 확인
  • get_feature_names_out()

    poly=PolynomialFeatures(include_bias=False)
    poly.fit(train_input)
    train_poly=poly.transform(train_input)
    poly.get_feature_names_out()
    #[19.6, 5.14 , 3.04 , 384.16, 100.744 , 59.584, 26.4196, 15.6256, 9.2416]의 값은
    #array(['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2','x2^2'], dtype=object)으로 계산됨

💡 다중 회귀

• 2개 이상의 여러 개의 특성을 사용한 선형 회귀
• 선형 회귀 모델과 동일한 from sklearn.linear_model사용
• 특성이 많 -> 선형 모델의 고성능 발휘

💡 릿지 & 라쏘 회귀

• 선형 회귀 모델에 규제regularzation를 추가한 모델
• 해서 선형 모델과 동일하게 from sklearn.linear_model사용
• 두 모델 모두 계수의 크기를 줄이지만 '라쏘'는 0까지 가능

1. 릿지 회귀

• 계수를 제곱한 값을 기준으로 규제 적용
• '릿지'를 '라쏘'보다 더 선호하는 추세

from sklearn.linear_model import Ridge
ridge=Ridge()
ridge.fit(train_X,train_y)

2. 라쏘 회귀

• 계수의 절대값을 기준으로 규제 적용

from sklearn.linear_model import Lasso
lasso=Lasso()
lasso.fit(train_X,train_y)

💡 회귀 result 확인하기

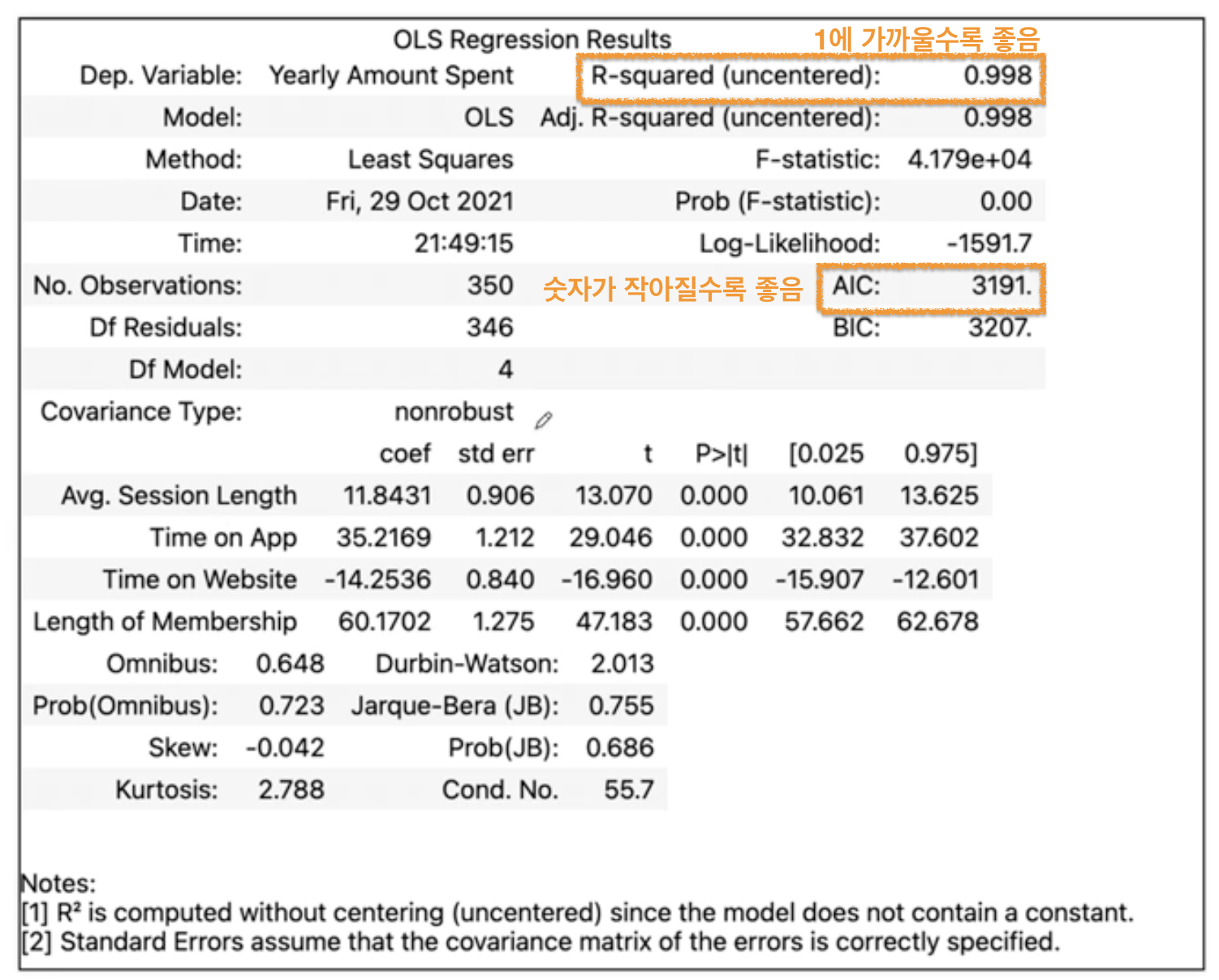
💡 비용함수 (Coste Func.)

[머신러닝] 비용함수(Cost Function)란

---

✏️ 분류(Classification)

특징

• 예측값으로 이산적인 값을 출력
  • 이산값 : 0과1로 처리할 수 있는 값으로써 연속적이 아닌 단속적인 값
  • 아이리스 문제, 와인 종류, 부도 여부(yes/no), 여신 승인 여부, 동물 분류(dog/cat) 등
• 종류 (혼공머신 - 190p, 356p)
  • 이진 분류 : Yes/ No처럼 두가지의 답으로 분류하는 것
  • 다중 분류 : 다양한 답으로 분류 (타깃 데이터에 클래스가 2개 이상)

• 이진 분류 (딥러닝 관련)

함수 종류	설명
활성화 함수	'시그모이드 함수' 사용 (하나의 선형 방정식 출력값을 0~1사이로 압축)
손실 함수	- '로지스틱 손실 함수' 혹은 '이진 크로스 엔트로피 손실 함수' 사용 - binary_crossentropy

• 다중 분류 (딥러닝 관련)

함수 종류	설명
활성화 함수	'소프트맥스 함수' 사용 (여러 개의 선형 방정식의 출력값을 0 ~ 1사이로 압축 & 전체 합을 1로)
손실 함수	- '크로스 엔트로피 손실 함수' 사용 - categorical_crossentropy - 원-핫 인코딩이 준비되어 있지 않을 경우, sparse_categorical_crossentropy

손실 함수 (비용 함수)
  - 지도학습(Supervised Learning) 시, 알고리즘이 예측한 값과 실제 정답의 차이를 비교하기 위한 함수.
  - '학습 중에 알고리즘이 얼마나 잘못 예측하는 정도'를 확인하기 위한 함수로써 최적화(Optimization)를 위해 최소화하는 것이 목적인 함수 

다중 분류

• 다중 분류 : 다양한 답으로 분류 (타깃 데이터에 클래스가 2개 이상)
  • 타깃을 1과0이 아닌 알파벳 그대로 사용 가능하나, 알파벳 순서로 정렬됨
  • 클래스 배열 확인하기

---

💡 K-최근접 이웃 알고리즘

• KNeighborsClassifier(n_neighbors=n)
• sklearn.neighbors.KNeighborsClassifier
• 사례 기반 학습
• 거리기반 분류분석 모델
  • 가장 가까운 유사 속성에 따라 분류하여 라벨링하는 것
  • 거리가 가까운 'k'개의 다른 데이터의 레이블을 참조하여 분류하는 알고리즘
  • 다수를 보고! 다수를 차지!하는 것을 정답으로 사용
  • 사전에 기준치(단위,스케일)를 맞춰야 함 => 특성공학 차원에서 표준 편차, 표준 점수를 이용 하는 편
  • 거리 측정시 '유클리드 거리' 계산법 사용
• 데이터가 아주 많은 경우 사용하기 어려움
• 데이터 스케일링이 필요할 수도 있음 `혹은 plt.axis('equal')로 x축, y축 동일하게 만들어서 산점도 확인해보기

from sklearn.neighbors import KNeighborsClassifier
kn=KNeighborsClassifier()
#train_y 는 다중 클래스
kn.fit(train_X, train_y)
kn.classes_

파라미터 (Parameters)	설명
n_neighbors	- n_neighbors=int (참고할 데이터 개수,default=5) ex) kn49=KenighborsClassifier(n_neighbors=49) 가장 가까운 49개 데이터에서 다반수인 것을 예측 - 분류가 가능하도록 K는 홀수로 설정하는 것이 좋으며, 일반적으로는 총 데이터 수의 제곱근 값을 사용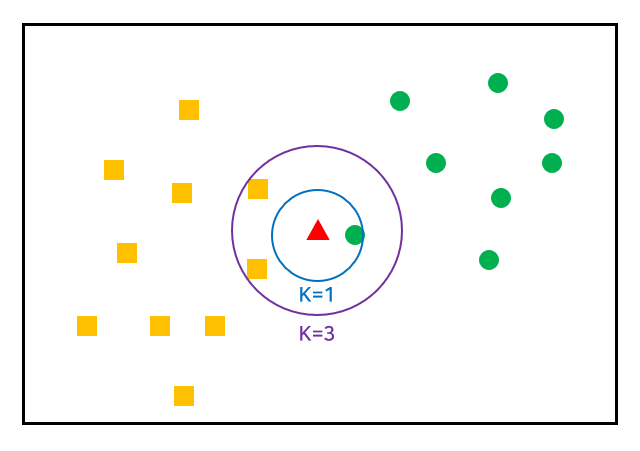
weights	- {‘uniform’, ‘distance’}, callable or None, default=’uniform’
algorithm	- {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’
n_jobs	- n_neighbors=int (default=None)

print(kn._fit_X) #knn으로 훈련된 x 프린트
print((kn._y) #knn으로 훈련된 x 프린트

- 가장 가까운 이웃 값들 구하기 (이웃 개수 : 기본값 5일 때)

distance, indexes= kn.kneighbors([[25,150]])

train_input[indexes]
>>>
array([[[ 25.4, 242. ],
        [ 15. ,  19.9],
        [ 14.3,  19.7],
        [ 13. ,  12.2],
        [ 12.2,  12.2]]])

💡 ⭐️로지스틱 회귀

• 이진 분류 & 다중 분류에 사용되므로 '분류'파트에 작성
• 선형 회귀와 같이 '선형 방정식' 사용하지만 값을 0~1사이로 압축 ('타깃'일 확률을 계산함)
  • 다중 분류-원 핫 인코딩 : 타깃 값 클래스만 1, 나머지 0인 배열로 만드는 것
• 선형 회귀와 달리 '시그모이드 함수', '소프트맥스 함수' 사용

from sklearn.linear_model import LogisticRegression
lr= LogisticRegression()

💡 ⭐️SGD Classifier (확률적 경사 하강법)

• 머신러닝, 특히 딥러닝에서 사용되는 가장 대표적인 최적화 알고리즘
• 한 번에 하나 또는 일부의 훈련 샘플을 사용하여 그라디언트를 계산하고 매개 변수를 업데이트
• 수렴 속도가 느리고, 최적화 문제에 따라 최솟값을 찾는 데 어려움이 있을 수 있음
• 2차원 배열 X, 1차원 배열 O
  train_X= train_X.reshape(-1,n)
train_X= train_X.reshape(1,n)

from sklearn.linear_model import SGDClassifier
sc=SGDClassifier(loss='log_loss',max_iter=10,random_state=42)
#loss='log_loss' : 로지스틱 손실 함수 -> 클래스가 많아도 이진 분류 모델 생성 (a=양성, 나머지는 다 음성)
#loss 기본값 : hinge
#max_iter=10 : 10번 반복
sc.fit(train_X train_y)

이어서 모델 수행하기

sc.score(train_X, train_y)

에포크 300번 반복

# _ : 임시로 두는 것, 그냥 버리는 값
for _ in range(0,300):
    sc.partial_fit(train_X, train_y, classes=classes)
    train_score.append(sc.score(train_X,train_y))
    test_score.append(sc.score(test_X, test_y))

---

✏️ 출처

제로베이스 '데이터 취업스쿨' 수강중
교재 '혼자 공부하는 머신러닝 + 딥러닝'
머신러닝 - 회귀(Regression) VS 분류(Classification)
회귀문제와 분류문제(Regression & Classification)